Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T15:24:31.843Z Has data issue: false hasContentIssue false
  • English
  • Français

Hybrid bounds for automorphic forms on ellipsoids over number fields

Part of: Partial differential equations on manifolds; differential operators Algebraic number theory: global fields Forms and linear algebraic groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  20 December 2012

Valentin Blomer  and
Philippe Michel
Valentin Blomer
Affiliation:
Mathematisches Institut, Universität Göttingen, Bunsenstr. 3-5, 37073 Göttingen, Germany ([email protected])
Philippe Michel
Affiliation:
EPFL/SB/IMB/TAN, Station 8, CH-1015 Lausanne, Switzerland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove upper bounds for Hecke–Laplace eigenfunctions on certain Riemannian manifolds 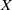$X$ of arithmetic type, uniformly in the eigenvalue and the volume of the manifold. The manifolds under consideration are 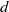$d$-fold products of 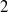$2$-spheres or 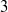$3$-spheres, realized as adelic quotients of quaternion algebras over totally real number fields. In the volume aspect we prove a (‘Weyl-type’) saving of 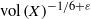$\mathrm{vol} \hspace{0.167em} (X)^{- 1/ 6+ \varepsilon } $.

Keywords

definite quaternion algebrastrace formulasup-normshybrid boundsnorm formsspherical harmonics

MSC classification

Secondary: 11R52: Quaternion and other division algebras 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F72: Spectral theory; Selberg trace formula 11E20: General ternary and quaternary quadratic forms; forms of more than two variables 58J50: Spectral problems; spectral geometry; scattering theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 4 , October 2013 , pp. 727 - 758
Copyright
©Cambridge University Press 2012 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blomer, V. and Holowinsky, R., Bounding sup-norms of cusp forms of large level, Invent. Math. 179 (3) (2010), 645–681.CrossRefGoogle Scholar
Blomer, V. and Michel, Ph., Sup-norm bounds for eigenfunctions on ellipsoids, Int. Math. Res. Not. 2011 (21) (2011), 4934–4966.Google Scholar
Cassels, J. W. S., Rational quadratic forms, London Mathematical Society Monographs, Volume 13 (Academic Press Inc. [Harcourt Brace Jovanovich Publishers], London, 1978).Google Scholar
Duke, W., Friedlander, J. and Iwaniec, H., Class group $L$-functions, Duke Math. J. 79 (1) (1995), 1–56.Google Scholar
Erdélyi, T., Magnus, A. P. and Nevai, P., Generalized Jacobi weights, Christoffel functions, and Jacobi polynomials, SIAM J. Math. Anal. 2 (1994), 602–614.Google Scholar
Faraut, J., Analysis on Lie groups. An introduction, Cambridge Studies in Advanced Mathematics, Volume 110 (Cambridge University Press, Cambridge, 2008).Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products, 7th ed. (Elsevier/Academic Press, Amsterdam, 2007).Google Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level. III, Math. Ann., in press.Google Scholar
Hiraga, K. and Saito, H., On $L$-packets for inner forms of ${\mathrm{SL} }_{n} $, Mem. Amer. Math. Soc. 215 (2012).Google Scholar
Humbert, P., Théorie de la réduction des formes quadratiques définies positives dans un corps algébrique $K$ fini, Comment. Math. Helv. 12 (1940), 263–306.CrossRefGoogle Scholar
Iwaniec, H. and Sarnak, P., ${L}^{\infty } $ norms of eigenfunctions of arithmetic surfaces, Ann. of Math. (2) 141 (2) (1995), 301–320.CrossRefGoogle Scholar
Kitaoka, Y., Arithmetic of quadratic forms, Cambridge Tracts in Mathematics, Volume 106 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Ponomarev, P., Arithmetic of quaternary quadratic forms, Acta Arith. 29 (1) (1976), 1–48.CrossRefGoogle Scholar
Sarnak, P., Arithmetic quantum chaos, in The Schur lectures (1992) (Tel Aviv), Israel Math. Conf. Proc., Volume 8, pp. 183–236 (Bar-Ilan Univ., Ramat Gan, 1995).Google Scholar
Sarnak, P., Letter to Morawetz, available at http://www.math.princeton.edu/sarnak.Google Scholar
Templier, N., On the sup-norm of Maass cusp forms of large level, Selecta Math. 16 (2010), 501–531.Google Scholar
Templier, N., Large values of modular forms , preprint arXiv:1207.6134.Google Scholar
VanderKam, J. M., ${L}^{\infty } $ norms and quantum unique ergodicity on the sphere, Int. Math. Res. Not. 1997 (1997), 329–347.Google Scholar
Venkatesh, A., Sparse equidistribution problems, period bounds and subconvexity, Ann. of Math. (2) 172 (2) (2010), 989–1094.CrossRefGoogle Scholar
Vignéras, M.-F., Arithmétique des algèbres de quaternions, Lecture Notes in Mathematics, Volume 800 (Springer, Berlin, 1980) (in French).Google Scholar
Vilenkin, N. Ja. and Klimyk, A. U., Representation of Lie groups and special functions. Vol. 1, Mathematics and its Applications (Soviet Series), Volume 72 (Kluwer Academic Publishers Group, Dordrecht, 1991).CrossRefGoogle Scholar