Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T20:15:11.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group. III

Part of: Structure and classification of infinite or finite groups Curves General field theory

Published online by Cambridge University Press:  11 August 2009

Hiroaki Nakamura ,
Hiroshi Tsunogai  and
Seidai Yasuda
Hiroaki Nakamura
Affiliation:
Department of Mathematics, Faculty of Science, Okayama University, Okayama 700-8530, Japan ([email protected])
Hiroshi Tsunogai
Affiliation:
Department of Mathematics, Sophia University, Tokyo 102-8554, Japan ([email protected])
Seidai Yasuda
Affiliation:
Research Institute of Mathematical Science, Kyoto University, Kyoto 606-8502, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study behaviours of the ‘equianharmonic’ parameter of the Grothendieck–Teichmüller group introduced by Lochak and Schneps. Using geometric construction of a certain one-parameter family of quartics, we realize the Galois action on the fundamental group of a punctured Mordell elliptic curve in the standard Galois action on a specific subgroup of the braid group 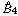. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.

Keywords

Grothendieck–Teichmüller groupGalois actions on profinite braid groupsadelic beta function

MSC classification

Secondary: 14H30: Coverings, fundamental group 20E18: Limits, profinite groups 12E12: Equations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 9 , Issue 2 , April 2010 , pp. 431 - 448
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anderson, G., The hyperadelic gamma function, Invent. Math. 95 (1989), 63–131.CrossRefGoogle Scholar
2.Belyi, G. V., On Galois extensions of a maximal cyclotomic field, Izv. Akad. Nauk SSSR Ser. Mat. 8 (1979), 267–276 (in Russian; English transl., Math. USSR Izv. 14 (1980), 247–256).Google Scholar
3.Drinfeld, V. G., On quasitriangular quasi-Hopf algebras and a group closely connected with , Algebra I Analiz 2 (1990), 149–181 (in Russian; English transl., Leningrad Math. J. 2(4) (1991), 829–860).Google Scholar
4.Gorin, E. A. and Lin, V. J., Algebraic equations with continuous coefficients, and certain questions of the algebraic theory of braids, Mat. Sb. 78 (1969), 579–610 (in Russian; English transl., Math. USSR Sb. 7 (1969), 569–596).Google Scholar
5.Grothendieck, A., Esquisse d'un Programme, 1984, in Geometric Galois actions, I (ed. Lochak, P. and Schneps, L.), London Mathematical Society Lecture Notes Series, Volume 242, pp. 5–48 (London Mathematical Society, 1997).Google Scholar
6.Ihara, Y., On beta and gamma functions associated with the Grothendieck–Teichmüller modular group, in Aspects of Galois theory (ed. Voelklein, H. et al. ), London Mathematical Society Lecture Notes Series, Volume 256, pp. 144–179 (London Mathematical Society, 1999).Google Scholar
7.Ihara, Y., On beta and gamma functions associated with the Grothendieck–Teichmüller modular group, II, J. Reine Angew. Math. 527 (2000), 1–11.CrossRefGoogle Scholar
8.Ihara, Y. and Matsumoto, M., On Galois actions on profinite completions of braid groups, in Recent developments in the inverse Galois problem (ed. Fried, M. et al. ), Contemporary Mathematics, Volume 186, pp. 173–200 (American Mathematical Society, Providence, RI, 1995).CrossRefGoogle Scholar
9.Katz, N., p-adic interpolation of real analytic Eisenstein series, Annals Math. 104 (1976), 459–571.CrossRefGoogle Scholar
10.Lochak, P. and Schneps, L., A cohomological interpretation of the Grothendieck–Teichmüller group, Invent. Math. 127 (1997), 571–600.CrossRefGoogle Scholar
11.Lochak, P., Nakamura, H. and Schneps, L., Eigenloci of 5 point configurations on the Riemann sphere and the Grothendieck–Teichmüller group, Math. J. Okayama Univ. 46 (2004), 39–75.Google Scholar
12.Mochizuki, S., The local pro-p anabelian geometry of curves, Invent. Math. 138 (1999), 319–423.CrossRefGoogle Scholar
13.Mordell, L. J., Diophantine equations (Academic Press, 1969).Google Scholar
14.Nakamura, H., Limits of Galois representations in fundamental groups along maximal degeneration of marked curves, I, Am. J. Math. 121 (1999), 315–358.CrossRefGoogle Scholar
15.Nakamura, H., Tangential base points and Eisenstein power series, in Aspects of Galois theory (ed. Voelklein, H. et al. ), London Mathematical Society Lecture Notes Series, Volume 256, pp. 202–217 (London Mathematical Society, 1999).Google Scholar
16.Nakamura, H., Some arithmetic in fundamental groups of affine elliptic curves, Talk at Euresco Conference, Acquafredda Maratea, 2001.Google Scholar
17.Nakamura, H., Limits of Galois representations in fundamental groups along maximal degeneration of marked curves, II, Proc. Symp. Pure Math. 70 (2002), 43–78.CrossRefGoogle Scholar
18.Nakamura, H. and Schneps, L., On a subgroup of the Grothendieck–Teichmüller group acting on the tower of profinite Teichmüller modular groups, Invent. Math. 141 (2000), 503–560.CrossRefGoogle Scholar
19.Nakamura, H. and Tsunogai, H., Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group, Forum Math. 15 (2003), 877–892.CrossRefGoogle Scholar
20.Nakamura, H. and Tsunogai, H., Harmonic and equianharmonic equations in the Grothendieck–Teichmüller group, II, in Primes and knots (ed. Kohno, T. and Morishita, M.), Contemporary Mathematics, Volume 416, pp. 197–211 (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
21.Tamagawa, A., The Grothendieck conjecture for affine curves, Compositio Math. 109 (1997), 135–194.CrossRefGoogle Scholar