Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T08:30:12.640Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric Weil representation in characteristic two

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  13 December 2011

Alain Genestier  and
Sergey Lysenko
Alain Genestier
Affiliation:
Institut Elie Cartan, Université Henri Poincaré Nancy 1, BP 239, F-54506 Vandoeuvre-lès-Nancy Cedex, France ([email protected]; [email protected])
Sergey Lysenko
Affiliation:
Institut Elie Cartan, Université Henri Poincaré Nancy 1, BP 239, F-54506 Vandoeuvre-lès-Nancy Cedex, France ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

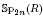Let k be an algebraically closed field of characteristic two. Let R be the ring of Witt vectors of length two over k. We construct a group stack Ĝ over k, the metaplectic extension of the Greenberg realization of . We also construct a geometric analogue of the Weil representation of Ĝ, this is a triangulated category on which Ĝ acts by functors. This triangulated category and the action are geometric in a suitable sense.

Keywords

Weil representationcharacteristic twometaplectic extension

MSC classification

Secondary: 11R39: Langlands-Weil conjectures, nonabelian class field theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 11 , Issue 2 , April 2012 , pp. 221 - 271
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Albert, A. A., Symmetric and alternate matrices in an arbitrary field, I, Trans. Am. Math. Soc. 43 (1938), 386–436Google Scholar
2.Baeza, R., Quadratic forms over semilocal rings, Lecture Notes in Mathematics, Volume 655 (Springer, 1978).CrossRefGoogle Scholar
3.Baeza, R., Some algebraic aspects of quadratic forms over fields of characteristic two, in Proceedings of the Conference on Quadratic Forms and Related Topics, Baton Rouge, LA, 2001, Documenta Mathematica Extra Volume: Quadratic Forms LSU, pp. 49–63 (2001).CrossRefGoogle Scholar
4.Bourbaki, N., Éléments des mathématiques, in Algèbre, Chapter 9, Formes sesquilinéaires et formes quadratiques (Hermann, 1959).Google Scholar
5.Breen, L., Bitorseurs et cohomologie non abélienne, pp. 401–477, Grothendieck Festschrift (Birkhäuser, 1990).Google Scholar
6.Breen, L., On the classification of 2-gerbes and 2-stacks, Astérisque, Volume 225 (Société Mathématique de France, Paris, 1994).Google Scholar
7.Brylinski, J.-L. and Deligne, P., Central extensions of reductive groups by K 2, Publ. Math. IHES 94 (2001), 5–85.CrossRefGoogle Scholar
8.Dat, J.-F., Lemme fondamental et endoscopie, une approche géométrique (d'après Laumon et Ngô), Séminaire Bourbaki (2004), Number 940, Astérisque 307 (2006), 71–112.Google Scholar
9.Gaitsgory, D., On De Jong's conjecture, Israel J. Math. 157 (2007), 155–191.CrossRefGoogle Scholar
10.Greenberg, M. J., Schemata over local rings, Annals Math. 73 (1961), 624–648.CrossRefGoogle Scholar
11.Gurevich, Sh. and Hadani, R., The Weil representation in characteristic two, Adv. Math., in press.Google Scholar
12.Hiss, G. and Zalesski, A., The Weil–Steinberg character of finite classical groups, Represent. Theory 13 (2009), 427–459.CrossRefGoogle Scholar
13.Isaacs, I. M., Characters of solvable and symplectic groups, Am. J. Math. 95 (1973), 594–635.CrossRefGoogle Scholar
14.Lafforgue, V. and Lysenko, S., Geometric Weil representation: local field case, Compositio Math. 145(1) (2009), 56–88.CrossRefGoogle Scholar
15.López-Díaz, M. C. and Rúa, I. F., An invariant for quadratic forms valued in Galois rings of characteristic 4, Finite Fields Applicat. 13 (2007), 946–961.CrossRefGoogle Scholar
16.Lysenko, S., Moduli of metaplectic bundles on curves and Theta-sheaves, Annales Scient. Éc. Norm. Sup. 39 (2006), 415–466.CrossRefGoogle Scholar
17.Moeglin, C., Vignéras, M.-F. and Waldspurger, J.-L., Correspondances de Howe sur un corps p-adique, Lecture Notes in Mathematics, Volume 1291 (Springer, 1987).CrossRefGoogle Scholar
18.Saibi, M., Transformation de Fourier–Deligne sur les groupes unipotents, Annales Inst. Fourier 46(5) (1996), 1205–1242.CrossRefGoogle Scholar
19.Suprunenko, D. A., Soluble and nilpotent linear groups (Belorussian University Press, Minsk, 1958) (in Russian; English translation: American Mathematical Society, Providence, RI, 1963).Google Scholar
20.Thomas, T., The Maslov index as a quadratic space, Math. Res. Lett. 13(6) (2006), 985–999.CrossRefGoogle Scholar
21.Weil, A., Sur certains groupes d'opérateurs unitaires, Acta Math. 111 (1964), 143–211.CrossRefGoogle Scholar
22.Wood, J. A., Witt's extension theorem for mod four valued quadratic forms, Trans. Am. Math. Soc. 336(1) (1993), 445–461.Google Scholar