Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T16:06:53.789Z Has data issue: false hasContentIssue false
  • English
  • Français

GEOMETRIC LOCAL 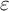$\varepsilon $-FACTORS IN HIGHER DIMENSIONS

Part of: (Co)homology theory

Published online by Cambridge University Press:  02 September 2021

Quentin Guignard Open the ORCID record for Quentin Guignard [Opens in a new window]
Quentin Guignard*
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, 53111Bonn, Germany ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a product formula for the determinant of the cohomology of an étale sheaf with 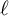$\ell $ -adic coefficients over an arbitrary proper scheme over a perfect field of positive characteristic p distinct from 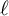$\ell $ . The local contributions are constructed by iterating vanishing cycle functors as well as certain exact additive functors that can be considered as linearised versions of Artin conductors and local 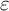$\varepsilon $ -factors. 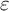We provide several applications of our higher dimensional product formula, such as twist formulas for global $\varepsilon $ -factors.

Keywords

étale cohomologyε-factorsconductors

MSC classification

Primary: 14F20: Étale and other Grothendieck topologies and (co)homologies
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 1887 - 1913
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Deligne, P., Les constantes des équations fonctionnelles des fonctions $L$ [Constants of functional equations of $L$ -functions], in Modular Functions of One Variable II, Lecture Notes in Mathematics, Vol. 349, pp. 501–597 (Springer-Verlag, Berlin, 1973).10.1007/978-3-540-37855-6_7CrossRefGoogle Scholar
Deligne, P., Séminaire de Géométrie Algébrique du Bois Marie–Cohomologie étale [Étale cohomology] (SGA 4 1/2), Lecture Notes in Mathematics, Vol. 569 (Springer-Verlag, Berlin, 1977).Google Scholar
Deligne, P. and Katz, N., Séminaire de Géométrie Algébrique du Bois Marie–1967–69–Groupes de monodromie en géométrie algébrique [Monodromy groups in algebraic geometry] (SGA 7), Vol. 2, Lecture Notes in Mathematics, Vol. 340 (Springer-Verlag, Berlin, 1973).Google Scholar
Dwork, B., On the Artin root number, Amer. J. Math. 78 (1956), 444–472.10.2307/2372524CrossRefGoogle Scholar
Grothendieck, A., Séminaire de Géométrie Algébrique du Bois Marie–1963–64–Théorie des topos et cohomologie étale des schémas [Topos theory and étale cohomology of schemes] SGA 4), Lecture Notes in Mathematics, Vols. 269, 270, 305 (Springer-Verlag, Berlin, 1972–1973).Google Scholar
Guignard, Q., Geometric local epsilon factors, arxiv:1902.06523 (v3), 2019.Google Scholar
LUC Illusie, Théorie de Brauer et caractéristique d’Euler-Poincaré d’après P. Deligne [Brauer theory and Euler-Poincaré characteristic, after P. Deligne], Astérisque 82–83 (1981), 161–172.Google Scholar
Kato, K. and Saito, S., Unramified class field theory of arithmetical surfaces, Ann. Math. 118 (1983), 241–275.10.2307/2007029CrossRefGoogle Scholar
Katz, N. M., Local-to-global extensions of representations of fundamental groups, Ann. Inst. Fourier 36(4) (1986), 69–106.10.5802/aif.1069CrossRefGoogle Scholar
Laumon, G., Transformation de Fourier, constantes d’équations fonctionnelles et conjecture de Weil [Fourier transform, constants of functional equations and Weil conjectures], Pub. Math. I.H.E.S. 65 (1987), 131–210.10.1007/BF02698937CrossRefGoogle Scholar
Saito, T., The characteristic cycle and the singular support of a constructible sheaf, Invent. Math. 207(2) (2017), 597–695.10.1007/s00222-016-0675-3CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu, 2019.Google Scholar
Takeuchi, D., Characteristic epsilon cycles of $\ell$ -adic sheaves on varieties, arxiv:1911.02269, 2019.Google Scholar
Umezaki, N., Yang, E. and Zhao, Y., Characteristic class and the epsilon factor of an étale sheaf, arxiv:1701.02841, 2018.Google Scholar
Vidal, I., Théorie de Brauer et conducteur de Swan [Brauer theory and Swan conductor], J. Algebr. Geom. 13 (2004), 349–391.10.1090/S1056-3911-03-00336-9CrossRefGoogle Scholar
Yasuda, S., Local ${\varepsilon}_0$ -characters in torsion rings, J. Théor. Nombres Bordeaux 19 (2007), 763–797.10.5802/jtnb.611CrossRefGoogle Scholar
Yasuda, S., Local constants in torsion rings, J. Math. Sci. (Univ. Tokyo) 16(2) (2009), 125–197.Google Scholar
Yasuda, S., The product formula for local constants in torsion rings, J. Math. Sci. (Univ. Tokyo) 16(2) (2009), 199–230.Google Scholar