Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-16T09:16:38.067Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERAL HYPERPLANE SECTIONS OF LOG CANONICAL THREEFOLDS IN POSITIVE CHARACTERISTIC

Part of: Local theory Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  14 April 2025

Kenta Sato Open the ORCID record for Kenta Sato [Opens in a new window]
Kenta Sato*
Affiliation:
Department of Mathematics and Informatics, Chiba University, 1-33, Yayoicho, Inage-ku, Chiba-shi, Chiba, 263-8522, Japan
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove that if a three-dimensional quasi-projective variety X over an algebraically closed field of characteristic 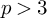$p>3$ has only log canonical singularities, then so does a general hyperplane section H of X. We also show that the same is true for klt singularities, which is a slight extension of [15]. In the course of the proof, we provide a sufficient condition for log canonical (resp. klt) surface singularities to be geometrically log canonical (resp. geometrically klt) over a field.

Keywords

Bertini theoremgeometrically log canonical singularitiessurface singularitiesdual graph

MSC classification

Primary: 14B05: Singularities
Secondary: 14J17: Singularities
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , First View , pp. 1 - 28
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bǎdescu, L (2001) Algebraic Surfaces. New York: Springer.CrossRefGoogle Scholar
Caterina, C, Greco, S and Manaresi, M (1986) An axiomatic approach to the second theorem of Bertini. J. Algebra 98(1), 171–182.Google Scholar
Debarre, O (2001) Higher-Dimensional Algebraic Geometry, vol. 3. New York: Springer.CrossRefGoogle Scholar
Grothendieck, A (1966) Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Troisième partie. Publ. Math. Inst. Hautes Études Sci. 28, 5–255.CrossRefGoogle Scholar
Fulton, W (2013) Intersection Theory, vol. 2. Springer Science & Business Media.Google Scholar
Hartshorne, R (1977) Algebraic Geometry. Graduate Texts in Mathematics, vol. 52. Berlin: Springer-Verlag.CrossRefGoogle Scholar
Huneke, C and Swanson, I (2006) Integral Closure of Ideals, Rings, and Modules. Cambridge: Cambridge University Press.Google Scholar
Ji, L and Waldron, J (2021) Structure of geometrically non-reduced varieties. Trans. Amer. Math. Soc. 374(12), 8333–8363.CrossRefGoogle Scholar
Kollár, J (2013) Singularities of the Minimal Model Program, vol. 200. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Kollár, J and Mori, S (1998) Birational Geometry of Algebraic Varieties. Cambridge Tracts in Mathematics, vol. 134. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Matsumura, H (1989) Commutative Ring Theory, Reid M (trans.), 2nd edn. Cambridge Studies in Advanced Mathematics, vol. 8. Cambridge: Cambridge University Press.Google Scholar
Zs, Patakfalviand Waldron, J (2022) Singularities of general fibers and the LMMP. Amer. J. Math. 144(2), 505–540.Google Scholar
Reid, M (1980) Canonical 3-folds. In Beauville A (ed), Journées de géométrie algébrique d’Angers 1979. Alphen: Sijthoff & Noordhoff, 273–310.Google Scholar
Schröer, S (2009) On genus change in algebraic curves over imperfect fields. Proc. Amer. Math. Soc. 137(4), 1239–1243.CrossRefGoogle Scholar
Sato, K and Takagi, S (2020) General hyperplane sections of threefolds in positive characteristic. J. Inst. Math. Jussieu 19(2), 647–661.CrossRefGoogle Scholar
Sato, K and Takagi, S, (2021) Arithmetic and geometric deformations of F-pure and F-regular singularities. arXiv preprint 2103.03721, to appear in Amer. J. Math. Google Scholar
The Stacks Project Authors, The Stacks Project.Google Scholar
Tanaka, H (2021) Invariants of algebraic varieties over imperfect fields. Tohoku Math. J. (2) 73( 4), 471–538.CrossRefGoogle Scholar
Tate, J (1952) Genus change in inseparable extensions of function fields . Proc. Amer. Math. 3(3), 400–406.CrossRefGoogle Scholar