1. Introduction: the notion of a contactification
A contact structure
![]() $(M,{\mathcal D})$
on a
$(M,{\mathcal D})$
on a
![]() $(2n+1)$
dimensional real manifold M is usually defined in terms of a 1-form
$(2n+1)$
dimensional real manifold M is usually defined in terms of a 1-form
![]() $\lambda $
on M such that
$\lambda $
on M such that
at each point
![]() $x\in M$
. Given such a 1-form, the contact structure
$x\in M$
. Given such a 1-form, the contact structure
![]() $(M,{\mathcal D})$
on M is the rank
$(M,{\mathcal D})$
on M is the rank
![]() $s=2n$
vector distribution
$s=2n$
vector distribution
Note that any
![]() $\lambda '=a\lambda $
, with a being a nonvanishing function on M, defines the same contact structure
$\lambda '=a\lambda $
, with a being a nonvanishing function on M, defines the same contact structure
![]() $(M,{\mathcal D})$
. We also note that given a contact structure
$(M,{\mathcal D})$
. We also note that given a contact structure
![]() $(M,{\mathcal D})$
, we additionally have a family of 2-forms on M
$(M,{\mathcal D})$
, we additionally have a family of 2-forms on M
where
![]() $a\neq 0$
is a function, and
$a\neq 0$
is a function, and
![]() $\mu $
is a 1-form on M. This, in particular, means that given a contact structure
$\mu $
is a 1-form on M. This, in particular, means that given a contact structure
![]() $(M,{\mathcal D})$
, we have a rank
$(M,{\mathcal D})$
, we have a rank
![]() $s=2n$
(bracket generating) distribution
$s=2n$
(bracket generating) distribution
![]() ${\mathcal D}$
, and a line of a closed 2-form
${\mathcal D}$
, and a line of a closed 2-form
![]() $\omega $
in the distribution
$\omega $
in the distribution
![]() ${\mathcal D}$
, with
${\mathcal D}$
, with
This can be compared with the notion of a symplectic structure
![]() $(N,[\omega ])$
on a
$(N,[\omega ])$
on a
![]() $s=2n$
dimensional real manifold N. Such a structure is defined in terms of a line
$s=2n$
dimensional real manifold N. Such a structure is defined in terms of a line
![]() $\omega '=h\omega $
of a nowhere vanishing 2-form
$\omega '=h\omega $
of a nowhere vanishing 2-form
![]() $\omega $
on N, such that
$\omega $
on N, such that
Here, contrary to the contact case, we have a line of a closed 2-form
![]() $\omega $
in the tangent space
$\omega $
in the tangent space
![]() $\mathrm {T}N$
rather than in the proper vector subbundle
$\mathrm {T}N$
rather than in the proper vector subbundle
![]() ${\mathcal D}\subsetneq \mathrm {T}N$
.
${\mathcal D}\subsetneq \mathrm {T}N$
.
By the Poincaré lemma, locally, in an open set
![]() ${\mathcal O}\subset N$
, the form
${\mathcal O}\subset N$
, the form
![]() $\omega $
defines a 1-form
$\omega $
defines a 1-form
![]() $\Lambda $
on N such
$\Lambda $
on N such
![]() $\mathrm {d}\Lambda =\omega $
. Therefore, given a symplectic structure
$\mathrm {d}\Lambda =\omega $
. Therefore, given a symplectic structure
![]() $(N,[\omega ])$
, we can locally contactify it by considering a
$(N,[\omega ])$
, we can locally contactify it by considering a
![]() $(2n+1)$
dimensional manifold
$(2n+1)$
dimensional manifold
with a 1-form
on
![]() $\mathcal U$
; here, the real variable u is a coordinate along the
$\mathcal U$
; here, the real variable u is a coordinate along the
![]() $\mathbb {R}$
factor in
$\mathbb {R}$
factor in
![]() $\mathcal U=\mathbb {R}\times \mathcal O$
. As a result, the structure
$\mathcal U=\mathbb {R}\times \mathcal O$
. As a result, the structure
![]() $(M,{\mathcal D})=\big ({\mathcal U},\ker (\lambda )\big )$
is a contact structure, called a contact structure associated with the symplectic structure
$(M,{\mathcal D})=\big ({\mathcal U},\ker (\lambda )\big )$
is a contact structure, called a contact structure associated with the symplectic structure
![]() $(N,[\omega ])$
.
$(N,[\omega ])$
.
We introduce the notion of a contactification as a generalisation of the above considerations.
Definition 1.1. Let N be an s-dimensional manifold and let
![]() $\mathrm {d}{\mathcal D}^\perp :=\mathrm {Span}(\omega ^1,\omega ^2, \dots ,\omega ^r)$
be a rank r subbundle of
$\mathrm {d}{\mathcal D}^\perp :=\mathrm {Span}(\omega ^1,\omega ^2, \dots ,\omega ^r)$
be a rank r subbundle of
![]() $\bigwedge ^2N$
. Consider an
$\bigwedge ^2N$
. Consider an
![]() $(s+r)$
-dimensional fiber bundle
$(s+r)$
-dimensional fiber bundle
![]() $F\to M\stackrel {\pi }{\to }N$
over N. Let
$F\to M\stackrel {\pi }{\to }N$
over N. Let
![]() $(X_1,X_2,\dots , X_r)$
be a coframe of vertical vectors in M. In particular, we have
$(X_1,X_2,\dots , X_r)$
be a coframe of vertical vectors in M. In particular, we have
![]() $\pi _*(X_i)=0$
for all
$\pi _*(X_i)=0$
for all
![]() $i=1,2,\dots ,r$
.
$i=1,2,\dots ,r$
.
Let us assume that on M there exist r one-forms
![]() $\lambda ^i$
,
$\lambda ^i$
,
![]() $i=1,2,\dots ,r$
, such that
$i=1,2,\dots ,r$
, such that ![]() on M, and that
on M, and that
![]() $\mathrm {d}\lambda ^i=\sum _{j=1}^r a^i{}_j\pi ^*(\omega ^j)+\sum _{j=1}^r\mu ^i{}_j\wedge \lambda ^j$
for all
$\mathrm {d}\lambda ^i=\sum _{j=1}^r a^i{}_j\pi ^*(\omega ^j)+\sum _{j=1}^r\mu ^i{}_j\wedge \lambda ^j$
for all
![]() $i=1,2,\dots r$
, with some 1-forms
$i=1,2,\dots r$
, with some 1-forms
![]() $\mu ^i{}_j$
and some functions
$\mu ^i{}_j$
and some functions
![]() $a^i{}_j$
on M satisfying
$a^i{}_j$
on M satisfying
![]() $\mathrm {det}(a^i{}_j)\neq 0$
. Consider the corresponding rank s distribution
$\mathrm {det}(a^i{}_j)\neq 0$
. Consider the corresponding rank s distribution ![]() on M.
on M.
Then the pair
![]() $(M,{\mathcal D})$
is called a contactification of the pair
$(M,{\mathcal D})$
is called a contactification of the pair
![]() $(N,\mathrm {d} {\mathcal D}^\perp )$
.
$(N,\mathrm {d} {\mathcal D}^\perp )$
.
Definition 1.2. A real Lie algebra
![]() $\mathfrak {g}$
spanned over
$\mathfrak {g}$
spanned over
![]() $\mathbb {R}$
by the vector fields Y on M of the contactification
$\mathbb {R}$
by the vector fields Y on M of the contactification
![]() $(M,{\mathcal D})$
satisfying
$(M,{\mathcal D})$
satisfying
is called the Lie algebra of infinitesimal symmetries of the contactification
![]() $(M,{\mathcal D})$
. By definition, it is the same as the Lie algebra of infinitesimal symmetries of the distribution
$(M,{\mathcal D})$
. By definition, it is the same as the Lie algebra of infinitesimal symmetries of the distribution
![]() ${\mathcal D}$
on M. The vector fields Y on
${\mathcal D}$
on M. The vector fields Y on
![]() $(M,{\mathcal D})$
satisfying (1.1) are called infinitesimal symmetries of
$(M,{\mathcal D})$
satisfying (1.1) are called infinitesimal symmetries of
![]() $(M,{\mathcal D})$
, or of
$(M,{\mathcal D})$
, or of
![]() $\mathcal D$
, for short.
$\mathcal D$
, for short.
Below, we give a nontrivial example of the notions included in Definitions 1.1 and 1.2.
Example 1.3. Consider
![]() $N=\mathbb {R}^8$
with Cartesian coordinates
$N=\mathbb {R}^8$
with Cartesian coordinates
![]() $(x^1,x^2, x^{3},x^{4},x^{5},x^{6}, x^{7},x^{8})$
and a space
$(x^1,x^2, x^{3},x^{4},x^{5},x^{6}, x^{7},x^{8})$
and a space
![]() $\mathrm {d}{\mathcal D}^\perp =\mathrm {Span}(\omega ^1,\omega ^2,\omega ^3,\omega ^4,\omega ^5,\omega ^6,\omega ^7)\subset \bigwedge ^2N$
, which is spanned by the following seven 2-forms on N:
$\mathrm {d}{\mathcal D}^\perp =\mathrm {Span}(\omega ^1,\omega ^2,\omega ^3,\omega ^4,\omega ^5,\omega ^6,\omega ^7)\subset \bigwedge ^2N$
, which is spanned by the following seven 2-forms on N:
 $$ \begin{align*}\begin{aligned} \omega^1=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{8}+\mathrm{d} x^2\wedge\mathrm{d} x^{5}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{7}+\mathrm{d} x^{4}\wedge\mathrm{d} x^{6}\\ \omega^2=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{5}+\mathrm{d} x^2\wedge\mathrm{d} x^{8}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{6}-\mathrm{d} x^{4}\wedge\mathrm{d} x^{7}\\ \omega^3=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{7}-\mathrm{d} x^2\wedge\mathrm{d} x^{6}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{8}+\mathrm{d} x^{4}\wedge\mathrm{d} x^{5}\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \omega^1=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{8}+\mathrm{d} x^2\wedge\mathrm{d} x^{5}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{7}+\mathrm{d} x^{4}\wedge\mathrm{d} x^{6}\\ \omega^2=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{5}+\mathrm{d} x^2\wedge\mathrm{d} x^{8}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{6}-\mathrm{d} x^{4}\wedge\mathrm{d} x^{7}\\ \omega^3=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{7}-\mathrm{d} x^2\wedge\mathrm{d} x^{6}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{8}+\mathrm{d} x^{4}\wedge\mathrm{d} x^{5}\end{aligned} \end{align*} $$
 $$ \begin{align*}\begin{aligned}\omega^4=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{2}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{4}+\mathrm{d} x^{5}\wedge\mathrm{d} x^{8}+\mathrm{d} x^{6}\wedge\mathrm{d} x^{7}\\ \omega^5=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{6}+\mathrm{d} x^2\wedge\mathrm{d} x^{7}-\mathrm{d} x^{3}\wedge\mathrm{d} x^{5}+\mathrm{d} x^{4}\wedge\mathrm{d} x^{8}\\ \omega^6=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{4}+\mathrm{d} x^2\wedge\mathrm{d} x^{3}-\mathrm{d} x^{5}\wedge\mathrm{d} x^{7}+\mathrm{d} x^{6}\wedge\mathrm{d} x^{8}\\ \omega^7=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{3}-\mathrm{d} x^2\wedge\mathrm{d} x^{4}+\mathrm{d} x^{5}\wedge\mathrm{d} x^{6}+\mathrm{d} x^{7}\wedge\mathrm{d} x^{8}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned}\omega^4=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{2}+\mathrm{d} x^{3}\wedge\mathrm{d} x^{4}+\mathrm{d} x^{5}\wedge\mathrm{d} x^{8}+\mathrm{d} x^{6}\wedge\mathrm{d} x^{7}\\ \omega^5=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{6}+\mathrm{d} x^2\wedge\mathrm{d} x^{7}-\mathrm{d} x^{3}\wedge\mathrm{d} x^{5}+\mathrm{d} x^{4}\wedge\mathrm{d} x^{8}\\ \omega^6=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{4}+\mathrm{d} x^2\wedge\mathrm{d} x^{3}-\mathrm{d} x^{5}\wedge\mathrm{d} x^{7}+\mathrm{d} x^{6}\wedge\mathrm{d} x^{8}\\ \omega^7=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{3}-\mathrm{d} x^2\wedge\mathrm{d} x^{4}+\mathrm{d} x^{5}\wedge\mathrm{d} x^{6}+\mathrm{d} x^{7}\wedge\mathrm{d} x^{8}. \end{aligned} \end{align*} $$
As the bundle N, take
![]() $M=\mathbb {R}^{7}\times \mathbb {R}^8\to N$
with coordinates
$M=\mathbb {R}^{7}\times \mathbb {R}^8\to N$
with coordinates
![]() $(x^1,\dots ,x^8,x^9\dots ,x^{15})$
, and take seven 1-forms
$(x^1,\dots ,x^8,x^9\dots ,x^{15})$
, and take seven 1-forms
 $$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} x^9+ x^1\mathrm{d} x^{8}+ x^2\mathrm{d} x^{5}+ x^{3}\mathrm{d} x^{7}+ x^{4}\mathrm{d} x^{6}\\ \lambda^2=\,\,&\mathrm{d} x^{10} - x^1\mathrm{d} x^{5}+ x^2\mathrm{d} x^{8}+ x^{3}\mathrm{d} x^{6}- x^{4}\mathrm{d} x^{7}\\ \lambda^3=\,\,&\mathrm{d} x^{11} - x^1\mathrm{d} x^{7}- x^2\mathrm{d} x^{6}+ x^{3}\mathrm{d} x^{8}+ x^{4}\mathrm{d} x^{5}\\ \lambda^4=\,\,&\mathrm{d} x^{12} + x^1\mathrm{d} x^{2}+ x^{3}\mathrm{d} x^{4}+ x^{5}\mathrm{d} x^{8}+ x^{6}\mathrm{d} x^{7})\\ \lambda^5=\,\,&\mathrm{d} x^{13}- x^1\mathrm{d} x^{6}+ x^2\mathrm{d} x^{7}- x^{3}\mathrm{d} x^{5}+ x^{4}\mathrm{d} x^{8}\\ \lambda^6=\,\,&\mathrm{d} x^{14}+ x^1\mathrm{d} x^{4}+ x^2\mathrm{d} x^{3}- x^{5}\mathrm{d} x^{7}+ x^{6}\mathrm{d} x^{8}\\ \lambda^7=\,\,&\mathrm{d} x^{15}+ x^1\mathrm{d} x^{3}- x^2\mathrm{d} x^{4}+ x^{5}\mathrm{d} x^{6}+ x^{7}\mathrm{d} x^{8}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} x^9+ x^1\mathrm{d} x^{8}+ x^2\mathrm{d} x^{5}+ x^{3}\mathrm{d} x^{7}+ x^{4}\mathrm{d} x^{6}\\ \lambda^2=\,\,&\mathrm{d} x^{10} - x^1\mathrm{d} x^{5}+ x^2\mathrm{d} x^{8}+ x^{3}\mathrm{d} x^{6}- x^{4}\mathrm{d} x^{7}\\ \lambda^3=\,\,&\mathrm{d} x^{11} - x^1\mathrm{d} x^{7}- x^2\mathrm{d} x^{6}+ x^{3}\mathrm{d} x^{8}+ x^{4}\mathrm{d} x^{5}\\ \lambda^4=\,\,&\mathrm{d} x^{12} + x^1\mathrm{d} x^{2}+ x^{3}\mathrm{d} x^{4}+ x^{5}\mathrm{d} x^{8}+ x^{6}\mathrm{d} x^{7})\\ \lambda^5=\,\,&\mathrm{d} x^{13}- x^1\mathrm{d} x^{6}+ x^2\mathrm{d} x^{7}- x^{3}\mathrm{d} x^{5}+ x^{4}\mathrm{d} x^{8}\\ \lambda^6=\,\,&\mathrm{d} x^{14}+ x^1\mathrm{d} x^{4}+ x^2\mathrm{d} x^{3}- x^{5}\mathrm{d} x^{7}+ x^{6}\mathrm{d} x^{8}\\ \lambda^7=\,\,&\mathrm{d} x^{15}+ x^1\mathrm{d} x^{3}- x^2\mathrm{d} x^{4}+ x^{5}\mathrm{d} x^{6}+ x^{7}\mathrm{d} x^{8}. \end{aligned} \end{align*} $$
This defines a rank 8 distribution ![]() on M. The pair
on M. The pair
![]() $\big (M,{\mathcal D}\big )$
is a contactification of
$\big (M,{\mathcal D}\big )$
is a contactification of
![]() $(N,d{\mathcal D}^\perp )$
since
$(N,d{\mathcal D}^\perp )$
since
![]() $X_i=\partial _{i+8}$
,
$X_i=\partial _{i+8}$
, ![]() , and
, and
![]() $\mathrm {d}\lambda ^i=\omega ^i$
for all
$\mathrm {d}\lambda ^i=\omega ^i$
for all
![]() $i=1,\dots ,7$
. In particular, in this example, the rank 8 distribution
$i=1,\dots ,7$
. In particular, in this example, the rank 8 distribution
![]() ${\mathcal D}$
gives a 2-step filtration
${\mathcal D}$
gives a 2-step filtration
![]() ${\mathcal D}_{-1}\subset \mathcal {D}_{-2}=\mathrm {T}M$
, where
${\mathcal D}_{-1}\subset \mathcal {D}_{-2}=\mathrm {T}M$
, where
![]() ${\mathcal D}_{-1}={\mathcal D}$
and
${\mathcal D}_{-1}={\mathcal D}$
and
![]() $\mathcal {D}_{-2}=[{\mathcal D}_{-1},{\mathcal D}_{-1}]=\mathrm {T}M$
.
$\mathcal {D}_{-2}=[{\mathcal D}_{-1},{\mathcal D}_{-1}]=\mathrm {T}M$
.
This example is essentially taken from Èlie Cartan’s PhD thesis [Reference Cartan8] – actually its German version. We took it as our example inspired by the following quote from Sigurdur Helgason [Reference Helgason13]:
Cartan represented [the simple exceptional Lie group]
![]() $\mathbf {F}_4$
(...) by the Pfaffian system in
$\mathbf {F}_4$
(...) by the Pfaffian system in
![]() $\mathbb {R}^{15}$
(...). Similar results for
$\mathbb {R}^{15}$
(...). Similar results for
![]() $\mathbf {E}_6$
in
$\mathbf {E}_6$
in
![]() $\mathbb {R}^{16}$
,
$\mathbb {R}^{16}$
,
![]() $\mathbf {E}_7$
in
$\mathbf {E}_7$
in
![]() $\mathbb {R}^{27}$
and
$\mathbb {R}^{27}$
and
![]() $\mathbf {E}_8$
in
$\mathbf {E}_8$
in
![]() $\mathbb {R}^{29}$
are indicated in [Reference Cartan8]. Unfortunately, detailed proofs of these remarkable representations of the exceptional groups do not seem to be available.
$\mathbb {R}^{29}$
are indicated in [Reference Cartan8]. Unfortunately, detailed proofs of these remarkable representations of the exceptional groups do not seem to be available.
The 15-dimensional contactification
![]() $(M,{\mathcal D})$
from our Example 1.3 is obtained in terms of the seven 1-forms
$(M,{\mathcal D})$
from our Example 1.3 is obtained in terms of the seven 1-forms
![]() $\lambda ^i$
, which are equivalent to the seven forms from the Cartan Pfaffian system in dimension 15 mentioned by Helgason. In particular, it follows that the distribution structure
$\lambda ^i$
, which are equivalent to the seven forms from the Cartan Pfaffian system in dimension 15 mentioned by Helgason. In particular, it follows that the distribution structure
![]() $(M,{\mathcal D})$
has the simple exceptional Lie group
$(M,{\mathcal D})$
has the simple exceptional Lie group
![]() $\mathbf {F}_4$
, actually its real form
$\mathbf {F}_4$
, actually its real form
![]() $F_I$
in the terminology of [Reference Čap and Slovák11], as a group of authomorphism.
$F_I$
in the terminology of [Reference Čap and Slovák11], as a group of authomorphism.
In this paper, we will explain how one gets this realisation of the exceptional Lie group
![]() $\mathbf {F}_4$
, a realisation of its real form
$\mathbf {F}_4$
, a realisation of its real form
![]() $F_{II}$
, and realisations of the two (out of 5) real forms
$F_{II}$
, and realisations of the two (out of 5) real forms
![]() $E_I$
and
$E_I$
and
![]() $E_{IV}$
of the complex simple exceptional Lie group
$E_{IV}$
of the complex simple exceptional Lie group
![]() $\mathbf {E}_6$
. For this explanation, we need some preparations consisting of recalling few notions associated with vector distributions on manifolds and spinorial representations of the orthogonal groups in space of real spinors.
$\mathbf {E}_6$
. For this explanation, we need some preparations consisting of recalling few notions associated with vector distributions on manifolds and spinorial representations of the orthogonal groups in space of real spinors.
Finally, we note that our approach in this paper is purely utilitarian. We answer the question: How to get the explicit formulas in Cartesian coordinates for Pfaffian forms
![]() $(\lambda ^1,\dots ,\lambda ^r)$
, which have simple Lie algebras as symmetries? One can study more general problems related to this on purely Lie theoretical ground. For example, one can ask when a 2-step graded nilpotent Lie algebra
$(\lambda ^1,\dots ,\lambda ^r)$
, which have simple Lie algebras as symmetries? One can study more general problems related to this on purely Lie theoretical ground. For example, one can ask when a 2-step graded nilpotent Lie algebra ![]() has a given Lie algebra
has a given Lie algebra
![]() $\mathfrak {n}_{00}$
as a part of its Lie algebra
$\mathfrak {n}_{00}$
as a part of its Lie algebra
![]() $\mathfrak {n}_0$
of derivations preserving the strata, or a question as to when the Tanaka prolongation of such
$\mathfrak {n}_0$
of derivations preserving the strata, or a question as to when the Tanaka prolongation of such ![]() with
with
![]() $\mathfrak {n}_{00}\subset \mathfrak {n}_0$
is finite, or simple. This is beyond the scope of our paper. A reader interested in such problems may consult, for example, [Reference Alekseevsky and Cortes3, Reference Altomani and Santi4, Reference Molina, Kruglikov, Markina and Vasil’ev16]. We also mention that since in this paper we only consider distributions
$\mathfrak {n}_{00}\subset \mathfrak {n}_0$
is finite, or simple. This is beyond the scope of our paper. A reader interested in such problems may consult, for example, [Reference Alekseevsky and Cortes3, Reference Altomani and Santi4, Reference Molina, Kruglikov, Markina and Vasil’ev16]. We also mention that since in this paper we only consider distributions
![]() $\mathcal D$
with 2-step filtrations
$\mathcal D$
with 2-step filtrations
![]() ${\mathcal D}={\mathcal D}_{-1}\subset {\mathcal D}_{-2}=\mathrm {T}M$
and without any additional geometric structure intentionally imposed on
${\mathcal D}={\mathcal D}_{-1}\subset {\mathcal D}_{-2}=\mathrm {T}M$
and without any additional geometric structure intentionally imposed on
![]() $\mathcal D$
, the realisations of the real forms of the exceptional simple Lie group
$\mathcal D$
, the realisations of the real forms of the exceptional simple Lie group
![]() $\mathbf {G}_2$
will not appear. These can be found, for example, in [Reference Anderson, Nie and Nurowski1, Reference Biquard6, Reference Cartan10, Reference Nurowski17].
$\mathbf {G}_2$
will not appear. These can be found, for example, in [Reference Anderson, Nie and Nurowski1, Reference Biquard6, Reference Cartan10, Reference Nurowski17].
2. Magical equation for a contactification
The purpose of this section is to prove the following crucial lemma about a certain algebraic equation, which we call a magical equation. It is the boxed equation (2.1) below.
Lemma 2.1. Let
![]() $(\mathfrak {n}_{00},[\cdot ,\cdot ]_0)$
be a finite dimensional Lie algebra, and let
$(\mathfrak {n}_{00},[\cdot ,\cdot ]_0)$
be a finite dimensional Lie algebra, and let
![]() $\rho :\mathfrak {n}_{00}\stackrel {\mathrm {hom}}{\to } \mathrm {End}(S)$
be its finite dimensional representation in a real vector space S of dimension s. In addition, let R be an r-dimensional real vector space, and
$\rho :\mathfrak {n}_{00}\stackrel {\mathrm {hom}}{\to } \mathrm {End}(S)$
be its finite dimensional representation in a real vector space S of dimension s. In addition, let R be an r-dimensional real vector space, and
![]() $\tau :\mathfrak {n}_{00}\to \mathrm {End}(R)$
, be a linear map. Finally, let
$\tau :\mathfrak {n}_{00}\to \mathrm {End}(R)$
, be a linear map. Finally, let
![]() $\omega $
be a linear map
$\omega $
be a linear map
![]() $\omega :\bigwedge ^2S\to R$
, or what is the same, let
$\omega :\bigwedge ^2S\to R$
, or what is the same, let
![]() $\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
.
$\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
.
Suppose now that the triple
![]() $(\rho ,\omega ,\tau )$
satisfies the following equation:
$(\rho ,\omega ,\tau )$
satisfies the following equation:
for all
![]() $A\in \mathfrak {n}_{00}$
and all
$A\in \mathfrak {n}_{00}$
and all
![]() $X,Y\in S$
. Then we have the following:
$X,Y\in S$
. Then we have the following:
-
(1) The map
 $\tau $
satisfies
$\tau $
satisfies  $$ \begin{align*}\big(\,\,\tau([A,B]_0)-[\tau(A),\tau(B)]_{\mathrm{End}(R)}\,\,\big)\omega\,\,=\,\,0\quad\quad \forall\,\,A,B\in\mathfrak{n}_{00}.\end{align*} $$
$$ \begin{align*}\big(\,\,\tau([A,B]_0)-[\tau(A),\tau(B)]_{\mathrm{End}(R)}\,\,\big)\omega\,\,=\,\,0\quad\quad \forall\,\,A,B\in\mathfrak{n}_{00}.\end{align*} $$
-
(2) If the map
 $\tau :\mathfrak {n}_{00}\to \mathrm {End}(R)$
is a representation of
$\tau :\mathfrak {n}_{00}\to \mathrm {End}(R)$
is a representation of
 $\mathfrak {n}_{00}$
, that is, if then the real vector space
$\mathfrak {n}_{00}$
, that is, if then the real vector space $$ \begin{align*}\tau([A,B]_0)=[\tau(A),\tau(B)]_{\mathrm{End}(R)},\end{align*} $$
$$ \begin{align*}\tau([A,B]_0)=[\tau(A),\tau(B)]_{\mathrm{End}(R)},\end{align*} $$
 $\mathfrak {g}_0:=R\oplus S\oplus \mathfrak {n}_{00}$
is a graded Lie algebra with the graded components
$\mathfrak {g}_0:=R\oplus S\oplus \mathfrak {n}_{00}$
is a graded Lie algebra with the graded components $$ \begin{align*}\mathfrak{g}_0=\mathfrak{n}_{-2}\oplus\mathfrak{n}_{-1}\oplus\mathfrak{n}_{00},\end{align*} $$
and with the Lie bracket
$$ \begin{align*}\mathfrak{g}_0=\mathfrak{n}_{-2}\oplus\mathfrak{n}_{-1}\oplus\mathfrak{n}_{00},\end{align*} $$
and with the Lie bracket $$ \begin{align*}\mathfrak{n}_{-2}=R,\quad \mathfrak{n}_{-1}=S,\quad\mathrm{with}\,\, \mathfrak{n}_{00}\,\,\mathrm{as\,\,the}\,\,0\,\,\mathrm{grade},\end{align*} $$
$$ \begin{align*}\mathfrak{n}_{-2}=R,\quad \mathfrak{n}_{-1}=S,\quad\mathrm{with}\,\, \mathfrak{n}_{00}\,\,\mathrm{as\,\,the}\,\,0\,\,\mathrm{grade},\end{align*} $$
 $[\cdot ,\cdot ]$
given by
$[\cdot ,\cdot ]$
given by
-
(a) if
 $X,Y\in \mathfrak {n}_{00}$
, then
$X,Y\in \mathfrak {n}_{00}$
, then
 $[X,Y]=[X,Y]_0$
,
$[X,Y]=[X,Y]_0$
, -
(b) if
 $A\in \mathfrak {n}_{00}$
,
$A\in \mathfrak {n}_{00}$
,
 $X\in \mathfrak {n}_{-1}$
, then
$X\in \mathfrak {n}_{-1}$
, then
 $[A,X]=\rho (A)X$
,
$[A,X]=\rho (A)X$
, -
(c) if
 $A\in \mathfrak {n}_{00}$
,
$A\in \mathfrak {n}_{00}$
,
 $X\in \mathfrak {n}_{-2}$
, then
$X\in \mathfrak {n}_{-2}$
, then
 $[A,X]=\tau (A)X$
,
$[A,X]=\tau (A)X$
, -
(d)
 $[\mathfrak {n}_{-1},\mathfrak {n}_{-2}]=[\mathfrak {n}_{-2},\mathfrak {n}_{-2}]=\{0\}$
,
$[\mathfrak {n}_{-1},\mathfrak {n}_{-2}]=[\mathfrak {n}_{-2},\mathfrak {n}_{-2}]=\{0\}$
, -
(e) and, if
 $X,Y\in \mathfrak {n}_{-1}$
, then
$X,Y\in \mathfrak {n}_{-1}$
, then
 $[X,Y]=\omega (X,Y)$
.
$[X,Y]=\omega (X,Y)$
.
-
-
(3) Moreover, in the case (2), the Lie subalgebra
of
 $\mathfrak {g}_0$
is a 2-step graded Lie algebra, and the algebra
$\mathfrak {g}_0$
is a 2-step graded Lie algebra, and the algebra
 $\mathfrak {n}_{00}$
is a Lie subalgebra of the Lie algebra of all derivations of
$\mathfrak {n}_{00}$
is a Lie subalgebra of the Lie algebra of all derivations of
 preserving its strata
preserving its strata
 $\mathfrak {n}_{-1}$
and
$\mathfrak {n}_{-1}$
and
 $\mathfrak {n}_{-2}$
.
$\mathfrak {n}_{-2}$
.
Remark 2.2. Note that, in the respective bases
![]() $\{ f_\mu \}_{\mu =1}^s$
in S and
$\{ f_\mu \}_{\mu =1}^s$
in S and
![]() $\{e_i\}_{i=1}^r$
in R, the equation (2.1) is
$\{e_i\}_{i=1}^r$
in R, the equation (2.1) is
for all
![]() $A\in \mathfrak {n}_{00}$
, all
$A\in \mathfrak {n}_{00}$
, all
![]() $i=1,2,\dots ,r$
and all
$i=1,2,\dots ,r$
and all
![]() $\mu ,\nu =1,2,\dots ,s$
. On this basis, the condition (1) is
$\mu ,\nu =1,2,\dots ,s$
. On this basis, the condition (1) is
for all
![]() $i=1,2,\dots ,r,\,\mu ,\nu =1,2,\dots s$
, and
$i=1,2,\dots ,r,\,\mu ,\nu =1,2,\dots s$
, and
![]() $A,B\in \mathfrak {n}_{00}$
.
$A,B\in \mathfrak {n}_{00}$
.
Proof of the lemma
The proof of part (1) is a pure calculation using the equation (2.1). We first rewrite it in the shorthand notation as
Then we have
 $$ \begin{align*}\begin{aligned} \tau([A,B]_0)\omega&=\rho([A,B]_0)\omega+\omega\rho([A,B]_0)^T\\ &=\rho(A)\rho(B)\omega-\rho(B)\rho(A)\omega+\omega\rho(B)^T\rho(A)^T-\omega\rho(A)^T\rho(B)^T\\ &=\rho(A)\Big(\tau(B)\omega-\omega\rho(B)^T\Big)-\rho(B)\Big(\tau(A)\omega-\omega\rho(A)^T\Big)\\&\quad +\Big(\tau(B)\omega-\rho(B)\omega\Big)\rho(A)^T-\Big(\tau(A)\omega-\rho(A)\omega\Big)\rho(B)^T\\ &=\rho(A)\Big(\tau(B)\omega\Big)-\rho(B)\Big(\tau(A)\omega\Big)+\Big(\tau(B)\omega\Big)\rho(A)^T-\Big(\tau(A)\omega\Big)\rho(B)^T\\ &= \tau(A)\tau(B)\omega-\tau(B)\omega\rho(A)^T-\Big(\tau(B)\tau(A)\omega-\tau(A)\omega\rho(B)^T\Big)\\ &\quad +\tau(B)\omega\rho(A)^T-\tau(A)\omega\rho(B)^T=\tau(A)\tau(B)\omega-\tau(B)\tau(A)\omega\\ &=([\tau(A,\tau(B)]_{\mathrm{End}(R)})\omega, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \tau([A,B]_0)\omega&=\rho([A,B]_0)\omega+\omega\rho([A,B]_0)^T\\ &=\rho(A)\rho(B)\omega-\rho(B)\rho(A)\omega+\omega\rho(B)^T\rho(A)^T-\omega\rho(A)^T\rho(B)^T\\ &=\rho(A)\Big(\tau(B)\omega-\omega\rho(B)^T\Big)-\rho(B)\Big(\tau(A)\omega-\omega\rho(A)^T\Big)\\&\quad +\Big(\tau(B)\omega-\rho(B)\omega\Big)\rho(A)^T-\Big(\tau(A)\omega-\rho(A)\omega\Big)\rho(B)^T\\ &=\rho(A)\Big(\tau(B)\omega\Big)-\rho(B)\Big(\tau(A)\omega\Big)+\Big(\tau(B)\omega\Big)\rho(A)^T-\Big(\tau(A)\omega\Big)\rho(B)^T\\ &= \tau(A)\tau(B)\omega-\tau(B)\omega\rho(A)^T-\Big(\tau(B)\tau(A)\omega-\tau(A)\omega\rho(B)^T\Big)\\ &\quad +\tau(B)\omega\rho(A)^T-\tau(A)\omega\rho(B)^T=\tau(A)\tau(B)\omega-\tau(B)\tau(A)\omega\\ &=([\tau(A,\tau(B)]_{\mathrm{End}(R)})\omega, \end{aligned} \end{align*} $$
which proves part (1).
The proof of parts (2) and (3) is as follows:
We need to check the Jacobi identity for the bracket
![]() $[\cdot ,\cdot ]$
.
$[\cdot ,\cdot ]$
.
We first consider the representation
defined by
We then prove that the representation
![]() $\sigma $
is a strata preserving derivation in
$\sigma $
is a strata preserving derivation in ![]() . This is implied by the definitions (a)–(e) of the bracket, and the fundamental equation (2.1) as follows:
. This is implied by the definitions (a)–(e) of the bracket, and the fundamental equation (2.1) as follows:
The strata preserving property of
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma (\mathfrak {n}_{-i})\subset \mathfrak {n}_{-i}$
,
$\sigma (\mathfrak {n}_{-i})\subset \mathfrak {n}_{-i}$
,
![]() $i=1,2$
, is obvious by the definitions of
$i=1,2$
, is obvious by the definitions of
![]() $\rho $
and
$\rho $
and
![]() $\tau $
. However, we need to check that
$\tau $
. However, we need to check that
![]() $\sigma $
is a derivation – that is, that
$\sigma $
is a derivation – that is, that
for all
![]() $A\in \mathfrak {n}_{00}$
and for all
$A\in \mathfrak {n}_{00}$
and for all ![]() . Because of the strata preserving property of
. Because of the strata preserving property of
![]() $\sigma $
, which we have just established, and because of the point (d) of the definition of the bracket, the equation (2.3) is satisfied when both X and Y are in
$\sigma $
, which we have just established, and because of the point (d) of the definition of the bracket, the equation (2.3) is satisfied when both X and Y are in
![]() $\mathfrak {n}_{-2}$
, or when X is in
$\mathfrak {n}_{-2}$
, or when X is in
![]() $\mathfrak {n}_{-1}$
and Y is
$\mathfrak {n}_{-1}$
and Y is
![]() $\mathfrak {n}_{-2}$
. The only thing to be checked is if (2.3) is also valid when both X and Y belong to
$\mathfrak {n}_{-2}$
. The only thing to be checked is if (2.3) is also valid when both X and Y belong to
![]() $\mathfrak {n}_{-1}$
. But this just follows directly from (2.1) since if
$\mathfrak {n}_{-1}$
. But this just follows directly from (2.1) since if
![]() $ X,Y\in \mathfrak {n}_{-1}$
, then
$ X,Y\in \mathfrak {n}_{-1}$
, then
 $$ \begin{align*}\begin{aligned}\sigma(A)[X,Y]&=\sigma(A)\omega(X,Y)=\tau(A)\omega(X,Y)=\\ &\omega(\rho(A)X,Y)+\omega(X,\rho(A)Y)=[\rho(A)X,Y]+[X,\rho(A)Y]=\\ &[\sigma(A)X,Y]+[X,\sigma(A)Y],\quad \forall A\in\mathfrak{n}_{00}.\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned}\sigma(A)[X,Y]&=\sigma(A)\omega(X,Y)=\tau(A)\omega(X,Y)=\\ &\omega(\rho(A)X,Y)+\omega(X,\rho(A)Y)=[\rho(A)X,Y]+[X,\rho(A)Y]=\\ &[\sigma(A)X,Y]+[X,\sigma(A)Y],\quad \forall A\in\mathfrak{n}_{00}.\end{aligned}\end{align*} $$
Now we return to checking the Jacobi identity for the bracket
![]() $[\cdot ,\cdot ]$
in
$[\cdot ,\cdot ]$
in
![]() $\mathfrak {g}_0$
:
$\mathfrak {g}_0$
:
On elements of the form
![]() $A,B\in \mathfrak {n}_{00}$
,
$A,B\in \mathfrak {n}_{00}$
, ![]() , by (b)-(c), we have
, by (b)-(c), we have
which vanishes due to the representation property of
![]() $\sigma $
. However, on elements
$\sigma $
. However, on elements
![]() $A\in \mathfrak {n}_{00}$
and
$A\in \mathfrak {n}_{00}$
and ![]() , we have
, we have
which is again zero, on the ground of the derivation property 2.3 of
![]() $\sigma $
. Obviously, the bracket satisfies the Jacobi identity when it is restricted to
$\sigma $
. Obviously, the bracket satisfies the Jacobi identity when it is restricted to
![]() $\mathfrak {n}_{00}$
; it is the Lie bracket
$\mathfrak {n}_{00}$
; it is the Lie bracket
![]() $[\cdot ,\cdot ]_o$
of the Lie algebra
$[\cdot ,\cdot ]_o$
of the Lie algebra
![]() $\mathfrak {n}_{00}$
. Finally, property (2) implies that
$\mathfrak {n}_{00}$
. Finally, property (2) implies that
![]() $[[Z_1,Z_2],Z_3]=0$
for all
$[[Z_1,Z_2],Z_3]=0$
for all
![]() $Z_1,Z_2,Z_3$
in
$Z_1,Z_2,Z_3$
in ![]() ; hence, the Jacobi identity is trivially satisfied for
; hence, the Jacobi identity is trivially satisfied for
![]() $[\cdot ,\cdot ]$
, when it is restricted to
$[\cdot ,\cdot ]$
, when it is restricted to ![]() .
.
In the following, we will use the map
![]() $\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
satisfying the magical equation (2.1) to construct contactifications with nontrivial symmetry algebras
$\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
satisfying the magical equation (2.1) to construct contactifications with nontrivial symmetry algebras
![]() $\mathfrak {g}$
. The setting will include Cartan’s contactification with symmetry
$\mathfrak {g}$
. The setting will include Cartan’s contactification with symmetry
![]() $\mathbf {F}_4$
mentioned in the Helgason’s quote. For this, however, we need few preparations.
$\mathbf {F}_4$
mentioned in the Helgason’s quote. For this, however, we need few preparations.
3. Two-step filtered manifolds
A 2-step filtered structure on an
![]() $(s+r)$
-dimensional manifold M is a pair
$(s+r)$
-dimensional manifold M is a pair
![]() $(M,{\mathcal D})$
, in which
$(M,{\mathcal D})$
, in which
![]() $\mathcal D$
is a vector distribution of rank s on M, such that it is bracket generating in the quickest possible way. This means that its derived distribution
$\mathcal D$
is a vector distribution of rank s on M, such that it is bracket generating in the quickest possible way. This means that its derived distribution
![]() ${\mathcal D}_{-2}:=[{\mathcal D}_{-1},{\mathcal D}_{-1}]$
, with
${\mathcal D}_{-2}:=[{\mathcal D}_{-1},{\mathcal D}_{-1}]$
, with
![]() ${\mathcal D}_{-1}={\mathcal D}$
, is such that
${\mathcal D}_{-1}={\mathcal D}$
, is such that
It provides the simplest nontrivial filtration
of the tangent bundle
![]() $\mathrm {T}M$
.
$\mathrm {T}M$
.
A (local) authomorphism of a 2-step filtered manifold
![]() $(M,{\mathcal D})$
is a (local) diffeomorphism
$(M,{\mathcal D})$
is a (local) diffeomorphism
![]() $\phi :M\to M$
such that
$\phi :M\to M$
such that
![]() $\phi _*{\mathcal D}\subset {\mathcal D}$
. Since authomorphisms can be composed and have inverses, they form a group G of (local) authomorphisms of
$\phi _*{\mathcal D}\subset {\mathcal D}$
. Since authomorphisms can be composed and have inverses, they form a group G of (local) authomorphisms of
![]() $(M,{\mathcal D})$
, also called a group of (local) symmetries of
$(M,{\mathcal D})$
, also called a group of (local) symmetries of
![]() $\mathcal D$
. Infinitesimally, the Lie group of authomorphisms defines the Lie algebra
$\mathcal D$
. Infinitesimally, the Lie group of authomorphisms defines the Lie algebra
![]() $\mathfrak {aut}({\mathcal D})$
of symmetries, which is the real span of all vector fields X on M such that
$\mathfrak {aut}({\mathcal D})$
of symmetries, which is the real span of all vector fields X on M such that
![]() $[X,Y]\subset {\mathcal D}$
for all
$[X,Y]\subset {\mathcal D}$
for all
![]() $Y\in {\mathcal D}$
.
$Y\in {\mathcal D}$
.
Among all the 2-step filtered manifolds
![]() $(M,{\mathcal D})$
particularly simple are those which can be realised on a group manifold of a 2-step nilpotent Lie group. These are related to the notion of the nilpotent approximation of a pair
$(M,{\mathcal D})$
particularly simple are those which can be realised on a group manifold of a 2-step nilpotent Lie group. These are related to the notion of the nilpotent approximation of a pair
![]() $(M,{\mathcal D})$
. This is defined as follows:
$(M,{\mathcal D})$
. This is defined as follows:
At every point
![]() $x\in M$
equipped with a 2-step filtration
$x\in M$
equipped with a 2-step filtration
![]() ${\mathcal D}_{-2}\supset {\mathcal D}_{-1}$
, we have well-defined vector spaces
${\mathcal D}_{-2}\supset {\mathcal D}_{-1}$
, we have well-defined vector spaces
![]() $n_{-1}(x)={\mathcal D}_{-1}(x)$
and
$n_{-1}(x)={\mathcal D}_{-1}(x)$
and
![]() $n_{-2}(x)={\mathcal D}_{-2}(x)/{\mathcal D}_{-1}(x)$
, which define a vector space
$n_{-2}(x)={\mathcal D}_{-2}(x)/{\mathcal D}_{-1}(x)$
, which define a vector space
This vector space is naturally a Lie algebra, with a Lie bracket induced form the Lie bracket of vector fields in
![]() $\mathrm {T}M$
. Due to the 2-step property of the filtration defined by
$\mathrm {T}M$
. Due to the 2-step property of the filtration defined by
![]() $\mathcal D$
, this Lie algebra is 2-step nilpotent,
$\mathcal D$
, this Lie algebra is 2-step nilpotent,
This 2-step nilpotent Lie algebra is a local invariant of the structure
![]() $(M,{\mathcal D})$
, and it is called a nilpotent approximation of the structure
$(M,{\mathcal D})$
, and it is called a nilpotent approximation of the structure
![]() $(M,{\mathcal D})$
at
$(M,{\mathcal D})$
at
![]() $x\in M$
.
$x\in M$
.
This enables for defining a class of particularly simple examples of 2-step filtered structures:
Consider a 2-step nilpotent Lie algebra
![]() $\mathfrak {n}=\mathfrak {n}_{-2}\oplus \mathfrak {n}_{-1}$
, and let M be a Lie group, whose Lie algebra is
$\mathfrak {n}=\mathfrak {n}_{-2}\oplus \mathfrak {n}_{-1}$
, and let M be a Lie group, whose Lie algebra is
![]() $\mathfrak {n}$
. The Lie algebra
$\mathfrak {n}$
. The Lie algebra
![]() $\mathfrak {n}_M$
of left invariant vector fields on M is isomorphic to
$\mathfrak {n}_M$
of left invariant vector fields on M is isomorphic to
![]() $\mathfrak {n}$
and mirrors its gradation,
$\mathfrak {n}$
and mirrors its gradation,
![]() $\mathfrak {n}_M={\mathfrak {n}_M}_{-2}\oplus {\mathfrak {n}_M}_{-1}$
. Now, taking all linear combinations with smooth functions coefficients of all vector fields from the graded component
$\mathfrak {n}_M={\mathfrak {n}_M}_{-2}\oplus {\mathfrak {n}_M}_{-1}$
. Now, taking all linear combinations with smooth functions coefficients of all vector fields from the graded component
![]() ${\mathfrak {n}_M}_{-1}$
of
${\mathfrak {n}_M}_{-1}$
of
![]() $\mathfrak {n}_M$
, one defines a vector distribution
$\mathfrak {n}_M$
, one defines a vector distribution
![]() ${\mathcal D}=\mathrm {Span}_{{\mathcal {F}}(M)}(\mathfrak {n}_M)$
on M. The so constructed filtered structure
${\mathcal D}=\mathrm {Span}_{{\mathcal {F}}(M)}(\mathfrak {n}_M)$
on M. The so constructed filtered structure
![]() $(M,{\mathcal D})$
is obviously 2-step graded and is the simplest filtered structure with nilpotent approximation being equal to
$(M,{\mathcal D})$
is obviously 2-step graded and is the simplest filtered structure with nilpotent approximation being equal to
![]() $\mathfrak {n}$
everywhere. We call this
$\mathfrak {n}$
everywhere. We call this
![]() $(M,{\mathcal D})$
structure the flat model for all the 2-step filtered structures having the same constant nilpotent approximation
$(M,{\mathcal D})$
structure the flat model for all the 2-step filtered structures having the same constant nilpotent approximation
![]() $\mathfrak {n}$
.
$\mathfrak {n}$
.
It is remarkable that the largest possible symmetry of all 2-step filtered structures
![]() $(M,{\mathcal D})$
is precisely the symmetry of the flat model. As such, it is algebraically determined by the nilpotent approximation
$(M,{\mathcal D})$
is precisely the symmetry of the flat model. As such, it is algebraically determined by the nilpotent approximation
![]() $\mathfrak {n}$
. This is the result of Noboru Tanaka [Reference Tanaka18]. To describe it, we recall the notion of Tanaka prolongation.
$\mathfrak {n}$
. This is the result of Noboru Tanaka [Reference Tanaka18]. To describe it, we recall the notion of Tanaka prolongation.
Definition 3.1. The Tanaka prolongation of a 2-step nilpotent Lie algebra
![]() $\mathfrak {n}$
is a graded Lie algebra
$\mathfrak {n}$
is a graded Lie algebra
![]() $\mathfrak {g}(\mathfrak {n})$
given by a direct sum
$\mathfrak {g}(\mathfrak {n})$
given by a direct sum
with
 $$ \begin{align}\mathfrak{n}_k=\Big\{\bigoplus_{j<0}\mathfrak{n}_{k+j}\otimes\mathfrak{n}_j^*\ni A\,\,\mathrm{s.t.}\,\,A[X,Y]=[AX,Y]+[X,AY]\Big\}\end{align} $$
$$ \begin{align}\mathfrak{n}_k=\Big\{\bigoplus_{j<0}\mathfrak{n}_{k+j}\otimes\mathfrak{n}_j^*\ni A\,\,\mathrm{s.t.}\,\,A[X,Y]=[AX,Y]+[X,AY]\Big\}\end{align} $$
for each
![]() $k\geq 0$
.
$k\geq 0$
.
Furthermore, for each
![]() $j\geq 0$
, the Lie algebra
$j\geq 0$
, the Lie algebra
is called the Tanaka prolongations of
![]() $\mathfrak {n}$
up to
$\mathfrak {n}$
up to
![]() $j^{th}$
order.
$j^{th}$
order.
Setting
![]() $[A,X]=AX$
for all
$[A,X]=AX$
for all
![]() $A\in \mathfrak {n}_k$
with
$A\in \mathfrak {n}_k$
with
![]() $k\geq 0$
and for all
$k\geq 0$
and for all
![]() $X\in \mathfrak {n}$
makes the condition in (3.2) into the Jacobi identity. Moreover, if
$X\in \mathfrak {n}$
makes the condition in (3.2) into the Jacobi identity. Moreover, if
![]() $A\in \mathfrak {n}_k$
and
$A\in \mathfrak {n}_k$
and
![]() $B\in \mathfrak {n}_l$
,
$B\in \mathfrak {n}_l$
,
![]() $k,l\geq 0$
, then their commutator
$k,l\geq 0$
, then their commutator
![]() $[A,B]\in \mathfrak {n}_{k+l}$
is defined on elements
$[A,B]\in \mathfrak {n}_{k+l}$
is defined on elements
![]() $X\in \mathfrak {n}$
inductively, according to the Jacobi identity. By this, we mean that it should satisfy
$X\in \mathfrak {n}$
inductively, according to the Jacobi identity. By this, we mean that it should satisfy
which is sufficient enough to define
![]() $[A,B]$
.
$[A,B]$
.
Remark 3.2. Note, in particular, that
![]() $\mathfrak {n}_0$
is the Lie algebra of all derivations of
$\mathfrak {n}_0$
is the Lie algebra of all derivations of
![]() $\mathfrak {n}$
preserving the two strata
$\mathfrak {n}$
preserving the two strata
![]() $\mathfrak {n}_{-1}$
and
$\mathfrak {n}_{-1}$
and
![]() $\mathfrak {n}_{-2}$
of the direct sum
$\mathfrak {n}_{-2}$
of the direct sum
![]() $\mathfrak {n}=\mathfrak {n}_{-2}\oplus \mathfrak {n}_{-1}$
:
$\mathfrak {n}=\mathfrak {n}_{-2}\oplus \mathfrak {n}_{-1}$
:
Although the Tanaka prolongation of a nilpotent Lie algebra
![]() $\mathfrak {n}$
is in general infinite, in this paper, we will be interested in situations when the Tanaka prolongation
$\mathfrak {n}$
is in general infinite, in this paper, we will be interested in situations when the Tanaka prolongation
of the
![]() $2$
-step nilpotent part
$2$
-step nilpotent part
is finite and symmetric, in the sense
with
Such situations are possible, and in them the so defined Lie algebra
![]() $\mathfrak {g}(\mathfrak {n})$
is simple. In such a case, the Tanaka prolongation
$\mathfrak {g}(\mathfrak {n})$
is simple. In such a case, the Tanaka prolongation
![]() $\mathfrak {g}(\mathfrak {n})$
is graded, and the subalgebra
$\mathfrak {g}(\mathfrak {n})$
is graded, and the subalgebra
in such
![]() $\mathfrak {g}(\mathfrak {n})$
is parabolic. Moreover, the Lie algebra
$\mathfrak {g}(\mathfrak {n})$
is parabolic. Moreover, the Lie algebra
is also a parabolic subalgebra of this simple
![]() $\mathfrak {g}(\mathfrak {n})$
. It is isomorphic to
$\mathfrak {g}(\mathfrak {n})$
. It is isomorphic to
![]() $\mathfrak {p}$
,
$\mathfrak {p}$
,
![]() $\mathfrak {p}\simeq \mathfrak {p}_{opp}$
.
$\mathfrak {p}\simeq \mathfrak {p}_{opp}$
.
Regardless of whether
![]() $\mathfrak {g}(\mathfrak {n})$
is finite or not, we have the following general theorem, which is a specialisation of a remarkable theorem by Noboru Tanaka [Reference Tanaka18]:
$\mathfrak {g}(\mathfrak {n})$
is finite or not, we have the following general theorem, which is a specialisation of a remarkable theorem by Noboru Tanaka [Reference Tanaka18]:
Theorem 3.3. Consider 2-step filtered structures
![]() $(M,{\mathcal D})$
, with distributions
$(M,{\mathcal D})$
, with distributions
![]() ${\mathcal D}$
having the same constant nilpotent approximation
${\mathcal D}$
having the same constant nilpotent approximation
![]() $\mathfrak {n}$
. Then
$\mathfrak {n}$
. Then
-
• The most symmetric of all of these distribution structures is the flat model
 $(M,{\mathcal D})$
, with M being a nilpotent Lie group associated of the nilpotent approximation algebra
$(M,{\mathcal D})$
, with M being a nilpotent Lie group associated of the nilpotent approximation algebra
 $\mathfrak {n}$
, and with
$\mathfrak {n}$
, and with
 $\mathcal D$
being the first component
$\mathcal D$
being the first component
 ${\mathcal D}^{-1}$
of the natural filtration on M associated to the
${\mathcal D}^{-1}$
of the natural filtration on M associated to the
 $2$
-step grading in
$2$
-step grading in
 $\mathfrak {n}$
.
$\mathfrak {n}$
. -
• The Lie algebra of authomorphism
 $\mathfrak {aut}({\mathcal D})$
of the flat model structure is isomorphic to the Tanaka prolongation
$\mathfrak {aut}({\mathcal D})$
of the flat model structure is isomorphic to the Tanaka prolongation
 $\mathfrak {g}(\mathfrak {n})$
of the nilpotent approximation
$\mathfrak {g}(\mathfrak {n})$
of the nilpotent approximation
 $\mathfrak {n}$
,
$\mathfrak {n}$
,
 $\mathfrak {aut}({\mathcal D})\simeq \mathfrak {g}(\mathfrak {n}).$
$\mathfrak {aut}({\mathcal D})\simeq \mathfrak {g}(\mathfrak {n}).$
Remark 3.4. This theorem is of fundamental importance for explanation of the Cartan’s result about a realisation of
![]() $\mathbf {F}_4$
in
$\mathbf {F}_4$
in
![]() $\mathbb {R}^{15}$
. As we will see, Cartan’s
$\mathbb {R}^{15}$
. As we will see, Cartan’s
![]() $\mathbb {R}^{15}$
is actually a domain of a chart
$\mathbb {R}^{15}$
is actually a domain of a chart
![]() $({\mathcal U},\varphi )$
on a certain 2-step nilpotent Lie group M, with a 2-step nilpotent Lie algebra
$({\mathcal U},\varphi )$
on a certain 2-step nilpotent Lie group M, with a 2-step nilpotent Lie algebra
![]() $\mathfrak {n}$
, and the equivalent description of
$\mathfrak {n}$
, and the equivalent description of
![]() $\mathbf {F}_4$
in terms of a symmetry group of the contactification
$\mathbf {F}_4$
in terms of a symmetry group of the contactification
![]() $(M,{\mathcal D})$
from our Example 1.3 is valid because this contactification is just the flat model for the 2-step filtration
$(M,{\mathcal D})$
from our Example 1.3 is valid because this contactification is just the flat model for the 2-step filtration
![]() $(M,{\mathcal D})$
with the nilpotent approximation
$(M,{\mathcal D})$
with the nilpotent approximation
![]() $\mathfrak {n}$
.
$\mathfrak {n}$
.
Using the information about the Tanaka prolongation of a nilpotent Lie algebra
![]() $\mathfrak {n}$
, we can enlarge our Lemma 2.1 by changing its point (3) into the following more complete form:
$\mathfrak {n}$
, we can enlarge our Lemma 2.1 by changing its point (3) into the following more complete form:
Lemma 3.5. With all the assumptions of Lemma 2.1, and with points (1) and (2) as in Lemma 2.1, its point (3) is equivalent to the following:
-
(3) Moreover, in the case (2), the Lie subalgebra
of is a 2-step graded nilpotent Lie algebra, and the algebra
is a 2-step graded nilpotent Lie algebra, and the algebra $$ \begin{align*}\mathfrak{g}_0=\mathfrak{n}_{-2}\oplus\mathfrak{n}_{-1}\oplus \mathfrak{n}_{00}\end{align*} $$
$$ \begin{align*}\mathfrak{g}_0=\mathfrak{n}_{-2}\oplus\mathfrak{n}_{-1}\oplus \mathfrak{n}_{00}\end{align*} $$
 $\mathfrak {n}_{00}$
is a Lie subalgebra of the Tanaka prolongation up to
$\mathfrak {n}_{00}$
is a Lie subalgebra of the Tanaka prolongation up to
 $0^{th}$
order
$0^{th}$
order  of the Lie algebra
of the Lie algebra  .
.
Remark 3.6. The term ‘...
![]() $\mathfrak {n}_{00}$
is a Lie subalgebra of the Tanaka prolongation up to
$\mathfrak {n}_{00}$
is a Lie subalgebra of the Tanaka prolongation up to
![]() $0^{th}$
order
$0^{th}$
order ![]() of the Lie algebra
of the Lie algebra ![]() ..’ in the above lemma means that
..’ in the above lemma means that
![]() $\mathfrak {n}_{00}$
, although nontrivial, is in general only a subalgebra of the
$\mathfrak {n}_{00}$
, although nontrivial, is in general only a subalgebra of the
which is the full
![]() $0$
graded component of the Tanaka prolongation of
$0$
graded component of the Tanaka prolongation of ![]() . So for applications, it is reasonable to choose
. So for applications, it is reasonable to choose
![]() $\mathfrak {n}_{00}$
as large as possible.
$\mathfrak {n}_{00}$
as large as possible.
4. Construction of contactifications with nice symmetries
Consider a Lie algebra
![]() $(\mathfrak {n}_{00},[\cdot ,\cdot ]_0)$
and its two real representations
$(\mathfrak {n}_{00},[\cdot ,\cdot ]_0)$
and its two real representations
![]() $(\rho ,S)$
,
$(\rho ,S)$
,
![]() $(\tau ,R)$
, in the respective real s- and r-dimensional vector spaces S and R. Let
$(\tau ,R)$
, in the respective real s- and r-dimensional vector spaces S and R. Let
![]() $S=\mathbb {R}^s$
,
$S=\mathbb {R}^s$
,
![]() $R=\mathbb {R}^r$
, and let
$R=\mathbb {R}^r$
, and let
![]() $\{ f_\mu \}_{\mu =1}^s$
and
$\{ f_\mu \}_{\mu =1}^s$
and
![]() $\{e_i\}_{i=1}^r$
be respective bases in S and in R. Let
$\{e_i\}_{i=1}^r$
be respective bases in S and in R. Let
![]() $\{f^\mu \}_{\mu =1}^s$
be a basis in the vector space
$\{f^\mu \}_{\mu =1}^s$
be a basis in the vector space
![]() $S^*$
dual to the basis
$S^*$
dual to the basis
![]() $\{ f_\mu \}_{\mu =1}^s$
,
$\{ f_\mu \}_{\mu =1}^s$
, ![]() . To be in a situation of Lemma 2.1, we also assume that we have the homomorphism
. To be in a situation of Lemma 2.1, we also assume that we have the homomorphism
![]() $\omega \in \mathrm {Hom}(\bigwedge ^2 S,R)$
satisfying the magical equation (2.1).
$\omega \in \mathrm {Hom}(\bigwedge ^2 S,R)$
satisfying the magical equation (2.1).
Then the map
![]() $\omega $
is
$\omega $
is
and it defines the coefficients
![]() $\omega ^i{}_{\mu \nu }$
,
$\omega ^i{}_{\mu \nu }$
,
![]() $i=1,\dots ,r$
,
$i=1,\dots ,r$
,
![]() $\mu ,\nu =1,2,\dots s$
, which satisfy
$\mu ,\nu =1,2,\dots s$
, which satisfy
![]() $\omega ^i{}_{\mu \nu }=-\omega ^i{}_{\nu \mu }$
.
$\omega ^i{}_{\mu \nu }=-\omega ^i{}_{\nu \mu }$
.
Now, consider an s-dimensional manifold, which is an open set N of
![]() $\mathbb {R}^s$
,
$\mathbb {R}^s$
,
![]() $N\subset \mathbb {R}^s$
, with coordinates
$N\subset \mathbb {R}^s$
, with coordinates
![]() $(x^\mu )_{\mu =1}^r$
. Then we have r two-forms
$(x^\mu )_{\mu =1}^r$
. Then we have r two-forms
![]() $(\omega ^i)_{i=1}^r$
on N, defined by
$(\omega ^i)_{i=1}^r$
on N, defined by
This produces an
![]() $(N,\mathrm {d}{\mathcal D}^\perp )$
structure on N, with
$(N,\mathrm {d}{\mathcal D}^\perp )$
structure on N, with
We contactify it. For this, we take a local
![]() $M=\mathbb {R}^r\times N$
, with coordinates
$M=\mathbb {R}^r\times N$
, with coordinates
![]() $\big (u^i,x^\mu \big )\phantom {}_{i=1}^r\phantom {}_{\mu =1}^s$
, and define the ‘contact forms’ on M by
$\big (u^i,x^\mu \big )\phantom {}_{i=1}^r\phantom {}_{\mu =1}^s$
, and define the ‘contact forms’ on M by
Because of Lemmas 2.1 and 3.5, the distribution
![]() ${\mathcal D}$
on M defined by this contactification as in Definition 1.1 equips M with a 2-step filtered structure having
${\mathcal D}$
on M defined by this contactification as in Definition 1.1 equips M with a 2-step filtered structure having
![]() ${\mathcal D}_{-1}=\mathcal D$
. This has rank s. Now using Lemmas 2.1 and 3.5, and Tanaka’s Theorem 3.3, we get the following corollary.
${\mathcal D}_{-1}=\mathcal D$
. This has rank s. Now using Lemmas 2.1 and 3.5, and Tanaka’s Theorem 3.3, we get the following corollary.
Corollary 4.1. Let
![]() $M=\mathbb {R}^r\times \mathbb {R}^s$
and let
$M=\mathbb {R}^r\times \mathbb {R}^s$
and let
with
![]() $\omega $
being a solution of the magical equation 2.1 such that
$\omega $
being a solution of the magical equation 2.1 such that
![]() $\mathrm {Im}(\omega )=R$
. Consider the distribution structure
$\mathrm {Im}(\omega )=R$
. Consider the distribution structure
![]() $(M,{\mathcal D})$
with a rank r distribution
$(M,{\mathcal D})$
with a rank r distribution
on M. Then the Lie algebra of authomorphism
![]() $\mathfrak {aut}({\mathcal D})$
of
$\mathfrak {aut}({\mathcal D})$
of
![]() $(M,{\mathcal D})$
is isomorphic to the Tanaka prolongation of the 2-step nilpotent Lie algebra
$(M,{\mathcal D})$
is isomorphic to the Tanaka prolongation of the 2-step nilpotent Lie algebra ![]() defined in point (3) of Lemma 2.1 or 3.5. The Lie algebra
defined in point (3) of Lemma 2.1 or 3.5. The Lie algebra
![]() $\mathfrak {g}_0=R\oplus S\oplus \mathfrak {n}_{00}$
is nontrivially contained in the Tanaka prolongation up to the
$\mathfrak {g}_0=R\oplus S\oplus \mathfrak {n}_{00}$
is nontrivially contained in the Tanaka prolongation up to the
![]() $0^{th}$
order
$0^{th}$
order ![]() of
of ![]() , with
, with
![]() $\{0\}\neq \mathfrak {n}_{00}\subset \mathfrak {n}_0$
, and as such is a subalgebra of the algebra of
$\{0\}\neq \mathfrak {n}_{00}\subset \mathfrak {n}_0$
, and as such is a subalgebra of the algebra of
![]() $\mathfrak {aut}({\mathcal D})$
.
$\mathfrak {aut}({\mathcal D})$
.
5. Majorana spinor representations of
 $\mathfrak {so}(p,q)$
$\mathfrak {so}(p,q)$
In this section, we will explain how to construct the real spin representations of the Lie algebras
![]() $\mathfrak {so}(p,q)$
, in cases when
$\mathfrak {so}(p,q)$
, in cases when
![]() $p=n$
,
$p=n$
,
![]() $q=n-1$
, or
$q=n-1$
, or
![]() $p=q=n$
,
$p=q=n$
,
![]() $n=1,2,\dots n$
. We will also give a construction of these representations for
$n=1,2,\dots n$
. We will also give a construction of these representations for
![]() $\mathfrak {so}(0,n)$
. We emphasise that we are only interested in real spin representations. They share a general name of Majorana representations. Our presentation of this material is adapted from [Reference Trautman, Naber, Tsou and Françoise19].
$\mathfrak {so}(0,n)$
. We emphasise that we are only interested in real spin representations. They share a general name of Majorana representations. Our presentation of this material is adapted from [Reference Trautman, Naber, Tsou and Françoise19].
We will need Pauli matrices
 $$ \begin{align} \sigma_x=\begin{pmatrix} 0&1\\1&0\end{pmatrix},\quad \epsilon=-i\sigma_y=\begin{pmatrix} 0&-1\\1&0\end{pmatrix},\quad \sigma_z=\begin{pmatrix} 1&0\\0&-1\end{pmatrix} \end{align} $$
$$ \begin{align} \sigma_x=\begin{pmatrix} 0&1\\1&0\end{pmatrix},\quad \epsilon=-i\sigma_y=\begin{pmatrix} 0&-1\\1&0\end{pmatrix},\quad \sigma_z=\begin{pmatrix} 1&0\\0&-1\end{pmatrix} \end{align} $$
and the
![]() $2\times 2$
identity matrix
$2\times 2$
identity matrix
 $$ \begin{align} I=\begin{pmatrix} 1&0\\0&1\end{pmatrix}.\end{align} $$
$$ \begin{align} I=\begin{pmatrix} 1&0\\0&1\end{pmatrix}.\end{align} $$
We have the following identities:
 $$ \begin{align}\begin{aligned} &\sigma_x^2=\sigma_z^2=-\epsilon^2=I\\ &\sigma_x\epsilon=-\epsilon\sigma_x=\sigma_z,\quad\sigma_z\sigma_x=-\sigma_x\sigma_z=-\epsilon,\quad \epsilon\sigma_z=-\sigma_z\epsilon=\sigma_x. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} &\sigma_x^2=\sigma_z^2=-\epsilon^2=I\\ &\sigma_x\epsilon=-\epsilon\sigma_x=\sigma_z,\quad\sigma_z\sigma_x=-\sigma_x\sigma_z=-\epsilon,\quad \epsilon\sigma_z=-\sigma_z\epsilon=\sigma_x. \end{aligned} \end{align} $$
Now we quote [Reference Trautman, Naber, Tsou and Françoise19]:
With this notation, restricting to low dimensions
![]() $p+q=4,5,6$
and
$p+q=4,5,6$
and
![]() $7$
, the real representations of the Clifford algebra
$7$
, the real representations of the Clifford algebra
![]() ${\mathcal C}\ell (0,p+q)$
are all in dimension
${\mathcal C}\ell (0,p+q)$
are all in dimension
![]() $s=8$
, and are generated by the
$s=8$
, and are generated by the
![]() $p+q$
matrices
$p+q$
matrices
![]() $\rho _1,\dots ,\rho _{(p+q)}$
given by:
$\rho _1,\dots ,\rho _{(p+q)}$
given by:
 $$ \begin{align}\begin{aligned} \rho_1&=\sigma_z\otimes I\otimes \epsilon\\ \rho_2&=\sigma_z\otimes \epsilon\otimes \sigma_x\\ \rho_3&=\sigma_z\otimes \epsilon\otimes \sigma_z\\ \rho_4&=\sigma_x\otimes \epsilon \otimes I\\ \rho_5&=\sigma_x\otimes \sigma_x\otimes \epsilon\\ \rho_6&=\sigma_x\otimes \sigma_z\otimes \epsilon\\ \rho_7&=\epsilon\otimes I\otimes I. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \rho_1&=\sigma_z\otimes I\otimes \epsilon\\ \rho_2&=\sigma_z\otimes \epsilon\otimes \sigma_x\\ \rho_3&=\sigma_z\otimes \epsilon\otimes \sigma_z\\ \rho_4&=\sigma_x\otimes \epsilon \otimes I\\ \rho_5&=\sigma_x\otimes \sigma_x\otimes \epsilon\\ \rho_6&=\sigma_x\otimes \sigma_z\otimes \epsilon\\ \rho_7&=\epsilon\otimes I\otimes I. \end{aligned}\end{align} $$
The eight matrices
![]() $\theta _\mu =\sigma _x\otimes \rho _\mu $
,
$\theta _\mu =\sigma _x\otimes \rho _\mu $
,
![]() $\mu =1,\dots , 7$
and
$\mu =1,\dots , 7$
and
![]() $\theta _8=\epsilon \otimes I \otimes I\otimes I$
, give the real representation of
$\theta _8=\epsilon \otimes I \otimes I\otimes I$
, give the real representation of
![]() ${\mathcal C}\ell (0,8)$
in
${\mathcal C}\ell (0,8)$
in
![]() $S=\mathbb {R}^{16}$
. Dropping the first factor in
$S=\mathbb {R}^{16}$
. Dropping the first factor in
![]() $\rho _1,\rho _2,\rho _3$
one obtains the matrices generating a representation of
$\rho _1,\rho _2,\rho _3$
one obtains the matrices generating a representation of
![]() ${\mathcal C}\ell (0,3)$
in
${\mathcal C}\ell (0,3)$
in
![]() $S=\mathbb {R}^4$
, etc.
$S=\mathbb {R}^4$
, etc.
Majorana representations of
![]() $\mathfrak {so}(n-1,n)$
in dimension
$\mathfrak {so}(n-1,n)$
in dimension
![]() $s=2^{n-1}$
are called Pauli representations, and Majorana representations of
$s=2^{n-1}$
are called Pauli representations, and Majorana representations of
![]() $\mathfrak {so}(n,n)$
in dimension
$\mathfrak {so}(n,n)$
in dimension
![]() $s=2^n$
are called Dirac representations.
$s=2^n$
are called Dirac representations.
To construct them, we need generalisations of the Pauli
![]() $\sigma $
matrices and Dirac
$\sigma $
matrices and Dirac
![]() $\gamma $
matrices. The construction of those is inductive.
$\gamma $
matrices. The construction of those is inductive.
It starts with
![]() $p+q=1$
with one matrix
$p+q=1$
with one matrix
![]() $\sigma _1=1$
, and for every
$\sigma _1=1$
, and for every
![]() $n=1,2,\dots $
, it alternates between
$n=1,2,\dots $
, it alternates between
![]() $p+q=2n-1$
of Pauli matrices
$p+q=2n-1$
of Pauli matrices
![]() $\sigma _\mu $
,
$\sigma _\mu $
,
![]() $\mu =1,\dots , 2n-1$
, and
$\mu =1,\dots , 2n-1$
, and
![]() $p+q=2n$
of Dirac matrices
$p+q=2n$
of Dirac matrices
![]() $\gamma _\mu $
,
$\gamma _\mu $
,
![]() $\mu =1,\dots , 2n$
.
$\mu =1,\dots , 2n$
.
Again quoting Trautman [Reference Trautman, Naber, Tsou and Françoise19] we have the following:
-
(1) In dimension
 $p+q=1$
, put
$p+q=1$
, put
 $\sigma _1=1$
.
$\sigma _1=1$
. -
(2) Given
 $2^{n-1}\times 2^{n-1}$
matrices
$2^{n-1}\times 2^{n-1}$
matrices
 $\sigma _\mu $
,
$\sigma _\mu $
,
 $\mu =1,\dots ,2n-1$
, define and
$\mu =1,\dots ,2n-1$
, define and $$ \begin{align*}\gamma_\mu=\begin{pmatrix} 0&\sigma_\mu\\\sigma_\mu&0\end{pmatrix}\,\,\mathrm{for}\,\,\mu=1,\dots,2n-1,\end{align*} $$
where I is the identity
$$ \begin{align*}\gamma_\mu=\begin{pmatrix} 0&\sigma_\mu\\\sigma_\mu&0\end{pmatrix}\,\,\mathrm{for}\,\,\mu=1,\dots,2n-1,\end{align*} $$
where I is the identity $$ \begin{align*}\gamma_{2n}=\begin{pmatrix} 0&-I\\I&0\end{pmatrix},\end{align*} $$
$$ \begin{align*}\gamma_{2n}=\begin{pmatrix} 0&-I\\I&0\end{pmatrix},\end{align*} $$
 $2^{n-1}\times 2^{n-1}$
matrix.
$2^{n-1}\times 2^{n-1}$
matrix.
-
(3) Given
 $2^n\times 2^n$
matrices
$2^n\times 2^n$
matrices
 $\gamma _\mu $
,
$\gamma _\mu $
,
 $\mu =1,\dots ,2n$
, define
$\mu =1,\dots ,2n$
, define
 $\sigma _\mu =\gamma _\mu $
for
$\sigma _\mu =\gamma _\mu $
for
 $\mu =1,\dots , 2n$
and
$\mu =1,\dots , 2n$
and
 $\sigma _{2n+1}=\gamma _1\dots \gamma _{2n}$
, so that for
$\sigma _{2n+1}=\gamma _1\dots \gamma _{2n}$
, so that for
 $n>0$
,
$n>0$
,  $$ \begin{align*}\sigma_{2n+1}=\begin{pmatrix} I&0\\0&-I\end{pmatrix}.\end{align*} $$
$$ \begin{align*}\sigma_{2n+1}=\begin{pmatrix} I&0\\0&-I\end{pmatrix}.\end{align*} $$
In every dimension
![]() $p+q=2n-1$
,
$p+q=2n-1$
,
![]() $n\geq 1$
, the Pauli matrices
$n\geq 1$
, the Pauli matrices
![]() $\sigma _\mu $
,
$\sigma _\mu $
,
![]() $\mu =1,\dots ,2n-1$
satisfy
$\mu =1,\dots ,2n-1$
satisfy
 $$ \begin{align*}\sigma_\mu\sigma_\nu+\sigma_\nu\sigma_\mu=2g_{\mu\nu}\underbrace{\big(I\otimes\dots\otimes I\big)}_{n-1\,\, \mathrm{times}},\end{align*} $$
$$ \begin{align*}\sigma_\mu\sigma_\nu+\sigma_\nu\sigma_\mu=2g_{\mu\nu}\underbrace{\big(I\otimes\dots\otimes I\big)}_{n-1\,\, \mathrm{times}},\end{align*} $$
where the
![]() $(2n-1)\times (2n-1)$
symmetric matrix
$(2n-1)\times (2n-1)$
symmetric matrix
![]() $(g_{\mu \nu })$
is diagonal and has the following diagonal elements:
$(g_{\mu \nu })$
is diagonal and has the following diagonal elements:
 $$ \begin{align*}(g_{\mu\nu})=\mathrm{diag}\underbrace{(1,-1,\dots,-1,1)}_{(2n-1)\,\, \mathrm{times}}.\end{align*} $$
$$ \begin{align*}(g_{\mu\nu})=\mathrm{diag}\underbrace{(1,-1,\dots,-1,1)}_{(2n-1)\,\, \mathrm{times}}.\end{align*} $$
Likewise, in every dimension
![]() $p+q=2n$
,
$p+q=2n$
,
![]() $n\geq 1$
, the Dirac matrices
$n\geq 1$
, the Dirac matrices
![]() $\gamma _\mu $
,
$\gamma _\mu $
,
![]() $\mu =1,\dots ,2n$
satisfy
$\mu =1,\dots ,2n$
satisfy
 $$ \begin{align*}\gamma_\mu\gamma_\nu+\gamma_\nu\gamma_\mu=2g_{\mu\nu}\underbrace{\big(I\otimes\dots\otimes I\big)}_{n\,\, \mathrm{times}},\end{align*} $$
$$ \begin{align*}\gamma_\mu\gamma_\nu+\gamma_\nu\gamma_\mu=2g_{\mu\nu}\underbrace{\big(I\otimes\dots\otimes I\big)}_{n\,\, \mathrm{times}},\end{align*} $$
where the
![]() $(2n)\times (2n)$
symmetric matrix
$(2n)\times (2n)$
symmetric matrix
![]() $(g_{\mu \nu })$
is diagonal and has the following diagonal elements:
$(g_{\mu \nu })$
is diagonal and has the following diagonal elements:
Therefore, for each
![]() $n=1,2,\dots $
, the set
$n=1,2,\dots $
, the set
![]() $\{\sigma _\mu \}_{\mu =1}^{2n-1}$
of Pauli matrices generates the elements of a real
$\{\sigma _\mu \}_{\mu =1}^{2n-1}$
of Pauli matrices generates the elements of a real
![]() $2^{n-1}$
-dimensional representation of the Clifford algebra
$2^{n-1}$
-dimensional representation of the Clifford algebra
![]() ${\mathcal C}\ell (n-1,n)$
, and the set
${\mathcal C}\ell (n-1,n)$
, and the set
![]() $\{\gamma _\mu \}_{\mu =1}^{2n}$
of Dirac matrices generates the elements of a real
$\{\gamma _\mu \}_{\mu =1}^{2n}$
of Dirac matrices generates the elements of a real
![]() $2^{n}$
-dimensional representation of the Clifford algebra
$2^{n}$
-dimensional representation of the Clifford algebra
![]() ${\mathcal C}\ell (n,n)$
.
${\mathcal C}\ell (n,n)$
.
Then, in turn, these real Clifford algebras representations can be further used to define the real spin representations of the Lie algebras
![]() $\mathfrak {so}(p+q,0)$
,
$\mathfrak {so}(p+q,0)$
,
![]() $\mathfrak {so}(n-1,n)$
and
$\mathfrak {so}(n-1,n)$
and
![]() $\mathfrak {so}(n,n)$
as follows. One obtains all the generators of the spin representation of
$\mathfrak {so}(n,n)$
as follows. One obtains all the generators of the spin representation of
![]() $\mathfrak {so}(g)$
by spanning it by all the elements of the form
$\mathfrak {so}(g)$
by spanning it by all the elements of the form
-
•
 $\tfrac 12\rho _\mu \rho _\nu $
, with
$\tfrac 12\rho _\mu \rho _\nu $
, with
 $1\leq \mu <\nu \leq (p+q)$
, in the case of
$1\leq \mu <\nu \leq (p+q)$
, in the case of
 $\mathfrak {so}(p+q,0)$
,
$\mathfrak {so}(p+q,0)$
,
 $p+q=3,5,6,7$
;
$p+q=3,5,6,7$
; -
•
 $\tfrac 12\theta _\mu \theta _\nu $
, with
$\tfrac 12\theta _\mu \theta _\nu $
, with
 $1\leq \mu <\nu \leq 8$
, in the case of
$1\leq \mu <\nu \leq 8$
, in the case of
 $\mathfrak {so}(8,0)$
;
$\mathfrak {so}(8,0)$
; -
•
 $\tfrac 12\sigma _\mu \sigma _\nu $
, with
$\tfrac 12\sigma _\mu \sigma _\nu $
, with
 $1\leq \mu <\nu \leq (p+q)=2n-1$
, in the case of
$1\leq \mu <\nu \leq (p+q)=2n-1$
, in the case of
 $\mathfrak {so}(n-1,n)$
;
$\mathfrak {so}(n-1,n)$
; -
•
 $\tfrac 12\gamma _\mu \gamma _\nu $
, with
$\tfrac 12\gamma _\mu \gamma _\nu $
, with
 $1\leq \mu <\nu \leq (p+q)=2n$
, in the case of
$1\leq \mu <\nu \leq (p+q)=2n$
, in the case of
 $\mathfrak {so}(n,n)$
.
$\mathfrak {so}(n,n)$
.
For further details, consult [Reference Trautman, Naber, Tsou and Françoise19].
We will use all this information in next sections when we create examples.
6. Application: Obtaining the flat model for (3,6) distributions
Let
![]() $(\rho ,S)$
be the defining representation of
$(\rho ,S)$
be the defining representation of
![]() $\mathfrak {so}(3)$
in
$\mathfrak {so}(3)$
in
![]() $S=\mathbb {R}^3$
. It can be generated by
$S=\mathbb {R}^3$
. It can be generated by
 $$ \begin{align}\rho(A_1)=\begin{pmatrix} 0&0&-1\\0&0&0\\1&0&0\end{pmatrix},\quad\rho(A_2)=\begin{pmatrix} 0&1&0\\-1&0&0\\0&0&0\end{pmatrix},\quad\rho(A_1)=\begin{pmatrix} 0&0&0\\0&0&-1\\0&1&0\end{pmatrix}.\end{align} $$
$$ \begin{align}\rho(A_1)=\begin{pmatrix} 0&0&-1\\0&0&0\\1&0&0\end{pmatrix},\quad\rho(A_2)=\begin{pmatrix} 0&1&0\\-1&0&0\\0&0&0\end{pmatrix},\quad\rho(A_1)=\begin{pmatrix} 0&0&0\\0&0&-1\\0&1&0\end{pmatrix}.\end{align} $$
And let
![]() $(\tau ,R)$
be an equivalent 3-dimensional representation of
$(\tau ,R)$
be an equivalent 3-dimensional representation of
![]() $\mathfrak {so}(3)$
given by
$\mathfrak {so}(3)$
given by
 $$ \begin{align} \tau(A_1)=\begin{pmatrix} 0&0&-1\\0&0&0\\1&0&0\end{pmatrix},\quad\tau(A_2)=\begin{pmatrix} 0&-1&0\\1&0&0\\0&0&0\end{pmatrix},\quad\tau(A_1)=\begin{pmatrix} 0&0&0\\0&0&1\\0&-1&0\end{pmatrix}.\end{align} $$
$$ \begin{align} \tau(A_1)=\begin{pmatrix} 0&0&-1\\0&0&0\\1&0&0\end{pmatrix},\quad\tau(A_2)=\begin{pmatrix} 0&-1&0\\1&0&0\\0&0&0\end{pmatrix},\quad\tau(A_1)=\begin{pmatrix} 0&0&0\\0&0&1\\0&-1&0\end{pmatrix}.\end{align} $$
We claim that for these two representations of
![]() $\mathfrak {so}(3)$
, in the standard bases in
$\mathfrak {so}(3)$
, in the standard bases in
![]() $S=\mathbb {R}^3$
,
$S=\mathbb {R}^3$
,
![]() $R=\mathbb {R}^3$
, the magical equation (2.2) has the following solution:
$R=\mathbb {R}^3$
, the magical equation (2.2) has the following solution:
 $$ \begin{align*}\omega^1{}_{\mu\nu}=\begin{pmatrix} 0&0&0\\0&0&-1\\0&1&0\end{pmatrix},\quad\omega^2{}_{\mu\nu}=\begin{pmatrix} 0&0&-1\\0&0&0\\1&0&0\end{pmatrix},\quad\omega^3{}_{\mu\nu}=\begin{pmatrix} 0&-1&0\\1&0&0\\0&0&0\end{pmatrix}.\end{align*} $$
$$ \begin{align*}\omega^1{}_{\mu\nu}=\begin{pmatrix} 0&0&0\\0&0&-1\\0&1&0\end{pmatrix},\quad\omega^2{}_{\mu\nu}=\begin{pmatrix} 0&0&-1\\0&0&0\\1&0&0\end{pmatrix},\quad\omega^3{}_{\mu\nu}=\begin{pmatrix} 0&-1&0\\1&0&0\\0&0&0\end{pmatrix}.\end{align*} $$
Now using this solution
![]() $(\rho ,\tau ,\omega )$
of the magical equation (2.1), we use the Corollary 4.1 with
$(\rho ,\tau ,\omega )$
of the magical equation (2.1), we use the Corollary 4.1 with
![]() $\lambda ^i=\mathrm {d} u^u+\omega ^i{}_{\mu \nu }x^\mu \mathrm {d} x^\nu $
and obtain the following theorem.
$\lambda ^i=\mathrm {d} u^u+\omega ^i{}_{\mu \nu }x^\mu \mathrm {d} x^\nu $
and obtain the following theorem.
Theorem 6.1. Let
![]() $M=\mathbb {R}^6$
with coordinates
$M=\mathbb {R}^6$
with coordinates
![]() $(u^1,u^2,u^3,x^1,x^2,x^3)$
and consider three 1-forms
$(u^1,u^2,u^3,x^1,x^2,x^3)$
and consider three 1-forms
 $$ \begin{align*}\begin{aligned} \lambda^1& =\mathrm{d} u^1+x^2\mathrm{d} x^3\\ \lambda^2& =\mathrm{d} u^2+x^1\mathrm{d} x^3\\ \lambda^3& =\mathrm{d} u^3+x^1\mathrm{d} x^2 \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1& =\mathrm{d} u^1+x^2\mathrm{d} x^3\\ \lambda^2& =\mathrm{d} u^2+x^1\mathrm{d} x^3\\ \lambda^3& =\mathrm{d} u^3+x^1\mathrm{d} x^2 \end{aligned}\end{align*} $$
on M. Then the rank 3 distribution
![]() ${\mathcal D}$
on M defined by
${\mathcal D}$
on M defined by ![]() has its Lie algebra of infinitesimal symmetries
has its Lie algebra of infinitesimal symmetries
![]() $\mathfrak {aut}{\mathcal D}$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}{\mathcal D}$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^3)$
and
$(\rho ,S=\mathbb {R}^3)$
and
![]() $(\tau ,R=\mathbb {R}^3)$
are the respective representations (6.1), (6.2) of
$(\tau ,R=\mathbb {R}^3)$
are the respective representations (6.1), (6.2) of
![]() $\mathfrak {n}_{00}=\mathfrak {so}(3)$
.
$\mathfrak {n}_{00}=\mathfrak {so}(3)$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple graded Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple graded Lie algebra
![]() $\mathfrak {so}(4,3)$
,
$\mathfrak {so}(4,3)$
,
with the following gradation:
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S$
,
$\mathfrak {n}_{-1}=S$
,
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
$\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {so}(4,3)$
.
$\mathfrak {so}(4,3)$
.
The contactification
![]() $(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
![]() $\big (\mathbf {Spin}(4,3),P\big )$
related to the following crossed Satake diagram:
$\big (\mathbf {Spin}(4,3),P\big )$
related to the following crossed Satake diagram: ![]() .
.
Proof. Proof is by calculating the Tanaka prolongation of ![]() , which is
, which is
![]() $\mathfrak {gl}(3,\mathbb {R})$
, naturally graded by the Tanaka prolongation algebraic procedure precisely as
$\mathfrak {gl}(3,\mathbb {R})$
, naturally graded by the Tanaka prolongation algebraic procedure precisely as
![]() $\mathfrak {aut}({\mathcal D})$
in the statement of the theorem.
$\mathfrak {aut}({\mathcal D})$
in the statement of the theorem.
7. Application: Obtaining Biquard’s 7-dimensional flat quaternionic contact manifold via contactification using spin representations of
 $\mathfrak {so}(1,2)$
and
$\mathfrak {so}(1,2)$
and
 $\mathfrak {so}(3,0)$
$\mathfrak {so}(3,0)$
According to Trautman’s procedure, [Reference Trautman, Naber, Tsou and Françoise19] there is a real representation of
![]() ${\mathcal C}\ell (0,3)$
in
${\mathcal C}\ell (0,3)$
in
![]() $\mathbb {R}^4$
. There also is an analogous representation of
$\mathbb {R}^4$
. There also is an analogous representation of
![]() ${\mathcal C}\ell (1,2)$
. Both of them are generated by the
${\mathcal C}\ell (1,2)$
. Both of them are generated by the
![]() $\sigma $
matrices
$\sigma $
matrices
 $$ \begin{align*}\sigma_1=\begin{pmatrix} 0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{pmatrix},\quad\sigma_2=\begin{pmatrix} 0&0&0&-\varepsilon\\0&0&-\varepsilon&0\\0&1&0&0\\1&0&0&0\end{pmatrix},\quad\sigma_3=\begin{pmatrix} 0&0&-\varepsilon&0\\0&0&0&\varepsilon\\1&0&0&0\\0&-1&0&0\end{pmatrix},\end{align*} $$
$$ \begin{align*}\sigma_1=\begin{pmatrix} 0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{pmatrix},\quad\sigma_2=\begin{pmatrix} 0&0&0&-\varepsilon\\0&0&-\varepsilon&0\\0&1&0&0\\1&0&0&0\end{pmatrix},\quad\sigma_3=\begin{pmatrix} 0&0&-\varepsilon&0\\0&0&0&\varepsilon\\1&0&0&0\\0&-1&0&0\end{pmatrix},\end{align*} $$
where
and
One can check that these matricesFootnote 1 satisfy the (representation of) Clifford algebra relations:
with all
![]() $g_{\mu \nu }$
being zero, except
$g_{\mu \nu }$
being zero, except
![]() $g_{11}=-1$
,
$g_{11}=-1$
,
![]() $g_{22}=g_{33}=-\varepsilon $
.
$g_{22}=g_{33}=-\varepsilon $
.
This leads to the following spinorial representation
![]() $\rho $
of
$\rho $
of
![]() $\mathfrak {so}(0,3)$
or
$\mathfrak {so}(0,3)$
or
![]() $\mathfrak {so}(1,2)$
:
$\mathfrak {so}(1,2)$
:
Here,
![]() $(A_1,A_2,A_3)$
constitutes a basis for
$(A_1,A_2,A_3)$
constitutes a basis for
![]() $\mathfrak {so}(0,3)$
when
$\mathfrak {so}(0,3)$
when
![]() $\varepsilon =1$
and for
$\varepsilon =1$
and for
![]() $\mathfrak {so}(2,1)$
when
$\mathfrak {so}(2,1)$
when
![]() $\varepsilon =-1$
. This can be extended to the representation of
$\varepsilon =-1$
. This can be extended to the representation of
in
![]() $S=\mathbb {R}^4$
by setting the value of
$S=\mathbb {R}^4$
by setting the value of
![]() $\rho $
on the generator
$\rho $
on the generator
![]() $A_4=\mathrm {Id}$
as
$A_4=\mathrm {Id}$
as
For this representation of
![]() $\mathbb {R}\oplus \mathfrak {so}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
, the magical equation (2.1) has a following solution:
$\mathbb {R}\oplus \mathfrak {so}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
, the magical equation (2.1) has a following solution:
 $$ \begin{align*}\begin{aligned} \omega^1{}_{\mu\nu}=&\begin{pmatrix} 0&0&1&0\\0&0&0&-1\\-1&0&0&0\\0&1&0&0\end{pmatrix},\quad \omega^2{}_{\mu\nu}=\begin{pmatrix} 0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{pmatrix},\\ &\\ &\omega^1{}_{\mu\nu}=\begin{pmatrix} 0&-\varepsilon&0&0\\\varepsilon&0&0&0\\0&0&0&-1\\0&0&1&0\end{pmatrix}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \omega^1{}_{\mu\nu}=&\begin{pmatrix} 0&0&1&0\\0&0&0&-1\\-1&0&0&0\\0&1&0&0\end{pmatrix},\quad \omega^2{}_{\mu\nu}=\begin{pmatrix} 0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{pmatrix},\\ &\\ &\omega^1{}_{\mu\nu}=\begin{pmatrix} 0&-\varepsilon&0&0\\\varepsilon&0&0&0\\0&0&0&-1\\0&0&1&0\end{pmatrix}, \end{aligned}\end{align*} $$
with
 $$ \begin{align}\begin{aligned} \tau(A_1)=\begin{pmatrix} 0&0&0\\0&0&\varepsilon\\0&-1&0\end{pmatrix},\quad &\tau(A_2)=\begin{pmatrix} 0&0&-\varepsilon\\0&0&0\\-1&0&0\end{pmatrix},\quad\tau(A_3)=\begin{pmatrix} 0&-\varepsilon&0\\\varepsilon&0&0\\0&0&0\end{pmatrix}\\ &\tau(A_4)=\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1\end{pmatrix}. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \tau(A_1)=\begin{pmatrix} 0&0&0\\0&0&\varepsilon\\0&-1&0\end{pmatrix},\quad &\tau(A_2)=\begin{pmatrix} 0&0&-\varepsilon\\0&0&0\\-1&0&0\end{pmatrix},\quad\tau(A_3)=\begin{pmatrix} 0&-\varepsilon&0\\\varepsilon&0&0\\0&0&0\end{pmatrix}\\ &\tau(A_4)=\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1\end{pmatrix}. \end{aligned} \end{align} $$
This in particular gives the vectorial representation
![]() $\tau $
of
$\tau $
of
in
![]() $R=\mathbb {R}^3$
.
$R=\mathbb {R}^3$
.
Now, by using this solution for
![]() $(\rho ,\omega ,\tau )$
and applying our Corollary 4.1, we have an
$(\rho ,\omega ,\tau )$
and applying our Corollary 4.1, we have an
![]() $(s=4)$
-dimensional manifold
$(s=4)$
-dimensional manifold
![]() $N=\mathbb {R}^4$
, equipped with
$N=\mathbb {R}^4$
, equipped with
![]() $r=3$
two-forms
$r=3$
two-forms
![]() $\omega ^i=\tfrac 12\omega ^{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
,
$\omega ^i=\tfrac 12\omega ^{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
,
![]() $i=1,2,3$
, which contactifies to an
$i=1,2,3$
, which contactifies to an
![]() $(s+r)=7$
-dimensional manifold
$(s+r)=7$
-dimensional manifold
![]() $M=\mathbb {R}^7$
having a distribution structure
$M=\mathbb {R}^7$
having a distribution structure
![]() $(M,{\mathcal D})$
defined as an annihilator of the
$(M,{\mathcal D})$
defined as an annihilator of the
![]() $r=3$
one-forms
$r=3$
one-forms
![]() $\lambda ^i=\mathrm {d} u^i+\omega ^i{}_{\mu \nu }x^\mu \mathrm {d} x^\nu $
,
$\lambda ^i=\mathrm {d} u^i+\omega ^i{}_{\mu \nu }x^\mu \mathrm {d} x^\nu $
,
![]() $i=1,2,3$
. We have the following theorem.
$i=1,2,3$
. We have the following theorem.
Theorem 7.1. Let
![]() $M=\mathbb {R}^7$
with coordinates
$M=\mathbb {R}^7$
with coordinates
![]() $(u^1,u^2,u^3,x^1,x^2,x^3,x^4)$
, and consider three 1-forms
$(u^1,u^2,u^3,x^1,x^2,x^3,x^4)$
, and consider three 1-forms
![]() $\lambda ^1,\lambda ^2,\lambda ^3$
on M given by
$\lambda ^1,\lambda ^2,\lambda ^3$
on M given by
 $$ \begin{align*}\begin{aligned} \lambda^1=&\mathrm{d} u^1+x^1\mathrm{d} x^3-x^2\mathrm{d} x^4,\\ \lambda^2=&\mathrm{d} u^2-x^1\mathrm{d} x^4-x^2\mathrm{d} x^3,\\ \lambda^3=&\mathrm{d} u^3-\varepsilon x^1\mathrm{d} x^2-x^3\mathrm{d} x^4, \end{aligned}\quad\quad\mathrm{with}\quad\quad\varepsilon=\pm1.\end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1=&\mathrm{d} u^1+x^1\mathrm{d} x^3-x^2\mathrm{d} x^4,\\ \lambda^2=&\mathrm{d} u^2-x^1\mathrm{d} x^4-x^2\mathrm{d} x^3,\\ \lambda^3=&\mathrm{d} u^3-\varepsilon x^1\mathrm{d} x^2-x^3\mathrm{d} x^4, \end{aligned}\quad\quad\mathrm{with}\quad\quad\varepsilon=\pm1.\end{align*} $$
The rank 4 distribution
![]() ${\mathcal D}$
on M defined as
${\mathcal D}$
on M defined as ![]() has its Lie algebra of infinitesimal authomorphism
has its Lie algebra of infinitesimal authomorphism
![]() $\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^4)$
is the spinorial representation (7.1)-(7.2) of
$(\rho ,S=\mathbb {R}^4)$
is the spinorial representation (7.1)-(7.2) of
![]() $\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
, and
$\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
, and
![]() $(\tau ,R=\mathbb {R}^3)$
is the vectorial representation (7.3) of
$(\tau ,R=\mathbb {R}^3)$
is the vectorial representation (7.3) of
![]() $\mathfrak {n}_{00}$
.
$\mathfrak {n}_{00}$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple Lie algebra
![]() $\mathfrak {sp}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
,
$\mathfrak {sp}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
,
having the following natural gradation:
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S$
,
$\mathfrak {n}_{-1}=S$
,
 $$ \begin{align*}\begin{aligned} \mathfrak{n}_0&=\mathfrak{n}_{00}\oplus \mathfrak{so}\big(\tfrac{1-\varepsilon}{2},\tfrac{5+\varepsilon}{2}\big)=\\&\mathbb{R}\oplus \mathfrak{so}\big(\tfrac{1-\varepsilon}{2},\tfrac{5+\varepsilon}{2}\big)\oplus \mathfrak{so}\big(\tfrac{1-\varepsilon}{2},\tfrac{5+\varepsilon}{2}\big),\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \mathfrak{n}_0&=\mathfrak{n}_{00}\oplus \mathfrak{so}\big(\tfrac{1-\varepsilon}{2},\tfrac{5+\varepsilon}{2}\big)=\\&\mathbb{R}\oplus \mathfrak{so}\big(\tfrac{1-\varepsilon}{2},\tfrac{5+\varepsilon}{2}\big)\oplus \mathfrak{so}\big(\tfrac{1-\varepsilon}{2},\tfrac{5+\varepsilon}{2}\big),\end{aligned}\end{align*} $$
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
$\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {sp}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
.
$\mathfrak {sp}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big )$
.
The contactification
![]() $(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
![]() $\Big (\mathbf {Sp}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big ),P\Big )$
related to the following crossed satake diagrams:
$\Big (\mathbf {Sp}\big (\tfrac {1-\varepsilon }{2},\tfrac {5+\varepsilon }{2}\big ),P\Big )$
related to the following crossed satake diagrams:
-
(1)
 in the case of
in the case of
 $\varepsilon =1$
, and
$\varepsilon =1$
, and -
(2)
 in the case of
in the case of
 $\varepsilon =-1$
.
$\varepsilon =-1$
.
Remark 7.2. When
![]() $\varepsilon =1$
, the flat parabolic geometry described in the above theorem is the lowest dimensional example of the quaternionic contact geometry considered by Biquard [Reference Biquard5] (see also [Reference Duchemin12]).
$\varepsilon =1$
, the flat parabolic geometry described in the above theorem is the lowest dimensional example of the quaternionic contact geometry considered by Biquard [Reference Biquard5] (see also [Reference Duchemin12]).
8. Application: Obtaining the exceptionals from contactifications of spin representations; the
 $\mathfrak {f}_4$
case
$\mathfrak {f}_4$
case
We will now explain the Cartan realisation of the simple exceptional Lie algebra
![]() $\mathfrak {f}_4$
in dimension
$\mathfrak {f}_4$
in dimension
![]() $\mathbb {R}^{15}$
mentioned in the introduction.
$\mathbb {R}^{15}$
mentioned in the introduction.
The Satake diagrams for the real forms of the complex simple exceptional Lie algebra
![]() $\mathfrak {f}_4$
are as follows:
$\mathfrak {f}_4$
are as follows:
The first diagram corresponds to the compact real form of
![]() $\mathfrak {f}_4$
and is not interesting for us.Footnote
2
The other two diagrams are interesting:
$\mathfrak {f}_4$
and is not interesting for us.Footnote
2
The other two diagrams are interesting:
-
(1) The last,
 , corresponds to the split real form
, corresponds to the split real form
 $\mathfrak {f}_I$
, and
$\mathfrak {f}_I$
, and -
(2) the middle one,
 , denoted by
, denoted by
 $\mathfrak {f}_{II}$
in [Reference Čap and Slovák11], is also interesting, since similarly to
$\mathfrak {f}_{II}$
in [Reference Čap and Slovák11], is also interesting, since similarly to
 $\mathfrak {f}_I$
, it defines a parabolic geometry in dimension 15.
$\mathfrak {f}_I$
, it defines a parabolic geometry in dimension 15.
Crossing the last node on the right in the diagrams for
![]() $\mathfrak {f}_I$
or
$\mathfrak {f}_I$
or
![]() $\mathfrak {f}_{II}$
, as in
$\mathfrak {f}_{II}$
, as in ![]() or
or ![]() , we see that in both algebras there exist parabolic subalgebras
, we see that in both algebras there exist parabolic subalgebras
![]() $\mathfrak {p}_I$
or
$\mathfrak {p}_I$
or
![]() $\mathfrak {p}_{II}$
, respectively, of dimension 37,
$\mathfrak {p}_{II}$
, respectively, of dimension 37,
![]() $\dim (\mathfrak {p}_I)=\dim (\mathfrak {p}_{II})=37$
. In both respective cases, these choices of parabolics define similar gradations in the corresponding real forms
$\dim (\mathfrak {p}_I)=\dim (\mathfrak {p}_{II})=37$
. In both respective cases, these choices of parabolics define similar gradations in the corresponding real forms
![]() $\mathfrak {f}_I$
,
$\mathfrak {f}_I$
,
![]() $\mathfrak {f}_{II}$
, of the simple exceptional Lie
$\mathfrak {f}_{II}$
, of the simple exceptional Lie
![]() $\mathfrak {f}_4$
:
$\mathfrak {f}_4$
:
with
being 2-step nilpotent and having grading components
![]() $\mathfrak {n}_{-2A}$
and
$\mathfrak {n}_{-2A}$
and
![]() $\mathfrak {n}_{-1A}$
of respective dimension
$\mathfrak {n}_{-1A}$
of respective dimension
![]() $r_A=7$
and
$r_A=7$
and
![]() $s_A=8$
,
$s_A=8$
,
The Lie algebra
![]() $\mathfrak {n}_{0A}$
in the Tanaka prolongation of
$\mathfrak {n}_{0A}$
in the Tanaka prolongation of
![]() $\mathfrak {n}_{-A}$
up to
$\mathfrak {n}_{-A}$
up to
![]() $0^{th}$
order is
$0^{th}$
order is
-
(1)
 $\mathfrak {n}_{0I}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the case of
$\mathfrak {n}_{0I}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the case of
 $\mathfrak {f}_I$
, and
$\mathfrak {f}_I$
, and -
(2)
 $\mathfrak {n}_{0II}=\mathbb {R}\oplus \mathfrak {so}(0,7)$
in the case of
$\mathfrak {n}_{0II}=\mathbb {R}\oplus \mathfrak {so}(0,7)$
in the case of
 $\mathfrak {f}_{II}$
.
$\mathfrak {f}_{II}$
.
Thus, from the analysis performed here, we see that there exist two different 2-step filtered structures
![]() $(M_I,{\mathcal D}_I)$
and
$(M_I,{\mathcal D}_I)$
and
![]() $(M_{II},{\mathcal D}_{II})$
, both in dimension 15, with the respective
$(M_{II},{\mathcal D}_{II})$
, both in dimension 15, with the respective
![]() $F_I$
-symmetric, or
$F_I$
-symmetric, or
![]() $F_{II}$
-symmetric flat models, realised on
$F_{II}$
-symmetric flat models, realised on
![]() $M_I=F_I/P_I$
or
$M_I=F_I/P_I$
or
![]() $M_{II}=F_{II}/P_{II}$
. Here,
$M_{II}=F_{II}/P_{II}$
. Here,
![]() $F_I$
and
$F_I$
and
![]() $F_{II}$
denote the real Lie groups whose Lie algebras are
$F_{II}$
denote the real Lie groups whose Lie algebras are
![]() $\mathfrak {f}_I$
and
$\mathfrak {f}_I$
and
![]() $\mathfrak {f}_{II}$
, respectively. Similarly,
$\mathfrak {f}_{II}$
, respectively. Similarly,
![]() $P_I$
and
$P_I$
and
![]() $P_{II}$
are parabolic subgroups of respective
$P_{II}$
are parabolic subgroups of respective
![]() $F_I$
and
$F_I$
and
![]() $F_{II}$
, whose Lie algebras are
$F_{II}$
, whose Lie algebras are
![]() $\mathfrak {p}_I$
and
$\mathfrak {p}_I$
and
![]() $\mathfrak {p}_{II}$
. Recalling that each of the real groups
$\mathfrak {p}_{II}$
. Recalling that each of the real groups
![]() $\mathbf {SO}(4,3)$
and
$\mathbf {SO}(4,3)$
and
![]() $\mathbf {SO}(0,7)$
has two real irreducible representations
$\mathbf {SO}(0,7)$
has two real irreducible representations
![]() $\rho $
in dimension
$\rho $
in dimension
![]() $s=8$
and
$s=8$
and
![]() $\tau $
in dimension
$\tau $
in dimension
![]() $r=7$
, with the 8-dimensional representation
$r=7$
, with the 8-dimensional representation
![]() $\rho $
being the spin representation of either
$\rho $
being the spin representation of either
![]() $\mathbf {SO}(4,3)$
or
$\mathbf {SO}(4,3)$
or
![]() $\mathbf {SO}(0,7)$
, we can now give the explicit realisations of the
$\mathbf {SO}(0,7)$
, we can now give the explicit realisations of the
![]() $\mathbf {F}_4$
-symmetric structures
$\mathbf {F}_4$
-symmetric structures
![]() $(M_A,{\mathcal D}_A)$
for
$(M_A,{\mathcal D}_A)$
for
![]() $A=I,II$
.
$A=I,II$
.
8.1. Cartan’s realisation of
 $\mathfrak {f}_I$
$\mathfrak {f}_I$
The plan is to start with the Lie algebra
![]() $\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
, as in the crossed Satake diagram
$\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
, as in the crossed Satake diagram ![]() of
of
![]() $\mathfrak {f}_I$
, and its two representations:
$\mathfrak {f}_I$
, and its two representations:
-
• a representaion
 $(\rho ,S=\mathbb {R}^8)$
, corresponding to the spin representation of
$(\rho ,S=\mathbb {R}^8)$
, corresponding to the spin representation of
 $\mathbf {SO}(4,3)$
in
$\mathbf {SO}(4,3)$
in
 $(s=8)$
-dimensional space
$(s=8)$
-dimensional space
 $\mathfrak {n}_{-1}=S$
of real Pauli spinors, and
$\mathfrak {n}_{-1}=S$
of real Pauli spinors, and -
• a representation
 $(\tau ,R=\mathbb {R}^7)$
, corresponding to the vectorial representation of
$(\tau ,R=\mathbb {R}^7)$
, corresponding to the vectorial representation of
 $\mathbf {SO}(4,3)$
in
$\mathbf {SO}(4,3)$
in
 $(r=7)$
-dimensional space
$(r=7)$
-dimensional space
 $\mathfrak {n}_{-2}=R$
of vectors in
$\mathfrak {n}_{-2}=R$
of vectors in
 $\mathbb {R}^{(4,3)}$
.
$\mathbb {R}^{(4,3)}$
.
Having these two representations of
![]() $\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the same basis, we will then solve the equations (2.1) for the map
$\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the same basis, we will then solve the equations (2.1) for the map
![]() $\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
, which will give us the commutators between elements in
$\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
, which will give us the commutators between elements in
![]() $\mathfrak {n}_{-1}$
. This via Corollary 4.1 will provide the explicit realisation of the 15-dimensional contactification
$\mathfrak {n}_{-1}$
. This via Corollary 4.1 will provide the explicit realisation of the 15-dimensional contactification
![]() $(M,{\mathcal D})$
with the exception of simple Lie algebra
$(M,{\mathcal D})$
with the exception of simple Lie algebra
![]() $F_I$
as its symmetry.
$F_I$
as its symmetry.
Actually, the passage from
![]() $\rho $
to
$\rho $
to
![]() $\tau $
in the above plan is a bit tricky, since we need to have these representations expressed in the same basis. To handle this obstacle, we will start with the spin representation
$\tau $
in the above plan is a bit tricky, since we need to have these representations expressed in the same basis. To handle this obstacle, we will start with the spin representation
![]() $\rho $
in the space of Pauli spinors S, and then we will use the fact that the skew representation
$\rho $
in the space of Pauli spinors S, and then we will use the fact that the skew representation
![]() $\rho \wedge \rho $
in the space of the bispinors
$\rho \wedge \rho $
in the space of the bispinors
![]() $\bigwedge ^2S$
decomposes as
$\bigwedge ^2S$
decomposes as
where
![]() $\bigwedge _{21}$
is the 21-dimensional adjoint representation of
$\bigwedge _{21}$
is the 21-dimensional adjoint representation of
![]() $\mathbf {SO}(4,3)$
and
$\mathbf {SO}(4,3)$
and
![]() $\bigwedge _7$
is its 7-dimensional vectorial representation
$\bigwedge _7$
is its 7-dimensional vectorial representation
![]() $\tau $
. In this way, we will have the two representations
$\tau $
. In this way, we will have the two representations
![]() $(\rho ,S)$
and
$(\rho ,S)$
and
![]() $(\tau ,R=\bigwedge _7)$
, expressed in the same basis
$(\tau ,R=\bigwedge _7)$
, expressed in the same basis
![]() $\{A_I\}$
of
$\{A_I\}$
of
![]() $\mathbb {R}\oplus \mathbf {SO}(4,3)$
, and we will apply the Corollary 4.1 to get the desired
$\mathbb {R}\oplus \mathbf {SO}(4,3)$
, and we will apply the Corollary 4.1 to get the desired
![]() $F_I$
-symmetric contactification in dimension 15. On doing this, we will use notation from Section 5.
$F_I$
-symmetric contactification in dimension 15. On doing this, we will use notation from Section 5.
According to [Reference Trautman, Naber, Tsou and Françoise19], the real 8-dimensional representation of the Clifford algebra
![]() ${\mathcal C}\ell (4,3)$
is generated by the seven 8-dimensional Pauli matrices:
${\mathcal C}\ell (4,3)$
is generated by the seven 8-dimensional Pauli matrices:
 $$ \begin{align*}\begin{aligned} &\sigma_1=\sigma_x\otimes\sigma_x\otimes\sigma_x\\ &\sigma_2=\sigma_x\otimes\sigma_x\otimes\epsilon\\ &\sigma_3=\sigma_x\otimes\sigma_x\otimes\sigma_z\\ &\sigma_4=\sigma_x\otimes\epsilon\otimes I\\ &\sigma_5=\sigma_x\otimes\sigma_z\otimes I\\ &\sigma_6=\epsilon\otimes I\otimes I\\ &\sigma_7=\sigma_z\otimes I\otimes I. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\sigma_1=\sigma_x\otimes\sigma_x\otimes\sigma_x\\ &\sigma_2=\sigma_x\otimes\sigma_x\otimes\epsilon\\ &\sigma_3=\sigma_x\otimes\sigma_x\otimes\sigma_z\\ &\sigma_4=\sigma_x\otimes\epsilon\otimes I\\ &\sigma_5=\sigma_x\otimes\sigma_z\otimes I\\ &\sigma_6=\epsilon\otimes I\otimes I\\ &\sigma_7=\sigma_z\otimes I\otimes I. \end{aligned} \end{align*} $$
Using the identities (5.3), especially the one saying that
![]() $\epsilon ^2=-I$
, one easily finds that the seven Pauli matrices
$\epsilon ^2=-I$
, one easily finds that the seven Pauli matrices
![]() $\sigma _i$
,
$\sigma _i$
,
![]() $i=1,2,\dots ,7$
, satisfy the Clifford algebra identity
$i=1,2,\dots ,7$
, satisfy the Clifford algebra identity
with the coefficients
![]() $g_{ij}$
forming a diagonal
$g_{ij}$
forming a diagonal
![]() $7\times 7$
matrix
$7\times 7$
matrix
of signature
![]() $(4,3)$
. Thus, the 8-dimensional Pauli matrices
$(4,3)$
. Thus, the 8-dimensional Pauli matrices
![]() $\sigma _i$
,
$\sigma _i$
,
![]() $i=1,\dots ,7$
generate the Clifford algebra
$i=1,\dots ,7$
generate the Clifford algebra
![]() ${\mathcal C}\ell (4,3)$
, and in turn, by the general theory, as described in Section 5, they define the spin representation
${\mathcal C}\ell (4,3)$
, and in turn, by the general theory, as described in Section 5, they define the spin representation
![]() $\rho $
of
$\rho $
of
![]() $\mathfrak {so}(4,3)$
in an 8-dimensional real vector space
$\mathfrak {so}(4,3)$
in an 8-dimensional real vector space
![]() $S=\mathbb {R}^8$
of Pauli(-Majorana) spinors.
$S=\mathbb {R}^8$
of Pauli(-Majorana) spinors.
8.1.1/ The spinorial representation of
 $\mathfrak {so}(4,3)$
$\mathfrak {so}(4,3)$
To be more explicit, let
![]() $(i,j)$
be such that
$(i,j)$
be such that
![]() $1\leq i<j\leq 7$
, and let I be a function
$1\leq i<j\leq 7$
, and let I be a function
on such pairs. Note that the function I is a bijection between the 21 pairs
![]() $(i,j)$
and the set of 21 natural numbers
$(i,j)$
and the set of 21 natural numbers
![]() $I=1,2,\dots , 21$
. Consider the twenty-one
$I=1,2,\dots , 21$
. Consider the twenty-one
![]() $8\times 8$
real matrices
$8\times 8$
real matrices
![]() $\sigma _i\sigma _j$
with
$\sigma _i\sigma _j$
with
![]() $1\leq i<j\leq 7$
, and a basis
$1\leq i<j\leq 7$
, and a basis
![]() $\{A_I\}_{I=1}^{21}$
in the Lie algebra
$\{A_I\}_{I=1}^{21}$
in the Lie algebra
![]() $\mathfrak {so}(4,3)$
. Then the spin representation
$\mathfrak {so}(4,3)$
. Then the spin representation
![]() $\rho $
of
$\rho $
of
![]() $\mathfrak {so}(4,3)$
is given by
$\mathfrak {so}(4,3)$
is given by
Explicitly, we have
 $$ \begin{align} \begin{array}{lll} \rho(A_1)=\tfrac12 I\otimes I \otimes\sigma_z,&\quad \rho(A_8)=\tfrac12 I\otimes \epsilon\otimes\epsilon,&\quad \rho(A_{15})=\tfrac12 \sigma_z\otimes \sigma_z \otimes I,\\ \rho(A_2)=\tfrac12 I\otimes I \otimes\epsilon, &\quad\rho(A_9)=\tfrac12 I\otimes \epsilon \otimes\sigma_z, &\quad \rho(A_{16})=\tfrac12 \epsilon\otimes \sigma_x \otimes\sigma_x, \\ \rho(A_3)=\tfrac12 I\otimes I \otimes\sigma_x, &\quad\rho(A_{10})=\tfrac12 I\otimes \sigma_x \otimes I,&\quad \rho(A_{17})=\tfrac12 \epsilon\otimes \sigma_x \otimes\epsilon,\\ \rho(A_4)=\tfrac12 I\otimes I \otimes\sigma_x,&\quad \rho(A_{11})=\tfrac12 \sigma_z\otimes \sigma_x \otimes\sigma_x,&\quad \rho(A_{18})=\tfrac12 \epsilon\otimes \sigma_x \otimes\sigma_z,\\ \rho(A_5)=\tfrac12 I\otimes \sigma_z \otimes\epsilon,&\quad \rho(A_{12})=\tfrac12 \sigma_z\otimes \sigma_x \otimes\epsilon,&\quad \rho(A_{19})=\tfrac12 \epsilon\otimes \epsilon \otimes I,\\ \rho(A_6)=\tfrac12 I\otimes \sigma_z \otimes\sigma_z,&\quad \rho(A_{13})=\tfrac12 \sigma_z\otimes \sigma_x\otimes\sigma_z,&\quad \rho(A_{20})=\tfrac12 \epsilon\otimes \sigma_z \otimes I,\\ \rho(A_7)=\tfrac12 I\otimes \epsilon \otimes\sigma_x, &\quad \rho(A_{14})=\tfrac12 \sigma_z\otimes \epsilon\otimes I, &\quad \rho(A_{21})=\tfrac12 \sigma_x\otimes I \otimes I. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{lll} \rho(A_1)=\tfrac12 I\otimes I \otimes\sigma_z,&\quad \rho(A_8)=\tfrac12 I\otimes \epsilon\otimes\epsilon,&\quad \rho(A_{15})=\tfrac12 \sigma_z\otimes \sigma_z \otimes I,\\ \rho(A_2)=\tfrac12 I\otimes I \otimes\epsilon, &\quad\rho(A_9)=\tfrac12 I\otimes \epsilon \otimes\sigma_z, &\quad \rho(A_{16})=\tfrac12 \epsilon\otimes \sigma_x \otimes\sigma_x, \\ \rho(A_3)=\tfrac12 I\otimes I \otimes\sigma_x, &\quad\rho(A_{10})=\tfrac12 I\otimes \sigma_x \otimes I,&\quad \rho(A_{17})=\tfrac12 \epsilon\otimes \sigma_x \otimes\epsilon,\\ \rho(A_4)=\tfrac12 I\otimes I \otimes\sigma_x,&\quad \rho(A_{11})=\tfrac12 \sigma_z\otimes \sigma_x \otimes\sigma_x,&\quad \rho(A_{18})=\tfrac12 \epsilon\otimes \sigma_x \otimes\sigma_z,\\ \rho(A_5)=\tfrac12 I\otimes \sigma_z \otimes\epsilon,&\quad \rho(A_{12})=\tfrac12 \sigma_z\otimes \sigma_x \otimes\epsilon,&\quad \rho(A_{19})=\tfrac12 \epsilon\otimes \epsilon \otimes I,\\ \rho(A_6)=\tfrac12 I\otimes \sigma_z \otimes\sigma_z,&\quad \rho(A_{13})=\tfrac12 \sigma_z\otimes \sigma_x\otimes\sigma_z,&\quad \rho(A_{20})=\tfrac12 \epsilon\otimes \sigma_z \otimes I,\\ \rho(A_7)=\tfrac12 I\otimes \epsilon \otimes\sigma_x, &\quad \rho(A_{14})=\tfrac12 \sigma_z\otimes \epsilon\otimes I, &\quad \rho(A_{21})=\tfrac12 \sigma_x\otimes I \otimes I. \end{array} \end{align} $$
The spin representation
![]() $\rho $
of
$\rho $
of
![]() $V_0=\mathbb {R}\oplus \mathfrak {so}(4,3)$
needs one generator more. Let us call it
$V_0=\mathbb {R}\oplus \mathfrak {so}(4,3)$
needs one generator more. Let us call it
![]() $\rho (A_{22})$
. We have
$\rho (A_{22})$
. We have
We determine the structure constants
![]() $c^K{}_{IJ}$
of
$c^K{}_{IJ}$
of
![]() $\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the basis
$\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the basis
![]() $A_I$
from
$A_I$
from
8.1.2. Obtaining the vectorial representation of
 $\mathfrak {so}(4,3)$
$\mathfrak {so}(4,3)$
Now, we take the space
![]() $\bigwedge ^2S$
and consider the skew symmetric representation
$\bigwedge ^2S$
and consider the skew symmetric representation
in it. We will write it in the standard basis
![]() $f_\mu $
,
$f_\mu $
,
![]() $\mu =1,\dots , 8$
in
$\mu =1,\dots , 8$
in
![]() $S=\mathbb {R}^8$
. We have
$S=\mathbb {R}^8$
. We have
![]() $\rho (A_I)f_\mu =\rho _I{}^\nu {}_\mu f_\nu $
. Now, the components of the 28-dimensional representation
$\rho (A_I)f_\mu =\rho _I{}^\nu {}_\mu f_\nu $
. Now, the components of the 28-dimensional representation
![]() ${\stackrel {\scriptscriptstyle {a}}{\rho }}{}=\rho \wedge \rho _1$
are
${\stackrel {\scriptscriptstyle {a}}{\rho }}{}=\rho \wedge \rho _1$
are
and we have
The Casimir operator for this representation is
where
![]() $K^{IJ}$
is the inverse of the Killing form matrix
$K^{IJ}$
is the inverse of the Killing form matrix
![]() $K_{IJ}=c^L{}_{IM}c^M{}_{JL}$
in the basis
$K_{IJ}=c^L{}_{IM}c^M{}_{JL}$
in the basis
![]() $A_I$
. Since for the Killing form to be nondegenerate we must restrict to the semisimple part of
$A_I$
. Since for the Killing form to be nondegenerate we must restrict to the semisimple part of
![]() $\mathbb {R}\oplus \mathfrak {so}(4,3)$
, here the indices
$\mathbb {R}\oplus \mathfrak {so}(4,3)$
, here the indices
![]() $I,J,K,L,M=1,2\dots ,21$
, and as always are summed over the repeated indices. One can check that in this basis of
$I,J,K,L,M=1,2\dots ,21$
, and as always are summed over the repeated indices. One can check that in this basis of
![]() $\mathfrak {so}(4,3)$
, the Killing form matrix is diagonal and reads
$\mathfrak {so}(4,3)$
, the Killing form matrix is diagonal and reads
The Casimir
![]() $\mathcal C$
defines the decomposition of the 28-dimensional reducible representation
$\mathcal C$
defines the decomposition of the 28-dimensional reducible representation
![]() ${\stackrel {\scriptscriptstyle {a}}{\rho }}{}=\rho _1\wedge \rho _1$
onto
${\stackrel {\scriptscriptstyle {a}}{\rho }}{}=\rho _1\wedge \rho _1$
onto
where the 7-dimensional irreducible representation space
![]() $\bigwedge _7$
is the eigenspace of the Casimir operator consisting of eigen-bispinors with eigenvalue equal to 6,
$\bigwedge _7$
is the eigenspace of the Casimir operator consisting of eigen-bispinors with eigenvalue equal to 6,
Explicitly, in the same basis
![]() $A_I$
,
$A_I$
,
![]() $I=1,2,\dots ,21$
as before, this 7-dimensional representation
$I=1,2,\dots ,21$
as before, this 7-dimensional representation
![]() $(\tau ,R=\bigwedge _7)$
of the
$(\tau ,R=\bigwedge _7)$
of the
![]() $\mathfrak {so}(4,3)$
Lie algebra is given by
$\mathfrak {so}(4,3)$
Lie algebra is given by
 $$ \begin{align}\begin{aligned} &\tau(A_1)=E_{66}-E_{22},\\ &\tau(A_2)=\tfrac12(E_{23}-E_{32}+E_{25}-E_{52}+E_{36}-E_{63}+E_{56}-E_{65}),\\ &\tau(A_3)=\tfrac12(E_{23}+E_{32}+E_{25}+E_{52}+E_{36}+E_{63}+E_{56}+E_{65}),\\ &\tau(A_4)=\tfrac12(E_{23}+E_{32}-E_{25}-E_{52}-E_{36}-E_{63}+E_{56}+E_{65}),\\ &\tau(A_5)=\tfrac12(E_{23}-E_{32}-E_{25}+E_{52}-E_{36}+E_{63}+E_{56}-E_{65}),\\ &\tau(A_6)=E_{33}-E_{55},\\ &\tau(A_7)=\tfrac12(E_{12}-E_{21}-E_{16}+E_{61}-E_{27}+E_{72}+E_{67}-E_{76}),\\ &\tau(A_8)=\tfrac12(-E_{12}-E_{21}-E_{16}-E_{61}-E_{27}-E_{72}-E_{67}-E_{76}),\\ &\tau(A_9)=\tfrac12(E_{13}-E_{31}+E_{15}-E_{51}-E_{37}+E_{73}-E_{57}+E_{75}),\\ &\tau(A_{10})=\tfrac12(E_{13}+E_{31}-E_{15}-E_{51}+E_{37}+E_{73}-E_{57}-E_{75}),\\ &\tau(A_{11})=\tfrac12(-E_{12}-E_{21}+E_{16}+E_{61}+E_{27}+E_{72}-E_{67}-E_{76}),\\ &\tau(A_{12})=\tfrac12(E_{12}-E_{21}+E_{16}-E_{61}+E_{27}-E_{72}+E_{67}-E_{76}),\\ &\tau(A_{13})=\tfrac12(-E_{13}-E_{31}-E_{15}-E_{51}+E_{37}+E_{73}+E_{57}+E_{75}),\\ &\tau(A_{14})=\tfrac12(-E_{13}+E_{31}+E_{15}-E_{51}-E_{37}+E_{73}+E_{57}-E_{75}),\\ &\tau(A_{15})=E_{11}-E_{77},\\ &\tau(A_{16})=\tfrac12(2E_{24}-E_{42}+E_{46}-2E_{64}),\\ &\tau(A_{17})=\tfrac12(2E_{24}+E_{42}+E_{46}+2E_{64}),\\ &\tau(A_{18})=\tfrac12(2E_{34}-E_{43}-E_{45}+2E_{54}),\\ &\tau(A_{19})=\tfrac12(-2E_{34}-E_{43}+E_{45}+2E_{54}),\\ &\tau(A_{20})=\tfrac12(-2E_{14}+E_{41}+E_{47}-2E_{74}),\\ &\tau(A_{21})=\tfrac12(2E_{14}+E_{41}-E_{47}-2E_{74}),\\ &\tau(A_{22})=E_{11}+E_{22}+E_{33}+E_{44}+E_{55}+E_{66}+E_{77}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &\tau(A_1)=E_{66}-E_{22},\\ &\tau(A_2)=\tfrac12(E_{23}-E_{32}+E_{25}-E_{52}+E_{36}-E_{63}+E_{56}-E_{65}),\\ &\tau(A_3)=\tfrac12(E_{23}+E_{32}+E_{25}+E_{52}+E_{36}+E_{63}+E_{56}+E_{65}),\\ &\tau(A_4)=\tfrac12(E_{23}+E_{32}-E_{25}-E_{52}-E_{36}-E_{63}+E_{56}+E_{65}),\\ &\tau(A_5)=\tfrac12(E_{23}-E_{32}-E_{25}+E_{52}-E_{36}+E_{63}+E_{56}-E_{65}),\\ &\tau(A_6)=E_{33}-E_{55},\\ &\tau(A_7)=\tfrac12(E_{12}-E_{21}-E_{16}+E_{61}-E_{27}+E_{72}+E_{67}-E_{76}),\\ &\tau(A_8)=\tfrac12(-E_{12}-E_{21}-E_{16}-E_{61}-E_{27}-E_{72}-E_{67}-E_{76}),\\ &\tau(A_9)=\tfrac12(E_{13}-E_{31}+E_{15}-E_{51}-E_{37}+E_{73}-E_{57}+E_{75}),\\ &\tau(A_{10})=\tfrac12(E_{13}+E_{31}-E_{15}-E_{51}+E_{37}+E_{73}-E_{57}-E_{75}),\\ &\tau(A_{11})=\tfrac12(-E_{12}-E_{21}+E_{16}+E_{61}+E_{27}+E_{72}-E_{67}-E_{76}),\\ &\tau(A_{12})=\tfrac12(E_{12}-E_{21}+E_{16}-E_{61}+E_{27}-E_{72}+E_{67}-E_{76}),\\ &\tau(A_{13})=\tfrac12(-E_{13}-E_{31}-E_{15}-E_{51}+E_{37}+E_{73}+E_{57}+E_{75}),\\ &\tau(A_{14})=\tfrac12(-E_{13}+E_{31}+E_{15}-E_{51}-E_{37}+E_{73}+E_{57}-E_{75}),\\ &\tau(A_{15})=E_{11}-E_{77},\\ &\tau(A_{16})=\tfrac12(2E_{24}-E_{42}+E_{46}-2E_{64}),\\ &\tau(A_{17})=\tfrac12(2E_{24}+E_{42}+E_{46}+2E_{64}),\\ &\tau(A_{18})=\tfrac12(2E_{34}-E_{43}-E_{45}+2E_{54}),\\ &\tau(A_{19})=\tfrac12(-2E_{34}-E_{43}+E_{45}+2E_{54}),\\ &\tau(A_{20})=\tfrac12(-2E_{14}+E_{41}+E_{47}-2E_{74}),\\ &\tau(A_{21})=\tfrac12(2E_{14}+E_{41}-E_{47}-2E_{74}),\\ &\tau(A_{22})=E_{11}+E_{22}+E_{33}+E_{44}+E_{55}+E_{66}+E_{77}, \end{aligned}\end{align} $$
where
![]() $E_{ij}$
,
$E_{ij}$
,
![]() $i,j=1,2,\dots ,7$
denote
$i,j=1,2,\dots ,7$
denote
![]() $7\times 7$
matrices with zeroes everywhere except the value 1 in the entry
$7\times 7$
matrices with zeroes everywhere except the value 1 in the entry
![]() $(i,j)$
seating at the crossing of the ith row and the jth column.
$(i,j)$
seating at the crossing of the ith row and the jth column.
One can check that
with the same structure constants as in (8.3).
8.1.3. A contactification with
 $\mathfrak {f}_I$
symmetry
$\mathfrak {f}_I$
symmetry
So now we are in the situation of having two representations
![]() $(\rho ,S)$
and
$(\rho ,S)$
and
![]() $(\tau ,R=\bigwedge _7)$
od
$(\tau ,R=\bigwedge _7)$
od
![]() $\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
, and we can try to solve the equation (2.1) for the map
$\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
, and we can try to solve the equation (2.1) for the map
![]() $\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
. Of course, if we started with some arbitrary
$\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
. Of course, if we started with some arbitrary
![]() $\rho $
and
$\rho $
and
![]() $\tau $
, this equation would not have solutions other than 0, but here we expect to have solution since we know it from the Cartan’s PhD thesis [Reference Cartan8] and the announcement in Helgason’s paper [Reference Helgason13]. And indeed, there is a solution for a nonzero
$\tau $
, this equation would not have solutions other than 0, but here we expect to have solution since we know it from the Cartan’s PhD thesis [Reference Cartan8] and the announcement in Helgason’s paper [Reference Helgason13]. And indeed, there is a solution for a nonzero
![]() $\omega $
, which when written in the basis
$\omega $
, which when written in the basis
![]() $\{f_\mu \}$
in S and
$\{f_\mu \}$
in S and
![]() $\{e_i\}$
in R is such that it gives the seven 2-forms
$\{e_i\}$
in R is such that it gives the seven 2-forms
![]() $\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
,
$\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
,
![]() $i=1,\dots ,7$
, in
$i=1,\dots ,7$
, in
![]() $N=\mathbb {R}^8$
given by
$N=\mathbb {R}^8$
given by
 $$ \begin{align}\begin{aligned} \omega^1&=\mathrm{d} x^1\wedge\mathrm{d} x^2-\mathrm{d} x^7\wedge\mathrm{d} x^8,\\ \omega^2&=\mathrm{d} x^2\wedge\mathrm{d} x^4-\mathrm{d} x^6\wedge\mathrm{d} x^8,\\ \omega^3&=\mathrm{d} x^1\wedge\mathrm{d} x^4-\mathrm{d} x^5\wedge\mathrm{d} x^8,\\ \omega^4&=\tfrac12\,\big(\,\mathrm{d} x^1\wedge\mathrm{d} x^6-\mathrm{d} x^2\wedge\mathrm{d} x^5-\mathrm{d} x^3\wedge\mathrm{d} x^8+\mathrm{d} x^4\wedge\mathrm{d} x^7\,\big),\\ \omega^5&=\mathrm{d} x^2\wedge\mathrm{d} x^3-\mathrm{d} x^6\wedge\mathrm{d} x^7,\\ \omega^6&=\mathrm{d} x^1\wedge\mathrm{d} x^3-\mathrm{d} x^5\wedge\mathrm{d} x^7,\\ \omega^7&=\mathrm{d} x^3\wedge\mathrm{d} x^4-\mathrm{d} x^5\wedge\mathrm{d} x^6. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \omega^1&=\mathrm{d} x^1\wedge\mathrm{d} x^2-\mathrm{d} x^7\wedge\mathrm{d} x^8,\\ \omega^2&=\mathrm{d} x^2\wedge\mathrm{d} x^4-\mathrm{d} x^6\wedge\mathrm{d} x^8,\\ \omega^3&=\mathrm{d} x^1\wedge\mathrm{d} x^4-\mathrm{d} x^5\wedge\mathrm{d} x^8,\\ \omega^4&=\tfrac12\,\big(\,\mathrm{d} x^1\wedge\mathrm{d} x^6-\mathrm{d} x^2\wedge\mathrm{d} x^5-\mathrm{d} x^3\wedge\mathrm{d} x^8+\mathrm{d} x^4\wedge\mathrm{d} x^7\,\big),\\ \omega^5&=\mathrm{d} x^2\wedge\mathrm{d} x^3-\mathrm{d} x^6\wedge\mathrm{d} x^7,\\ \omega^6&=\mathrm{d} x^1\wedge\mathrm{d} x^3-\mathrm{d} x^5\wedge\mathrm{d} x^7,\\ \omega^7&=\mathrm{d} x^3\wedge\mathrm{d} x^4-\mathrm{d} x^5\wedge\mathrm{d} x^6. \end{aligned}\end{align} $$
These, via the contactification and the theory summarised in Corollary 4.1, lead to the following theorem.
Theorem 8.1. Let
![]() $M=\mathbb {R}^{15}$
with coordinates
$M=\mathbb {R}^{15}$
with coordinates
![]() $(u^1,\dots ,u^7,x^1,\dots ,x^8)$
, and consider seven 1-forms
$(u^1,\dots ,u^7,x^1,\dots ,x^8)$
, and consider seven 1-forms
![]() $\lambda ^i,\dots ,\lambda ^7$
on M given by
$\lambda ^i,\dots ,\lambda ^7$
on M given by
 $$ \begin{align*}\begin{aligned} \lambda^1&=\mathrm{d} u^1+ x^1\mathrm{d} x^2- x^7\mathrm{d} x^8,\\ \lambda^2&=\mathrm{d} u^2+ x^2\mathrm{d} x^4- x^6\mathrm{d} x^8,\\ \lambda^3&=\mathrm{d} u^3+ x^1\mathrm{d} x^4- x^5\mathrm{d} x^8,\\ \lambda^4&=\mathrm{d} u^4+\tfrac12\,\big(\, x^1\mathrm{d} x^6- x^2\mathrm{d} x^5-x^3\mathrm{d} x^8+ x^4\mathrm{d} x^7\,\big),\\ \lambda^5&=\mathrm{d} u^5+x^2\mathrm{d} x^3- x^6\mathrm{d} x^7,\\ \lambda^6&=\mathrm{d} u^6+x^1\mathrm{d} x^3- x^5\mathrm{d} x^7,\\ \lambda^7&=\mathrm{d} u^7+x^3\mathrm{d} x^4- x^5\mathrm{d} x^6. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1&=\mathrm{d} u^1+ x^1\mathrm{d} x^2- x^7\mathrm{d} x^8,\\ \lambda^2&=\mathrm{d} u^2+ x^2\mathrm{d} x^4- x^6\mathrm{d} x^8,\\ \lambda^3&=\mathrm{d} u^3+ x^1\mathrm{d} x^4- x^5\mathrm{d} x^8,\\ \lambda^4&=\mathrm{d} u^4+\tfrac12\,\big(\, x^1\mathrm{d} x^6- x^2\mathrm{d} x^5-x^3\mathrm{d} x^8+ x^4\mathrm{d} x^7\,\big),\\ \lambda^5&=\mathrm{d} u^5+x^2\mathrm{d} x^3- x^6\mathrm{d} x^7,\\ \lambda^6&=\mathrm{d} u^6+x^1\mathrm{d} x^3- x^5\mathrm{d} x^7,\\ \lambda^7&=\mathrm{d} u^7+x^3\mathrm{d} x^4- x^5\mathrm{d} x^6. \end{aligned}\end{align*} $$
The rank 8 distribution
![]() ${\mathcal D}$
on M defined as
${\mathcal D}$
on M defined as ![]() has its Lie algebra of infinitesimal authomorphism
has its Lie algebra of infinitesimal authomorphism
![]() $\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^8)$
is the spinorial representation (8.2) of
$(\rho ,S=\mathbb {R}^8)$
is the spinorial representation (8.2) of
![]() $\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}\big (4,3)$
and
$\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}\big (4,3)$
and
![]() $(\tau ,R=\mathbb {R}^7)$
is the vectorial representation (8.4) of
$(\tau ,R=\mathbb {R}^7)$
is the vectorial representation (8.4) of
![]() $\mathfrak {n}_{00}$
.
$\mathfrak {n}_{00}$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple Lie algebra
![]() $\mathfrak {f}_I$
,
$\mathfrak {f}_I$
,
having the following natural gradation:
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S$
,
$\mathfrak {n}_{-1}=S$
,
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
$\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {f}_I$
.
$\mathfrak {f}_I$
.
The contactification
![]() $(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
![]() $(F_I,P_I)$
related to the following crossed Satake diagram
$(F_I,P_I)$
related to the following crossed Satake diagram ![]() of
of
![]() $\mathfrak {f}_I$
.
$\mathfrak {f}_I$
.
Remark 8.2. Please note that this is an example of an application of the magical equation (2.1) in which the starting algebra
![]() $\mathfrak {n}_{00}$
was big enough, so that its Tanaka prolongation
$\mathfrak {n}_{00}$
was big enough, so that its Tanaka prolongation
![]() $\mathfrak {n}_0$
counterpart is precisely equal to
$\mathfrak {n}_0$
counterpart is precisely equal to
![]() $\mathfrak {n}_{00}$
. This was actually expected from the construction based on the crossed Satake diagram,
$\mathfrak {n}_{00}$
. This was actually expected from the construction based on the crossed Satake diagram, ![]() , which shows that
, which shows that
![]() $\mathfrak {n}_0$
of this parabolic geometry is precisely our
$\mathfrak {n}_0$
of this parabolic geometry is precisely our
![]() $\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
.
$\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}(4,3)$
.
Remark 8.3. One sees that the distribution
![]() $\mathcal D$
in
$\mathcal D$
in
![]() $\mathbb {R}^{15}$
with
$\mathbb {R}^{15}$
with
![]() $\mathfrak {f}_I$
symmetry presented in Theorem 8.1 looks different that the distribution from our Example 1.3. It follows, however, that both these distributions are locally equivalent, and both have the same simple exceptional Lie algebra
$\mathfrak {f}_I$
symmetry presented in Theorem 8.1 looks different that the distribution from our Example 1.3. It follows, however, that both these distributions are locally equivalent, and both have the same simple exceptional Lie algebra
![]() $\mathfrak {f}_I$
as an algebra of their authomorphisms.
$\mathfrak {f}_I$
as an algebra of their authomorphisms.
8.1.4. Contactification for
 $\mathfrak {f}_I$
: more algebra about
$\mathfrak {f}_I$
: more algebra about
 $\mathfrak {so}(4,3)$
$\mathfrak {so}(4,3)$
In our construction of the
![]() $\mathfrak {f}_I$
symmetric distribution
$\mathfrak {f}_I$
symmetric distribution
![]() $\mathcal D$
in Theorem 8.1, the crucial role was played by the 7-dimensional span of 2-forms
$\mathcal D$
in Theorem 8.1, the crucial role was played by the 7-dimensional span of 2-forms
![]() $\omega ^i$
,
$\omega ^i$
,
![]() $i=1,2,\dots ,7$
. If we were given these seven 2-forms, we would produce the
$i=1,2,\dots ,7$
. If we were given these seven 2-forms, we would produce the
![]() $\mathfrak {f}_I$
symmetric distribution
$\mathfrak {f}_I$
symmetric distribution
![]() $\mathcal D$
by the procedure of contactification.
$\mathcal D$
by the procedure of contactification.
It turns out that in
![]() $S=\mathbb {R}^8$
, there is a particular 4-formFootnote
3
$S=\mathbb {R}^8$
, there is a particular 4-formFootnote
3
that is
![]() $\mathbb {R}\oplus \mathfrak {so}(4,3)$
invariant
$\mathbb {R}\oplus \mathfrak {so}(4,3)$
invariant
It may be represented by
where
![]() $\omega ^i$
are given by (8.5) and
$\omega ^i$
are given by (8.5) and
 $$ \begin{align*}\big(\,\,h_{ij}\,\,\big)\,\,=\,\,\tfrac12\,\, \begin{pmatrix} 0&0&0&0&0&0&1\\0&0&0&0&0&-1&0\\0&0&0&0&1&0&0\\0&0&0&1&0&0&0\\0&0&1&0&0&0&0\\0&-1&0&0&0&0&0\\1&0&0&0&0&0&0 \end{pmatrix},\end{align*} $$
$$ \begin{align*}\big(\,\,h_{ij}\,\,\big)\,\,=\,\,\tfrac12\,\, \begin{pmatrix} 0&0&0&0&0&0&1\\0&0&0&0&0&-1&0\\0&0&0&0&1&0&0\\0&0&0&1&0&0&0\\0&0&1&0&0&0&0\\0&-1&0&0&0&0&0\\1&0&0&0&0&0&0 \end{pmatrix},\end{align*} $$
or in wordsFootnote
4
:
![]() $h_{ij}$
,
$h_{ij}$
,
![]() $i,j,=1,2,\dots ,7$
, are all zero except
$i,j,=1,2,\dots ,7$
, are all zero except
![]() $h_{17}=h_{71}=-h_{26}=-h_{62}=h_{35}=h_{53}=h_{44}=1$
.
$h_{17}=h_{71}=-h_{26}=-h_{62}=h_{35}=h_{53}=h_{44}=1$
.
The form
![]() $\Phi $
in full beauty reads
$\Phi $
in full beauty reads
 $$ \begin{align}\begin{aligned} \tfrac23\Phi\,\,=\,\,2\,\,\Big(\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^4+\mathrm{d} x^5\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7\wedge\mathrm{d} x^8\,\,\Big)-\\ &\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^6+\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^6\wedge\mathrm{d} x^8-\\&\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7-\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^5\wedge\mathrm{d} x^8+\\&\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^7-\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{ d} x^7\wedge\mathrm{d} x^8. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \tfrac23\Phi\,\,=\,\,2\,\,\Big(\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^4+\mathrm{d} x^5\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7\wedge\mathrm{d} x^8\,\,\Big)-\\ &\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^6+\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^6\wedge\mathrm{d} x^8-\\&\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7-\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^5\wedge\mathrm{d} x^8+\\&\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^7-\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{ d} x^7\wedge\mathrm{d} x^8. \end{aligned} \end{align} $$
Remark 8.4. It is remarkable that this 4-form alone encaptures all the features of the
![]() $\mathfrak {f}_I$
symmetric contactification we discussed in the entire Section 8.1. By this, we mean following:
$\mathfrak {f}_I$
symmetric contactification we discussed in the entire Section 8.1. By this, we mean following:
-
(1) Consider
 $N=\mathbb {R}^8$
with coordinates
$N=\mathbb {R}^8$
with coordinates
 $(x^\mu )$
,
$(x^\mu )$
,
 $\mu =1,2,\dots ,8$
and the 4-form given by (8.6).
$\mu =1,2,\dots ,8$
and the 4-form given by (8.6). $$ \begin{align*}\Phi=\tfrac{1}{4!}\Phi_{\mu\nu\rho\sigma}\mathrm{d} x^\mu\wedge\mathrm{d} x^\nu\wedge\mathrm{d} x^\rho\wedge \mathrm{ d} x^\sigma\end{align*} $$
$$ \begin{align*}\Phi=\tfrac{1}{4!}\Phi_{\mu\nu\rho\sigma}\mathrm{d} x^\mu\wedge\mathrm{d} x^\nu\wedge\mathrm{d} x^\rho\wedge \mathrm{ d} x^\sigma\end{align*} $$
-
(2) Consider an equation
for the real $$ \begin{align*}A^\alpha{}_\mu \Phi_{\alpha\nu\rho\sigma}+A^\alpha{}_\nu \Phi_{\mu\alpha\rho\sigma}+A^\alpha{}_\rho \Phi_{\mu\nu\alpha\sigma}+A^\alpha{}_\sigma \Phi_{\mu\nu\rho\alpha}=S\Phi_{\mu\nu\rho\sigma}\end{align*} $$
$$ \begin{align*}A^\alpha{}_\mu \Phi_{\alpha\nu\rho\sigma}+A^\alpha{}_\nu \Phi_{\mu\alpha\rho\sigma}+A^\alpha{}_\rho \Phi_{\mu\nu\alpha\sigma}+A^\alpha{}_\sigma \Phi_{\mu\nu\rho\alpha}=S\Phi_{\mu\nu\rho\sigma}\end{align*} $$
 $7\times 7$
matrix
$7\times 7$
matrix
 $A=(A^\mu {}_\nu )$
.
$A=(A^\mu {}_\nu )$
.
-
(3) For simplicity, solve it in two steps:
-
• First with
 $S=0$
. You obtain 21-dimensional solution space, which will be the spin representation
$S=0$
. You obtain 21-dimensional solution space, which will be the spin representation
 $\rho $
of
$\rho $
of
 $\mathfrak {so}(4,3)$
. It is given
$\mathfrak {so}(4,3)$
. It is given
 $\rho (A)=A$
.
$\rho (A)=A$
. -
• Then prove that the only solution with
 $S\neq 0$
corresponds to
$S\neq 0$
corresponds to
 $S=4$
, and that, modulo the addition of linear combinations of solutions with
$S=4$
, and that, modulo the addition of linear combinations of solutions with
 $S=0$
, it is given by
$S=0$
, it is given by
 $A=\mathrm {Id}_{8\times 8}$
. Extend your possible As with
$A=\mathrm {Id}_{8\times 8}$
. Extend your possible As with
 $S=0$
to As including
$S=0$
to As including
 $A=\mathrm {Id}_{8\times 8}$
.
$A=\mathrm {Id}_{8\times 8}$
.
-
-
(4) In this way, you will show that the stabiliser in
 $\mathfrak {gl}(8,\mathbb {R})$
of the 4-form
$\mathfrak {gl}(8,\mathbb {R})$
of the 4-form
 $\Phi $
is the Lie algebra
$\Phi $
is the Lie algebra
 $\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the spin representation
$\mathbb {R}\oplus \mathfrak {so}(4,3)$
in the spin representation
 $\rho $
of Pauli spinors;
$\rho $
of Pauli spinors;
 $\rho (A)=A$
.
$\rho (A)=A$
. -
(5) Then search for a 7-dimensional space of 2-forms spanned say by the 2-forms
 $\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
satisfying for all As from the spin representation
$\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
satisfying for all As from the spin representation $$ \begin{align*}A^\alpha{}_\mu\,\, \omega^i{}_{\alpha\nu}\,\,+\,\,A^\alpha{}_\nu\,\, \omega^i{}_{\mu\alpha}\,\,=\,\,s^i{}_j \,\,\omega^j{}_{\mu\nu}\,\,\end{align*} $$
$$ \begin{align*}A^\alpha{}_\mu\,\, \omega^i{}_{\alpha\nu}\,\,+\,\,A^\alpha{}_\nu\,\, \omega^i{}_{\mu\alpha}\,\,=\,\,s^i{}_j \,\,\omega^j{}_{\mu\nu}\,\,\end{align*} $$
 $\rho (A)=A$
of
$\rho (A)=A$
of
 $\mathbb {R}\oplus \mathfrak {so}(4,3)$
. Here,
$\mathbb {R}\oplus \mathfrak {so}(4,3)$
. Here,
 $s^i{}_j$
are auxiliary constantsFootnote
5
.
$s^i{}_j$
are auxiliary constantsFootnote
5
.
-
(6) This space is uniquely defined by these equations, and after solving them, you will get 7 linearly independent 2-forms
 $(\omega ^1,\dots ,\omega ^7)$
in
$(\omega ^1,\dots ,\omega ^7)$
in
 $N=\mathbb {R}^8$
.
$N=\mathbb {R}^8$
. -
(7) Contactifying the resulting structure
 $\big (N,\mathrm {Span}(\omega ^1,\dots ,\omega ^7)\big )$
, as we did, for example, in Theorem 8.1, you will get
$\big (N,\mathrm {Span}(\omega ^1,\dots ,\omega ^7)\big )$
, as we did, for example, in Theorem 8.1, you will get
 $\mathfrak {f}_I$
symmetric distribution
$\mathfrak {f}_I$
symmetric distribution
 ${\mathcal D}$
in
${\mathcal D}$
in
 $\mathbb {R}^7\to \big (\,M=\mathbb {R}^{15}\,\big )\to \big (\,N=\mathbb {R}^8\,\big )$
.
$\mathbb {R}^7\to \big (\,M=\mathbb {R}^{15}\,\big )\to \big (\,N=\mathbb {R}^8\,\big )$
.
8.2. Realisation of
 $\mathfrak {f}_{II}$
$\mathfrak {f}_{II}$
It seems that Cartan was only interested in the explicit realisation of
![]() $\mathfrak {f}_I$
. The realisation of
$\mathfrak {f}_I$
. The realisation of
![]() $\mathfrak {f}_{II}$
can be obtained in the same spirit as we have described in Section 8.1. Here, without much of the explanations since they parallel Section 8.1, we only display the main steps leading to this realisation.
$\mathfrak {f}_{II}$
can be obtained in the same spirit as we have described in Section 8.1. Here, without much of the explanations since they parallel Section 8.1, we only display the main steps leading to this realisation.
We start with the representation of the Clifford algebra
![]() ${\mathcal C}\ell (0,7)$
generated by the seven
${\mathcal C}\ell (0,7)$
generated by the seven
![]() $\rho $
-matrices from (5.4). They satisfy
$\rho $
-matrices from (5.4). They satisfy
They induce the 8-dimensional representation
of
![]() $n_{00}=\mathbb {R}\oplus \mathfrak {so}(0,7)$
in the space
$n_{00}=\mathbb {R}\oplus \mathfrak {so}(0,7)$
in the space
![]() $S=\mathbb {R}^8$
of real Pauli spinors, generated by the 22 real
$S=\mathbb {R}^8$
of real Pauli spinors, generated by the 22 real
![]() $8\times 8$
matrices:
$8\times 8$
matrices:
 $$ \begin{align*}\begin{aligned} &\rho(A_{I(i,j)})=\tfrac12\rho_i\rho_j, \quad 1\leq i<j\leq 7,\\ &\rho(A_{22})=\tfrac12 (I\otimes I\otimes I), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\rho(A_{I(i,j)})=\tfrac12\rho_i\rho_j, \quad 1\leq i<j\leq 7,\\ &\rho(A_{22})=\tfrac12 (I\otimes I\otimes I), \end{aligned} \end{align*} $$
with the index
![]() $I=I(i,j)$
given by (8.1) and with
$I=I(i,j)$
given by (8.1) and with
![]() $I,\sigma _x,\epsilon ,\sigma _z$
given by (5.1)–(5.2). Explicitly, in terms of matrices
$I,\sigma _x,\epsilon ,\sigma _z$
given by (5.1)–(5.2). Explicitly, in terms of matrices
![]() $I,\sigma _x,\epsilon ,\sigma _z$
, the generators of this spinorial representation of
$I,\sigma _x,\epsilon ,\sigma _z$
, the generators of this spinorial representation of
![]() $\mathfrak {so}(0,7)$
are
$\mathfrak {so}(0,7)$
are
 $$ \begin{align} \begin{array}{lll} \rho(A_1)=-\tfrac12 I\otimes \epsilon \otimes\sigma_z,&\quad \rho(A_8)=\tfrac12 \epsilon\otimes \sigma_z\otimes\sigma_z,&\quad \rho(A_{15})=-\tfrac12 I\otimes \epsilon \otimes I,\\ \rho(A_2)=\tfrac12 I\otimes \epsilon \otimes\sigma_x, &\quad\rho(A_9)=-\tfrac12 \epsilon\otimes \sigma_z \otimes\sigma_x, &\quad \rho(A_{16})=-\tfrac12 \sigma_x\otimes I \otimes\epsilon, \\ \rho(A_3)=-\tfrac12 I\otimes I \otimes\epsilon, &\quad\rho(A_{10})=-\tfrac12 I\otimes \sigma_z \otimes \epsilon,&\quad \rho(A_{17})=-\tfrac12 \sigma_x\otimes\epsilon \otimes\sigma_x,\\ \rho(A_4)=-\tfrac12 \epsilon\otimes \epsilon\otimes\epsilon,&\quad \rho(A_{11})=\tfrac12 \epsilon\otimes \sigma_z \otimes I,&\quad \rho(A_{18})=-\tfrac12 \sigma_x\otimes \epsilon \otimes\sigma_z,\\ \rho(A_5)=\tfrac12 \epsilon\otimes I \otimes\sigma_x,&\quad \rho(A_{12})=-\tfrac12 \epsilon\otimes \sigma_x \otimes\sigma_z,&\quad \rho(A_{19})=\tfrac12 \sigma_z\otimes \epsilon \otimes I,\\ \rho(A_6)=\tfrac12 \epsilon\otimes I\otimes\sigma_z,&\quad \rho(A_{13})=\tfrac12 \epsilon\otimes \sigma_x\otimes\sigma_x,&\quad \rho(A_{20})=\tfrac12 \sigma_z\otimes \sigma_x \otimes \epsilon,\\ \rho(A_7)=\tfrac12 \epsilon\otimes \sigma_x \otimes I, &\quad \rho(A_{14})=\tfrac12 I \otimes \sigma_x\otimes \epsilon, &\quad \rho(A_{21})=\tfrac12 \sigma_z\otimes \sigma_z \otimes \epsilon. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{lll} \rho(A_1)=-\tfrac12 I\otimes \epsilon \otimes\sigma_z,&\quad \rho(A_8)=\tfrac12 \epsilon\otimes \sigma_z\otimes\sigma_z,&\quad \rho(A_{15})=-\tfrac12 I\otimes \epsilon \otimes I,\\ \rho(A_2)=\tfrac12 I\otimes \epsilon \otimes\sigma_x, &\quad\rho(A_9)=-\tfrac12 \epsilon\otimes \sigma_z \otimes\sigma_x, &\quad \rho(A_{16})=-\tfrac12 \sigma_x\otimes I \otimes\epsilon, \\ \rho(A_3)=-\tfrac12 I\otimes I \otimes\epsilon, &\quad\rho(A_{10})=-\tfrac12 I\otimes \sigma_z \otimes \epsilon,&\quad \rho(A_{17})=-\tfrac12 \sigma_x\otimes\epsilon \otimes\sigma_x,\\ \rho(A_4)=-\tfrac12 \epsilon\otimes \epsilon\otimes\epsilon,&\quad \rho(A_{11})=\tfrac12 \epsilon\otimes \sigma_z \otimes I,&\quad \rho(A_{18})=-\tfrac12 \sigma_x\otimes \epsilon \otimes\sigma_z,\\ \rho(A_5)=\tfrac12 \epsilon\otimes I \otimes\sigma_x,&\quad \rho(A_{12})=-\tfrac12 \epsilon\otimes \sigma_x \otimes\sigma_z,&\quad \rho(A_{19})=\tfrac12 \sigma_z\otimes \epsilon \otimes I,\\ \rho(A_6)=\tfrac12 \epsilon\otimes I\otimes\sigma_z,&\quad \rho(A_{13})=\tfrac12 \epsilon\otimes \sigma_x\otimes\sigma_x,&\quad \rho(A_{20})=\tfrac12 \sigma_z\otimes \sigma_x \otimes \epsilon,\\ \rho(A_7)=\tfrac12 \epsilon\otimes \sigma_x \otimes I, &\quad \rho(A_{14})=\tfrac12 I \otimes \sigma_x\otimes \epsilon, &\quad \rho(A_{21})=\tfrac12 \sigma_z\otimes \sigma_z \otimes \epsilon. \end{array} \end{align} $$
We also write down the corresponding generators of the vectorial representation
![]() $\tau $
, which is the 7-dimensional irreducible component
$\tau $
, which is the 7-dimensional irreducible component
![]() $\bigwedge _7$
of the representation
$\bigwedge _7$
of the representation
![]() $\rho \wedge \rho $
, which decomposes as
$\rho \wedge \rho $
, which decomposes as
![]() $\bigwedge ^2S=\bigwedge _{21}\oplus \bigwedge _7$
. These generators read
$\bigwedge ^2S=\bigwedge _{21}\oplus \bigwedge _7$
. These generators read
 $$ \begin{align} \begin{array}{lll} \tau(A_1)=E_{31}-E_{13},&\quad \tau(A_8)=E_{37}-E_{73},&\quad \tau(A_{15})=E_{75}-E_{57},\\ \tau(A_2)=E_{12}-E_{21}, &\quad\tau(A_9)=E_{72}-E_{27}, &\quad \tau(A_{16})=E_{14}-E_{41}, \\ \tau(A_3)=E_{32}-E_{23}, &\quad\tau(A_{10})=E_{76}-E_{67},&\quad \tau(A_{17})=E_{34}-E_{43},\\ \tau(A_4)=E_{61}-E_{16},&\quad \tau(A_{11})=E_{51}-E_{15},&\quad \tau(A_{18})=E_{42}-E_{24},\\ \tau(A_5)=E_{36}-E_{63},&\quad \tau(A_{12})=E_{53}-E_{35},&\quad \tau(A_{19})=E_{46}-E_{64},\\ \tau(A_6)=E_{62}-E_{26},&\quad \tau(A_{13})=E_{25}-E_{52},&\quad \tau(A_{20})=E_{47}-E_{74},\\ \tau(A_7)=E_{17}-E_{71}, &\quad \tau(A_{14})= E_{65}-E_{56},&\quad \tau(A_{21})=E_{54}-E_{45}, \end{array} \end{align} $$
$$ \begin{align} \begin{array}{lll} \tau(A_1)=E_{31}-E_{13},&\quad \tau(A_8)=E_{37}-E_{73},&\quad \tau(A_{15})=E_{75}-E_{57},\\ \tau(A_2)=E_{12}-E_{21}, &\quad\tau(A_9)=E_{72}-E_{27}, &\quad \tau(A_{16})=E_{14}-E_{41}, \\ \tau(A_3)=E_{32}-E_{23}, &\quad\tau(A_{10})=E_{76}-E_{67},&\quad \tau(A_{17})=E_{34}-E_{43},\\ \tau(A_4)=E_{61}-E_{16},&\quad \tau(A_{11})=E_{51}-E_{15},&\quad \tau(A_{18})=E_{42}-E_{24},\\ \tau(A_5)=E_{36}-E_{63},&\quad \tau(A_{12})=E_{53}-E_{35},&\quad \tau(A_{19})=E_{46}-E_{64},\\ \tau(A_6)=E_{62}-E_{26},&\quad \tau(A_{13})=E_{25}-E_{52},&\quad \tau(A_{20})=E_{47}-E_{74},\\ \tau(A_7)=E_{17}-E_{71}, &\quad \tau(A_{14})= E_{65}-E_{56},&\quad \tau(A_{21})=E_{54}-E_{45}, \end{array} \end{align} $$
where
![]() $E_{ij}$
are
$E_{ij}$
are
![]() $7\times 7$
matrices with all zero entries, except at the ith-jth entry, where 1 resides.
$7\times 7$
matrices with all zero entries, except at the ith-jth entry, where 1 resides.
We are again in a position ready for application of our Lemma 2.1. Given the representations
![]() $(\rho ,S=\mathbb {R}^8)$
and
$(\rho ,S=\mathbb {R}^8)$
and
![]() $(\tau ,R=\bigwedge _7)$
of
$(\tau ,R=\bigwedge _7)$
of
![]() $\mathfrak {so}(0,7)$
, we solve the magical equation (2.1) for
$\mathfrak {so}(0,7)$
, we solve the magical equation (2.1) for
![]() $\omega =\tfrac 12\omega ^i{}_{\mu \nu }e_i\otimes f^\mu \wedge f^\nu $
. In this way, we obtain the seven 2-forms
$\omega =\tfrac 12\omega ^i{}_{\mu \nu }e_i\otimes f^\mu \wedge f^\nu $
. In this way, we obtain the seven 2-forms
![]() $\omega ^i=-\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
on
$\omega ^i=-\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
on
![]() $N=\mathbb {R}^8$
, with coordinates
$N=\mathbb {R}^8$
, with coordinates
![]() $(x^\mu )_{\mu =1}^8$
, which read as follows:
$(x^\mu )_{\mu =1}^8$
, which read as follows:
 $$ \begin{align}\begin{aligned} \omega^1&=-\mathrm{d} x^1\wedge\mathrm{d} x^2-\mathrm{d} x^3\wedge\mathrm{d} x^4+\mathrm{d} x^5\wedge\mathrm{d} x^6+\mathrm{d} x^7\wedge\mathrm{d} x^8,\\ \omega^2&=\mathrm{d} x^1\wedge\mathrm{d} x^3-\mathrm{d} x^2\wedge\mathrm{d} x^4-\mathrm{d} x^5\wedge\mathrm{d} x^7+\mathrm{d} x^6\wedge\mathrm{d} x^8,\\ \omega^3&=-\mathrm{d} x^1\wedge\mathrm{d} x^4-\mathrm{d} x^2\wedge\mathrm{d} x^3+\mathrm{d} x^5\wedge\mathrm{d} x^8+\mathrm{d} x^6\wedge\mathrm{d} x^7,\\ \omega^4&=\mathrm{d} x^1\wedge\mathrm{d} x^5+\mathrm{d} x^2\wedge\mathrm{d} x^6+\mathrm{d} x^3\wedge\mathrm{d} x^7+\mathrm{d} x^4\wedge\mathrm{d} x^8,\\ \omega^5&=-\mathrm{d} x^1\wedge\mathrm{d} x^6+\mathrm{d} x^2\wedge\mathrm{d} x^5+\mathrm{d} x^3\wedge\mathrm{d} x^8-\mathrm{d} x^4\wedge\mathrm{d} x^7,\\ \omega^6&=\mathrm{d} x^1\wedge\mathrm{d} x^7+\mathrm{d} x^2\wedge\mathrm{d} x^8-\mathrm{d} x^3\wedge\mathrm{d} x^5-\mathrm{d} x^4\wedge\mathrm{d} x^6,\\ \omega^7&=\mathrm{d} x^1\wedge\mathrm{d} x^8-\mathrm{d} x^2\wedge\mathrm{d} x^7+\mathrm{d} x^3\wedge\mathrm{d} x^6-\mathrm{d} x^4\wedge\mathrm{d} x^5. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \omega^1&=-\mathrm{d} x^1\wedge\mathrm{d} x^2-\mathrm{d} x^3\wedge\mathrm{d} x^4+\mathrm{d} x^5\wedge\mathrm{d} x^6+\mathrm{d} x^7\wedge\mathrm{d} x^8,\\ \omega^2&=\mathrm{d} x^1\wedge\mathrm{d} x^3-\mathrm{d} x^2\wedge\mathrm{d} x^4-\mathrm{d} x^5\wedge\mathrm{d} x^7+\mathrm{d} x^6\wedge\mathrm{d} x^8,\\ \omega^3&=-\mathrm{d} x^1\wedge\mathrm{d} x^4-\mathrm{d} x^2\wedge\mathrm{d} x^3+\mathrm{d} x^5\wedge\mathrm{d} x^8+\mathrm{d} x^6\wedge\mathrm{d} x^7,\\ \omega^4&=\mathrm{d} x^1\wedge\mathrm{d} x^5+\mathrm{d} x^2\wedge\mathrm{d} x^6+\mathrm{d} x^3\wedge\mathrm{d} x^7+\mathrm{d} x^4\wedge\mathrm{d} x^8,\\ \omega^5&=-\mathrm{d} x^1\wedge\mathrm{d} x^6+\mathrm{d} x^2\wedge\mathrm{d} x^5+\mathrm{d} x^3\wedge\mathrm{d} x^8-\mathrm{d} x^4\wedge\mathrm{d} x^7,\\ \omega^6&=\mathrm{d} x^1\wedge\mathrm{d} x^7+\mathrm{d} x^2\wedge\mathrm{d} x^8-\mathrm{d} x^3\wedge\mathrm{d} x^5-\mathrm{d} x^4\wedge\mathrm{d} x^6,\\ \omega^7&=\mathrm{d} x^1\wedge\mathrm{d} x^8-\mathrm{d} x^2\wedge\mathrm{d} x^7+\mathrm{d} x^3\wedge\mathrm{d} x^6-\mathrm{d} x^4\wedge\mathrm{d} x^5. \end{aligned}\end{align} $$
These, via the contactification, lead to the following theorem.
Theorem 8.5. Let
![]() $M=\mathbb {R}^{15}$
with coordinates
$M=\mathbb {R}^{15}$
with coordinates
![]() $(u^1,\dots ,u^7,x^1,\dots ,x^8)$
, and consider seven 1-forms
$(u^1,\dots ,u^7,x^1,\dots ,x^8)$
, and consider seven 1-forms
![]() $\lambda ^i,\dots ,\lambda ^7$
on M given by
$\lambda ^i,\dots ,\lambda ^7$
on M given by
 $$ \begin{align*}\begin{aligned} \lambda^1&=\mathrm{d} u^1- x^1\mathrm{d} x^2- x^3\mathrm{d} x^4+ x^5\mathrm{d} x^6+ x^7\mathrm{d} x^8,\\ \lambda^2&=\mathrm{d} u^2+ x^1\mathrm{d} x^3- x^2\mathrm{d} x^4-x^5\mathrm{d} x^7+x^6\mathrm{d} x^8,\\ \lambda^3&=\mathrm{d} u^3- x^1\mathrm{d} x^4- x^2\mathrm{d} x^3+ x^5\mathrm{d} x^8+ x^6\mathrm{d} x^7,\\ \lambda^4&=\mathrm{d} u^4+ x^1\mathrm{d} x^5+ x^2\mathrm{d} x^6+ x^3\mathrm{d} x^7+ x^4\mathrm{d} x^8,\\ \lambda^5&=\mathrm{d} u^5- x^1\mathrm{d} x^6+x^2\mathrm{d} x^5+x^3\mathrm{d} x^8-x^4\mathrm{d} x^7,\\ \lambda^6&=\mathrm{d} u^6+ x^1\mathrm{d} x^7+ x^2\mathrm{d} x^8- x^3\mathrm{d} x^5-x^4\mathrm{d} x^6,\\ \lambda^7&=\mathrm{d} u^7+ x^1\mathrm{d} x^8- x^2\mathrm{d} x^7+ x^3\mathrm{d} x^6 - x^4\mathrm{d} x^5. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1&=\mathrm{d} u^1- x^1\mathrm{d} x^2- x^3\mathrm{d} x^4+ x^5\mathrm{d} x^6+ x^7\mathrm{d} x^8,\\ \lambda^2&=\mathrm{d} u^2+ x^1\mathrm{d} x^3- x^2\mathrm{d} x^4-x^5\mathrm{d} x^7+x^6\mathrm{d} x^8,\\ \lambda^3&=\mathrm{d} u^3- x^1\mathrm{d} x^4- x^2\mathrm{d} x^3+ x^5\mathrm{d} x^8+ x^6\mathrm{d} x^7,\\ \lambda^4&=\mathrm{d} u^4+ x^1\mathrm{d} x^5+ x^2\mathrm{d} x^6+ x^3\mathrm{d} x^7+ x^4\mathrm{d} x^8,\\ \lambda^5&=\mathrm{d} u^5- x^1\mathrm{d} x^6+x^2\mathrm{d} x^5+x^3\mathrm{d} x^8-x^4\mathrm{d} x^7,\\ \lambda^6&=\mathrm{d} u^6+ x^1\mathrm{d} x^7+ x^2\mathrm{d} x^8- x^3\mathrm{d} x^5-x^4\mathrm{d} x^6,\\ \lambda^7&=\mathrm{d} u^7+ x^1\mathrm{d} x^8- x^2\mathrm{d} x^7+ x^3\mathrm{d} x^6 - x^4\mathrm{d} x^5. \end{aligned}\end{align*} $$
The rank 8 distribution
![]() ${\mathcal D}$
on M defined as
${\mathcal D}$
on M defined as ![]() has its Lie algebra of infinitesimal authomorphisms
has its Lie algebra of infinitesimal authomorphisms
![]() $\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^8)$
is the spinorial representation (8.7) of
$(\rho ,S=\mathbb {R}^8)$
is the spinorial representation (8.7) of
![]() $\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}\big (0,7)$
, and
$\mathfrak {n}_{00}=\mathbb {R}\oplus \mathfrak {so}\big (0,7)$
, and
![]() $(\tau ,R=\mathbb {R}^7)$
is the vectorial representation (8.8) of
$(\tau ,R=\mathbb {R}^7)$
is the vectorial representation (8.8) of
![]() $\mathfrak {n}_{00}$
.
$\mathfrak {n}_{00}$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple Lie algebra
![]() $\mathfrak {f}_{II}$
,
$\mathfrak {f}_{II}$
,
having the following natural gradation
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S$
,
$\mathfrak {n}_{-1}=S$
,
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
$\mathfrak {n}_{2}=R^*$
, which is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {f}_{II}$
.
$\mathfrak {f}_{II}$
.
The contactification
![]() $(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally a flat model for the parabolic geometry of type
![]() $(F_{II},P_{II})$
related to the following crossed Satake diagram
$(F_{II},P_{II})$
related to the following crossed Satake diagram ![]() of
of
![]() $\mathfrak {f}_{II}$
.
$\mathfrak {f}_{II}$
.
Remark 8.6. In this way, we realised the real form
![]() $\mathfrak {f}_{II}$
of the simple exceptional complex Lie algebra
$\mathfrak {f}_{II}$
of the simple exceptional complex Lie algebra
![]() $\mathfrak {f}_4$
in
$\mathfrak {f}_4$
in
![]() $M=\mathbb {R}^{15}$
as a symmetry algebra of the Pfaffian system
$M=\mathbb {R}^{15}$
as a symmetry algebra of the Pfaffian system
![]() $(\lambda ^1,\dots ,\lambda ^7)$
. This realisation does not appear in Cartan’s theses.
$(\lambda ^1,\dots ,\lambda ^7)$
. This realisation does not appear in Cartan’s theses.
Remark 8.7. Our present case of
![]() $\mathfrak {f}_{II}$
also admits description in terms of a certain
$\mathfrak {f}_{II}$
also admits description in terms of a certain
![]() $\mathbb {R}\oplus \mathfrak {so}(0,7)$
invariant 4-form
$\mathbb {R}\oplus \mathfrak {so}(0,7)$
invariant 4-form
![]() $\Phi $
in
$\Phi $
in
![]() $S=\mathbb {R}^8$
, analogous to the 4-form
$S=\mathbb {R}^8$
, analogous to the 4-form
![]() $\Phi $
introduced in Section 8.1.4, when we discussed
$\Phi $
introduced in Section 8.1.4, when we discussed
![]() $\mathfrak {f}_I$
. Skipping the details, we only mention that now
$\mathfrak {f}_I$
. Skipping the details, we only mention that now
![]() $\Phi $
may be represented by
$\Phi $
may be represented by
where
![]() $\omega ^i$
are given by (8.9) and
$\omega ^i$
are given by (8.9) and
 $$ \begin{align*}\big(\,\,h_{ij}\,\,\big)= \begin{pmatrix} -1&0&0&0&0&0&0\\0&-1&0&0&0&0&0\\0&0&-1&0&0&0&0\\0&0&0&-1&0&0&0\\0&0&0&0&-1&0&0\\0&0&0&0&0&-1&0\\0&0&0&0&0&0&-1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\big(\,\,h_{ij}\,\,\big)= \begin{pmatrix} -1&0&0&0&0&0&0\\0&-1&0&0&0&0&0\\0&0&-1&0&0&0&0\\0&0&0&-1&0&0&0\\0&0&0&0&-1&0&0\\0&0&0&0&0&-1&0\\0&0&0&0&0&0&-1 \end{pmatrix}.\end{align*} $$
Explicitly, the form
![]() $\Phi $
reads
$\Phi $
reads
 $$ \begin{align}\begin{aligned} -\tfrac16\Phi\,\,=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^4-\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^6-\\ &\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^7\wedge\mathrm{d} x^8-\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^5\wedge\mathrm{d} x^7+\\&\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^6\wedge\mathrm{d} x^8-\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^8-\\&\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7-\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{ d} x^5\wedge\mathrm{d} x^8-\\ &\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7+\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^7-\\&\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^8-\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^6-\\&\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^8+\mathrm{d} x^5\wedge\mathrm{d} x^6\wedge\mathrm{ d} x^7\wedge\mathrm{d} x^8. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} -\tfrac16\Phi\,\,=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^4-\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^6-\\ &\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^7\wedge\mathrm{d} x^8-\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^5\wedge\mathrm{d} x^7+\\&\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^6\wedge\mathrm{d} x^8-\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^8-\\&\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7-\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{ d} x^5\wedge\mathrm{d} x^8-\\ &\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^6\wedge\mathrm{d} x^7+\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^7-\\&\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^8-\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^6-\\&\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^8+\mathrm{d} x^5\wedge\mathrm{d} x^6\wedge\mathrm{ d} x^7\wedge\mathrm{d} x^8. \end{aligned} \end{align} $$
This 4-form alone encaptures all the features of the
![]() $\mathfrak {f}_{II}$
symmetric contactification we discussed in the entire Section 8.2. In particular, analogous statements as in Remark 8.4, with now
$\mathfrak {f}_{II}$
symmetric contactification we discussed in the entire Section 8.2. In particular, analogous statements as in Remark 8.4, with now
![]() $\mathfrak {so}(4,3)$
replaced by
$\mathfrak {so}(4,3)$
replaced by
![]() $\mathfrak {so}(0,7)$
, apply to the present 4-form
$\mathfrak {so}(0,7)$
, apply to the present 4-form
![]() $\Phi $
.
$\Phi $
.
9. Spinorial representations in dimension 8
Dimension eight is quite exceptional, as, for example, 8 is the highest possible dimension for the existence of Euclidean Hurwitz algebras, gifting us with the algebra of octonions. From the perspective of our paper, which meanders through the realm of simple Lie algebras, eight is very special: among all the complex simple Lie algebras, the Dynkin diagram of
![]() $\mathfrak {d}_4=\mathfrak {so}(8,\mathbb {C})$
which is defined in dimension eight, is the most symmetric:
$\mathfrak {d}_4=\mathfrak {so}(8,\mathbb {C})$
which is defined in dimension eight, is the most symmetric:

Visibly it has a threefold symmetry
![]() $S_3$
.
$S_3$
.
The Lie algebra
![]() $\mathfrak {so}(8,\mathbb {C})$
has six real forms. These are:
$\mathfrak {so}(8,\mathbb {C})$
has six real forms. These are:
![]() $\mathfrak {so}(8,0)$
,
$\mathfrak {so}(8,0)$
,
![]() $\mathfrak {so}(7,1)$
,
$\mathfrak {so}(7,1)$
,
![]() $\mathfrak {so}(6,2)$
,
$\mathfrak {so}(6,2)$
,
![]() $\mathfrak {so}^*(8)$
,
$\mathfrak {so}^*(8)$
,
![]() $\mathfrak {so}(5,3)$
and
$\mathfrak {so}(5,3)$
and
![]() $\mathfrak {so}(4,4)$
, with the following respective Satake diagrams:
$\mathfrak {so}(4,4)$
, with the following respective Satake diagrams:

We see that among these Satake diagrams, the only ones that share the
![]() $S_3$
symmetry of the Dynkin diagram of the complex algebra
$S_3$
symmetry of the Dynkin diagram of the complex algebra
![]() $\mathfrak {d}_4$
are those of the compact real form
$\mathfrak {d}_4$
are those of the compact real form
![]() $\mathfrak {so}(8,0)$
and of the split real form
$\mathfrak {so}(8,0)$
and of the split real form
![]() $\mathfrak {so}(4,4)$
.
$\mathfrak {so}(4,4)$
.
This
![]() $S_3$
symmetry of these two diagrams indicates that the lowest dimensional real representations of
$S_3$
symmetry of these two diagrams indicates that the lowest dimensional real representations of
![]() $\mathfrak {so}(4,4)$
and
$\mathfrak {so}(4,4)$
and
![]() $\mathfrak {so}(8,0)$
may have additional features when compared with spinorial representations of other
$\mathfrak {so}(8,0)$
may have additional features when compared with spinorial representations of other
![]() $\mathfrak {so}(p,q)$
s. In particular, for both
$\mathfrak {so}(p,q)$
s. In particular, for both
![]() $\mathfrak {so}(4,4)$
and
$\mathfrak {so}(4,4)$
and
![]() $\mathfrak {so}(8,0)$
, we have the following:
$\mathfrak {so}(8,0)$
, we have the following:
-
• Their Dirac representation
 $(\rho ,S)$
in the real vector space
$(\rho ,S)$
in the real vector space
 $S=\mathbb {R}^{16}$
is reducible over
$S=\mathbb {R}^{16}$
is reducible over
 $\mathbb {R}$
and is split into two real Weyl representations
$\mathbb {R}$
and is split into two real Weyl representations
 $(\rho _+,S_+)$
and
$(\rho _+,S_+)$
and
 $(\rho _-,S_-)$
in the respective vector spaces of Weyl spinors
$(\rho _-,S_-)$
in the respective vector spaces of Weyl spinors
 $S_+=\mathbb {R}^8$
and
$S_+=\mathbb {R}^8$
and
 $S_-=\mathbb {R}^8$
, which have the same real dimension eight,
$S_-=\mathbb {R}^8$
, which have the same real dimension eight,  $$ \begin{align*}\rho=\rho_+\oplus\rho_-\quad\mathrm{in}\quad S=S_+\oplus S_-, \quad \mathrm{dim}_{\mathbb{R}} S_\pm=8.\end{align*} $$
$$ \begin{align*}\rho=\rho_+\oplus\rho_-\quad\mathrm{in}\quad S=S_+\oplus S_-, \quad \mathrm{dim}_{\mathbb{R}} S_\pm=8.\end{align*} $$
-
• The real Weyl representations
 $(\rho _\pm ,S_\pm )$
are faithful, irreducible and nonequivalent.
$(\rho _\pm ,S_\pm )$
are faithful, irreducible and nonequivalent. -
• The defining representations
 $(\tau ,R)$
of
$(\tau ,R)$
of
 $\mathfrak {so}(4,4)$
and
$\mathfrak {so}(4,4)$
and
 $\mathfrak {so}(8,0)$
, as the algebra of endomorphisms in the space
$\mathfrak {so}(8,0)$
, as the algebra of endomorphisms in the space
 $R=\mathbb {R}^8$
of vectors preserving the bilinear form of respective signatures
$R=\mathbb {R}^8$
of vectors preserving the bilinear form of respective signatures
 $(4,4)$
and
$(4,4)$
and
 $(8,0)$
has the same dimension eight as the two Weyl representations
$(8,0)$
has the same dimension eight as the two Weyl representations
 $(\rho _\pm ,S_\pm )$
.
$(\rho _\pm ,S_\pm )$
. -
• The real defining representations
 $(\tau ,R)$
are irreducible for both
$(\tau ,R)$
are irreducible for both
 $\mathfrak {so}(4,4)$
and
$\mathfrak {so}(4,4)$
and
 $\mathfrak {so}(8,0)$
.
$\mathfrak {so}(8,0)$
. -
• All three real 8-dimensional irreducible representations
 $(\rho _+,S_+)$
,
$(\rho _+,S_+)$
,
 $(\rho _-,S_-)$
and
$(\rho _-,S_-)$
and
 $(\tau ,R)$
of, respectively, both
$(\tau ,R)$
of, respectively, both
 $\mathfrak {so}(4,4)$
and
$\mathfrak {so}(4,4)$
and
 $\mathfrak {so}(8,0)$
are pairwise nonequivalent.
$\mathfrak {so}(8,0)$
are pairwise nonequivalent.
Thus, the Lie algebras
![]() $\mathfrak {so}(4,4)$
and
$\mathfrak {so}(4,4)$
and
![]() $\mathfrak {so}(8,0)$
have three real, irreducible and nonequivalent representations
$\mathfrak {so}(8,0)$
have three real, irreducible and nonequivalent representations
![]() $(\rho _+,\rho _-,\tau )$
in the vector space
$(\rho _+,\rho _-,\tau )$
in the vector space
![]() $\mathbb {R}^8$
of the defining dimension
$\mathbb {R}^8$
of the defining dimension
![]() $p+q=8$
. For all
$p+q=8$
. For all
![]() $\mathfrak {so}(p,q)$
Lie algebras, this is the only dimension
$\mathfrak {so}(p,q)$
Lie algebras, this is the only dimension
![]() $p+q$
that such situation with the irreducible representations occurs.
$p+q$
that such situation with the irreducible representations occurs.
Below, we provide the explicit description of the triality representations
![]() $(\rho _+,\rho _-,\tau )$
separately for
$(\rho _+,\rho _-,\tau )$
separately for
![]() $\mathfrak {so}(4,4)$
and
$\mathfrak {so}(4,4)$
and
![]() $\mathfrak {so}(8,0)$
.
$\mathfrak {so}(8,0)$
.
9.1. Triality representations of
 $\mathfrak {so}(4,4)$
$\mathfrak {so}(4,4)$
We recall from Section 5 that the Lie algebra
![]() $\mathfrak {so}(4,4)$
admits a representation
$\mathfrak {so}(4,4)$
admits a representation
![]() $\rho $
in the 16-dimensional real vector space
$\rho $
in the 16-dimensional real vector space
![]() $S=\mathbb {R}^{16}$
of Dirac spinors. This is obtained by using the Dirac
$S=\mathbb {R}^{16}$
of Dirac spinors. This is obtained by using the Dirac
![]() $\gamma $
matrices generating the representation of the Clifford algebra
$\gamma $
matrices generating the representation of the Clifford algebra
![]() ${\mathcal C}\ell (4,4)$
. In terms of the 2-dimensional Pauli matrices
${\mathcal C}\ell (4,4)$
. In terms of the 2-dimensional Pauli matrices
![]() $(\sigma _x,\epsilon ,\sigma _z,I)$
, these look as follows:
$(\sigma _x,\epsilon ,\sigma _z,I)$
, these look as follows:
 $$ \begin{align} \begin{aligned} &\gamma_1=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_x\\ &\gamma_2=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\epsilon\\ &\gamma_3=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_z\\ &\gamma_4=\sigma_x\otimes\sigma_x\otimes\epsilon\otimes I\\ &\gamma_5=\sigma_x\otimes\sigma_x\otimes\sigma_z\otimes I\\ &\gamma_6=\sigma_x\otimes\epsilon\otimes I\otimes I\\ &\gamma_7=\sigma_x\otimes\sigma_z\otimes I\otimes I\\ &\gamma_8=\epsilon\otimes I\otimes I\otimes I. \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} &\gamma_1=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_x\\ &\gamma_2=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\epsilon\\ &\gamma_3=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_z\\ &\gamma_4=\sigma_x\otimes\sigma_x\otimes\epsilon\otimes I\\ &\gamma_5=\sigma_x\otimes\sigma_x\otimes\sigma_z\otimes I\\ &\gamma_6=\sigma_x\otimes\epsilon\otimes I\otimes I\\ &\gamma_7=\sigma_x\otimes\sigma_z\otimes I\otimes I\\ &\gamma_8=\epsilon\otimes I\otimes I\otimes I. \end{aligned}\end{align} $$
They satisfy the Dirac identity
with
The 28 generators of
![]() $\mathfrak {so}(4,4)$
in the Majorana-Dirac spinor representation
$\mathfrak {so}(4,4)$
in the Majorana-Dirac spinor representation
![]() $\rho $
in the space of Dirac spinors
$\rho $
in the space of Dirac spinors
![]() $S=\mathbb {R}^{16}$
are given by
$S=\mathbb {R}^{16}$
are given by
where we again have used the function
![]() $I=I(i,j)$
defined in (8.1). Note that since now
$I=I(i,j)$
defined in (8.1). Note that since now
![]() $i<j$
can run from 1 to 8, the function has a range from 1 to 28. We add to these generators the scaling generator,
$i<j$
can run from 1 to 8, the function has a range from 1 to 28. We add to these generators the scaling generator,
![]() $\rho (A_{29})$
,
$\rho (A_{29})$
,
This extends the Dirac representation
![]() $\rho $
of the Lie algebra
$\rho $
of the Lie algebra
![]() $\mathfrak {so}(4,4)$
to the representation of the homothety Lie algebra
$\mathfrak {so}(4,4)$
to the representation of the homothety Lie algebra
![]() $\mathfrak {co}(4,4)=\mathbb {R}\oplus \mathfrak {so}(4,4)$
.
$\mathfrak {co}(4,4)=\mathbb {R}\oplus \mathfrak {so}(4,4)$
.
In terms of the 2-dimensional Pauli matrices, these generators look like
 $$ \begin{align} \begin{array}{ll} \rho(A_1)= \tfrac12 I \otimes I\otimes I\otimes \sigma_z,&\rho(A_{15})=\tfrac12 I \otimes \sigma_z\otimes \sigma_z\otimes I,\\ \rho(A_2)= \tfrac12 I \otimes I\otimes I\otimes \epsilon ,&\rho(A_{16})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_x,\\ \rho(A_3)= \tfrac12 I \otimes I\otimes I\otimes \sigma_x ,&\rho(A_{17})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_4)=\tfrac12 I \otimes I\otimes \sigma_z\otimes \sigma_x,&\rho(A_{18})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho(A_5)= \tfrac12 I \otimes I\otimes \sigma_z\otimes \epsilon,&\rho(A_{19})=\tfrac12 I \otimes \epsilon\otimes \epsilon\otimes I ,\\ \rho(A_6)= \tfrac12 I \otimes I\otimes \sigma_z\otimes \sigma_z,&\rho(A_{20})=\tfrac12 I \otimes \epsilon\otimes \sigma_z\otimes I ,\\ \rho(A_7)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_x,&\rho(A_{21})=\tfrac12 I \otimes \sigma_x\otimes I\otimes I,\\ \rho(A_8)= \tfrac12 I \otimes I\otimes \epsilon\otimes \epsilon,&\rho(A_{22})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \sigma_x ,\\ \rho(A_9)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_z,&\rho(A_{23})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_{10})=\tfrac12 I \otimes I\otimes \sigma_x\otimes I,&\rho(A_{24})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \sigma_z ,\\ \rho(A_{11})= \tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \sigma_x ,&\rho(A_{25})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes I ,\\ \rho(A_{12})= \tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho(A_{26})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_z\otimes I ,\\ \rho(A_{13})= \tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \sigma_z,&\rho(A_{27})=\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes I,\\ \rho(A_{14})= \tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes I,&\rho(A_{28})=\tfrac12 \sigma_z \otimes \sigma_z\otimes I\otimes I. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \rho(A_1)= \tfrac12 I \otimes I\otimes I\otimes \sigma_z,&\rho(A_{15})=\tfrac12 I \otimes \sigma_z\otimes \sigma_z\otimes I,\\ \rho(A_2)= \tfrac12 I \otimes I\otimes I\otimes \epsilon ,&\rho(A_{16})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_x,\\ \rho(A_3)= \tfrac12 I \otimes I\otimes I\otimes \sigma_x ,&\rho(A_{17})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_4)=\tfrac12 I \otimes I\otimes \sigma_z\otimes \sigma_x,&\rho(A_{18})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho(A_5)= \tfrac12 I \otimes I\otimes \sigma_z\otimes \epsilon,&\rho(A_{19})=\tfrac12 I \otimes \epsilon\otimes \epsilon\otimes I ,\\ \rho(A_6)= \tfrac12 I \otimes I\otimes \sigma_z\otimes \sigma_z,&\rho(A_{20})=\tfrac12 I \otimes \epsilon\otimes \sigma_z\otimes I ,\\ \rho(A_7)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_x,&\rho(A_{21})=\tfrac12 I \otimes \sigma_x\otimes I\otimes I,\\ \rho(A_8)= \tfrac12 I \otimes I\otimes \epsilon\otimes \epsilon,&\rho(A_{22})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \sigma_x ,\\ \rho(A_9)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_z,&\rho(A_{23})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_{10})=\tfrac12 I \otimes I\otimes \sigma_x\otimes I,&\rho(A_{24})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \sigma_z ,\\ \rho(A_{11})= \tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \sigma_x ,&\rho(A_{25})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes I ,\\ \rho(A_{12})= \tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho(A_{26})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_z\otimes I ,\\ \rho(A_{13})= \tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \sigma_z,&\rho(A_{27})=\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes I,\\ \rho(A_{14})= \tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes I,&\rho(A_{28})=\tfrac12 \sigma_z \otimes \sigma_z\otimes I\otimes I. \end{array} \end{align} $$
Looking at the first factor in all of these generators, we observe that it is either I or
![]() $\sigma _z$
, (i.e., it is diagonal). This means that this 16-dimensional representation of
$\sigma _z$
, (i.e., it is diagonal). This means that this 16-dimensional representation of
![]() $\mathbb {R}\oplus \mathfrak {so}(4,4)$
is reducible. It splits onto two real
$\mathbb {R}\oplus \mathfrak {so}(4,4)$
is reducible. It splits onto two real
![]() $8$
-dimensional Weyl representations
$8$
-dimensional Weyl representations
in the spaces
![]() $S_\pm $
of (Majorana)-Weyl spinors.
$S_\pm $
of (Majorana)-Weyl spinors.
On generators of
![]() $\mathfrak {so}(4,4)$
, these two 8-dimensional representations
$\mathfrak {so}(4,4)$
, these two 8-dimensional representations
![]() $\rho _\pm $
are given by
$\rho _\pm $
are given by
 $$ \begin{align} \begin{array}{ll} \rho_\pm(A_1)= \tfrac12 I\otimes I\otimes \sigma_z,&\rho_\pm(A_{15})=\tfrac12 \sigma_z\otimes \sigma_z\otimes I,\\ \rho_\pm(A_2)= \tfrac12 I\otimes I\otimes \epsilon ,&\rho_\pm(A_{16})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_x,\\ \rho_\pm(A_3)= \tfrac12 I\otimes I\otimes \sigma_x ,&\rho_\pm(A_{17})=\tfrac12 \epsilon\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_4)=\tfrac12 I\otimes \sigma_z\otimes \sigma_x,&\rho_\pm(A_{18})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho_\pm(A_5)= \tfrac12 I\otimes \sigma_z\otimes \epsilon,&\rho_\pm(A_{19})=\tfrac12 \epsilon\otimes \epsilon\otimes I ,\\ \rho_\pm(A_6)= \tfrac12 I\otimes \sigma_z\otimes \sigma_z,&\rho_\pm(A_{20})=\tfrac12 \epsilon\otimes \sigma_z\otimes I ,\\ \rho_\pm(A_7)= \tfrac12 I\otimes \epsilon\otimes \sigma_x,&\rho_\pm(A_{21})=\tfrac12 \sigma_x\otimes I\otimes I,\\ \rho_\pm(A_8)= \tfrac12 I\otimes \epsilon\otimes \epsilon,&\rho_\pm(A_{22})=\pm\tfrac12 \sigma_x\otimes \sigma_x\otimes \sigma_x ,\\ \rho_\pm(A_9)= \tfrac12 I\otimes \epsilon\otimes \sigma_z,&\rho_\pm(A_{23})=\pm\tfrac12 \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_{10})=\tfrac12 I\otimes \sigma_x\otimes I,&\rho_\pm(A_{24})=\pm\tfrac12 \sigma_x\otimes \sigma_x\otimes \sigma_z ,\\ \rho_\pm(A_{11})= \tfrac12 \sigma_z\otimes \sigma_x\otimes \sigma_x ,&\rho_\pm(A_{25})=\pm\tfrac12 \sigma_x\otimes \epsilon\otimes I ,\\ \rho_\pm(A_{12})= \tfrac12 \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho_\pm(A_{26})=\pm\tfrac12 \sigma_x\otimes \sigma_z\otimes I ,\\ \rho_\pm(A_{13})= \tfrac12 \sigma_z\otimes \sigma_x\otimes \sigma_z,&\rho_\pm(A_{27})=\pm\tfrac12 \epsilon\otimes I\otimes I,\\ \rho_\pm(A_{14})= \tfrac12 \sigma_z\otimes \epsilon\otimes I,&\rho_\pm(A_{28})=\pm\tfrac12 \sigma_z\otimes I\otimes I. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \rho_\pm(A_1)= \tfrac12 I\otimes I\otimes \sigma_z,&\rho_\pm(A_{15})=\tfrac12 \sigma_z\otimes \sigma_z\otimes I,\\ \rho_\pm(A_2)= \tfrac12 I\otimes I\otimes \epsilon ,&\rho_\pm(A_{16})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_x,\\ \rho_\pm(A_3)= \tfrac12 I\otimes I\otimes \sigma_x ,&\rho_\pm(A_{17})=\tfrac12 \epsilon\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_4)=\tfrac12 I\otimes \sigma_z\otimes \sigma_x,&\rho_\pm(A_{18})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho_\pm(A_5)= \tfrac12 I\otimes \sigma_z\otimes \epsilon,&\rho_\pm(A_{19})=\tfrac12 \epsilon\otimes \epsilon\otimes I ,\\ \rho_\pm(A_6)= \tfrac12 I\otimes \sigma_z\otimes \sigma_z,&\rho_\pm(A_{20})=\tfrac12 \epsilon\otimes \sigma_z\otimes I ,\\ \rho_\pm(A_7)= \tfrac12 I\otimes \epsilon\otimes \sigma_x,&\rho_\pm(A_{21})=\tfrac12 \sigma_x\otimes I\otimes I,\\ \rho_\pm(A_8)= \tfrac12 I\otimes \epsilon\otimes \epsilon,&\rho_\pm(A_{22})=\pm\tfrac12 \sigma_x\otimes \sigma_x\otimes \sigma_x ,\\ \rho_\pm(A_9)= \tfrac12 I\otimes \epsilon\otimes \sigma_z,&\rho_\pm(A_{23})=\pm\tfrac12 \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_{10})=\tfrac12 I\otimes \sigma_x\otimes I,&\rho_\pm(A_{24})=\pm\tfrac12 \sigma_x\otimes \sigma_x\otimes \sigma_z ,\\ \rho_\pm(A_{11})= \tfrac12 \sigma_z\otimes \sigma_x\otimes \sigma_x ,&\rho_\pm(A_{25})=\pm\tfrac12 \sigma_x\otimes \epsilon\otimes I ,\\ \rho_\pm(A_{12})= \tfrac12 \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho_\pm(A_{26})=\pm\tfrac12 \sigma_x\otimes \sigma_z\otimes I ,\\ \rho_\pm(A_{13})= \tfrac12 \sigma_z\otimes \sigma_x\otimes \sigma_z,&\rho_\pm(A_{27})=\pm\tfrac12 \epsilon\otimes I\otimes I,\\ \rho_\pm(A_{14})= \tfrac12 \sigma_z\otimes \epsilon\otimes I,&\rho_\pm(A_{28})=\pm\tfrac12 \sigma_z\otimes I\otimes I. \end{array} \end{align} $$
We extend them to
![]() $\mathbb {R}\oplus \mathfrak {so}(4,4)$
by adding
$\mathbb {R}\oplus \mathfrak {so}(4,4)$
by adding
It follows that the Weyl representations
![]() $(\rho _\pm ,S_\pm )$
of
$(\rho _\pm ,S_\pm )$
of
![]() $\mathfrak {so}(4,4)$
are irreducible and nonequivalent.
$\mathfrak {so}(4,4)$
are irreducible and nonequivalent.
They can be used to find yet another real 8-dimensional representation of
![]() $\mathfrak {so}(4,4)$
. For this, one considers the tensor product representation
$\mathfrak {so}(4,4)$
. For this, one considers the tensor product representation
This 64-dimensional real representation of
![]() $\mathfrak {so}(4,4)$
is reducible. It decomposes as
$\mathfrak {so}(4,4)$
is reducible. It decomposes as
having irreducible components
![]() $(\alpha ,T_{56})$
and
$(\alpha ,T_{56})$
and
![]() $(\tau ,R)$
of respective dimensions 56 and 8. Explicitly, on generators of
$(\tau ,R)$
of respective dimensions 56 and 8. Explicitly, on generators of
![]() $\mathbb {R}\oplus \mathfrak {so}(4,4)$
, the 8-dimensional representation
$\mathbb {R}\oplus \mathfrak {so}(4,4)$
, the 8-dimensional representation
![]() $\tau $
reads
$\tau $
reads
 $$ \begin{align}\begin{aligned}
&\tau(A_1)=E_{66}-E_{22},\\
&\tau(A_2)=\tfrac12(E_{23}-E_{32}+E_{25}-E_{52}+E_{36}-E_{63}+E_{56}-E_{65}),\\
&\tau(A_3)=\tfrac12(E_{23}+E_{32}+E_{25}+E_{52}+E_{36}+E_{63}+E_{56}+E_{65}),\\
&\tau(A_4)=\tfrac12(E_{23}+E_{32}-E_{25}-E_{52}-E_{36}-E_{63}+E_{56}+E_{65}),\\
&\tau(A_5)=\tfrac12(E_{23}-E_{32}-E_{25}+E_{52}-E_{36}+E_{63}+E_{56}-E_{65}),\\
&\tau(A_6)=E_{33}-E_{55},\\
&\tau(A_7)=\tfrac12(E_{12}-E_{21}-E_{16}+E_{61}-E_{27}+E_{72}+E_{67}-E_{76}),\\
&\tau(A_8)=\tfrac12(-E_{12}-E_{21}-E_{16}-E_{61}-E_{27}-E_{72}-E_{67}-E_{76}),\\
&\tau(A_9)=\tfrac12(E_{13}-E_{31}+E_{15}-E_{51}-E_{37}+E_{73}-E_{57}+E_{75}),\\
&\tau(A_{10})=\tfrac12(E_{13}+E_{31}-E_{15}-E_{51}+E_{37}+E_{73}-E_{57}-E_{75}),\\
&\tau(A_{11})=\tfrac12(-E_{12}-E_{21}+E_{16}+E_{61}+E_{27}+E_{72}-E_{67}-E_{76}),\\
&\tau(A_{12})=\tfrac12(E_{12}-E_{21}+E_{16}-E_{61}+E_{27}-E_{72}+E_{67}-E_{76}),\\
&\tau(A_{13})=\tfrac12(-E_{13}-E_{31}-E_{15}-E_{51}+E_{37}+E_{73}+E_{57}+E_{75}),\\
&\tau(A_{14})=\tfrac12(-E_{13}+E_{31}+E_{15}-E_{51}-E_{37}+E_{73}+E_{57}-E_{75}),\\
&\tau(A_{15})=E_{11}-E_{77},\\
&\tau(A_{16})=\tfrac12(E_{24}-E_{42}+E_{28}-E_{82}+E_{46}-E_{64}-E_{68}+E_{86}),\\
&\tau(A_{17})=\tfrac12(E_{24}+E_{42}+E_{28}+E_{82}+E_{46}+E_{64}+E_{68}+E_{86}),\\
&\tau(A_{18})=\tfrac12(E_{34}-E_{43}+E_{38}-E_{83}-E_{45}+E_{54}+E_{58}-E_{85}),\\
&\tau(A_{19})=\tfrac12(-E_{34}-E_{43}-E_{38}-E_{83}+E_{45}+E_{54}+E_{58}+E_{85}),\\
&\tau(A_{20})=\tfrac12(-E_{14}+E_{41}-E_{18}+E_{81}+E_{47}-E_{74}-E_{78}+E_{87}),\\
&\tau(A_{21})=\tfrac12(E_{14}+E_{41}+E_{18}+E_{81}-E_{47}-E_{74}-E_{78}-E_{87}),\\
&\tau(A_{22})=\tfrac12(-E_{24}-E_{42}+E_{28}+E_{82}+E_{46}+E_{64}-E_{68}-E_{86}),\\
&\tau(A_{23})=\tfrac12(-E_{24}+E_{42}+E_{28}-E_{82}+E_{46}-E_{64}+E_{68}-E_{86}),\\
&\tau(A_{24})=\tfrac12(-E_{34}-E_{43}+E_{38}+E_{83}-E_{45}-E_{54}+E_{58}+E_{85}),\\
&\tau(A_{25})=\tfrac12(E_{34}-E_{43}-E_{38}+E_{83}+E_{45}-E_{54}+E_{58}-E_{85}),\\
&\tau(A_{26})=\tfrac12(E_{14}+E_{41}-E_{18}-E_{81}+E_{47}+E_{74}-E_{78}-E_{87}),\\
&\tau(A_{27})=\tfrac12(-E_{14}+E_{41}+E_{18}-E_{81}-E_{47}+E_{74}-E_{78}+E_{87}),\\
&\tau(A_{28})=-E_{44}+E_{88},\\
&\tau(A_{29})=E_{11}+E_{22}+E_{33}+E_{44}+E_{55}+E_{66}+E_{77}+E_{88}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned}
&\tau(A_1)=E_{66}-E_{22},\\
&\tau(A_2)=\tfrac12(E_{23}-E_{32}+E_{25}-E_{52}+E_{36}-E_{63}+E_{56}-E_{65}),\\
&\tau(A_3)=\tfrac12(E_{23}+E_{32}+E_{25}+E_{52}+E_{36}+E_{63}+E_{56}+E_{65}),\\
&\tau(A_4)=\tfrac12(E_{23}+E_{32}-E_{25}-E_{52}-E_{36}-E_{63}+E_{56}+E_{65}),\\
&\tau(A_5)=\tfrac12(E_{23}-E_{32}-E_{25}+E_{52}-E_{36}+E_{63}+E_{56}-E_{65}),\\
&\tau(A_6)=E_{33}-E_{55},\\
&\tau(A_7)=\tfrac12(E_{12}-E_{21}-E_{16}+E_{61}-E_{27}+E_{72}+E_{67}-E_{76}),\\
&\tau(A_8)=\tfrac12(-E_{12}-E_{21}-E_{16}-E_{61}-E_{27}-E_{72}-E_{67}-E_{76}),\\
&\tau(A_9)=\tfrac12(E_{13}-E_{31}+E_{15}-E_{51}-E_{37}+E_{73}-E_{57}+E_{75}),\\
&\tau(A_{10})=\tfrac12(E_{13}+E_{31}-E_{15}-E_{51}+E_{37}+E_{73}-E_{57}-E_{75}),\\
&\tau(A_{11})=\tfrac12(-E_{12}-E_{21}+E_{16}+E_{61}+E_{27}+E_{72}-E_{67}-E_{76}),\\
&\tau(A_{12})=\tfrac12(E_{12}-E_{21}+E_{16}-E_{61}+E_{27}-E_{72}+E_{67}-E_{76}),\\
&\tau(A_{13})=\tfrac12(-E_{13}-E_{31}-E_{15}-E_{51}+E_{37}+E_{73}+E_{57}+E_{75}),\\
&\tau(A_{14})=\tfrac12(-E_{13}+E_{31}+E_{15}-E_{51}-E_{37}+E_{73}+E_{57}-E_{75}),\\
&\tau(A_{15})=E_{11}-E_{77},\\
&\tau(A_{16})=\tfrac12(E_{24}-E_{42}+E_{28}-E_{82}+E_{46}-E_{64}-E_{68}+E_{86}),\\
&\tau(A_{17})=\tfrac12(E_{24}+E_{42}+E_{28}+E_{82}+E_{46}+E_{64}+E_{68}+E_{86}),\\
&\tau(A_{18})=\tfrac12(E_{34}-E_{43}+E_{38}-E_{83}-E_{45}+E_{54}+E_{58}-E_{85}),\\
&\tau(A_{19})=\tfrac12(-E_{34}-E_{43}-E_{38}-E_{83}+E_{45}+E_{54}+E_{58}+E_{85}),\\
&\tau(A_{20})=\tfrac12(-E_{14}+E_{41}-E_{18}+E_{81}+E_{47}-E_{74}-E_{78}+E_{87}),\\
&\tau(A_{21})=\tfrac12(E_{14}+E_{41}+E_{18}+E_{81}-E_{47}-E_{74}-E_{78}-E_{87}),\\
&\tau(A_{22})=\tfrac12(-E_{24}-E_{42}+E_{28}+E_{82}+E_{46}+E_{64}-E_{68}-E_{86}),\\
&\tau(A_{23})=\tfrac12(-E_{24}+E_{42}+E_{28}-E_{82}+E_{46}-E_{64}+E_{68}-E_{86}),\\
&\tau(A_{24})=\tfrac12(-E_{34}-E_{43}+E_{38}+E_{83}-E_{45}-E_{54}+E_{58}+E_{85}),\\
&\tau(A_{25})=\tfrac12(E_{34}-E_{43}-E_{38}+E_{83}+E_{45}-E_{54}+E_{58}-E_{85}),\\
&\tau(A_{26})=\tfrac12(E_{14}+E_{41}-E_{18}-E_{81}+E_{47}+E_{74}-E_{78}-E_{87}),\\
&\tau(A_{27})=\tfrac12(-E_{14}+E_{41}+E_{18}-E_{81}-E_{47}+E_{74}-E_{78}+E_{87}),\\
&\tau(A_{28})=-E_{44}+E_{88},\\
&\tau(A_{29})=E_{11}+E_{22}+E_{33}+E_{44}+E_{55}+E_{66}+E_{77}+E_{88}, \end{aligned}\end{align} $$
where
![]() $E_{ij}$
,
$E_{ij}$
,
![]() $i,j=1,2,\dots ,8$
denote
$i,j=1,2,\dots ,8$
denote
![]() $8\times 8$
matrices with zeroes everywhere except the value 1 in the entry
$8\times 8$
matrices with zeroes everywhere except the value 1 in the entry
![]() $(i,j)$
seating at the crossing of the ith row and the jth column.
$(i,j)$
seating at the crossing of the ith row and the jth column.
The three real, irreducible, pairwise nonequivalent representations
![]() $(\rho _+,\rho _-,\tau )$
of
$(\rho _+,\rho _-,\tau )$
of
![]() $\mathfrak {so}(4,4)$
, given by the formulas (9.4) and (9.5), constitute the set of the triality representations for
$\mathfrak {so}(4,4)$
, given by the formulas (9.4) and (9.5), constitute the set of the triality representations for
![]() $\mathfrak {so}(4,4)$
.
$\mathfrak {so}(4,4)$
.
9.2. Triality representations of
 $\mathfrak {so}(8,0)$
$\mathfrak {so}(8,0)$
To get the real representation
![]() $(\rho ,S)$
of
$(\rho ,S)$
of
![]() $\mathfrak {so}(8,0)$
in the space
$\mathfrak {so}(8,0)$
in the space
![]() $S=\mathbb {R}^{16}$
of Dirac spinors, we need the real Dirac
$S=\mathbb {R}^{16}$
of Dirac spinors, we need the real Dirac
![]() $\gamma $
matrices satisfying the Dirac identity (9.2), but now with
$\gamma $
matrices satisfying the Dirac identity (9.2), but now with
where
![]() $\delta _{ij}$
is the Kronecker delta in 8 dimensions.
$\delta _{ij}$
is the Kronecker delta in 8 dimensions.
Thus, we need to modify the Dirac matrices
![]() $\gamma _i$
from (9.1) to have the proper signature of the metric. This is done in two steps [Reference Trautman, Naber, Tsou and Françoise19]. First, one puts the imaginary unit i in front of some of the Dirac matrices
$\gamma _i$
from (9.1) to have the proper signature of the metric. This is done in two steps [Reference Trautman, Naber, Tsou and Françoise19]. First, one puts the imaginary unit i in front of some of the Dirac matrices
![]() $\gamma _i$
generating the Clifford algebra
$\gamma _i$
generating the Clifford algebra
![]() ${\mathcal C}\ell (4,4)$
to get the proper signature of
${\mathcal C}\ell (4,4)$
to get the proper signature of
![]() $(g_{ij})$
. Although this produces few complex generators, in step two, one uses them with the others and modifies them in an algorithmic fashion so that they become all real and still satisfy the Dirac identity with the proper signature of
$(g_{ij})$
. Although this produces few complex generators, in step two, one uses them with the others and modifies them in an algorithmic fashion so that they become all real and still satisfy the Dirac identity with the proper signature of
![]() $(g_{ij})$
. Explicitly, it is done as follows:
$(g_{ij})$
. Explicitly, it is done as follows:
By placing the imaginary unit i in front of
![]() $\gamma _2$
,
$\gamma _2$
,
![]() $\gamma _4$
,
$\gamma _4$
,
![]() $\gamma _6$
and
$\gamma _6$
and
![]() $\gamma _8$
in (9.1), we obtain 8 matrices
$\gamma _8$
in (9.1), we obtain 8 matrices
with
![]() $\gamma _i$
,
$\gamma _i$
,
![]() $i,1,\dots ,8$
, in (9.1). These constitute generators of the complex 16-dimensional representation of the Clifford algebra
$i,1,\dots ,8$
, in (9.1). These constitute generators of the complex 16-dimensional representation of the Clifford algebra
![]() ${\mathcal C}\ell (8,0)$
. We will also need the representation of this Clifford algebra, which is complex conjugate of
${\mathcal C}\ell (8,0)$
. We will also need the representation of this Clifford algebra, which is complex conjugate of
![]() $\tilde {\gamma }$
. This is generated by
$\tilde {\gamma }$
. This is generated by
The Clifford algebra representations generated by the Dirac matrices
![]() $\tilde {\gamma }$
and
$\tilde {\gamma }$
and
![]() $\overline {\tilde {\gamma }}$
are real equivalent – that is, there exists a real
$\overline {\tilde {\gamma }}$
are real equivalent – that is, there exists a real
![]() $16\times 16$
matrix B such that
$16\times 16$
matrix B such that
It can be chosen so that
where
![]() $\mathrm {Id}=I\otimes I\otimes I\otimes I$
.
$\mathrm {Id}=I\otimes I\otimes I\otimes I$
.
Explicitly,
Using this matrix, we define a new set of eight
![]() $\gamma $
matricesFootnote
6
by
$\gamma $
matricesFootnote
6
by
One can check that these 8 matrices are all real and that they satisfy the desired Dirac identity:
Explicitly, we have
 $$ \begin{align*}\begin{aligned} &\gamma_1=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_x\\ &\gamma_2=-\epsilon\otimes\sigma_z\otimes\epsilon\otimes I\\ &\gamma_3=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_z\\ &\gamma_4=\epsilon\otimes\sigma_z\otimes\sigma_x\otimes \epsilon\\ &\gamma_5=\sigma_x\otimes\sigma_x\otimes\sigma_z\otimes I\\ &\gamma_6=-\epsilon\otimes I\otimes \sigma_z\otimes \epsilon\\ &\gamma_7=\sigma_x\otimes\sigma_z\otimes I\otimes I\\ &\gamma_8=\sigma_x\otimes \epsilon\otimes \sigma_z\otimes \epsilon. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\gamma_1=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_x\\ &\gamma_2=-\epsilon\otimes\sigma_z\otimes\epsilon\otimes I\\ &\gamma_3=\sigma_x\otimes\sigma_x\otimes\sigma_x\otimes\sigma_z\\ &\gamma_4=\epsilon\otimes\sigma_z\otimes\sigma_x\otimes \epsilon\\ &\gamma_5=\sigma_x\otimes\sigma_x\otimes\sigma_z\otimes I\\ &\gamma_6=-\epsilon\otimes I\otimes \sigma_z\otimes \epsilon\\ &\gamma_7=\sigma_x\otimes\sigma_z\otimes I\otimes I\\ &\gamma_8=\sigma_x\otimes \epsilon\otimes \sigma_z\otimes \epsilon. \end{aligned} \end{align*} $$
The 28 generators of
![]() $\mathfrak {so}(8,0)$
in the Majorana-Dirac spinor representation
$\mathfrak {so}(8,0)$
in the Majorana-Dirac spinor representation
![]() $\rho $
in the space of Dirac spinors
$\rho $
in the space of Dirac spinors
![]() $S=\mathbb {R}^{16}$
are given by
$S=\mathbb {R}^{16}$
are given by
where again we have used the function
![]() $I=I(i,j)$
defined in (8.1). Note that since now
$I=I(i,j)$
defined in (8.1). Note that since now
![]() $i<j$
can run from 1 to 8, the function has a range from 1 to 28. We add to this the scaling generator,
$i<j$
can run from 1 to 8, the function has a range from 1 to 28. We add to this the scaling generator,
![]() $\rho (A_{29})$
, extending the Lie algebra
$\rho (A_{29})$
, extending the Lie algebra
![]() $\mathfrak {so}(4,4)$
to
$\mathfrak {so}(4,4)$
to
![]() $\mathfrak {coa}(4,4)$
, given by
$\mathfrak {coa}(4,4)$
, given by
In terms of the 2-dimensional Pauli matrices, these generators look like
 $$ \begin{align} \begin{array}{ll} \rho(A_1)= -\tfrac12 \sigma_z \otimes \epsilon\otimes \sigma_z\otimes \sigma_x,&\rho(A_{15})=-\tfrac12 \sigma_z \otimes \sigma_x\otimes I\otimes \epsilon,\\ \rho(A_2)= \tfrac12 I \otimes I\otimes I\otimes \epsilon ,&\rho(A_{16})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_x,\\ \rho(A_3)= \tfrac12 \sigma_z \otimes \epsilon\otimes \sigma_z\otimes \sigma_z ,&\rho(A_{17})=\tfrac12 \sigma_z \otimes I \otimes \epsilon\otimes I ,\\ \rho(A_4)=\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes \sigma_z,&\rho(A_{18})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho(A_5)= -\tfrac12 I \otimes I\otimes \sigma_z\otimes \epsilon,&\rho(A_{19})=-\tfrac12 \sigma_z \otimes I\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_6)= -\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes \sigma_x,&\rho(A_{20})=\tfrac12 I \otimes \epsilon\otimes \sigma_z\otimes I ,\\ \rho(A_7)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_x,&\rho(A_{21})=\tfrac12 \sigma_z \otimes \sigma_z\otimes \sigma_z\otimes \epsilon,\\ \rho(A_8)= -\tfrac12 \sigma_z \otimes \epsilon\otimes \sigma_x\otimes I,&\rho(A_{22})=\tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes \sigma_z ,\\ \rho(A_9)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_z,&\rho(A_{23})=-\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_{10})=\tfrac12 \sigma_z \otimes \epsilon\otimes \epsilon\otimes \epsilon,&\rho(A_{24})=-\tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes \sigma_x ,\\ \rho(A_{11})= -\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes \sigma_z ,&\rho(A_{25})=-\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes I ,\\ \rho(A_{12})= -\tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho(A_{26})=\tfrac12 I \otimes \sigma_z\otimes I\otimes \epsilon ,\\ \rho(A_{13})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes \sigma_x,&\rho(A_{27})=-\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes I,\\ \rho(A_{14})= -\tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes I,&\rho(A_{28})=-\tfrac12 I \otimes \sigma_x\otimes \sigma_z\otimes \epsilon. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \rho(A_1)= -\tfrac12 \sigma_z \otimes \epsilon\otimes \sigma_z\otimes \sigma_x,&\rho(A_{15})=-\tfrac12 \sigma_z \otimes \sigma_x\otimes I\otimes \epsilon,\\ \rho(A_2)= \tfrac12 I \otimes I\otimes I\otimes \epsilon ,&\rho(A_{16})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_x,\\ \rho(A_3)= \tfrac12 \sigma_z \otimes \epsilon\otimes \sigma_z\otimes \sigma_z ,&\rho(A_{17})=\tfrac12 \sigma_z \otimes I \otimes \epsilon\otimes I ,\\ \rho(A_4)=\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes \sigma_z,&\rho(A_{18})=\tfrac12 I \otimes \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho(A_5)= -\tfrac12 I \otimes I\otimes \sigma_z\otimes \epsilon,&\rho(A_{19})=-\tfrac12 \sigma_z \otimes I\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_6)= -\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes \sigma_x,&\rho(A_{20})=\tfrac12 I \otimes \epsilon\otimes \sigma_z\otimes I ,\\ \rho(A_7)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_x,&\rho(A_{21})=\tfrac12 \sigma_z \otimes \sigma_z\otimes \sigma_z\otimes \epsilon,\\ \rho(A_8)= -\tfrac12 \sigma_z \otimes \epsilon\otimes \sigma_x\otimes I,&\rho(A_{22})=\tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes \sigma_z ,\\ \rho(A_9)= \tfrac12 I \otimes I\otimes \epsilon\otimes \sigma_z,&\rho(A_{23})=-\tfrac12 \sigma_z \otimes \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho(A_{10})=\tfrac12 \sigma_z \otimes \epsilon\otimes \epsilon\otimes \epsilon,&\rho(A_{24})=-\tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes \sigma_x ,\\ \rho(A_{11})= -\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes \sigma_z ,&\rho(A_{25})=-\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes I ,\\ \rho(A_{12})= -\tfrac12 I \otimes \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho(A_{26})=\tfrac12 I \otimes \sigma_z\otimes I\otimes \epsilon ,\\ \rho(A_{13})=\tfrac12 \sigma_z \otimes \sigma_x\otimes \epsilon\otimes \sigma_x,&\rho(A_{27})=-\tfrac12 \sigma_z \otimes \epsilon\otimes I\otimes I,\\ \rho(A_{14})= -\tfrac12 I \otimes \sigma_z\otimes \epsilon\otimes I,&\rho(A_{28})=-\tfrac12 I \otimes \sigma_x\otimes \sigma_z\otimes \epsilon. \end{array} \end{align} $$
Similarly, as in the case of
![]() $\mathfrak {so}(4,4)$
, this 16-dimensional representation of
$\mathfrak {so}(4,4)$
, this 16-dimensional representation of
![]() $\mathbb {R}\oplus \mathfrak {so}(4,4)$
is reducible, again due to the appearance of I and
$\mathbb {R}\oplus \mathfrak {so}(4,4)$
is reducible, again due to the appearance of I and
![]() $\sigma _z$
only as the first factors in the above formulas. It splits onto two real
$\sigma _z$
only as the first factors in the above formulas. It splits onto two real
![]() $8$
-dimensional Weyl representations
$8$
-dimensional Weyl representations
On generators of
![]() $\mathfrak {so}(8,0)$
, these two 8-dimensional representations
$\mathfrak {so}(8,0)$
, these two 8-dimensional representations
![]() $\rho _\pm $
, are given by
$\rho _\pm $
, are given by
 $$ \begin{align} \begin{array}{ll}
\rho_\pm(A_1)= \mp\tfrac12 \epsilon\otimes \sigma_z\otimes \sigma_x,&\rho_\pm(A_{15})=\mp\tfrac12 \sigma_x\otimes I\otimes \epsilon,\\
\rho_\pm(A_2)= \tfrac12 I\otimes I\otimes \epsilon ,&\rho_\pm(A_{16})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_x,\\
\rho_\pm(A_3)= \pm\tfrac12 \epsilon\otimes \sigma_z\otimes \sigma_z ,&\rho_\pm(A_{17})=\pm\tfrac12 I \otimes \epsilon\otimes I ,\\
\rho_\pm(A_4)=\pm\tfrac12 \epsilon\otimes I\otimes \sigma_z,&\rho_\pm(A_{18})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho_\pm(A_5)= -\tfrac12 I\otimes \sigma_z\otimes \epsilon,&\rho_\pm(A_{19})=\mp\tfrac12 I\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_6)= \mp\tfrac12 \epsilon\otimes I\otimes \sigma_x,&\rho_\pm(A_{20})=\tfrac12 \epsilon\otimes \sigma_z\otimes I ,\\ \rho_\pm(A_7)= \tfrac12 I\otimes \epsilon\otimes \sigma_x,&\rho_\pm(A_{21})=\pm\tfrac12 \sigma_z\otimes \sigma_z\otimes \epsilon,\\ \rho_\pm(A_8)= \mp\tfrac12 \epsilon\otimes \sigma_x\otimes I,&\rho_\pm(A_{22})=\tfrac12 \sigma_z\otimes \epsilon\otimes \sigma_z ,\\ \rho_\pm(A_9)= \tfrac12 I\otimes \epsilon\otimes \sigma_z,&\rho_\pm(A_{23})=\mp\tfrac12 \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_{10})=\pm\tfrac12 \epsilon\otimes \epsilon\otimes \epsilon,&\rho_\pm(A_{24})=-\tfrac12 \sigma_z\otimes \epsilon\otimes \sigma_x ,\\ \rho_\pm(A_{11})= \mp\tfrac12 \sigma_x\otimes \epsilon\otimes \sigma_z ,&\rho_\pm(A_{25})=\mp\tfrac12 \sigma_x\otimes \epsilon\otimes I ,\\ \rho_\pm(A_{12})= -\tfrac12 \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho_\pm(A_{26})=\tfrac12 \sigma_z\otimes I\otimes \epsilon ,\\ \rho_\pm(A_{13})=\pm\tfrac12 \sigma_x\otimes \epsilon\otimes \sigma_x,&\rho_\pm(A_{27})=\mp\tfrac12 \epsilon\otimes I\otimes I,\\ \rho_\pm(A_{14})= -\tfrac12 \sigma_z\otimes \epsilon\otimes I,&\rho_\pm(A_{28})=-\tfrac12 \sigma_x\otimes \sigma_z\otimes \epsilon.
\end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll}
\rho_\pm(A_1)= \mp\tfrac12 \epsilon\otimes \sigma_z\otimes \sigma_x,&\rho_\pm(A_{15})=\mp\tfrac12 \sigma_x\otimes I\otimes \epsilon,\\
\rho_\pm(A_2)= \tfrac12 I\otimes I\otimes \epsilon ,&\rho_\pm(A_{16})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_x,\\
\rho_\pm(A_3)= \pm\tfrac12 \epsilon\otimes \sigma_z\otimes \sigma_z ,&\rho_\pm(A_{17})=\pm\tfrac12 I \otimes \epsilon\otimes I ,\\
\rho_\pm(A_4)=\pm\tfrac12 \epsilon\otimes I\otimes \sigma_z,&\rho_\pm(A_{18})=\tfrac12 \epsilon\otimes \sigma_x\otimes \sigma_z ,\\ \rho_\pm(A_5)= -\tfrac12 I\otimes \sigma_z\otimes \epsilon,&\rho_\pm(A_{19})=\mp\tfrac12 I\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_6)= \mp\tfrac12 \epsilon\otimes I\otimes \sigma_x,&\rho_\pm(A_{20})=\tfrac12 \epsilon\otimes \sigma_z\otimes I ,\\ \rho_\pm(A_7)= \tfrac12 I\otimes \epsilon\otimes \sigma_x,&\rho_\pm(A_{21})=\pm\tfrac12 \sigma_z\otimes \sigma_z\otimes \epsilon,\\ \rho_\pm(A_8)= \mp\tfrac12 \epsilon\otimes \sigma_x\otimes I,&\rho_\pm(A_{22})=\tfrac12 \sigma_z\otimes \epsilon\otimes \sigma_z ,\\ \rho_\pm(A_9)= \tfrac12 I\otimes \epsilon\otimes \sigma_z,&\rho_\pm(A_{23})=\mp\tfrac12 \sigma_x\otimes \sigma_x\otimes \epsilon ,\\ \rho_\pm(A_{10})=\pm\tfrac12 \epsilon\otimes \epsilon\otimes \epsilon,&\rho_\pm(A_{24})=-\tfrac12 \sigma_z\otimes \epsilon\otimes \sigma_x ,\\ \rho_\pm(A_{11})= \mp\tfrac12 \sigma_x\otimes \epsilon\otimes \sigma_z ,&\rho_\pm(A_{25})=\mp\tfrac12 \sigma_x\otimes \epsilon\otimes I ,\\ \rho_\pm(A_{12})= -\tfrac12 \sigma_z\otimes \sigma_x\otimes \epsilon,&\rho_\pm(A_{26})=\tfrac12 \sigma_z\otimes I\otimes \epsilon ,\\ \rho_\pm(A_{13})=\pm\tfrac12 \sigma_x\otimes \epsilon\otimes \sigma_x,&\rho_\pm(A_{27})=\mp\tfrac12 \epsilon\otimes I\otimes I,\\ \rho_\pm(A_{14})= -\tfrac12 \sigma_z\otimes \epsilon\otimes I,&\rho_\pm(A_{28})=-\tfrac12 \sigma_x\otimes \sigma_z\otimes \epsilon.
\end{array} \end{align} $$
We extend them em to
![]() $\mathbb {R}\oplus \mathfrak {so}(8,0)$
by adding
$\mathbb {R}\oplus \mathfrak {so}(8,0)$
by adding
It follows that the Weyl representations
![]() $(\rho _\pm ,S_\pm )$
of
$(\rho _\pm ,S_\pm )$
of
![]() $\mathfrak {so}(4,4)$
are irreducible and nonequivalent.
$\mathfrak {so}(4,4)$
are irreducible and nonequivalent.
We use them to find the defining representation
![]() $(\tau ,R)$
of
$(\tau ,R)$
of
![]() $\mathfrak {so}(8,0)$
in the vector space
$\mathfrak {so}(8,0)$
in the vector space
![]() $R=\mathbb {R}^8$
of vectors. We again consider the tensor product representation
$R=\mathbb {R}^8$
of vectors. We again consider the tensor product representation
![]() $\rho _+\otimes \rho _-$
. It decomposes as
$\rho _+\otimes \rho _-$
. It decomposes as
having irreducible components
![]() $(\alpha ,T_{56})$
and
$(\alpha ,T_{56})$
and
![]() $(\tau ,R)$
of respective dimensions 56 and 8. Explicitly, on generators
$(\tau ,R)$
of respective dimensions 56 and 8. Explicitly, on generators
![]() $A_I$
of
$A_I$
of
![]() $\mathbb {R}\oplus \mathfrak {so}(8,0)$
, the 8-dimensional representation
$\mathbb {R}\oplus \mathfrak {so}(8,0)$
, the 8-dimensional representation
![]() $\tau $
reads
$\tau $
reads
 $$ \begin{align} \begin{array}{llll} \tau(A_1)=E_{38}-E_{83},&\quad \tau(A_8)=E_{35}-E_{53},&\quad \tau(A_{15})=E_{52}-E_{25},&\quad \tau(A_{22})=E_{68}-E_{86},\\ \tau(A_2)=E_{78}-E_{87}, &\quad\tau(A_9)=E_{75}-E_{57}, &\quad \tau(A_{16})=E_{18}-E_{81},&\quad \tau(A_{23})=E_{36}-E_{63}, \\ \tau(A_3)=E_{37}-E_{73}, &\quad\tau(A_{10})=E_{54}-E_{45},&\quad \tau(A_{17})=E_{31}-E_{13},&\quad \tau(A_{24})=E_{76}-E_{67},\\ \tau(A_4)=E_{84}-E_{48},&\quad \tau(A_{11})=E_{28}-E_{82},&\quad \tau(A_{18})=E_{71}-E_{17},&\quad \tau(A_{25})=E_{64}-E_{46},\\ \tau(A_5)=E_{43}-E_{34},&\quad \tau(A_{12})=E_{32}-E_{23},&\quad \tau(A_{19})=E_{14}-E_{41},&\quad \tau(A_{26})=E_{56}-E_{65},\\ \tau(A_6)=E_{47}-E_{74},&\quad \tau(A_{13})=E_{72}-E_{27},&\quad \tau(A_{20})=E_{51}-E_{15},&\quad \tau(A_{27})=E_{26}-E_{62},\\ \tau(A_7)=E_{58}-E_{85}, &\quad \tau(A_{14})= E_{24}-E_{42},&\quad \tau(A_{21})=E_{21}-E_{12},&\quad \tau(A_{28})=E_{16}-E_{61}, \end{array} \end{align} $$
$$ \begin{align} \begin{array}{llll} \tau(A_1)=E_{38}-E_{83},&\quad \tau(A_8)=E_{35}-E_{53},&\quad \tau(A_{15})=E_{52}-E_{25},&\quad \tau(A_{22})=E_{68}-E_{86},\\ \tau(A_2)=E_{78}-E_{87}, &\quad\tau(A_9)=E_{75}-E_{57}, &\quad \tau(A_{16})=E_{18}-E_{81},&\quad \tau(A_{23})=E_{36}-E_{63}, \\ \tau(A_3)=E_{37}-E_{73}, &\quad\tau(A_{10})=E_{54}-E_{45},&\quad \tau(A_{17})=E_{31}-E_{13},&\quad \tau(A_{24})=E_{76}-E_{67},\\ \tau(A_4)=E_{84}-E_{48},&\quad \tau(A_{11})=E_{28}-E_{82},&\quad \tau(A_{18})=E_{71}-E_{17},&\quad \tau(A_{25})=E_{64}-E_{46},\\ \tau(A_5)=E_{43}-E_{34},&\quad \tau(A_{12})=E_{32}-E_{23},&\quad \tau(A_{19})=E_{14}-E_{41},&\quad \tau(A_{26})=E_{56}-E_{65},\\ \tau(A_6)=E_{47}-E_{74},&\quad \tau(A_{13})=E_{72}-E_{27},&\quad \tau(A_{20})=E_{51}-E_{15},&\quad \tau(A_{27})=E_{26}-E_{62},\\ \tau(A_7)=E_{58}-E_{85}, &\quad \tau(A_{14})= E_{24}-E_{42},&\quad \tau(A_{21})=E_{21}-E_{12},&\quad \tau(A_{28})=E_{16}-E_{61}, \end{array} \end{align} $$
where
![]() $E_{ij}$
,
$E_{ij}$
,
![]() $i,j=1,2,\dots ,8$
denote
$i,j=1,2,\dots ,8$
denote
![]() $8\times 8$
matrices with zeroes everywhere except the value 1 in the entry
$8\times 8$
matrices with zeroes everywhere except the value 1 in the entry
![]() $(i,j)$
seating at the crossing of the ith row and the jth column.
$(i,j)$
seating at the crossing of the ith row and the jth column.
The three real, irreducible, pairwise nonequivalent representations
![]() $(\rho _+,\rho _-,\tau )$
of
$(\rho _+,\rho _-,\tau )$
of
![]() $\mathfrak {so}(8,0)$
given by the formulas (9.7) and (9.8) constitute the set of the triality representations for
$\mathfrak {so}(8,0)$
given by the formulas (9.7) and (9.8) constitute the set of the triality representations for
![]() $\mathfrak {so}(8,0)$
.
$\mathfrak {so}(8,0)$
.
10. Application: 2-step graded realisations of real forms of the exceptional Lie algebra
 $\mathfrak {e}_6$
$\mathfrak {e}_6$
The simple exceptional complex Lie algebra
![]() $\mathfrak {e}_6$
has the following noncompact real forms:
$\mathfrak {e}_6$
has the following noncompact real forms:
-
(1)
 $\mathfrak {e}_I$
, with Satake diagram
$\mathfrak {e}_I$
, with Satake diagram  ,
, -
(2)
 $\mathfrak {e}_{II}$
, with Satake diagram
$\mathfrak {e}_{II}$
, with Satake diagram  ,
, -
(3)
 $\mathfrak {e}_{III}$
, with Satake diagram
$\mathfrak {e}_{III}$
, with Satake diagram  , and
, and -
(4)
 $\mathfrak {e}_{IV}$
, with Satake diagram
$\mathfrak {e}_{IV}$
, with Satake diagram  .
.
Èlie Cartan in his theses [Reference Cartan8, Reference Cartan9] mentioned realisation of the real form
![]() $\mathfrak {e}_I$
in
$\mathfrak {e}_I$
in
![]() $N=\mathbb {R}^{16}$
. In the modern language, Cartan’s realisation is such that
$N=\mathbb {R}^{16}$
. In the modern language, Cartan’s realisation is such that
![]() $\mathfrak {e}_I$
is the algebra of authomorphisms of the flat model of a parabolic geometry of type
$\mathfrak {e}_I$
is the algebra of authomorphisms of the flat model of a parabolic geometry of type
![]() $(E_I,P)$
, where the choice of parabolic subgroup in the real form
$(E_I,P)$
, where the choice of parabolic subgroup in the real form
![]() $E_I$
of the exceptional Lie group
$E_I$
of the exceptional Lie group
![]() $\mathbf { E}_6$
is indicated by the following decoration of the Satake diagram for
$\mathbf { E}_6$
is indicated by the following decoration of the Satake diagram for
![]() $\mathfrak {e}_I$
:
$\mathfrak {e}_I$
:  . The structure on the 16-dimensional manifold
. The structure on the 16-dimensional manifold
![]() $N=E_I/P$
, whose symmetry is
$N=E_I/P$
, whose symmetry is
![]() $E_I$
, is a Majorana-Weyl
$E_I$
, is a Majorana-Weyl
![]() $\mathbb {R}\mathbf {Spin}(5,5)$
structure (i.e., the reduction of the structure group of the tangent bundle
$\mathbb {R}\mathbf {Spin}(5,5)$
structure (i.e., the reduction of the structure group of the tangent bundle
![]() $\mathrm {T}N$
to the
$\mathrm {T}N$
to the
![]() $\mathbb {R}\mathbf {Spin}(5,5)\subset \mathbf {GL}(16,\mathbb {R})$
in the irreducible 16-dimensional representation of Majorana-Weyl spinors [Reference Trautman, Naber, Tsou and Françoise19]). This geometry, as 1-step graded, is quite different from 2-step graded geometries considered in our paper. We also mention that if we wanted to have a realisation of, say
$\mathbb {R}\mathbf {Spin}(5,5)\subset \mathbf {GL}(16,\mathbb {R})$
in the irreducible 16-dimensional representation of Majorana-Weyl spinors [Reference Trautman, Naber, Tsou and Françoise19]). This geometry, as 1-step graded, is quite different from 2-step graded geometries considered in our paper. We also mention that if we wanted to have a realisation of, say
![]() $\mathfrak {e}_{II}$
or
$\mathfrak {e}_{II}$
or
![]() $\mathfrak {e}_{III}$
, in the spirit of Cartan’s realisation of
$\mathfrak {e}_{III}$
, in the spirit of Cartan’s realisation of
![]() $\mathfrak {e}_I$
(i.e., if we crossed one lateral node in the Satake diagram of
$\mathfrak {e}_I$
(i.e., if we crossed one lateral node in the Satake diagram of
![]() $\mathfrak {e}_{II}$
or
$\mathfrak {e}_{II}$
or
![]() $\mathfrak {e}_{III}$
), we would be forced to cross the complex conjugated lateral root, resulting in the Satake diagrams
$\mathfrak {e}_{III}$
), we would be forced to cross the complex conjugated lateral root, resulting in the Satake diagrams  or
or  , which would give realisations of the respective
, which would give realisations of the respective
![]() $\mathfrak {e}_{II}$
and
$\mathfrak {e}_{II}$
and
![]() $\mathfrak {e}_{III}$
in dimension twenty four. This we did in [Reference Hill, Merker, Nie and Nurowski14], providing realisations of
$\mathfrak {e}_{III}$
in dimension twenty four. This we did in [Reference Hill, Merker, Nie and Nurowski14], providing realisations of
![]() $\mathfrak {e}_{II}$
and
$\mathfrak {e}_{II}$
and
![]() $\mathfrak {e}_{III}$
as Lie algebras of CR-authomorphisms of certain 24-dimensional CR manifolds of CR dimension 16, and CR (real) codimension 8. The important point of these realisations of these two real forms of
$\mathfrak {e}_{III}$
as Lie algebras of CR-authomorphisms of certain 24-dimensional CR manifolds of CR dimension 16, and CR (real) codimension 8. The important point of these realisations of these two real forms of
![]() $\mathfrak {e}_6$
was that these geometries were 2-step graded, as in the case of Cartan’s realisation of
$\mathfrak {e}_6$
was that these geometries were 2-step graded, as in the case of Cartan’s realisation of
![]() $\mathfrak {f}_I$
, and they could have been also thought as realisations in terms of the symmetry algebras of the structure
$\mathfrak {f}_I$
, and they could have been also thought as realisations in terms of the symmetry algebras of the structure
![]() $(M,{\mathcal D})$
, where M is a certain 24-dimensional real manifold and
$(M,{\mathcal D})$
, where M is a certain 24-dimensional real manifold and
![]() $\mathcal D$
is a real rank 16-distribution on M with
$\mathcal D$
is a real rank 16-distribution on M with
![]() $[{\mathcal D},{\mathcal D}]=\mathrm {T}M$
. Thus, these two geometries described by us in [Reference Hill, Merker, Nie and Nurowski14] are 2-step graded geometries of distributions – very much like Cartan’s realisation of
$[{\mathcal D},{\mathcal D}]=\mathrm {T}M$
. Thus, these two geometries described by us in [Reference Hill, Merker, Nie and Nurowski14] are 2-step graded geometries of distributions – very much like Cartan’s realisation of
![]() $\mathfrak {f}_I$
.
$\mathfrak {f}_I$
.
In this section, we give the remaining similar realisations of the yet untreated cases of
![]() $\mathfrak {e}_{II}$
and
$\mathfrak {e}_{II}$
and
![]() $\mathfrak {e}_{III}$
.
$\mathfrak {e}_{III}$
.
10.1. Realisations of
 $\mathfrak {e}_{I}$
and
$\mathfrak {e}_{I}$
and
 $\mathfrak {e}_{IV}$
: generalities
$\mathfrak {e}_{IV}$
: generalities
To get realisations of
![]() $\mathfrak {e}_{I}$
and
$\mathfrak {e}_{I}$
and
![]() $\mathfrak {e}_{IV}$
in dimension 24, we decorate the Satake diagrams of these two Lie algebras as follows:
$\mathfrak {e}_{IV}$
in dimension 24, we decorate the Satake diagrams of these two Lie algebras as follows:  and
and  . These choices of a parabolic subalgebra in the respective
. These choices of a parabolic subalgebra in the respective
![]() $\mathfrak {e}_{I}$
and
$\mathfrak {e}_{I}$
and
![]() $\mathfrak {e}_{IV}$
produces the following gradation in these algebras:
$\mathfrak {e}_{IV}$
produces the following gradation in these algebras:
with
being 2-step nilpotent and having grading components
![]() $\mathfrak {n}_{-2A}$
and
$\mathfrak {n}_{-2A}$
and ![]() of respective dimension
of respective dimension
![]() $r_A=8$
and
$r_A=8$
and
![]() $s_A=16$
,
$s_A=16$
,
The Lie algebra
![]() $\mathfrak {n}_{0A}$
in the Tanaka prolongation of
$\mathfrak {n}_{0A}$
in the Tanaka prolongation of ![]() up to
up to
![]() $0^{th}$
order is
$0^{th}$
order is
-
(1)
 $\mathfrak {n}_{0I}=2\mathbb {R}\oplus \mathfrak {so}(4,4)=\mathbb {R}\oplus \mathfrak {co}(4,4)$
in the case of
$\mathfrak {n}_{0I}=2\mathbb {R}\oplus \mathfrak {so}(4,4)=\mathbb {R}\oplus \mathfrak {co}(4,4)$
in the case of
 $\mathfrak {e}_I$
, and
$\mathfrak {e}_I$
, and -
(2)
 $\mathfrak {n}_{0IV}=2\mathbb {R}\oplus \mathfrak {so}(8,0)=\mathbb {R}\oplus \mathfrak {co}(8,0)$
in the case of
$\mathfrak {n}_{0IV}=2\mathbb {R}\oplus \mathfrak {so}(8,0)=\mathbb {R}\oplus \mathfrak {co}(8,0)$
in the case of
 $\mathfrak {e}_{IV}$
.
$\mathfrak {e}_{IV}$
.
The last two statements, (1) and (2), get clear when one looks at the Satake diagrams we have just decorated. If we strip off the crossed nodes from these diagrams, we get  and
and  , clearly the simple part of
, clearly the simple part of
![]() $\mathfrak {n}_{0A}$
s above.
$\mathfrak {n}_{0A}$
s above.
Because of the grading property
![]() $[\mathfrak {n}_{iA},\mathfrak {n}_{jA}]\subset \mathfrak {n}_{(i+j)A}$
in the Lie algebras
$[\mathfrak {n}_{iA},\mathfrak {n}_{jA}]\subset \mathfrak {n}_{(i+j)A}$
in the Lie algebras
![]() $\mathfrak {e}_A$
, restricting to subalgebras
$\mathfrak {e}_A$
, restricting to subalgebras ![]() , we see that we have representations
, we see that we have representations ![]() and
and ![]() given by the adjoint action of
given by the adjoint action of
![]() $\mathfrak {co}(4,4)$
or
$\mathfrak {co}(4,4)$
or
![]() $\mathfrak {co}(8,0)$
which naturally seat in
$\mathfrak {co}(8,0)$
which naturally seat in
![]() $\mathfrak {n}_{0A}$
, respectively.
$\mathfrak {n}_{0A}$
, respectively.
There is no surprise that the representations ![]() are the Dirac spinor representations (9.3) and (9.6) of the respective
are the Dirac spinor representations (9.3) and (9.6) of the respective
![]() $\mathfrak {co}(4,4)$
and
$\mathfrak {co}(4,4)$
and
![]() $\mathfrak {co}(8,0)$
parts of
$\mathfrak {co}(8,0)$
parts of
![]() $\mathfrak {n}_{0A}$
s in the 16-dimensional real vector spaces
$\mathfrak {n}_{0A}$
s in the 16-dimensional real vector spaces ![]() . As such, these representations are reducible, and they split each
. As such, these representations are reducible, and they split each
![]() $\mathfrak {n}_{0A}$
,
$\mathfrak {n}_{0A}$
,
![]() $A=I,IV$
onto two irreducible representations
$A=I,IV$
onto two irreducible representations ![]() in real 8-dimensional spaces
in real 8-dimensional spaces ![]() of Weyl spinors. This shows that the 2-step nilpotent Lie algebra
of Weyl spinors. This shows that the 2-step nilpotent Lie algebra ![]() is, for each
is, for each
![]() $A=I,IV$
, a natural representation space for the action of the three triality representations
$A=I,IV$
, a natural representation space for the action of the three triality representations
![]() $(\rho _+,\rho _-,\tau )$
. We have
$(\rho _+,\rho _-,\tau )$
. We have
and the 8-dimensional real irreducible representations
![]() $(\tau _A,\rho _A+,\rho _A-)$
of
$(\tau _A,\rho _A+,\rho _A-)$
of
![]() $\mathfrak {co}(4,4)$
or
$\mathfrak {co}(4,4)$
or
![]() $\mathfrak {co}(8,0)$
acting in the respective
$\mathfrak {co}(8,0)$
acting in the respective ![]() ,
, ![]() and
and ![]() .
.
We summarise the considerations from this section in the following theorem,
Theorem 10.1. (Natural realisation of the triality representations)
-
(1) The
 $\mathfrak {so}(4,4)$
triality: The real form
$\mathfrak {so}(4,4)$
triality: The real form
 $\mathfrak {e}_I$
of the simple exceptional Lie algebra
$\mathfrak {e}_I$
of the simple exceptional Lie algebra
 $\mathfrak {e}_6$
, when graded according to the following decoration of its Satake diagram
$\mathfrak {e}_6$
, when graded according to the following decoration of its Satake diagram  , has the
, has the  part as a real 24-dimensional vector space, naturally split onto the three real 8-dimensional components
part as a real 24-dimensional vector space, naturally split onto the three real 8-dimensional components  ,
,  and
and  ,
, 
This decomposition is
 $\mathfrak {so}(4,4)$
invariant and consists of components
$\mathfrak {so}(4,4)$
invariant and consists of components  ,
,  and
and  , on which the triality representation of
, on which the triality representation of $$ \begin{align*}\tau\oplus\rho_+\oplus\rho_-\end{align*} $$
$$ \begin{align*}\tau\oplus\rho_+\oplus\rho_-\end{align*} $$
 $\mathfrak {so}(4,4)$
acts irreducibly.
$\mathfrak {so}(4,4)$
acts irreducibly.
-
(2) The
 $\mathfrak {so}(8,0)$
triality: Likewise, the real form
$\mathfrak {so}(8,0)$
triality: Likewise, the real form
 $\mathfrak {e}_{IV}$
of the simple exceptional Lie algebra
$\mathfrak {e}_{IV}$
of the simple exceptional Lie algebra
 $\mathfrak {e}_6$
, when graded according to the following decoration of its Satake diagram
$\mathfrak {e}_6$
, when graded according to the following decoration of its Satake diagram  , has the
, has the  part as a real 24-dimensional vector space, naturally split onto the three real 8-dimensional components
part as a real 24-dimensional vector space, naturally split onto the three real 8-dimensional components  ,
,  and
and  , This decomposition is
, This decomposition is
 $\mathfrak {so}(8,0)$
invariant and consists of components
$\mathfrak {so}(8,0)$
invariant and consists of components  ,
,  and
and  , on which the triality representation of
, on which the triality representation of $$ \begin{align*}\tau\oplus\rho_+\oplus\rho_-\end{align*} $$
$$ \begin{align*}\tau\oplus\rho_+\oplus\rho_-\end{align*} $$
 $\mathfrak {so}(8,0)$
acts irreducibly.
$\mathfrak {so}(8,0)$
acts irreducibly.
10.2. An explicit realisation of
 $\mathfrak {e}_I$
in dimension 24
$\mathfrak {e}_I$
in dimension 24
Taking as
![]() $(\rho ,S)$
the Dirac spinors representation (9.3) of
$(\rho ,S)$
the Dirac spinors representation (9.3) of
![]() $\mathrm {co}(4,4)$
in dimension 16, and as
$\mathrm {co}(4,4)$
in dimension 16, and as
![]() $(\tau ,R)$
the vectorial representation (9.5) of
$(\tau ,R)$
the vectorial representation (9.5) of
![]() $\mathrm {co}(4,4)$
in dimension 8, we again are in the situation of a missing
$\mathrm {co}(4,4)$
in dimension 8, we again are in the situation of a missing
![]() $\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
from the triple
$\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
from the triple
![]() $(\rho ,\tau ,\omega )$
described by the magical equation (2.1). Solving this equation for
$(\rho ,\tau ,\omega )$
described by the magical equation (2.1). Solving this equation for
![]() $\omega $
, we obtain
$\omega $
, we obtain
![]() $\omega ^i{}_{\mu \nu }$
,
$\omega ^i{}_{\mu \nu }$
,
![]() $i=1,\dots ,8$
,
$i=1,\dots ,8$
,
![]() $\mu ,\nu =1,\dots ,16$
, which leads to the eight 2-forms
$\mu ,\nu =1,\dots ,16$
, which leads to the eight 2-forms
![]() $\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
on a 16-dimensional manifold
$\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
on a 16-dimensional manifold
![]() $N=\mathbb {R}^{16}$
, which read
$N=\mathbb {R}^{16}$
, which read
 $$ \begin{align}\begin{aligned} \omega^1=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{10}+\mathrm{d} x^2\wedge\mathrm{d} x^{9}+\mathrm{d} x^7\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{15}\\ \omega^2=\,\,&-\mathrm{d} x^2\wedge\mathrm{d} x^{12}+\mathrm{d} x^4\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{14}\\ \omega^3=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{12}+\mathrm{d} x^4\wedge\mathrm{d} x^{9}+\mathrm{d} x^5\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{13}\\ \omega^4=\,\,&-\mathrm{d} x^5\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{9}+\mathrm{d} x^7\wedge\mathrm{d} x^{12}-\mathrm{d} x^8\wedge\mathrm{d} x^{11}\\ \omega^5=\,\,&-\mathrm{d} x^2\wedge\mathrm{d} x^{11}+\mathrm{d} x^3\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{15}-\mathrm{d} x^7\wedge\mathrm{d} x^{14}\\ \omega^6=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{11}+\mathrm{d} x^3\wedge\mathrm{d} x^{9}+\mathrm{d} x^5\wedge\mathrm{d} x^{15}-\mathrm{d} x^7\wedge\mathrm{d} x^{13}\\ \omega^7=\,\,&-\mathrm{d} x^3\wedge\mathrm{d} x^{12}+\mathrm{d} x^4\wedge\mathrm{d} x^{11}+\mathrm{d} x^5\wedge\mathrm{d} x^{14}-\mathrm{d} x^6\wedge\mathrm{d} x^{13}\\ \omega^8=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{14}+\mathrm{d} x^2\wedge\mathrm{d} x^{13}+\mathrm{d} x^3\wedge\mathrm{d} x^{16}-\mathrm{d} x^4\wedge\mathrm{d} x^{15}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \omega^1=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{10}+\mathrm{d} x^2\wedge\mathrm{d} x^{9}+\mathrm{d} x^7\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{15}\\ \omega^2=\,\,&-\mathrm{d} x^2\wedge\mathrm{d} x^{12}+\mathrm{d} x^4\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{14}\\ \omega^3=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{12}+\mathrm{d} x^4\wedge\mathrm{d} x^{9}+\mathrm{d} x^5\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{13}\\ \omega^4=\,\,&-\mathrm{d} x^5\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{9}+\mathrm{d} x^7\wedge\mathrm{d} x^{12}-\mathrm{d} x^8\wedge\mathrm{d} x^{11}\\ \omega^5=\,\,&-\mathrm{d} x^2\wedge\mathrm{d} x^{11}+\mathrm{d} x^3\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{15}-\mathrm{d} x^7\wedge\mathrm{d} x^{14}\\ \omega^6=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{11}+\mathrm{d} x^3\wedge\mathrm{d} x^{9}+\mathrm{d} x^5\wedge\mathrm{d} x^{15}-\mathrm{d} x^7\wedge\mathrm{d} x^{13}\\ \omega^7=\,\,&-\mathrm{d} x^3\wedge\mathrm{d} x^{12}+\mathrm{d} x^4\wedge\mathrm{d} x^{11}+\mathrm{d} x^5\wedge\mathrm{d} x^{14}-\mathrm{d} x^6\wedge\mathrm{d} x^{13}\\ \omega^8=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{14}+\mathrm{d} x^2\wedge\mathrm{d} x^{13}+\mathrm{d} x^3\wedge\mathrm{d} x^{16}-\mathrm{d} x^4\wedge\mathrm{d} x^{15}. \end{aligned}\end{align} $$
The manifold
![]() $N=\mathbb {R}^{16}$
with these 2-forms, after contactification, gives the following Theorem.
$N=\mathbb {R}^{16}$
with these 2-forms, after contactification, gives the following Theorem.
Theorem 10.2. Let
![]() $M=\mathbb {R}^{24}$
with coordinates
$M=\mathbb {R}^{24}$
with coordinates
![]() $(u^1,\dots ,u^8,x^1,\dots ,x^{16})$
, and consider eight 1-forms
$(u^1,\dots ,u^8,x^1,\dots ,x^{16})$
, and consider eight 1-forms
![]() $\lambda ^1,\dots ,\lambda ^8$
on M given by
$\lambda ^1,\dots ,\lambda ^8$
on M given by
 $$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} u^1-x^1\mathrm{d} x^{10}+ x^2\mathrm{d} x^{9}+ x^7\mathrm{d} x^{16}- x^8\mathrm{d} x^{15}\\ \lambda^2=\,\,&\mathrm{d} u^2- x^2\mathrm{d} x^{12}+ x^4\mathrm{d} x^{10}+ x^6\mathrm{d} x^{16}- x^8\mathrm{d} x^{14}\\ \lambda^3=\,\,&\mathrm{d} u^3- x^1\mathrm{d} x^{12}+ x^4\mathrm{d} x^{9}+x^5\mathrm{d} x^{16}- x^8\mathrm{d} x^{13}\\ \lambda^4=\,\,&\mathrm{d} u^4- x^5\mathrm{d} x^{10}+ x^6\mathrm{d} x^{9}+ x^7\mathrm{d} x^{12}- x^8\mathrm{d} x^{11}\\ \lambda^5=\,\,&\mathrm{d} u^5-x^2\mathrm{d} x^{11}+ x^3\mathrm{d} x^{10}+ x^6\mathrm{d} x^{15}- x^7\mathrm{d} x^{14}\\ \lambda^6=\,\,&\mathrm{d} u^6- x^1\mathrm{d} x^{11}+ x^3\mathrm{d} x^{9}+ x^5\mathrm{d} x^{15}- x^7\mathrm{d} x^{13}\\ \lambda^7=\,\,&\mathrm{d} u^7- x^3\mathrm{d} x^{12}+ x^4\mathrm{d} x^{11}+ x^5\mathrm{d} x^{14}- x^6\mathrm{d} x^{13}\\ \lambda^8=\,\,&\mathrm{d} u^8- x^1\mathrm{d} x^{14}+ x^2\mathrm{d} x^{13}+ x^3\mathrm{d} x^{16}-x^4\mathrm{d} x^{15}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} u^1-x^1\mathrm{d} x^{10}+ x^2\mathrm{d} x^{9}+ x^7\mathrm{d} x^{16}- x^8\mathrm{d} x^{15}\\ \lambda^2=\,\,&\mathrm{d} u^2- x^2\mathrm{d} x^{12}+ x^4\mathrm{d} x^{10}+ x^6\mathrm{d} x^{16}- x^8\mathrm{d} x^{14}\\ \lambda^3=\,\,&\mathrm{d} u^3- x^1\mathrm{d} x^{12}+ x^4\mathrm{d} x^{9}+x^5\mathrm{d} x^{16}- x^8\mathrm{d} x^{13}\\ \lambda^4=\,\,&\mathrm{d} u^4- x^5\mathrm{d} x^{10}+ x^6\mathrm{d} x^{9}+ x^7\mathrm{d} x^{12}- x^8\mathrm{d} x^{11}\\ \lambda^5=\,\,&\mathrm{d} u^5-x^2\mathrm{d} x^{11}+ x^3\mathrm{d} x^{10}+ x^6\mathrm{d} x^{15}- x^7\mathrm{d} x^{14}\\ \lambda^6=\,\,&\mathrm{d} u^6- x^1\mathrm{d} x^{11}+ x^3\mathrm{d} x^{9}+ x^5\mathrm{d} x^{15}- x^7\mathrm{d} x^{13}\\ \lambda^7=\,\,&\mathrm{d} u^7- x^3\mathrm{d} x^{12}+ x^4\mathrm{d} x^{11}+ x^5\mathrm{d} x^{14}- x^6\mathrm{d} x^{13}\\ \lambda^8=\,\,&\mathrm{d} u^8- x^1\mathrm{d} x^{14}+ x^2\mathrm{d} x^{13}+ x^3\mathrm{d} x^{16}-x^4\mathrm{d} x^{15}. \end{aligned}\end{align*} $$
The rank 16 distribution
![]() ${\mathcal D}$
on M defined as
${\mathcal D}$
on M defined as ![]() has its Lie algebra of infinitesimal authomorphisms
has its Lie algebra of infinitesimal authomorphisms
![]() $\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^{16})$
is the Dirac spinors representation (9.3) of
$(\rho ,S=\mathbb {R}^{16})$
is the Dirac spinors representation (9.3) of
![]() $\mathfrak {n}_{00}=\mathfrak {co}(4,4)$
, and
$\mathfrak {n}_{00}=\mathfrak {co}(4,4)$
, and
![]() $(\tau ,R=\mathbb {R}^8)$
is the vectorial representation (9.5) of
$(\tau ,R=\mathbb {R}^8)$
is the vectorial representation (9.5) of
![]() $\mathfrak {n}_{00}$
.
$\mathfrak {n}_{00}$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
![]() $\mathfrak {e}_{I}$
,
$\mathfrak {e}_{I}$
,
having the following natural gradation
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S=S_+\oplus S_-$
,
$\mathfrak {n}_{-1}=S=S_+\oplus S_-$
,
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
, and with the spaces
$\mathfrak {n}_{2}=R^*$
, and with the spaces
![]() $S_\pm $
being the carrier spaces for the Weyl spinors representations
$S_\pm $
being the carrier spaces for the Weyl spinors representations
![]() $\rho _\pm $
of
$\rho _\pm $
of
![]() $\mathfrak {co}(4,4)$
. The gradation in
$\mathfrak {co}(4,4)$
. The gradation in
![]() $\mathfrak {e}_I$
is inherited from the distribution structure
$\mathfrak {e}_I$
is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {e}_{I}$
.
$\mathfrak {e}_{I}$
.
The contactification
![]() $(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
![]() $(E_{I},P_{I})$
related to the following crossed Satake diagram:
$(E_{I},P_{I})$
related to the following crossed Satake diagram:  .
.
Remark 10.3. Also the
![]() $\mathfrak {e}_I$
case, considered in this section, admits a description in terms of an
$\mathfrak {e}_I$
case, considered in this section, admits a description in terms of an
![]() $\mathbb {R}\oplus \mathfrak {so}(4,4)$
invariant 4-form
$\mathbb {R}\oplus \mathfrak {so}(4,4)$
invariant 4-form
![]() $\Phi $
in
$\Phi $
in
![]() $S=\mathbb {R}^{16}$
. Now
$S=\mathbb {R}^{16}$
. Now
![]() $\Phi $
may be represented by
$\Phi $
may be represented by
where
![]() $\omega ^i$
are given by (10.1) and
$\omega ^i$
are given by (10.1) and
 $$ \begin{align*}\big(\,\,h_{ij}\,\,\big)\,\,= \,\,\tfrac12\,\,\begin{pmatrix} 0&0&0&0&0&0&1&0\\0&0&0&0&0&-1&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&0&0&1\\0&0&1&0&0&0&0&0\\0&-1&0&0&0&0&0&0\\1&0&0&0&0&0&0&0\\0&0&0&1&0&0&0&0 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\big(\,\,h_{ij}\,\,\big)\,\,= \,\,\tfrac12\,\,\begin{pmatrix} 0&0&0&0&0&0&1&0\\0&0&0&0&0&-1&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&0&0&1\\0&0&1&0&0&0&0&0\\0&-1&0&0&0&0&0&0\\1&0&0&0&0&0&0&0\\0&0&0&1&0&0&0&0 \end{pmatrix}.\end{align*} $$
Explicitly, the form
![]() $\Phi $
reads
$\Phi $
reads
 $$ \begin{align}\begin{aligned} \Phi\,\,=\,\,&2\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{12}-2\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{12}+\\ &2\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{11}+2\mathrm{d} x^1\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{14}-\\&\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{14}-\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}-\\&\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}+\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}-\\ &2\mathrm{d} x^1\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{14}+2\mathrm{d} x^1\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{14}+\\&2\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{12}-2\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{11}-\\&\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{14}-\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}+\\ &\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}-\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}+\\ &2\mathrm{d} x^2\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{13}+2\mathrm{d} x^2\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{13}-\\&2\mathrm{d} x^2\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{13}+2\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{10}-\\&2\mathrm{d} x^3\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{16}+2\mathrm{d} x^3\wedge\mathrm{ d} x^6\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{16}+\\ &2\mathrm{d} x^3\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{16}-\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{14}+\\&\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}-\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}-\\&\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{15}-\\ &2\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{15}+\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{14}-\\ &\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}-\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}-\\&\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^4\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{15}+\\&2\mathrm{d} x^5\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{15}\wedge\mathrm{d} x^{16}-2\mathrm{d} x^5\wedge\mathrm{ d} x^7\wedge\mathrm{d} x^{14}\wedge\mathrm{d} x^{16}+\\ &2\mathrm{d} x^5\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{14}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^6\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{13}\wedge\mathrm{d} x^{16}-\\&2\mathrm{d} x^6\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{13}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^7\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{13}\wedge\mathrm{d} x^{14}. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \Phi\,\,=\,\,&2\mathrm{d} x^1\wedge\mathrm{d} x^2\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{12}-2\mathrm{d} x^1\wedge\mathrm{d} x^3\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{12}+\\ &2\mathrm{d} x^1\wedge\mathrm{d} x^4\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{11}+2\mathrm{d} x^1\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{14}-\\&\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{14}-\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}-\\&\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}+\mathrm{d} x^1\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}-\\ &2\mathrm{d} x^1\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{14}+2\mathrm{d} x^1\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{14}+\\&2\mathrm{d} x^2\wedge\mathrm{d} x^3\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{12}-2\mathrm{d} x^2\wedge\mathrm{d} x^4\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{11}-\\&\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^9\wedge\mathrm{d} x^{14}-\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}+\\ &\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}-\mathrm{d} x^2\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}+\\ &2\mathrm{d} x^2\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{13}+2\mathrm{d} x^2\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{13}-\\&2\mathrm{d} x^2\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{13}+2\mathrm{d} x^3\wedge\mathrm{d} x^4\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{10}-\\&2\mathrm{d} x^3\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{16}+2\mathrm{d} x^3\wedge\mathrm{ d} x^6\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{16}+\\ &2\mathrm{d} x^3\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{16}-\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{14}+\\&\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}-\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}-\\&\mathrm{d} x^3\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^4\wedge\mathrm{d} x^5\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{15}-\\ &2\mathrm{d} x^4\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{15}+\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{9}\wedge\mathrm{d} x^{14}-\\ &\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{10}\wedge\mathrm{d} x^{13}-\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{16}-\\&\mathrm{d} x^4\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{12}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^4\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{11}\wedge\mathrm{d} x^{15}+\\&2\mathrm{d} x^5\wedge\mathrm{d} x^6\wedge\mathrm{d} x^{15}\wedge\mathrm{d} x^{16}-2\mathrm{d} x^5\wedge\mathrm{ d} x^7\wedge\mathrm{d} x^{14}\wedge\mathrm{d} x^{16}+\\ &2\mathrm{d} x^5\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{14}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^6\wedge\mathrm{d} x^7\wedge\mathrm{d} x^{13}\wedge\mathrm{d} x^{16}-\\&2\mathrm{d} x^6\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{13}\wedge\mathrm{d} x^{15}+2\mathrm{d} x^7\wedge\mathrm{d} x^8\wedge\mathrm{d} x^{13}\wedge\mathrm{d} x^{14}. \end{aligned} \end{align} $$
This 4-form is such that its stabiliser in
![]() $\mathfrak {gl}(16,\mathbb {R})$
is
$\mathfrak {gl}(16,\mathbb {R})$
is
![]() $\mathfrak {n}_0=\mathbb {R}\oplus \mathfrak {co}(4,4)$
. When restricted to
$\mathfrak {n}_0=\mathbb {R}\oplus \mathfrak {co}(4,4)$
. When restricted to
![]() $\mathfrak {n}_{00}=\mathfrak {co}(4,4)$
this stabiliser is given precisely in the Mayorana Dirac spinor representation
$\mathfrak {n}_{00}=\mathfrak {co}(4,4)$
this stabiliser is given precisely in the Mayorana Dirac spinor representation
10.3. An explicit realisation of
 $\mathfrak {e}_{IV}$
in dimension 24
$\mathfrak {e}_{IV}$
in dimension 24
Similarly, as in the previous section, we take as
![]() $(\rho ,S)$
the Dirac spinors representation (9.6) of
$(\rho ,S)$
the Dirac spinors representation (9.6) of
![]() $\mathrm {co}(8.0)$
in dimension 16, and as
$\mathrm {co}(8.0)$
in dimension 16, and as
![]() $(\tau ,R)$
the vectorial representation (9.8) of
$(\tau ,R)$
the vectorial representation (9.8) of
![]() $\mathrm {co}(8,0)$
in dimension 8, and we search for
$\mathrm {co}(8,0)$
in dimension 8, and we search for
![]() $\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
, solving the magical equation (2.1). We obtain
$\omega \in \mathrm {Hom}(\bigwedge ^2S,R)$
, solving the magical equation (2.1). We obtain
![]() $\omega ^i{}_{\mu \nu }$
,
$\omega ^i{}_{\mu \nu }$
,
![]() $i=1,\dots ,8$
,
$i=1,\dots ,8$
,
![]() $\mu ,\nu =1,\dots ,16$
, which provides us with the eight 2-forms
$\mu ,\nu =1,\dots ,16$
, which provides us with the eight 2-forms
![]() $\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
on a 16-dimensional manifold
$\omega ^i=\tfrac 12\omega ^i{}_{\mu \nu }\mathrm {d} x^\mu \wedge \mathrm {d} x^\nu $
on a 16-dimensional manifold
![]() $N=\mathbb {R}^{16}$
, which read
$N=\mathbb {R}^{16}$
, which read
 $$ \begin{align}\begin{aligned} \omega^1=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{9}+\mathrm{d} x^2\wedge\mathrm{d} x^{10}+\mathrm{d} x^3\wedge\mathrm{d} x^{11}+\mathrm{d} x^4\wedge\mathrm{d} x^{12}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{13}-\mathrm{d} x^6\wedge\mathrm{d} x^{14}-\mathrm{d} x^7\wedge\mathrm{d} x^{15}-\mathrm{d} x^8\wedge\mathrm{d} x^{16}\\ \omega^2=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{10}+\mathrm{d} x^2\wedge\mathrm{d} x^{9}+\mathrm{d} x^3\wedge\mathrm{d} x^{12}-\mathrm{d} x^4\wedge\mathrm{d} x^{11}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{14}+\mathrm{d} x^6\wedge\mathrm{d} x^{13}+\mathrm{d} x^7\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{15}\\ \omega^3=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{11}-\mathrm{d} x^2\wedge\mathrm{d} x^{12}+\mathrm{d} x^3\wedge\mathrm{d} x^{9}+\mathrm{d} x^4\wedge\mathrm{d} x^{10}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{15}+\mathrm{d} x^6\wedge\mathrm{d} x^{16}-\mathrm{d} x^7\wedge\mathrm{d} x^{13}-\mathrm{d} x^8\wedge\mathrm{d} x^{14}\\ \omega^4=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{12}+\mathrm{d} x^2\wedge\mathrm{d} x^{11}-\mathrm{d} x^3\wedge\mathrm{d} x^{10}+\mathrm{d} x^4\wedge\mathrm{d} x^{9}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{16}-\mathrm{d} x^6\wedge\mathrm{d} x^{15}+\mathrm{d} x^7\wedge\mathrm{d} x^{14}-\mathrm{d} x^8\wedge\mathrm{d} x^{13}\\ \omega^5=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{13}+\mathrm{d} x^2\wedge\mathrm{d} x^{14}-\mathrm{d} x^3\wedge\mathrm{d} x^{15}-\mathrm{d} x^4\wedge\mathrm{d} x^{16}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{9}+\mathrm{d} x^6\wedge\mathrm{d} x^{10}-\mathrm{d} x^7\wedge\mathrm{d} x^{11}-\mathrm{d} x^8\wedge\mathrm{d} x^{12}\\ \omega^6=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{14}-\mathrm{d} x^2\wedge\mathrm{d} x^{13}-\mathrm{d} x^3\wedge\mathrm{d} x^{16}+\mathrm{d} x^4\wedge\mathrm{d} x^{15}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{9}+\mathrm{d} x^7\wedge\mathrm{d} x^{12}-\mathrm{d} x^8\wedge\mathrm{d} x^{11}\\ \omega^7=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{15}-\mathrm{d} x^2\wedge\mathrm{d} x^{16}+\mathrm{d} x^3\wedge\mathrm{d} x^{13}-\mathrm{d} x^4\wedge\mathrm{d} x^{14}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{11}-\mathrm{d} x^6\wedge\mathrm{d} x^{12}+\mathrm{d} x^7\wedge\mathrm{d} x^{9}-\mathrm{d} x^8\wedge\mathrm{d} x^{10}\\ \omega^8=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{16}-\mathrm{d} x^2\wedge\mathrm{d} x^{15}-\mathrm{d} x^3\wedge\mathrm{d} x^{14}-\mathrm{d} x^4\wedge\mathrm{d} x^{13}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{12}-\mathrm{d} x^6\wedge\mathrm{d} x^{11}-\mathrm{d} x^7\wedge\mathrm{d} x^{10}-\mathrm{d} x^8\wedge\mathrm{d} x^{9}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \omega^1=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{9}+\mathrm{d} x^2\wedge\mathrm{d} x^{10}+\mathrm{d} x^3\wedge\mathrm{d} x^{11}+\mathrm{d} x^4\wedge\mathrm{d} x^{12}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{13}-\mathrm{d} x^6\wedge\mathrm{d} x^{14}-\mathrm{d} x^7\wedge\mathrm{d} x^{15}-\mathrm{d} x^8\wedge\mathrm{d} x^{16}\\ \omega^2=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{10}+\mathrm{d} x^2\wedge\mathrm{d} x^{9}+\mathrm{d} x^3\wedge\mathrm{d} x^{12}-\mathrm{d} x^4\wedge\mathrm{d} x^{11}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{14}+\mathrm{d} x^6\wedge\mathrm{d} x^{13}+\mathrm{d} x^7\wedge\mathrm{d} x^{16}-\mathrm{d} x^8\wedge\mathrm{d} x^{15}\\ \omega^3=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{11}-\mathrm{d} x^2\wedge\mathrm{d} x^{12}+\mathrm{d} x^3\wedge\mathrm{d} x^{9}+\mathrm{d} x^4\wedge\mathrm{d} x^{10}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{15}+\mathrm{d} x^6\wedge\mathrm{d} x^{16}-\mathrm{d} x^7\wedge\mathrm{d} x^{13}-\mathrm{d} x^8\wedge\mathrm{d} x^{14}\\ \omega^4=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{12}+\mathrm{d} x^2\wedge\mathrm{d} x^{11}-\mathrm{d} x^3\wedge\mathrm{d} x^{10}+\mathrm{d} x^4\wedge\mathrm{d} x^{9}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{16}-\mathrm{d} x^6\wedge\mathrm{d} x^{15}+\mathrm{d} x^7\wedge\mathrm{d} x^{14}-\mathrm{d} x^8\wedge\mathrm{d} x^{13}\\ \omega^5=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{13}+\mathrm{d} x^2\wedge\mathrm{d} x^{14}-\mathrm{d} x^3\wedge\mathrm{d} x^{15}-\mathrm{d} x^4\wedge\mathrm{d} x^{16}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{9}+\mathrm{d} x^6\wedge\mathrm{d} x^{10}-\mathrm{d} x^7\wedge\mathrm{d} x^{11}-\mathrm{d} x^8\wedge\mathrm{d} x^{12}\\ \omega^6=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{14}-\mathrm{d} x^2\wedge\mathrm{d} x^{13}-\mathrm{d} x^3\wedge\mathrm{d} x^{16}+\mathrm{d} x^4\wedge\mathrm{d} x^{15}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{10}+\mathrm{d} x^6\wedge\mathrm{d} x^{9}+\mathrm{d} x^7\wedge\mathrm{d} x^{12}-\mathrm{d} x^8\wedge\mathrm{d} x^{11}\\ \omega^7=\,\,&\mathrm{d} x^1\wedge\mathrm{d} x^{15}-\mathrm{d} x^2\wedge\mathrm{d} x^{16}+\mathrm{d} x^3\wedge\mathrm{d} x^{13}-\mathrm{d} x^4\wedge\mathrm{d} x^{14}+\\&\mathrm{d} x^5\wedge\mathrm{d} x^{11}-\mathrm{d} x^6\wedge\mathrm{d} x^{12}+\mathrm{d} x^7\wedge\mathrm{d} x^{9}-\mathrm{d} x^8\wedge\mathrm{d} x^{10}\\ \omega^8=\,\,&-\mathrm{d} x^1\wedge\mathrm{d} x^{16}-\mathrm{d} x^2\wedge\mathrm{d} x^{15}-\mathrm{d} x^3\wedge\mathrm{d} x^{14}-\mathrm{d} x^4\wedge\mathrm{d} x^{13}-\\&\mathrm{d} x^5\wedge\mathrm{d} x^{12}-\mathrm{d} x^6\wedge\mathrm{d} x^{11}-\mathrm{d} x^7\wedge\mathrm{d} x^{10}-\mathrm{d} x^8\wedge\mathrm{d} x^{9}. \end{aligned}\end{align} $$
Contactifying, we have the following theorem:
Theorem 10.4. Let
![]() $M=\mathbb {R}^{24}$
with coordinates
$M=\mathbb {R}^{24}$
with coordinates
![]() $(u^1,\dots ,u^8,x^1,\dots ,x^{16})$
, and consider eight 1-forms
$(u^1,\dots ,u^8,x^1,\dots ,x^{16})$
, and consider eight 1-forms
![]() $\lambda ^1,\dots ,\lambda ^8$
on M given by
$\lambda ^1,\dots ,\lambda ^8$
on M given by
 $$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} u^1+ x^1\mathrm{d} x^{9}+ x^2\mathrm{d} x^{10}+ x^3 \mathrm{d} x^{11}+ x^4 \mathrm{d} x^{12}- x^5 \mathrm{d} x^{13}- x^6 \mathrm{d} x^{14}- x^7 \mathrm{d} x^{15}- x^8 \mathrm{d} x^{16}\\ \lambda^2=\,\,&\mathrm{d} u^2- x^1 \mathrm{d} x^{10}+ x^2 \mathrm{d} x^{9}+ x^3 \mathrm{d} x^{12}- x^4 \mathrm{d} x^{11}- x^5 \mathrm{d} x^{14}+ x^6 \mathrm{d} x^{13}+ x^7 \mathrm{d} x^{16}- x^8 \mathrm{d} x^{15}\\ \lambda^3=\,\,&\mathrm{d} u^3- x^1 \mathrm{d} x^{11}- x^2 \mathrm{d} x^{12}+ x^3 \mathrm{d} x^{9}+ x^4 \mathrm{d} x^{10}+ x^5 \mathrm{d} x^{15}+ x^6 \mathrm{d} x^{16}- x^7 \mathrm{d} x^{13}- x^8 \mathrm{d} x^{14}\\ \lambda^4=\,\,&\mathrm{d} u^4- x^1 \mathrm{d} x^{12}+ x^2 \mathrm{d} x^{11}- x^3 \mathrm{d} x^{10}+ x^4 \mathrm{d} x^{9}+ x^5 \mathrm{d} x^{16}- x^6 \mathrm{d} x^{15}+ x^7 \mathrm{d} x^{14}- x^8 \mathrm{d} x^{13}\\ \lambda^5=\,\,&\mathrm{d} u^5+ x^1 \mathrm{d} x^{13}+ x^2 \mathrm{d} x^{14}- x^3 \mathrm{d} x^{15}- x^4 \mathrm{d} x^{16}+ x^5 \mathrm{d} x^{9}+ x^6 \mathrm{d} x^{10}- x^7 \mathrm{d} x^{11}- x^8 \mathrm{d} x^{12}\\ \lambda^6=\,\,&\mathrm{d} u^6+ x^1 \mathrm{d} x^{14}- x^2 \mathrm{d} x^{13}- x^3 \mathrm{d} x^{16}+ x^4 \mathrm{d} x^{15}- x^5 \mathrm{d} x^{10}+ x^6 \mathrm{d} x^{9}+ x^7 \mathrm{d} x^{12}- x^8 \mathrm{d} x^{11}\\ \lambda^7=\,\,&\mathrm{d} u^7+ x^1 \mathrm{d} x^{15}- x^2 \mathrm{d} x^{16}+ x^3 \mathrm{d} x^{13}- x^4 \mathrm{d} x^{14}+ x^5 \mathrm{d} x^{11}- x^6 \mathrm{d} x^{12}+ x^7 \mathrm{d} x^{9}- x^8 \mathrm{d} x^{10}\\ \lambda^8=\,\,&\mathrm{d} u^8 - x^1 \mathrm{d} x^{16}- x^2 \mathrm{d} x^{15}- x^3 \mathrm{d} x^{14}- x^4 \mathrm{d} x^{13}- x^5 \mathrm{d} x^{12}- x^6 \mathrm{d} x^{11}- x^7 \mathrm{d} x^{10}- x^8 \mathrm{d} x^{9}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} u^1+ x^1\mathrm{d} x^{9}+ x^2\mathrm{d} x^{10}+ x^3 \mathrm{d} x^{11}+ x^4 \mathrm{d} x^{12}- x^5 \mathrm{d} x^{13}- x^6 \mathrm{d} x^{14}- x^7 \mathrm{d} x^{15}- x^8 \mathrm{d} x^{16}\\ \lambda^2=\,\,&\mathrm{d} u^2- x^1 \mathrm{d} x^{10}+ x^2 \mathrm{d} x^{9}+ x^3 \mathrm{d} x^{12}- x^4 \mathrm{d} x^{11}- x^5 \mathrm{d} x^{14}+ x^6 \mathrm{d} x^{13}+ x^7 \mathrm{d} x^{16}- x^8 \mathrm{d} x^{15}\\ \lambda^3=\,\,&\mathrm{d} u^3- x^1 \mathrm{d} x^{11}- x^2 \mathrm{d} x^{12}+ x^3 \mathrm{d} x^{9}+ x^4 \mathrm{d} x^{10}+ x^5 \mathrm{d} x^{15}+ x^6 \mathrm{d} x^{16}- x^7 \mathrm{d} x^{13}- x^8 \mathrm{d} x^{14}\\ \lambda^4=\,\,&\mathrm{d} u^4- x^1 \mathrm{d} x^{12}+ x^2 \mathrm{d} x^{11}- x^3 \mathrm{d} x^{10}+ x^4 \mathrm{d} x^{9}+ x^5 \mathrm{d} x^{16}- x^6 \mathrm{d} x^{15}+ x^7 \mathrm{d} x^{14}- x^8 \mathrm{d} x^{13}\\ \lambda^5=\,\,&\mathrm{d} u^5+ x^1 \mathrm{d} x^{13}+ x^2 \mathrm{d} x^{14}- x^3 \mathrm{d} x^{15}- x^4 \mathrm{d} x^{16}+ x^5 \mathrm{d} x^{9}+ x^6 \mathrm{d} x^{10}- x^7 \mathrm{d} x^{11}- x^8 \mathrm{d} x^{12}\\ \lambda^6=\,\,&\mathrm{d} u^6+ x^1 \mathrm{d} x^{14}- x^2 \mathrm{d} x^{13}- x^3 \mathrm{d} x^{16}+ x^4 \mathrm{d} x^{15}- x^5 \mathrm{d} x^{10}+ x^6 \mathrm{d} x^{9}+ x^7 \mathrm{d} x^{12}- x^8 \mathrm{d} x^{11}\\ \lambda^7=\,\,&\mathrm{d} u^7+ x^1 \mathrm{d} x^{15}- x^2 \mathrm{d} x^{16}+ x^3 \mathrm{d} x^{13}- x^4 \mathrm{d} x^{14}+ x^5 \mathrm{d} x^{11}- x^6 \mathrm{d} x^{12}+ x^7 \mathrm{d} x^{9}- x^8 \mathrm{d} x^{10}\\ \lambda^8=\,\,&\mathrm{d} u^8 - x^1 \mathrm{d} x^{16}- x^2 \mathrm{d} x^{15}- x^3 \mathrm{d} x^{14}- x^4 \mathrm{d} x^{13}- x^5 \mathrm{d} x^{12}- x^6 \mathrm{d} x^{11}- x^7 \mathrm{d} x^{10}- x^8 \mathrm{d} x^{9}. \end{aligned}\end{align*} $$
The rank 16 distribution
![]() ${\mathcal D}$
on M defined as
${\mathcal D}$
on M defined as ![]() has its Lie algebra of infinitesimal authomorphisms
has its Lie algebra of infinitesimal authomorphisms
![]() $\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^{16})$
is the Dirac spinors representation (9.3) of
$(\rho ,S=\mathbb {R}^{16})$
is the Dirac spinors representation (9.3) of
![]() $\mathfrak {n}_{00}=\mathfrak {co}(8,0)$
, and
$\mathfrak {n}_{00}=\mathfrak {co}(8,0)$
, and
![]() $(\tau ,R=\mathbb {R}^8)$
is the vectorial representation (9.5) of
$(\tau ,R=\mathbb {R}^8)$
is the vectorial representation (9.5) of
![]() $\mathfrak {n}_{00}$
.
$\mathfrak {n}_{00}$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
![]() $\mathfrak {e}_{IV}$
,
$\mathfrak {e}_{IV}$
,
having the following natural gradation:
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S=S_+\oplus S_-$
,
$\mathfrak {n}_{-1}=S=S_+\oplus S_-$
,
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
, and with the spaces
$\mathfrak {n}_{2}=R^*$
, and with the spaces
![]() $S_\pm $
being the Carrier spaces for the Weyl spinors representations
$S_\pm $
being the Carrier spaces for the Weyl spinors representations
![]() $\rho _\pm $
of
$\rho _\pm $
of
![]() $\mathfrak {co}(8,0)$
. The gradation in
$\mathfrak {co}(8,0)$
. The gradation in
![]() $e_{iV}$
is inherited from the distribution structure
$e_{iV}$
is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {e}_{IV}$
.
$\mathfrak {e}_{IV}$
.
The contactification
![]() $(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
![]() $(E_{IV},P_{IV})$
related to the following crossed Satake diagram:
$(E_{IV},P_{IV})$
related to the following crossed Satake diagram:  .
.
Remark 10.5. Again, we have a description of the relevant representations in terms of an
![]() $\mathbb {R}\oplus \mathfrak {co}(8,0)$
invariant 4-form
$\mathbb {R}\oplus \mathfrak {co}(8,0)$
invariant 4-form
![]() $\Phi $
in
$\Phi $
in
![]() $S=\mathbb {R}^{16}$
. Now
$S=\mathbb {R}^{16}$
. Now
![]() $\Phi $
may be represented by
$\Phi $
may be represented by
where
![]() $\omega ^i$
are given by (10.3) and
$\omega ^i$
are given by (10.3) and
 $$ \begin{align*}\big(\,\,h_{ij}\,\,\big)\,\,=\,\, \begin{pmatrix} 1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*}\big(\,\,h_{ij}\,\,\big)\,\,=\,\, \begin{pmatrix} 1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&1 \end{pmatrix}. \end{align*} $$
This 4-form is such that its stabiliser in
![]() $\mathfrak {gl}(16,\mathbb {R})$
is
$\mathfrak {gl}(16,\mathbb {R})$
is
![]() $\mathfrak {n}_0=\mathbb {R}\oplus \mathfrak {co}(8,0)$
. When restricted to
$\mathfrak {n}_0=\mathbb {R}\oplus \mathfrak {co}(8,0)$
. When restricted to
![]() $\mathfrak {n}_{00}=\mathfrak {co}(8,0)$
, this stabiliser is given precisely in the Mayorana Dirac spinor representation
$\mathfrak {n}_{00}=\mathfrak {co}(8,0)$
, this stabiliser is given precisely in the Mayorana Dirac spinor representation
11. Application: one more realisation of
 $\mathfrak {e}_6$
and a realisation of
$\mathfrak {e}_6$
and a realisation of
 $\mathfrak {b}_6$
$\mathfrak {b}_6$
Between the 24-dimensional realisations of
![]() $\mathfrak {e}_6$
mentioned in this paper, and Cartan’s 16-dimensional realisation of
$\mathfrak {e}_6$
mentioned in this paper, and Cartan’s 16-dimensional realisation of
![]() $\mathfrak {e}_6$
associated with the grading
$\mathfrak {e}_6$
associated with the grading  , there are 21-dimensional realisations of this algebra
, there are 21-dimensional realisations of this algebra
![]() $\mathfrak {e}_6$
associated with the following Dynkin diagram crossing:
$\mathfrak {e}_6$
associated with the following Dynkin diagram crossing:  . These define contact
. These define contact
![]() $\mathfrak {e}_6$
geometries and are described in [Reference Čap and Slovák11] p. 425–426.
$\mathfrak {e}_6$
geometries and are described in [Reference Čap and Slovák11] p. 425–426.
11.1. Realisation of
 $\mathfrak {e}_I$
in dimension 25
$\mathfrak {e}_I$
in dimension 25
Here, we will briefly discuss yet another realisation, now in dimension 25, corresponding to the following Dynkin diagram crossing:  of
of
![]() $\mathfrak {e}_6$
. This is, for example, mentioned in [Reference Kraśkiewicz and Weyman15]. Looking at the Satake diagrams of real forms of
$\mathfrak {e}_6$
. This is, for example, mentioned in [Reference Kraśkiewicz and Weyman15]. Looking at the Satake diagrams of real forms of
![]() $\mathfrak {e}_6$
, we see that this realisation is only possible for the real form
$\mathfrak {e}_6$
, we see that this realisation is only possible for the real form
![]() $\mathfrak {e}_I$
.
$\mathfrak {e}_I$
.
So we again use our Corollary 4.1 with now
![]() $\mathfrak {n}_{00}=\mathfrak {sl}(2,\mathbb {R})\oplus \mathfrak {sl}(5,\mathbb {R})$
and with representations
$\mathfrak {n}_{00}=\mathfrak {sl}(2,\mathbb {R})\oplus \mathfrak {sl}(5,\mathbb {R})$
and with representations
![]() $(\rho ,S)$
and
$(\rho ,S)$
and
![]() $(\tau ,R)$
, as indicated in [Reference Kraśkiewicz and Weyman15] Section 5.3,
$(\tau ,R)$
, as indicated in [Reference Kraśkiewicz and Weyman15] Section 5.3,
![]() $S=\mathbb {R}^2\otimes \bigwedge ^2\mathbb {R}^5,\quad R=\bigwedge ^2\mathbb {R}^2\otimes \bigwedge ^4\mathbb {R}^5.$
$S=\mathbb {R}^2\otimes \bigwedge ^2\mathbb {R}^5,\quad R=\bigwedge ^2\mathbb {R}^2\otimes \bigwedge ^4\mathbb {R}^5.$
To be more explicit, we obtain this representations as follows:
-
• We start with the defining representations
 $\tau _2$
of
$\tau _2$
of
 $\mathfrak {sl}(2,\mathbb {R})$
in
$\mathfrak {sl}(2,\mathbb {R})$
in
 $\mathbb {R}^2$
and
$\mathbb {R}^2$
and
 $\tau _5$
of
$\tau _5$
of
 $\mathfrak {sl}(5,\mathbb {R})$
in
$\mathfrak {sl}(5,\mathbb {R})$
in
 $\mathbb {R}^5$
, and we define the representation The representation
$\mathbb {R}^5$
, and we define the representation The representation $$ \begin{align*}\rho=\tau_2\otimes\big(\tau_5\wedge\tau_5\big)\quad\mathrm{of}\quad \mathfrak{sl}(2,\mathbb{R})\oplus\mathfrak{sl}(5,\mathbb{R})\quad\mathrm{ in}\quad \textstyle S=\mathbb{R}^2\otimes\bigwedge^2\mathbb{R}^5=\mathbb{R}^{20}.\end{align*} $$
$$ \begin{align*}\rho=\tau_2\otimes\big(\tau_5\wedge\tau_5\big)\quad\mathrm{of}\quad \mathfrak{sl}(2,\mathbb{R})\oplus\mathfrak{sl}(5,\mathbb{R})\quad\mathrm{ in}\quad \textstyle S=\mathbb{R}^2\otimes\bigwedge^2\mathbb{R}^5=\mathbb{R}^{20}.\end{align*} $$
 $(\rho ,S)$
is an irreducible real 20-dimensional representation of
$(\rho ,S)$
is an irreducible real 20-dimensional representation of  $$ \begin{align*}\mathfrak{n}_{00}=\mathfrak{sl}(2,\mathbb{R})\oplus\mathfrak{sl}(5,\mathbb{R}).\end{align*} $$
$$ \begin{align*}\mathfrak{n}_{00}=\mathfrak{sl}(2,\mathbb{R})\oplus\mathfrak{sl}(5,\mathbb{R}).\end{align*} $$
-
• Then we decompose the
 $190$
-dimensional representation
$190$
-dimensional representation
 $\rho \wedge \rho $
onto the irreducibles: with
$\rho \wedge \rho $
onto the irreducibles: with $$ \begin{align*}\textstyle \rho\wedge\rho=\alpha\oplus\tau\oplus\beta\quad\mathrm{in}\quad\bigwedge_{50}\oplus R\oplus\bigwedge_{135},\end{align*} $$
$$ \begin{align*}\textstyle \rho\wedge\rho=\alpha\oplus\tau\oplus\beta\quad\mathrm{in}\quad\bigwedge_{50}\oplus R\oplus\bigwedge_{135},\end{align*} $$
 $(\alpha ,\bigwedge _{50})$
being 50-dimensional,
$(\alpha ,\bigwedge _{50})$
being 50-dimensional,
 $(\tau ,R)$
being 5-dimensional and
$(\tau ,R)$
being 5-dimensional and
 $(\beta ,\bigwedge _{135})$
being
$(\beta ,\bigwedge _{135})$
being
 $135$
-dimensional.
$135$
-dimensional.
-
• We take the 20-dimensional representation
 $(\rho ,S)$
and the
$(\rho ,S)$
and the
 $5$
-dimensional representation
$5$
-dimensional representation
 $(\tau ,R)$
of
$(\tau ,R)$
of
 $\mathfrak {n}_{00}=\mathfrak {sl}(2,\mathbb {R})\oplus \mathfrak {sl}(5,\mathbb {R})$
as above, and we apply our Corollary 4.1.
$\mathfrak {n}_{00}=\mathfrak {sl}(2,\mathbb {R})\oplus \mathfrak {sl}(5,\mathbb {R})$
as above, and we apply our Corollary 4.1.
We obtain the following theorem.
Theorem 11.1. Let
![]() $M=\mathbb {R}^{25}$
with coordinates
$M=\mathbb {R}^{25}$
with coordinates
![]() $(u^1,\dots ,u^5,x^1,\dots ,x^{20})$
, and consider five 1-forms
$(u^1,\dots ,u^5,x^1,\dots ,x^{20})$
, and consider five 1-forms
![]() $\lambda ^1,\dots ,\lambda ^5$
on M given by
$\lambda ^1,\dots ,\lambda ^5$
on M given by
 $$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} u^1- x^3\mathrm{d} x^{20}+ x^5\mathrm{d} x^{19}- x^6 \mathrm{d} x^{18}- x^8 \mathrm{d} x^{16}+ x^9 \mathrm{d} x^{15}- x^{10} \mathrm{d} x^{13}\\ \lambda^2=\,\,&\mathrm{d} u^2- x^2 \mathrm{d} x^{20}+ x^4 \mathrm{d} x^{19}- x^6 \mathrm{d} x^{17}- x^7 \mathrm{d} x^{16}+ x^9 \mathrm{d} x^{14}- x^{10} \mathrm{d} x^{12}\\ \lambda^3=\,\,&\mathrm{d} u^3- x^1 \mathrm{d} x^{20}+ x^4 \mathrm{d} x^{18}-x^5 \mathrm{d} x^{17}- x^7 \mathrm{d} x^{15}+ x^8 \mathrm{d} x^{14}- x^{10} \mathrm{d} x^{11}\\ \lambda^4=\,\,&\mathrm{d} u^4- x^1 \mathrm{d} x^{19}+ x^2 \mathrm{d} x^{18}- x^3 \mathrm{d} x^{17}- x^7 \mathrm{d} x^{13}+ x^8 \mathrm{d} x^{12}- x^9 \mathrm{d} x^{11}\\ \lambda^5=\,\,&\mathrm{d} u^5- x^1 \mathrm{d} x^{16}+ x^2 \mathrm{d} x^{15}- x^3 \mathrm{d} x^{14}- x^4 \mathrm{d} x^{13}+ x^5 \mathrm{d} x^{12}- x^6 \mathrm{d} x^{11}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \lambda^1=\,\,&\mathrm{d} u^1- x^3\mathrm{d} x^{20}+ x^5\mathrm{d} x^{19}- x^6 \mathrm{d} x^{18}- x^8 \mathrm{d} x^{16}+ x^9 \mathrm{d} x^{15}- x^{10} \mathrm{d} x^{13}\\ \lambda^2=\,\,&\mathrm{d} u^2- x^2 \mathrm{d} x^{20}+ x^4 \mathrm{d} x^{19}- x^6 \mathrm{d} x^{17}- x^7 \mathrm{d} x^{16}+ x^9 \mathrm{d} x^{14}- x^{10} \mathrm{d} x^{12}\\ \lambda^3=\,\,&\mathrm{d} u^3- x^1 \mathrm{d} x^{20}+ x^4 \mathrm{d} x^{18}-x^5 \mathrm{d} x^{17}- x^7 \mathrm{d} x^{15}+ x^8 \mathrm{d} x^{14}- x^{10} \mathrm{d} x^{11}\\ \lambda^4=\,\,&\mathrm{d} u^4- x^1 \mathrm{d} x^{19}+ x^2 \mathrm{d} x^{18}- x^3 \mathrm{d} x^{17}- x^7 \mathrm{d} x^{13}+ x^8 \mathrm{d} x^{12}- x^9 \mathrm{d} x^{11}\\ \lambda^5=\,\,&\mathrm{d} u^5- x^1 \mathrm{d} x^{16}+ x^2 \mathrm{d} x^{15}- x^3 \mathrm{d} x^{14}- x^4 \mathrm{d} x^{13}+ x^5 \mathrm{d} x^{12}- x^6 \mathrm{d} x^{11}. \end{aligned}\end{align*} $$
The rank 20 distribution
![]() ${\mathcal D}$
on M defined as
${\mathcal D}$
on M defined as ![]() has its Lie algebra of infinitesimal authomorphisms
has its Lie algebra of infinitesimal authomorphisms
![]() $\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^{20})$
is the 20-dimensional irreducible representation of
$(\rho ,S=\mathbb {R}^{20})$
is the 20-dimensional irreducible representation of
![]() $\mathfrak {n}_{00}=\mathfrak {sl}(2,\mathbb {R})\oplus \mathfrak {sl}(5,\mathbb {R})$
, and
$\mathfrak {n}_{00}=\mathfrak {sl}(2,\mathbb {R})\oplus \mathfrak {sl}(5,\mathbb {R})$
, and
![]() $(\tau ,R=\mathbb {R}^5)$
is the 5-dimensional irreducible subrepresentation
$(\tau ,R=\mathbb {R}^5)$
is the 5-dimensional irreducible subrepresentation
![]() $\tau \in (\rho \wedge \rho )$
of
$\tau \in (\rho \wedge \rho )$
of
![]() $\mathfrak {n}_{00}$
.
$\mathfrak {n}_{00}$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
![]() $\mathfrak {e}_{I}$
,
$\mathfrak {e}_{I}$
,
having the following natural gradation:
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S$
,
$\mathfrak {n}_{-1}=S$
,
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
. The gradation in
$\mathfrak {n}_{2}=R^*$
. The gradation in
![]() $e_I$
is inherited from the distribution structure
$e_I$
is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {e}_{I}$
.
$\mathfrak {e}_{I}$
.
The contactification
![]() $(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
![]() $(E_{I},P_{I*})$
related to the following crossed Satake diagram:
$(E_{I},P_{I*})$
related to the following crossed Satake diagram:  .
.
11.2. A realisation of
 $\mathfrak {so}(7,6)$
in dimension 21
$\mathfrak {so}(7,6)$
in dimension 21
We know from[Reference Čap and Slovák11] that the crossed Satake diagram  corresponds to the
corresponds to the
![]() $\mathfrak {e}_I$
-symmetric contact geometry in dimension 21. It corresponds to the grading
$\mathfrak {e}_I$
-symmetric contact geometry in dimension 21. It corresponds to the grading
with
![]() $\dim (\mathfrak {n}_{\pm 1})=20$
,
$\dim (\mathfrak {n}_{\pm 1})=20$
,
![]() $\dim (\mathfrak {n}_{\pm 2})=1$
and
$\dim (\mathfrak {n}_{\pm 2})=1$
and
![]() $\mathfrak {n}_0=\mathfrak {gl}(6,\mathbb {R})$
.
$\mathfrak {n}_0=\mathfrak {gl}(6,\mathbb {R})$
.
Interestingly, dimension
![]() $n=78$
is the dimension not only of the exceptional simple Lie algebra
$n=78$
is the dimension not only of the exceptional simple Lie algebra
![]() $\mathfrak {e}_6$
, but also for the simple Lie algebras
$\mathfrak {e}_6$
, but also for the simple Lie algebras
![]() $\mathfrak {b}_6$
and
$\mathfrak {b}_6$
and
![]() $\mathfrak {c}_6$
. For example, if we take the crossed Satake diagram
$\mathfrak {c}_6$
. For example, if we take the crossed Satake diagram ![]() , we describe the following gradation
, we describe the following gradation
with
![]() $\dim (\mathfrak {n}_{\pm 1})=6$
,
$\dim (\mathfrak {n}_{\pm 1})=6$
,
![]() $\dim (\mathfrak {n}_{\pm 2})=15$
and
$\dim (\mathfrak {n}_{\pm 2})=15$
and
![]() $\mathfrak {n}_0=\mathfrak {gl}(6,\mathbb {R})$
, in the simple Lie algebra
$\mathfrak {n}_0=\mathfrak {gl}(6,\mathbb {R})$
, in the simple Lie algebra
![]() $\mathfrak {so}(7,6)$
. Here, taking
$\mathfrak {so}(7,6)$
. Here, taking
![]() $(\rho ,S)$
as the defining representation
$(\rho ,S)$
as the defining representation
![]() $\rho (A)=A$
of
$\rho (A)=A$
of
![]() $\mathbf {GL}(6,\mathbb {R})$
in
$\mathbf {GL}(6,\mathbb {R})$
in
![]() $S=\mathbb {R}^6$
, taking the representation
$S=\mathbb {R}^6$
, taking the representation
![]() $(\tau ,R)$
to be
$(\tau ,R)$
to be
![]() $\tau =\rho \wedge \rho $
in
$\tau =\rho \wedge \rho $
in
![]() $R=\bigwedge ^2\mathbb {R}^6=\mathbb {R}^{15}$
, and applying our Corollary 4.1, we get the following theorem.Footnote
7
$R=\bigwedge ^2\mathbb {R}^6=\mathbb {R}^{15}$
, and applying our Corollary 4.1, we get the following theorem.Footnote
7
Theorem 11.2. Let
![]() $M=\mathbb {R}^{21}$
with coordinates
$M=\mathbb {R}^{21}$
with coordinates
![]() $(u^1,\dots ,u^{15},x^1,\dots ,x^{6})$
, and consider fifteen 1-forms
$(u^1,\dots ,u^{15},x^1,\dots ,x^{6})$
, and consider fifteen 1-forms
![]() $\lambda ^1,\dots ,\lambda ^5$
on M given by
$\lambda ^1,\dots ,\lambda ^5$
on M given by
with
The rank 6 distribution
![]() ${\mathcal D}$
on M defined as
${\mathcal D}$
on M defined as ![]() has its Lie algebra of infinitesimal authomorphisms
has its Lie algebra of infinitesimal authomorphisms
![]() $\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of
$\mathfrak {aut}(\mathcal D)$
isomorphic to the Tanaka prolongation of ![]() , where
, where
![]() $(\rho ,S=\mathbb {R}^{6})$
is the 6-dimensional defining representation of
$(\rho ,S=\mathbb {R}^{6})$
is the 6-dimensional defining representation of
![]() $\mathfrak {n}_{00}=\mathfrak {gl}(6,\mathbb {R})$
, and
$\mathfrak {n}_{00}=\mathfrak {gl}(6,\mathbb {R})$
, and
![]() $(\tau ,R=\bigwedge ^2\mathbb {R}^6)$
is the
$(\tau ,R=\bigwedge ^2\mathbb {R}^6)$
is the
![]() $15$
-dimensional irreducible subrepresentation
$15$
-dimensional irreducible subrepresentation
![]() $\tau =\rho \wedge \rho $
of
$\tau =\rho \wedge \rho $
of
![]() $\mathfrak {n}_{00}$
.
$\mathfrak {n}_{00}$
.
The symmetry algebra
![]() $\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
$\mathfrak {aut}({\mathcal D})$
is isomorphic to the simple exceptional Lie algebra
![]() $\mathfrak {so}(7,6)$
,
$\mathfrak {so}(7,6)$
,
having the following natural gradation:
with
![]() $\mathfrak {n}_{-2}=R$
,
$\mathfrak {n}_{-2}=R$
,
![]() $\mathfrak {n}_{-1}=S$
,
$\mathfrak {n}_{-1}=S$
,
![]() $\mathfrak {n}_{1}=S^*$
,
$\mathfrak {n}_{1}=S^*$
,
![]() $\mathfrak {n}_{2}=R^*$
. The gradation in
$\mathfrak {n}_{2}=R^*$
. The gradation in
![]() $\mathfrak {so}(7,6)$
is inherited from the distribution structure
$\mathfrak {so}(7,6)$
is inherited from the distribution structure
![]() $(M,{\mathcal D})$
. The duality signs
$(M,{\mathcal D})$
. The duality signs
![]() $*$
at
$*$
at
![]() $R^*$
and
$R^*$
and
![]() $S^*$
above are with respect to the Killing form in
$S^*$
above are with respect to the Killing form in
![]() $\mathfrak {so}(7,6)$
.
$\mathfrak {so}(7,6)$
.
The contactification
![]() $(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
$(M,{\mathcal D})$
is locally the flat model for the parabolic geometry of type
![]() $(\mathfrak {so}(7,6),P)$
related to the following crossed Satake diagram:
$(\mathfrak {so}(7,6),P)$
related to the following crossed Satake diagram: ![]() .
.
Competing interests
The authors have no competing interest to declare.









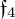


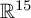
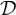




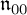
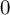
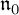
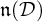
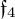
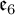




 ,
, ,
, , and
, and .
. , has the
, has the  , has the
, has the 