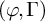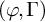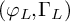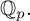1 Introduction
In [Reference Nakamura36] Nakamura generalized Kato’s p-adic local
![]() $\epsilon $
-conjecture [Reference Kato27, Reference Fukaya and Kato23] to the framework of
$\epsilon $
-conjecture [Reference Kato27, Reference Fukaya and Kato23] to the framework of
![]() $(\varphi ,\Gamma )$
-modules over the Robba ring (over
$(\varphi ,\Gamma )$
-modules over the Robba ring (over
![]() $\mathbb {Q}_p$
-affinoid algebras) and proved the essential parts of it for rigid analytic families of trianguline
$\mathbb {Q}_p$
-affinoid algebras) and proved the essential parts of it for rigid analytic families of trianguline
![]() $(\varphi ,\Gamma )$
-modules. The technical foundations for this had been laid by the work of Kedlaya, Pottharst and Xiao [Reference Kedlaya, Pottharst and Xiao28] who had established the fundamental theorems concerning their cohomology (finiteness, base change property, Tate duality, Euler-Poincaré formula) and Nakamura’s work [Reference Nakamura35], in which he generalized the theory of Bloch-Kato exponential maps and Perrin-Riou’s exponential maps in that framework.
$(\varphi ,\Gamma )$
-modules. The technical foundations for this had been laid by the work of Kedlaya, Pottharst and Xiao [Reference Kedlaya, Pottharst and Xiao28] who had established the fundamental theorems concerning their cohomology (finiteness, base change property, Tate duality, Euler-Poincaré formula) and Nakamura’s work [Reference Nakamura35], in which he generalized the theory of Bloch-Kato exponential maps and Perrin-Riou’s exponential maps in that framework.
Recently there has been much progress concerning
![]() $(\varphi _L,\Gamma _L)$
-modules over Lubin-Tate extensions [Reference Fourquaux21, Reference Kisin and Ren30, Reference Berger and Fourquaux6, Reference Fourquaux and Xie22, Reference Schneider and Venjakob45, Reference Schneider and Venjakob46]. In particular, the results by Steingart [Reference Steingart50, Reference Steingart51] regarding such
$(\varphi _L,\Gamma _L)$
-modules over Lubin-Tate extensions [Reference Fourquaux21, Reference Kisin and Ren30, Reference Berger and Fourquaux6, Reference Fourquaux and Xie22, Reference Schneider and Venjakob45, Reference Schneider and Venjakob46]. In particular, the results by Steingart [Reference Steingart50, Reference Steingart51] regarding such
![]() $(\varphi _L,\Gamma _L)$
-modules over families (finiteness, base change property, Euler-Poincaré formula, perfectness of Iwasawa cohomology) make it possible to study a version of Nakamura’s approach for L-analytic trianguline modules.
$(\varphi _L,\Gamma _L)$
-modules over families (finiteness, base change property, Euler-Poincaré formula, perfectness of Iwasawa cohomology) make it possible to study a version of Nakamura’s approach for L-analytic trianguline modules.
Let
![]() $L {\subseteq } {\mathbb {C}}_{p}$
be a finite extension of
$L {\subseteq } {\mathbb {C}}_{p}$
be a finite extension of
![]() ${\mathbb {Q}}_p$
and
${\mathbb {Q}}_p$
and
![]() $L_{\infty }$
a Lubin-Tate extension of L with Galois group
$L_{\infty }$
a Lubin-Tate extension of L with Galois group
![]() ${\Gamma }_{L} = \operatorname {Gal}(L_{\infty }/L)$
corresponding to a uniformiser
${\Gamma }_{L} = \operatorname {Gal}(L_{\infty }/L)$
corresponding to a uniformiser
![]() $\pi _L$
of the ring of integers
$\pi _L$
of the ring of integers
![]() $o_L$
of
$o_L$
of
![]() $L.$
A continuous representation of
$L.$
A continuous representation of
![]() $G_L$
on a finite dimensional L-vector space V is called L-analytic, if the semi-linear representation
$G_L$
on a finite dimensional L-vector space V is called L-analytic, if the semi-linear representation
![]() ${\mathbb {C}}_p\otimes _{\mathbb {Q}_p}V \cong \prod _{\sigma \colon L \to {\mathbb {C}}_p}{\mathbb {C}}_p\otimes _{L,\sigma }V$
is trivial at the components where
${\mathbb {C}}_p\otimes _{\mathbb {Q}_p}V \cong \prod _{\sigma \colon L \to {\mathbb {C}}_p}{\mathbb {C}}_p\otimes _{L,\sigma }V$
is trivial at the components where
![]() $\sigma \neq \operatorname {id}.$
By a theorem of Berger the category of L-analytic representations is equivalent to the category of étale L-analytic
$\sigma \neq \operatorname {id}.$
By a theorem of Berger the category of L-analytic representations is equivalent to the category of étale L-analytic
![]() $(\varphi _L,\Gamma _L)$
-modules over the Robba ring
$(\varphi _L,\Gamma _L)$
-modules over the Robba ring
![]() $\mathcal {R}_L$
(cf. [Reference Berger5]). Analyticity means here, that the action of the Lie group
$\mathcal {R}_L$
(cf. [Reference Berger5]). Analyticity means here, that the action of the Lie group
![]() $\Gamma _L$
is differentiable and the action of
$\Gamma _L$
is differentiable and the action of
![]() $\operatorname {Lie}(\Gamma _L)$
is (not only
$\operatorname {Lie}(\Gamma _L)$
is (not only
![]() $\mathbb {Q}_p$
-, but even) L-bilinear. For analytic
$\mathbb {Q}_p$
-, but even) L-bilinear. For analytic
![]() $(\varphi _L,\Gamma _L)$
-modules one can define analytic cohomology (see Section 4 for a precise definition). Finiteness of analytic cohomology allows us to attach to a family M of analytic
$(\varphi _L,\Gamma _L)$
-modules one can define analytic cohomology (see Section 4 for a precise definition). Finiteness of analytic cohomology allows us to attach to a family M of analytic
![]() $(\varphi _L,\Gamma _L)$
-modules over A a graded invertible line bundle
$(\varphi _L,\Gamma _L)$
-modules over A a graded invertible line bundle
![]() $\Delta _A(M)$
over A which is essentially the determinant of the analytic cohomology of M. Note that, for an L-analytic étale
$\Delta _A(M)$
over A which is essentially the determinant of the analytic cohomology of M. Note that, for an L-analytic étale
![]() $(\varphi _L,\Gamma _L)$
-module attached to some L-analytic Galois representation V of
$(\varphi _L,\Gamma _L)$
-module attached to some L-analytic Galois representation V of
![]() $G_L$
with coefficients in L, these analytic cohomology groups in general do not coincide with the Galois cohomology groups
$G_L$
with coefficients in L, these analytic cohomology groups in general do not coincide with the Galois cohomology groups
![]() $H^i(L,V)$
of V for
$H^i(L,V)$
of V for
![]() $i>0.$
Nonetheless they behave similarly to Galois cohomology and allow us to study certain invariants of V “at the identity component”. If M is the
$i>0.$
Nonetheless they behave similarly to Galois cohomology and allow us to study certain invariants of V “at the identity component”. If M is the
![]() $(\varphi _{L},\Gamma _{L})$
-module attached to an L-analytic de Rham representation
$(\varphi _{L},\Gamma _{L})$
-module attached to an L-analytic de Rham representation
![]() $V,$
then one can also attach an
$V,$
then one can also attach an
![]() $\varepsilon $
-constant to the “identity component” of
$\varepsilon $
-constant to the “identity component” of
![]() $D_{pst}(V),$
i.e., the
$D_{pst}(V),$
i.e., the
![]() $G_L$
-smooth vectors in
$G_L$
-smooth vectors in
![]() $\mathbf {B}_{st}\otimes _{L_0}V$
(which injects into the full
$\mathbf {B}_{st}\otimes _{L_0}V$
(which injects into the full
![]() $\mathbf {B}_{st}\otimes _{{\mathbb {Q}_p}}V$
). This can be generalised to the non-étale case as well (see Section 7.4 for details). The content of the analytic variant of the
$\mathbf {B}_{st}\otimes _{{\mathbb {Q}_p}}V$
). This can be generalised to the non-étale case as well (see Section 7.4 for details). The content of the analytic variant of the
![]() $\varepsilon $
-conjecture is a trivialisation of
$\varepsilon $
-conjecture is a trivialisation of
![]() $\Delta _A(M)$
which interpolates these
$\Delta _A(M)$
which interpolates these
![]() $\varepsilon $
-constants at the de Rham points, i.e., the points
$\varepsilon $
-constants at the de Rham points, i.e., the points
![]() $x \in \operatorname {Sp}(A)$
where the specialisation
$x \in \operatorname {Sp}(A)$
where the specialisation
![]() $M_x$
is de Rham.
$M_x$
is de Rham.
We formulate the following conjecture in a more general setting (and indicate in Remark 7.7 (ii) how to formulate a version of this conjecture for L-analytic
![]() $(\varphi _L,\Gamma _L)$
-modules over the character variety
$(\varphi _L,\Gamma _L)$
-modules over the character variety
![]() $\mathfrak {X}_{o_L}$
in the sense of Schneider-Teitelbaum).
$\mathfrak {X}_{o_L}$
in the sense of Schneider-Teitelbaum).
Conjecture (See Conjecture 7.6)
Choose a compatible system
![]() $u=(u_n)$
of
$u=(u_n)$
of
![]() $[\pi _L^n]$
-torsion points of the Lubin-Tate group and a generator
$[\pi _L^n]$
-torsion points of the Lubin-Tate group and a generator
![]() $t^{\prime }_0$
of the Tate module of its Cartier dual. Let K be a complete field extension of L containing
$t^{\prime }_0$
of the Tate module of its Cartier dual. Let K be a complete field extension of L containing
![]() $L^{ab}$
, and A an affinoid algebra over K. For each L-analytic
$L^{ab}$
, and A an affinoid algebra over K. For each L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_A$
satisfying condition (63) there exists a unique trivialisation
$\mathcal {R}_A$
satisfying condition (63) there exists a unique trivialisation
satisfying the following axioms:
-
(i) For any affinoid algebra B over A we have
under the canonical isomorphism $$ \begin{align*}\varepsilon_{A,u}(M)\otimes_A \operatorname{id}_B = \varepsilon_{B,u}(M\hat{\otimes}_AB)\end{align*} $$
$$ \begin{align*}\varepsilon_{A,u}(M)\otimes_A \operatorname{id}_B = \varepsilon_{B,u}(M\hat{\otimes}_AB)\end{align*} $$
 $\Delta _A(M)\otimes _AB \cong \Delta _B(M\hat {\otimes }_AB).$
$\Delta _A(M)\otimes _AB \cong \Delta _B(M\hat {\otimes }_AB).$
-
(ii)
 $\varepsilon _{A,u}$
is multiplicative in short exact sequences.
$\varepsilon _{A,u}$
is multiplicative in short exact sequences. -
(iii) For any
 $a \in o_L^\times $
we have
$a \in o_L^\times $
we have  $$ \begin{align*}\varepsilon_{A,a \cdot u}(M)=\delta_{\det M}(a)\varepsilon_{A,u}.\end{align*} $$
$$ \begin{align*}\varepsilon_{A,a \cdot u}(M)=\delta_{\det M}(a)\varepsilon_{A,u}.\end{align*} $$
-
(iv)
 $\varepsilon _{A,u}(M)$
is compatible with duality in the sense that for the dual module
$\varepsilon _{A,u}(M)$
is compatible with duality in the sense that for the dual module
 $\tilde {M}$
(see section 4.3) we have under the natural isomorphisms
$\tilde {M}$
(see section 4.3) we have under the natural isomorphisms $$ \begin{align*}\varepsilon_{A,u}(\tilde{M})^* \otimes h(\chi^{r_M}) = (-1)^{\dim_KH^0(M)}\Omega_{t^{\prime}_0}^{-r_{M}} \varepsilon_{A,-u}(M)\end{align*} $$
$$ \begin{align*}\varepsilon_{A,u}(\tilde{M})^* \otimes h(\chi^{r_M}) = (-1)^{\dim_KH^0(M)}\Omega_{t^{\prime}_0}^{-r_{M}} \varepsilon_{A,-u}(M)\end{align*} $$
 $\mathbf {1}_A \cong \mathbf {1}_A \otimes \mathbf {1}_A$
and
$\mathbf {1}_A \cong \mathbf {1}_A \otimes \mathbf {1}_A$
and
 $\Delta (M)\cong \Delta (\tilde {M})^* \otimes (A(r_M),0),$
where
$\Delta (M)\cong \Delta (\tilde {M})^* \otimes (A(r_M),0),$
where
 $h(\chi ^{r_M}) \colon A(r_M) \to A$
maps
$h(\chi ^{r_M}) \colon A(r_M) \to A$
maps
 $e_{\chi ^{r_M}}$
to
$e_{\chi ^{r_M}}$
to
 $1$
and
$1$
and
 $r_M$
denotes the rank of M over
$r_M$
denotes the rank of M over
 $\mathcal {R}_K$
.
$\mathcal {R}_K$
.
-
(v) For
 $L=\mathbb {Q}_p$
,
$L=\mathbb {Q}_p$
,
 $\pi _L=p$
and
$\pi _L=p$
and
 $u=(\zeta _{p^n}-1)_n$
the trivialisation coincides with that of Nakamura, in the sense of Proposition 8.7.
$u=(\zeta _{p^n}-1)_n$
the trivialisation coincides with that of Nakamura, in the sense of Proposition 8.7. -
(vi) Let
 $F/L$
be a finite subextension of
$F/L$
be a finite subextension of
 $K, M_0$
be a de Rham
$K, M_0$
be a de Rham
 $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
 $\mathcal {R}_F$
and
$\mathcal {R}_F$
and
 $M = K\hat {\otimes }_FM_0.$
Then where the isomorphism
$M = K\hat {\otimes }_FM_0.$
Then where the isomorphism $$ \begin{align*}\varepsilon_{K,u}(M)=\varepsilon^{dR}_{F,u}(M_0),\end{align*} $$
$$ \begin{align*}\varepsilon_{K,u}(M)=\varepsilon^{dR}_{F,u}(M_0),\end{align*} $$
 $\varepsilon ^{dR}_{F,u}(M_0): \mathbf {1}_K\xrightarrow {\cong } \Delta _K(M)$
is called the de Rham
$\varepsilon ^{dR}_{F,u}(M_0): \mathbf {1}_K\xrightarrow {\cong } \Delta _K(M)$
is called the de Rham
 $\varepsilon $
-isomorphism which is defined in (65) unconditionally using a generalized Bloch–Kato exponential and dual exponential map as well as the
$\varepsilon $
-isomorphism which is defined in (65) unconditionally using a generalized Bloch–Kato exponential and dual exponential map as well as the
 $\varepsilon $
-constant associated to
$\varepsilon $
-constant associated to
 $M_0$
in section 7.4.
$M_0$
in section 7.4.
While in the cyclotomic setting the
![]() $\epsilon $
-constants depend on the choice of a norm compatible system of p-power roots of unity, in the Lubin-Tate setting this is replaced by a compatible system of
$\epsilon $
-constants depend on the choice of a norm compatible system of p-power roots of unity, in the Lubin-Tate setting this is replaced by a compatible system of
![]() $\pi _L$
-power torsion points of the Lubin-Tate formal group, see Remarks 6.1, 6.3 for a comparison of both. We also fix a generator
$\pi _L$
-power torsion points of the Lubin-Tate formal group, see Remarks 6.1, 6.3 for a comparison of both. We also fix a generator
![]() $t^{\prime }_0$
of the Tate module of the Cartier dual of the Lubin Tate group which determines a certain period
$t^{\prime }_0$
of the Tate module of the Cartier dual of the Lubin Tate group which determines a certain period
![]() $\Omega _{t^{\prime }_0} \in \mathbb {C}_p$
(cf. [Reference Schneider and Teitelbaum43]). We prove parts of this conjecture for L-analytic trianguline
$\Omega _{t^{\prime }_0} \in \mathbb {C}_p$
(cf. [Reference Schneider and Teitelbaum43]). We prove parts of this conjecture for L-analytic trianguline
![]() $(\varphi _L,\Gamma _L)$
-modules. More precisely, we construct the
$(\varphi _L,\Gamma _L)$
-modules. More precisely, we construct the
![]() $\varepsilon $
-isomorphism for the Lubin-Tate deformation of a rank one, de Rham L-analytic
$\varepsilon $
-isomorphism for the Lubin-Tate deformation of a rank one, de Rham L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module M over some finite extension F of L
$(\varphi _L,\Gamma _L)$
-module M over some finite extension F of L
see Theorem 8.6. This lives over the rigid analytic character variety
![]() $\mathfrak {X}_{\Gamma _L}$
over L. The
$\mathfrak {X}_{\Gamma _L}$
over L. The
![]() $\mathbb {C}_p$
-points of this variety correspond to locally L-analytic characters
$\mathbb {C}_p$
-points of this variety correspond to locally L-analytic characters
![]() $\Gamma _L\to \mathbb {C}_p^\times .$
We refer to subsection 4.2 for the precise definition of the Lubin-Tate deformation
$\Gamma _L\to \mathbb {C}_p^\times .$
We refer to subsection 4.2 for the precise definition of the Lubin-Tate deformation
![]() $\mathbf {Dfm}(N)$
of a
$\mathbf {Dfm}(N)$
of a
![]() $(\varphi _L,\Gamma _L)$
-module N over
$(\varphi _L,\Gamma _L)$
-module N over
![]() $\mathcal {R}_K.$
Heuristically one can think of it as the base changed
$\mathcal {R}_K.$
Heuristically one can think of it as the base changed
![]() $(\varphi _L,\Gamma _L)$
-module
$(\varphi _L,\Gamma _L)$
-module
![]() $D(\Gamma _L,K)\hat {\otimes }_K N$
over the relative Robba ring
$D(\Gamma _L,K)\hat {\otimes }_K N$
over the relative Robba ring
![]() $D(\Gamma _L,K)\hat {\otimes }_K\mathcal {R}_K.$
But due to the complicated behaviour of completed tensor products over LF-spaces which are not Fréchet, it requires a more technical treatment. The correct point of view, which is used for the cyclotomic setting in earlier articles of Pottharst (but apparently neither consequently pursued nor carefully explained in [Reference Kedlaya, Pottharst and Xiao28, Def. 4.4.7, Thm. 4.4.8] unfortunately), consists of viewing this deformation as a sheaf of
$D(\Gamma _L,K)\hat {\otimes }_K\mathcal {R}_K.$
But due to the complicated behaviour of completed tensor products over LF-spaces which are not Fréchet, it requires a more technical treatment. The correct point of view, which is used for the cyclotomic setting in earlier articles of Pottharst (but apparently neither consequently pursued nor carefully explained in [Reference Kedlaya, Pottharst and Xiao28, Def. 4.4.7, Thm. 4.4.8] unfortunately), consists of viewing this deformation as a sheaf of
![]() $(\varphi _L,\Gamma _L)$
-modules over
$(\varphi _L,\Gamma _L)$
-modules over
![]() $\mathfrak {X}_{\Gamma _L},$
which is not affinoid and hence does not strictly speaking fit into the above Conjecture. Instead, the isomorphism
$\mathfrak {X}_{\Gamma _L},$
which is not affinoid and hence does not strictly speaking fit into the above Conjecture. Instead, the isomorphism
![]() $\varepsilon _{D(\Gamma _L),u}$
is a trivialisation of a line bundle over
$\varepsilon _{D(\Gamma _L),u}$
is a trivialisation of a line bundle over
![]() $\mathfrak {X}_{\Gamma _L}$
which restricts to an isomorphism of the conjectured type on each affinoid subdomain.
$\mathfrak {X}_{\Gamma _L}$
which restricts to an isomorphism of the conjectured type on each affinoid subdomain.
Philosophically, the L-analytic theory over Lubin-Tate extensions is one-dimensional and thus very similar to the cyclotomic case in the sense that
![]() $\Gamma _L$
is - although
$\Gamma _L$
is - although
![]() ${[L:\mathbb {Q}_p]}$
-dimensional over
${[L:\mathbb {Q}_p]}$
-dimensional over
![]() $\mathbb {Q}_p$
- one-dimensional as p-adic Lie group over L. Nevertheless, technically we have had to overcome serious difficulties. We are going to describe these differences compared to Nakamura’s work in the following.
$\mathbb {Q}_p$
- one-dimensional as p-adic Lie group over L. Nevertheless, technically we have had to overcome serious difficulties. We are going to describe these differences compared to Nakamura’s work in the following.
In the cyclotomic setting, Herr-complexes are formed with respect to the two operators
![]() $\varphi $
and
$\varphi $
and
![]() $\gamma -1$
for a topological generator
$\gamma -1$
for a topological generator
![]() $\gamma $
of the torsion-free part of
$\gamma $
of the torsion-free part of
![]() $\Gamma ;$
moreover, one can directly go over to the complex consisting of the fixed part under the torsion subgroup
$\Gamma ;$
moreover, one can directly go over to the complex consisting of the fixed part under the torsion subgroup
![]() $\Delta $
of
$\Delta $
of
![]() $\Gamma $
. In the Lubin-Tate setting (with
$\Gamma $
. In the Lubin-Tate setting (with
![]() $L\neq {\Bbb Q}$
) there is no intrinsic counterpart of
$L\neq {\Bbb Q}$
) there is no intrinsic counterpart of
![]() $\gamma $
as one needs at least
$\gamma $
as one needs at least
![]() $[L:\mathbb {Q}_p]$
elements to generate the (torsion-free part of)
$[L:\mathbb {Q}_p]$
elements to generate the (torsion-free part of)
![]() $\Gamma _L$
topologically. So instead we make use of Fourier theory and the Lubin-Tate isomorphism à la Schneider and Teitelbaum [Reference Schneider and Teitelbaum43]
$\Gamma _L$
topologically. So instead we make use of Fourier theory and the Lubin-Tate isomorphism à la Schneider and Teitelbaum [Reference Schneider and Teitelbaum43]
over a huge field extension K of L, over which the character variety
![]() $\mathfrak {X}_{\Gamma _n}$
for the subgroup of n-th higher units
$\mathfrak {X}_{\Gamma _n}$
for the subgroup of n-th higher units
![]() $\Gamma _n\cong o_L$
of
$\Gamma _n\cong o_L$
of
![]() $\Gamma _L$
can be identified with the open unit disk
$\Gamma _L$
can be identified with the open unit disk
![]() $\mathbf {B}$
for n sufficiently big. Via this isomorphism we can now choose
$\mathbf {B}$
for n sufficiently big. Via this isomorphism we can now choose
![]() ${{\mathfrak {Z}}_n}\in D(\Gamma _n,K) $
corresponding to the choice of a coordinate of
${{\mathfrak {Z}}_n}\in D(\Gamma _n,K) $
corresponding to the choice of a coordinate of
![]() $\mathbf {B}$
. The generalized Herr-complex in the Lubin-Tate setting can thus be formed using the two operators
$\mathbf {B}$
. The generalized Herr-complex in the Lubin-Tate setting can thus be formed using the two operators
![]() $\varphi _L$
and
$\varphi _L$
and
![]() ${\mathfrak {Z}}_n.$
Unfortunately, in contrast to
${\mathfrak {Z}}_n.$
Unfortunately, in contrast to
![]() $\Delta \subseteq \Gamma _{\mathbb {Q}_p}$
, the remaining quotient
$\Delta \subseteq \Gamma _{\mathbb {Q}_p}$
, the remaining quotient
![]() $\Gamma _L/\Gamma _n$
in general cannot be identified with a subgroup of
$\Gamma _L/\Gamma _n$
in general cannot be identified with a subgroup of
![]() $\Gamma _L$
, whence we cannot take
$\Gamma _L$
, whence we cannot take
![]() $\Gamma _L/\Gamma _n$
-invariants as before, but have to circumvent this problem.
$\Gamma _L/\Gamma _n$
-invariants as before, but have to circumvent this problem.
An important step for our approach consists of establishing the analogue of local Tate duality for analytic cohomology, see subsection 4.3. In contrast to [Reference Nakamura36] we find an intrinsic way to normalize our trace map without any comparison to Galois cohomology (which is not available anyway as we indicated); nevertheless for
![]() $L=\mathbb {Q}_p$
our choice coincides with that of Nakamura (for an appropriate choice of period
$L=\mathbb {Q}_p$
our choice coincides with that of Nakamura (for an appropriate choice of period
![]() $ \Omega $
).
$ \Omega $
).
Another price we have to pay is the fact that even the minimal choice for K is no longer spherically complete, which means that the functional analysis requires some additional care. For the explicit descent calculation Lemma 8.16 we make use of the explicit reciprocity law from [Reference Schneider and Venjakob45].
Contrary to the cyclotomic case, it seems difficult to establish integral results in the analytic case. On the one hand the “dualizing character”
![]() $\chi $
used to establish Tate duality has Frobenius action given by
$\chi $
used to establish Tate duality has Frobenius action given by
![]() $\frac {\pi _L}{q}$
and hence does not make sense integrally (unless
$\frac {\pi _L}{q}$
and hence does not make sense integrally (unless
![]() $L=\mathbb {Q}_p$
), on the other hand the period
$L=\mathbb {Q}_p$
), on the other hand the period
![]() $\Omega $
is not a unit (unless
$\Omega $
is not a unit (unless
![]() $L=\mathbb {Q}_p$
). The L-analytic distribution algebra
$L=\mathbb {Q}_p$
). The L-analytic distribution algebra
![]() $D(\Gamma _L,L)$
contains the ring
$D(\Gamma _L,L)$
contains the ring
![]() $\Lambda _{\mathfrak {X}_{\Gamma _L}}$
of power-bounded functions on the character variety. It is not known whether
$\Lambda _{\mathfrak {X}_{\Gamma _L}}$
of power-bounded functions on the character variety. It is not known whether ![]() Paradoxically, the Iwasawa algebra
Paradoxically, the Iwasawa algebra ![]() is dense inside both the d-dimensional
is dense inside both the d-dimensional
![]() $\mathbb {Q}_p$
-analytic distribution algebra and the
$\mathbb {Q}_p$
-analytic distribution algebra and the
![]() $1$
-dimensional L-analytic distribution algebra making it unclear how to descend to integral results even under the assumption
$1$
-dimensional L-analytic distribution algebra making it unclear how to descend to integral results even under the assumption ![]()
The structure of the paper is as follows: In section 3 we introduce (analytic)
![]() $(\varphi _L,\Gamma _L)$
-modules. In section 4 we introduce and study analytic cohomology of analytic
$(\varphi _L,\Gamma _L)$
-modules. In section 4 we introduce and study analytic cohomology of analytic
![]() $(\varphi _L,\Gamma _L)$
-modules and recall the main results of [Reference Steingart50] while providing some generalisations suited to our needs. Furthermore, we develop an analogue of Tate duality for analytic cohomology. In section 5 we develop an analogue of the Bloch-Kato (dual) exponential map for analytic cohomology. We recall classical
$(\varphi _L,\Gamma _L)$
-modules and recall the main results of [Reference Steingart50] while providing some generalisations suited to our needs. Furthermore, we develop an analogue of Tate duality for analytic cohomology. In section 5 we develop an analogue of the Bloch-Kato (dual) exponential map for analytic cohomology. We recall classical
![]() $\varepsilon $
-constants in section 6 and state the conjecture in Section 7. Section 8 is dedicated to proving the main result. In the Appendix we adapt Nakamura’s density argument to the Lubin-Tate setting.
$\varepsilon $
-constants in section 6 and state the conjecture in Section 7. Section 8 is dedicated to proving the main result. In the Appendix we adapt Nakamura’s density argument to the Lubin-Tate setting.
2 Notation
We denote by
![]() $\mathbb {N}$
the natural numbers including
$\mathbb {N}$
the natural numbers including
![]() $0.$
$0.$
Let
![]() $\mathbb {Q}_p \subseteq L \subset \mathbb {C}_p$
be a field of finite degree d over
$\mathbb {Q}_p \subseteq L \subset \mathbb {C}_p$
be a field of finite degree d over
![]() $\mathbb {Q}_p$
,
$\mathbb {Q}_p$
,
![]() $o_L$
the ring of integers of L,
$o_L$
the ring of integers of L,
![]() $\pi _L \in o_L$
a fixed prime element,
$\pi _L \in o_L$
a fixed prime element,
![]() $k_L = o_L/\pi _L o_L$
the residue field,
$k_L = o_L/\pi _L o_L$
the residue field,
![]() $q := |k_L|$
and e the absolute ramification index of L. We always use the absolute value
$q := |k_L|$
and e the absolute ramification index of L. We always use the absolute value
![]() $|\ |$
on
$|\ |$
on
![]() $\mathbb {C}_p$
which is normalized by
$\mathbb {C}_p$
which is normalized by
![]() $|\pi _L| = q^{-1}$
. This choice of normalisation is consistent with [Reference Colmez15] and [Reference Schneider and Venjakob46]. We normalize the reciprocity map of local class field theory such that
$|\pi _L| = q^{-1}$
. This choice of normalisation is consistent with [Reference Colmez15] and [Reference Schneider and Venjakob46]. We normalize the reciprocity map of local class field theory such that
![]() $\pi _L$
is sent to the geometric Frobenius.
$\pi _L$
is sent to the geometric Frobenius.
We fix a Lubin-Tate formal
![]() $o_L$
-module
$o_L$
-module
![]() $LT = LT_{\pi _L}$
over
$LT = LT_{\pi _L}$
over
![]() $o_L$
corresponding to the prime element
$o_L$
corresponding to the prime element
![]() $\pi _L$
. We always identify
$\pi _L$
. We always identify
![]() $LT$
with the open unit disk around zero, which gives us a global coordinate Z on
$LT$
with the open unit disk around zero, which gives us a global coordinate Z on
![]() $LT$
. The
$LT$
. The
![]() $o_L$
-action then is given by formal power series
$o_L$
-action then is given by formal power series
![]() $[a](Z) \in o_L[[Z]]$
. For simplicity the formal group law will be denoted by
$[a](Z) \in o_L[[Z]]$
. For simplicity the formal group law will be denoted by
![]() $+_{LT}$
.
$+_{LT}$
.
The power series
![]() $\frac {\partial (X +_{LT} Y)}{\partial Y}_{|(X,Y) = (Z,0)}$
is a unit in
$\frac {\partial (X +_{LT} Y)}{\partial Y}_{|(X,Y) = (Z,0)}$
is a unit in
![]() $o_L[[Z]]$
and we let
$o_L[[Z]]$
and we let
![]() $g_{LT}(Z)$
denote its inverse. Then
$g_{LT}(Z)$
denote its inverse. Then
![]() $g_{LT}(Z) dZ$
is, up to scalars, the unique invariant differential form on
$g_{LT}(Z) dZ$
is, up to scalars, the unique invariant differential form on
![]() $LT$
([Reference Hazewinkel24] §5.8). We also let
$LT$
([Reference Hazewinkel24] §5.8). We also let
denote the unique formal power series in
![]() $L[[Z]]$
whose formal derivative is
$L[[Z]]$
whose formal derivative is
![]() $g_{LT}$
. This
$g_{LT}$
. This
![]() $\log _{LT}$
is the logarithm of
$\log _{LT}$
is the logarithm of
![]() $LT$
in the sense of [Reference Lang32, §8.6] and converges on the maximal ideal in
$LT$
in the sense of [Reference Lang32, §8.6] and converges on the maximal ideal in
![]() ${o_{\mathbb {C}_p}}$
(by §8.6, Lemma 3 (ii) ibid.). By
${o_{\mathbb {C}_p}}$
(by §8.6, Lemma 3 (ii) ibid.). By
![]() $\exp _{LT}:=\log _{LT}^{-1}$
in
$\exp _{LT}:=\log _{LT}^{-1}$
in
![]() $L[[Z]]$
we denote the inverse power series of
$L[[Z]]$
we denote the inverse power series of
![]() $\log _{LT} $
, i.e., satisfying
$\log _{LT} $
, i.e., satisfying
![]() $\log _{LT}\circ \exp _{LT}(Z)=\exp _{LT}\circ \log _{LT}(Z)=Z.$
Footnote
1
$\log _{LT}\circ \exp _{LT}(Z)=\exp _{LT}\circ \log _{LT}(Z)=Z.$
Footnote
1
In particular,
![]() $g_{LT}dZ = d\log _{LT}$
. The invariant derivation
$g_{LT}dZ = d\log _{LT}$
. The invariant derivation
![]() $\partial _{\mathrm {inv}}$
corresponding to the form
$\partial _{\mathrm {inv}}$
corresponding to the form
![]() $d\log _{LT}$
is determined by
$d\log _{LT}$
is determined by
and hence is given by
For any
![]() $a \in o_L$
we have
$a \in o_L$
we have
([Reference Lang32] 8.6 Lemma 2).
Let
![]() $T_{\pi }$
be the Tate module of
$T_{\pi }$
be the Tate module of
![]() $LT$
. Then
$LT$
. Then
![]() $T_{\pi }$
is a free
$T_{\pi }$
is a free
![]() $o_L$
-module of rank one and we choose a generator
$o_L$
-module of rank one and we choose a generator
![]() $u=(u_n)_{n\in \mathbb {N}}$
where
$u=(u_n)_{n\in \mathbb {N}}$
where
![]() $u_0=0$
,
$u_0=0$
,
![]() $u_1\neq 0$
and, for all
$u_1\neq 0$
and, for all
![]() $n,$
we have
$n,$
we have
![]() $u_n\in \mathfrak {m}_{\mathbb {C}_p}$
as well as
$u_n\in \mathfrak {m}_{\mathbb {C}_p}$
as well as
![]() $[\pi _L](u_{n+1})=u_n.$
Then the action of
$[\pi _L](u_{n+1})=u_n.$
Then the action of
![]() $G_L := \operatorname {Gal}(\overline {L}/L)$
on
$G_L := \operatorname {Gal}(\overline {L}/L)$
on
![]() $T_{\pi }$
is given by a continuous character
$T_{\pi }$
is given by a continuous character
![]() $\chi _{LT} : G_L \longrightarrow o_L^\times $
. Let
$\chi _{LT} : G_L \longrightarrow o_L^\times $
. Let
![]() $T_{\pi }'$
denote the Tate module of the p-divisible group Cartier dual to
$T_{\pi }'$
denote the Tate module of the p-divisible group Cartier dual to
![]() $LT$
with period
$LT$
with period
![]() $\Omega _{t_0'}\in \widehat {L^{ab}}$
, which again is a free
$\Omega _{t_0'}\in \widehat {L^{ab}}$
, which again is a free
![]() $o_L$
-module of rank one and where
$o_L$
-module of rank one and where
![]() $t_0'$
is a generator. The Galois action on
$t_0'$
is a generator. The Galois action on
![]() $T_{\pi }'\cong T_{\pi }^*(1)$
is given by the continuous character
$T_{\pi }'\cong T_{\pi }^*(1)$
is given by the continuous character
![]() $\tau := \chi _{cyc}\cdot \chi _{LT}^{-1}$
, where
$\tau := \chi _{cyc}\cdot \chi _{LT}^{-1}$
, where
![]() $\chi _{cyc}$
is the cyclotomic character. As mentioned in [Reference Boxall8, §1] and [Reference Schneider and Teitelbaum42, §3] it follows from the work of Tate on p-divisible groups that we have natural
$\chi _{cyc}$
is the cyclotomic character. As mentioned in [Reference Boxall8, §1] and [Reference Schneider and Teitelbaum42, §3] it follows from the work of Tate on p-divisible groups that we have natural
![]() $o_L$
-linear isomorphisms
$o_L$
-linear isomorphisms
where the last isomorphism is induced by Pontryagin duality and the adjunction between
![]() $Hom$
and
$Hom$
and
![]() $\otimes .$
According to the proof of [Reference Boxall8, Lem. 13] the above composite sends
$\otimes .$
According to the proof of [Reference Boxall8, Lem. 13] the above composite sends
![]() $at_0'$
to the map sending
$at_0'$
to the map sending
![]() $u\otimes \frac {1}{\pi _L^n}$
to
$u\otimes \frac {1}{\pi _L^n}$
to
![]() $\eta _{t_0'}(a,u_n)$
, where, for
$\eta _{t_0'}(a,u_n)$
, where, for
![]() $x\in o_L$
, we define
$x\in o_L$
, we define
![]() $\eta _{t_0'}(x,Z):=\exp \left (\Omega _{t_0'} x\log _{LT}(Z)\right )\in 1+Zo_{\widehat {L_\infty }}[[Z]]$
; when the choice of
$\eta _{t_0'}(x,Z):=\exp \left (\Omega _{t_0'} x\log _{LT}(Z)\right )\in 1+Zo_{\widehat {L_\infty }}[[Z]]$
; when the choice of
![]() $t_0'$
is clear from the context, we often omit this index from
$t_0'$
is clear from the context, we often omit this index from
![]() $\Omega _{t_0'}$
or
$\Omega _{t_0'}$
or
![]() $\eta _{t_0'}(x,Z)$
.
$\eta _{t_0'}(x,Z)$
.
Our constructions will depend crucially on the choices of u and
![]() $t_0'$
, which determine the period
$t_0'$
, which determine the period
![]() $\Omega = \Omega _{t_0'}.$
By (4) these two choices automatically determine a system
$\Omega = \Omega _{t_0'}.$
By (4) these two choices automatically determine a system
of compatible p-power roots of unity.Footnote
2
In the cyclotomic case where
![]() $LT = \mathbb {G}_m$
it suffices to fix a choice of compatible p-power roots of unity because one can then take the identity as a canonical generator
$LT = \mathbb {G}_m$
it suffices to fix a choice of compatible p-power roots of unity because one can then take the identity as a canonical generator
![]() $t_0'$
of
$t_0'$
of
![]() $T_{\pi }'=\operatorname {Hom}(\mathbb {G}_m,\mathbb {G}_m)$
.
$T_{\pi }'=\operatorname {Hom}(\mathbb {G}_m,\mathbb {G}_m)$
.
For
![]() $n \geq 0$
we let
$n \geq 0$
we let
![]() $L_n/L$
denote the extension (in
$L_n/L$
denote the extension (in
![]() $\mathbb {C}_p$
) generated by the
$\mathbb {C}_p$
) generated by the
![]() $\pi _L^n$
-torsion points of
$\pi _L^n$
-torsion points of
![]() $LT$
, and we put
$LT$
, and we put
![]() $L_\infty := \bigcup _n L_n$
. The extension
$L_\infty := \bigcup _n L_n$
. The extension
![]() $L_\infty /L$
is Galois. We let
$L_\infty /L$
is Galois. We let
![]() $\Gamma _L := \operatorname {Gal}(L_\infty /L)$
and
$\Gamma _L := \operatorname {Gal}(L_\infty /L)$
and
![]() $H_L := \operatorname {Gal}(\overline {L}/L_\infty )$
. The Lubin-Tate character
$H_L := \operatorname {Gal}(\overline {L}/L_\infty )$
. The Lubin-Tate character
![]() $\chi _{LT}$
induces an isomorphism
$\chi _{LT}$
induces an isomorphism
![]() $\Gamma _L \xrightarrow {\cong } o_L^\times $
. Note that by [Reference Berger, Schneider and Xie7, Rem. 1.17] we have
$\Gamma _L \xrightarrow {\cong } o_L^\times $
. Note that by [Reference Berger, Schneider and Xie7, Rem. 1.17] we have
![]() $N_{L/{\Bbb Q}_p}\circ \chi _{LT}=\chi _{cyc}$
if and only if
$N_{L/{\Bbb Q}_p}\circ \chi _{LT}=\chi _{cyc}$
if and only if
![]() $N_{L/{\Bbb Q}_p}(\pi _L)\in p^{\mathbb {Z}}.$
$N_{L/{\Bbb Q}_p}(\pi _L)\in p^{\mathbb {Z}}.$
Note that we have homomorphisms
![]() $o_L\to 1+Zo_{\widehat {L_\infty }}[[Z]],\; x\mapsto \eta (x,Z),$
and
$o_L\to 1+Zo_{\widehat {L_\infty }}[[Z]],\; x\mapsto \eta (x,Z),$
and
![]() $LT\to \hat {\mathbb {G}}_m,\; Z \mapsto \eta (x,Z)$
, respectively. For a
$LT\to \hat {\mathbb {G}}_m,\; Z \mapsto \eta (x,Z)$
, respectively. For a
![]() $\pi _L^n$
-torsion point a (whence
$\pi _L^n$
-torsion point a (whence
![]() $p^m$
-torsion with
$p^m$
-torsion with
![]() $m=\lceil \frac {n}{e}\rceil $
being the smallest integer greater or equal to
$m=\lceil \frac {n}{e}\rceil $
being the smallest integer greater or equal to
![]() $\frac {n}{e}$
) we thus obtain a character
$\frac {n}{e}$
) we thus obtain a character
![]() $o_L\to \mathbb {Z}_p[\zeta _{p^m}]^\times , x\mapsto \eta (x,a),$
of finite order. In particular
$o_L\to \mathbb {Z}_p[\zeta _{p^m}]^\times , x\mapsto \eta (x,a),$
of finite order. In particular
![]() $\eta (x,u_n)$
belongs to
$\eta (x,u_n)$
belongs to
![]() $\mu _{p^m}$
for any
$\mu _{p^m}$
for any
![]() $x\in o_L.$
If
$x\in o_L.$
If
![]() $\gamma \in \Gamma _L$
, we have
$\gamma \in \Gamma _L$
, we have
![]() $\gamma \eta (x,Z)=\eta (\chi _{LT}(\gamma )x,Z), $
while
$\gamma \eta (x,Z)=\eta (\chi _{LT}(\gamma )x,Z), $
while
![]() $\varphi (\eta (x,Z))= \eta (\pi _Lx,Z).$
$\varphi (\eta (x,Z))= \eta (\pi _Lx,Z).$
Remark 2.1. Since for
![]() $\sigma $
in
$\sigma $
in
![]() $G_L, $
one has
$G_L, $
one has
![]() $\sigma (\Omega ) =\Omega \tau (\sigma )$
by [Reference Schneider and Venjakob46, Lem. 4.1.24], it follows that
$\sigma (\Omega ) =\Omega \tau (\sigma )$
by [Reference Schneider and Venjakob46, Lem. 4.1.24], it follows that
![]() ${^\sigma \eta (x,Z)}=\eta (x\tau (\sigma ),Z)=\eta (x,[\tau (\sigma )](Z))$
, if we let act
${^\sigma \eta (x,Z)}=\eta (x\tau (\sigma ),Z)=\eta (x,[\tau (\sigma )](Z))$
, if we let act
![]() $G_L$
on the coefficients only, and
$G_L$
on the coefficients only, and
![]() $\sigma ( \eta (x,Z))=\eta (x\tau (\sigma ),[\chi _{LT}(\sigma )](Z))=\eta (x,[\chi _{cyc}(\sigma )](Z))$
, if we let act
$\sigma ( \eta (x,Z))=\eta (x\tau (\sigma ),[\chi _{LT}(\sigma )](Z))=\eta (x,[\chi _{cyc}(\sigma )](Z))$
, if we let act
![]() $G_L$
on the coefficients and on the variable. In particular,
$G_L$
on the coefficients and on the variable. In particular,
![]() $\sigma (\eta (x,u_n))=\eta (x\tau (\sigma ),[\chi _{LT}(\sigma )](u_n))=\eta (x,[\chi _{cyc}(\sigma )](u_n))=\eta (x\chi _{cyc}(\sigma ),u_n)=\eta (x,u_n)^{\chi _{cyc}(\sigma )}.$
Moreover, for a fixed choice
$\sigma (\eta (x,u_n))=\eta (x\tau (\sigma ),[\chi _{LT}(\sigma )](u_n))=\eta (x,[\chi _{cyc}(\sigma )](u_n))=\eta (x\chi _{cyc}(\sigma ),u_n)=\eta (x,u_n)^{\chi _{cyc}(\sigma )}.$
Moreover, for a fixed choice
![]() $\zeta _{p^n}$
of a primitive
$\zeta _{p^n}$
of a primitive
![]() $p^n$
th root of unity, there is a unique homomorphism
$p^n$
th root of unity, there is a unique homomorphism
![]() $\beta _{u_n}:o_L\to \mathbb {Z}/p^n\mathbb {Z}$
such that the following diagram is commutative
$\beta _{u_n}:o_L\to \mathbb {Z}/p^n\mathbb {Z}$
such that the following diagram is commutative

i.e.,
![]() $\eta (x,u_n)=\zeta _{p^n}^{\beta _{u_n}(x)}.$
One easily checks that
$\eta (x,u_n)=\zeta _{p^n}^{\beta _{u_n}(x)}.$
One easily checks that
![]() $\beta _{u_n}(\chi _{cyc}(\sigma )x)=\chi _{cyc}(\sigma )\cdot \beta _{u_n}(x).$
$\beta _{u_n}(\chi _{cyc}(\sigma )x)=\chi _{cyc}(\sigma )\cdot \beta _{u_n}(x).$
Henceforth we use the same notation as in [Reference Schneider and Venjakob45]. In particular, the ring endomorphisms induced by sending Z to
![]() $[\pi _L](Z)$
are called
$[\pi _L](Z)$
are called
![]() $\varphi _L$
where applicable; e.g. for the ring
$\varphi _L$
where applicable; e.g. for the ring
![]() $\mathscr {A}_L$
defined to be the
$\mathscr {A}_L$
defined to be the
![]() $\pi _L$
-adic completion of
$\pi _L$
-adic completion of
![]() $o_L[[Z]][Z^{-1}]$
, or
$o_L[[Z]][Z^{-1}]$
, or
![]() $\mathscr {B}_L := \mathscr {A}_L[\pi _L^{-1}]$
which denotes the field of fractions of
$\mathscr {B}_L := \mathscr {A}_L[\pi _L^{-1}]$
which denotes the field of fractions of
![]() $\mathscr {A}_L$
. Recall that we also have introduced the unique additive endomorphism
$\mathscr {A}_L$
. Recall that we also have introduced the unique additive endomorphism
![]() $\psi _L$
of
$\psi _L$
of
![]() $\mathscr {B}_L$
(and then
$\mathscr {B}_L$
(and then
![]() $\mathscr {A}_L$
) which satisfies
$\mathscr {A}_L$
) which satisfies
Moreover, the projection formula
as well as the formula
hold. An étale
![]() $(\varphi _L,\Gamma _L)$
-module M comes with a Frobenius operator
$(\varphi _L,\Gamma _L)$
-module M comes with a Frobenius operator
![]() $\varphi _M$
and an induced operator denoted by
$\varphi _M$
and an induced operator denoted by
![]() $\psi _M$
.
$\psi _M$
.
For a perfectoid field extension F of L in the sense of [Reference Schneider41, Section 1.4] let
![]() ${o_{F^\flat } := \varprojlim o_{F}/p o_{F}}$
with the transition maps being given by the Frobenius
${o_{F^\flat } := \varprojlim o_{F}/p o_{F}}$
with the transition maps being given by the Frobenius
![]() $\varphi (a) = a^p$
. We may also identify
$\varphi (a) = a^p$
. We may also identify
![]() $o_{F^\flat }$
with
$o_{F^\flat }$
with
![]() $\varprojlim o_{F}/\pi _L o_{F}$
with the transition maps being given by the q-Frobenius
$\varprojlim o_{F}/\pi _L o_{F}$
with the transition maps being given by the q-Frobenius
![]() $\varphi _q (a) = a^q$
. We recall that
$\varphi _q (a) = a^q$
. We recall that
![]() $\widehat {L_\infty }$
and
$\widehat {L_\infty }$
and
![]() $\mathbb {C}_p$
are perfectoid and that
$\mathbb {C}_p$
are perfectoid and that
![]() $o_{\mathbb {C}_p^\flat }$
is a complete valuation ring with residue field
$o_{\mathbb {C}_p^\flat }$
is a complete valuation ring with residue field
![]() $\overline {\mathbb {F}_p}$
and its field of fractions
$\overline {\mathbb {F}_p}$
and its field of fractions
![]() $\mathbb {C}_p^\flat = \varprojlim \mathbb {C}_p$
is algebraically closed of characteristic p (cf. [Reference Schneider41, Lemma 1.4.6,Proposition 1.4.7 and Lemma 1.4.10, Proposition 1.4.12]). Let
$\mathbb {C}_p^\flat = \varprojlim \mathbb {C}_p$
is algebraically closed of characteristic p (cf. [Reference Schneider41, Lemma 1.4.6,Proposition 1.4.7 and Lemma 1.4.10, Proposition 1.4.12]). Let
![]() $\mathfrak {m}_{\mathbb {C}_p^\flat }$
denote the maximal ideal in
$\mathfrak {m}_{\mathbb {C}_p^\flat }$
denote the maximal ideal in
![]() $o_{\mathbb {C}_p^\flat }$
. The q-Frobenius
$o_{\mathbb {C}_p^\flat }$
. The q-Frobenius
![]() $\varphi _q$
first extends by functoriality to the rings of the Witt vectors
$\varphi _q$
first extends by functoriality to the rings of the Witt vectors
![]() $W(o_{\mathbb {C}_p^\flat }) \subseteq W(\mathbb {C}_p^\flat )$
and then
$W(o_{\mathbb {C}_p^\flat }) \subseteq W(\mathbb {C}_p^\flat )$
and then
![]() $o_L$
-linearly to
$o_L$
-linearly to
![]() $W(o_{\mathbb {C}_p^\flat })_L := W(o_{\mathbb {C}_p^\flat }) \otimes _{o_{L_0}} o_L \subseteq W(\mathbb {C}_p^\flat )_L := W(\mathbb {C}_p^\flat ) \otimes _{o_{L_0}} o_L$
, where
$W(o_{\mathbb {C}_p^\flat })_L := W(o_{\mathbb {C}_p^\flat }) \otimes _{o_{L_0}} o_L \subseteq W(\mathbb {C}_p^\flat )_L := W(\mathbb {C}_p^\flat ) \otimes _{o_{L_0}} o_L$
, where
![]() $L_0$
is the maximal unramified subextension of L. The Galois group
$L_0$
is the maximal unramified subextension of L. The Galois group
![]() $G_L$
obviously acts on
$G_L$
obviously acts on
![]() $\mathbb {C}_p^\flat $
and
$\mathbb {C}_p^\flat $
and
![]() $W(\mathbb {C}_p^\flat )_L$
by automorphisms commuting with
$W(\mathbb {C}_p^\flat )_L$
by automorphisms commuting with
![]() $\varphi _q$
. This
$\varphi _q$
. This
![]() $G_L$
-action is continuous for the weak topology on
$G_L$
-action is continuous for the weak topology on
![]() $W(\mathbb {C}_p^\flat )_L$
(cf. [Reference Schneider41] Lemma 1.5.3).
$W(\mathbb {C}_p^\flat )_L$
(cf. [Reference Schneider41] Lemma 1.5.3).
Sometimes we omit the index
![]() $q, L,$
or M from the Frobenius operator, but we always write
$q, L,$
or M from the Frobenius operator, but we always write
![]() $\varphi _p$
when dealing with the p-Frobenius.
$\varphi _p$
when dealing with the p-Frobenius.
Evaluation of the global coordinate Z of
![]() $LT$
at
$LT$
at
![]() $\pi _L$
-power torsion points induces a map (not a homomorphism of abelian groups)
$\pi _L$
-power torsion points induces a map (not a homomorphism of abelian groups)
![]() $\iota : T_\pi \longrightarrow o_{\mathbb {C}_p^\flat }$
. Namely, if
$\iota : T_\pi \longrightarrow o_{\mathbb {C}_p^\flat }$
. Namely, if
![]() $t= (z_n)_{n\geq 1} \in T_\pi $
with
$t= (z_n)_{n\geq 1} \in T_\pi $
with
![]() $[\pi _L](z_{n+1}) = z_n$
and
$[\pi _L](z_{n+1}) = z_n$
and
![]() $[\pi _L](z_1) = 0$
, then
$[\pi _L](z_1) = 0$
, then
![]() $z_{n+1}^q \equiv z_n \bmod \pi _L$
and hence
$z_{n+1}^q \equiv z_n \bmod \pi _L$
and hence
![]() $\iota (t) := (z_n \bmod \pi _L)_n \in o_{\mathbb {C}_p^\flat }$
. As before we fix an
$\iota (t) := (z_n \bmod \pi _L)_n \in o_{\mathbb {C}_p^\flat }$
. As before we fix an
![]() $o_L$
-generator u of
$o_L$
-generator u of
![]() $T_\pi $
and put
$T_\pi $
and put
![]() $\omega _u:=\iota (u).$
Then there exists a (unique) lift
$\omega _u:=\iota (u).$
Then there exists a (unique) lift
![]() $Z_u \in W(o_{\mathbb {C}_p^\flat })_L$
of
$Z_u \in W(o_{\mathbb {C}_p^\flat })_L$
of
![]() $\omega _u$
satisfying (cf. [Reference Schneider and Venjakob45, Lem. 4.1])
$\omega _u$
satisfying (cf. [Reference Schneider and Venjakob45, Lem. 4.1])
-
(i) if
 $u'=au$
with
$u'=au$
with
 $a \in o_L^\times $
denotes another generator of
$a \in o_L^\times $
denotes another generator of
 $T_\pi $
, then
$T_\pi $
, then
 $ Z_{u'}=[a](Z_u ) $
is the corresponding lift;
$ Z_{u'}=[a](Z_u ) $
is the corresponding lift; -
(ii)
 $\phi _q(Z_u) = [\pi _L](Z_u)$
;
$\phi _q(Z_u) = [\pi _L](Z_u)$
; -
(iii)
 $\sigma (Z_u)=[\chi _{LT}(\sigma )](Z_u)$
for any
$\sigma (Z_u)=[\chi _{LT}(\sigma )](Z_u)$
for any
 $\sigma \in G_L$
.
$\sigma \in G_L$
.
By sending Z to
![]() $Z_u\in W(o_{\mathbb {C}_p^\flat })_L$
we obtain an
$Z_u\in W(o_{\mathbb {C}_p^\flat })_L$
we obtain an
![]() $G_L$
-equivariant, Frobenius compatible embedding of rings
$G_L$
-equivariant, Frobenius compatible embedding of rings
Let
![]() $K\subseteq \mathbb {C}_p$
be a complete subfield containing
$K\subseteq \mathbb {C}_p$
be a complete subfield containing
![]() $L_\infty $
and
$L_\infty $
and
![]() $\Omega ,$
i.e., the minimal choice is the completion of the extension
$\Omega ,$
i.e., the minimal choice is the completion of the extension
![]() $L_\infty (\Omega )$
of
$L_\infty (\Omega )$
of
![]() $L_\infty $
; by an observation of Colmez the completion
$L_\infty $
; by an observation of Colmez the completion
![]() $\widehat {L^{ab}}$
would be a possible choice, where we write
$\widehat {L^{ab}}$
would be a possible choice, where we write
![]() $L^{ab}=L^{nr}L_\infty $
and
$L^{ab}=L^{nr}L_\infty $
and
![]() $L^{nr}$
for the maximal abelian and for the maximal unramified extension of L, respectively. If
$L^{nr}$
for the maximal abelian and for the maximal unramified extension of L, respectively. If
![]() $L\neq {\Bbb Q}_p$
, such K cannot be discretely valued even if we replace
$L\neq {\Bbb Q}_p$
, such K cannot be discretely valued even if we replace
![]() $L_\infty $
by
$L_\infty $
by
![]() $L,$
see [Reference Schneider and Teitelbaum42, Lem. 3.9]. Following Colmez we define
$L,$
see [Reference Schneider and Teitelbaum42, Lem. 3.9]. Following Colmez we define
![]() $K_n:=L_n\otimes _LK=\prod _{(o_L/\pi _L^n)^\times }K,$
where the latter identification is given by mapping
$K_n:=L_n\otimes _LK=\prod _{(o_L/\pi _L^n)^\times }K,$
where the latter identification is given by mapping
![]() $l\otimes _L k$
to
$l\otimes _L k$
to
![]() $(\sigma _a(l)\cdot k)_{a\in (o_L/\pi _L^n)^\times }$
, and have the maps
$(\sigma _a(l)\cdot k)_{a\in (o_L/\pi _L^n)^\times }$
, and have the maps
 $$\begin{align*}\mathrm{Tr}_{K_n/K}:\prod_{(o_L/\pi_L^n)^\times}K\to K,\; (l_a)_{a\in (o_L/\pi_L^n)^\times }\mapsto \sum_{a\in (o_L/\pi_L^n)^\times } l_a.\end{align*}$$
$$\begin{align*}\mathrm{Tr}_{K_n/K}:\prod_{(o_L/\pi_L^n)^\times}K\to K,\; (l_a)_{a\in (o_L/\pi_L^n)^\times }\mapsto \sum_{a\in (o_L/\pi_L^n)^\times } l_a.\end{align*}$$
Note that we have
![]() $v_p(\Omega )=\frac {1}{p-1}-\frac {1}{e(q-1)}$
and, for
$v_p(\Omega )=\frac {1}{p-1}-\frac {1}{e(q-1)}$
and, for
![]() $n\geq 1, r_n:=v_p(u_n)=\frac {1}{e(q-1)q^{n-1}}$
.
$n\geq 1, r_n:=v_p(u_n)=\frac {1}{e(q-1)q^{n-1}}$
.
For any ring R, let
![]() $\mathbf {D}^{[a,b]}_{\mathrm {perf}}(R)$
(respectively
$\mathbf {D}^{[a,b]}_{\mathrm {perf}}(R)$
(respectively
![]() $\mathbf {D}^b_{\mathrm {perf}}(R)$
,
$\mathbf {D}^b_{\mathrm {perf}}(R)$
,
![]() $\mathbf {D}^-_{\mathrm {perf}}(R)$
) denote the triangulated subcategory of the derived category
$\mathbf {D}^-_{\mathrm {perf}}(R)$
) denote the triangulated subcategory of the derived category
![]() $\mathbf {D}(R)$
of (cochain) complexes of R-modules consisting of the complexes of R-modules which are quasi-isomorphic to complexes of finitely generated projective R-modules concentrated in degrees
$\mathbf {D}(R)$
of (cochain) complexes of R-modules consisting of the complexes of R-modules which are quasi-isomorphic to complexes of finitely generated projective R-modules concentrated in degrees
![]() $[a,b]$
(respectively bounded degrees, degrees bounded above).
$[a,b]$
(respectively bounded degrees, degrees bounded above).
Furthermore, if R is a commutative ring, X an R-module and
![]() $t\in R$
a non-zerodivisor, we write
$t\in R$
a non-zerodivisor, we write
![]() $X_{t} :=X[\frac {1}{t}]$
for the localisation at the multiplicatively closed set
$X_{t} :=X[\frac {1}{t}]$
for the localisation at the multiplicatively closed set
![]() $\{1,t,t^2,\ldots \}$
.
$\{1,t,t^2,\ldots \}$
.
For a locally L-analytic group G and a complete field
![]() $F\subseteq \mathbb {C}_p$
containing L we write
$F\subseteq \mathbb {C}_p$
containing L we write
![]() $D(G,F)$
for the locally L-analytic distribution algebra with coefficients in F; if the coefficients are clear from the context we often abbreviate this as
$D(G,F)$
for the locally L-analytic distribution algebra with coefficients in F; if the coefficients are clear from the context we often abbreviate this as
![]() $D(G)$
. Dirac distributions associated with group elements
$D(G)$
. Dirac distributions associated with group elements
![]() $g\in G$
are denoted by
$g\in G$
are denoted by
![]() $\delta _g$
or
$\delta _g$
or
![]() $[g]$
.
$[g]$
.
3
 $(\varphi _L,\Gamma _L)$
-Modules over the Robba ring
$(\varphi _L,\Gamma _L)$
-Modules over the Robba ring
For the entire section, fix a complete intermediate field F of the extension
![]() $\mathbb {C}_p/L.$
$\mathbb {C}_p/L.$
3.1 Definition of the Robba ring
 $\mathcal {R}$
$\mathcal {R}$
For any interval
![]() $I\subseteq (0,\infty )$
that is either compact or of the form
$I\subseteq (0,\infty )$
that is either compact or of the form
![]() $(0,r]$
,
$(0,r]$
,
![]() $r>0$
, we define
$r>0$
, we define
 $$ \begin{align*} \mathcal{R}^{I}_F:=\left\{\sum_{k\in \mathbb{Z}}a_k\cdot Z^k\mid a_k\in F,\ \lim_{\lvert k \rvert \to\infty}v_{F}(a_k)+kt=\infty\text{ for all }t\in I \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{R}^{I}_F:=\left\{\sum_{k\in \mathbb{Z}}a_k\cdot Z^k\mid a_k\in F,\ \lim_{\lvert k \rvert \to\infty}v_{F}(a_k)+kt=\infty\text{ for all }t\in I \right\}. \end{align*} $$
We always assume that the boundary points of I are in the value group of
![]() $v_F$
, so that
$v_F$
, so that
![]() $\mathcal {R}_F^I$
is the ring of rigid analytic functions on the annulus
$\mathcal {R}_F^I$
is the ring of rigid analytic functions on the annulus
Furthermore, for
![]() $r>0$
, let
$r>0$
, let
i.e. the ring of rigid analytic functions on the annulus with outer radius
![]() $1$
and inner radius depending on r. For any
$1$
and inner radius depending on r. For any
![]() $s\in (0,r]$
, one has
$s\in (0,r]$
, one has
![]() $\mathcal {R}_F^{[s,r]}\subseteq \mathcal {R}_F^r$
, and
$\mathcal {R}_F^{[s,r]}\subseteq \mathcal {R}_F^r$
, and
![]() $\mathcal {R}_F^{[s,r]}$
is a Banach algebra over F with the norm
$\mathcal {R}_F^{[s,r]}$
is a Banach algebra over F with the norm
 $$ \begin{align*} V_{[s,r]}\left(f \right)=\min_{t\in [s,r]}\left(\inf_{k\in\mathbb{Z}} (v_F(a_k)+kt)\right),\ \ \ \text{ where }f=\sum_{k\in\mathbb{Z}}a_k Z^k\in \mathcal{R}_F^{[s,r]}. \end{align*} $$
$$ \begin{align*} V_{[s,r]}\left(f \right)=\min_{t\in [s,r]}\left(\inf_{k\in\mathbb{Z}} (v_F(a_k)+kt)\right),\ \ \ \text{ where }f=\sum_{k\in\mathbb{Z}}a_k Z^k\in \mathcal{R}_F^{[s,r]}. \end{align*} $$
Thus
![]() $\mathcal {R}_F^r=\bigcap _{0<s\leq r}\mathcal {R}_F^{[s,r]}$
is a Fréchet space. There are natural inclusions
$\mathcal {R}_F^r=\bigcap _{0<s\leq r}\mathcal {R}_F^{[s,r]}$
is a Fréchet space. There are natural inclusions
![]() $\mathcal {R}_F^r\subseteq \mathcal {R}_F^s$
for
$\mathcal {R}_F^r\subseteq \mathcal {R}_F^s$
for
![]() $s\leq r$
. Now the Robba ring over F in the variable Z is defined by
$s\leq r$
. Now the Robba ring over F in the variable Z is defined by
We endow
![]() $\mathcal {R}_F$
with the locally convex direct limit topology of the
$\mathcal {R}_F$
with the locally convex direct limit topology of the
![]() $\mathcal {R}_F^r$
, making it an LF-space.
$\mathcal {R}_F^r$
, making it an LF-space.
Moreover, let
This is the ring of power series with coefficients in F that are convergent on the open unit disk. In particular, we have
![]() $\mathcal {R}_F^+\subseteq \mathcal {R}_F^r$
for all
$\mathcal {R}_F^+\subseteq \mathcal {R}_F^r$
for all
![]() $r>0$
. For a complete field extension
$r>0$
. For a complete field extension
![]() $F\subset F' \subset \mathbb {C}_p$
we have
$F\subset F' \subset \mathbb {C}_p$
we have
(see. [Reference Berger, Schneider and Xie7, Corollary 2.1.8]). Their proof also shows
![]() $F' \hat {\otimes }_{F,\pi }\mathcal {R}_F^{r}\cong \mathcal {R}_{F'}^r.$
$F' \hat {\otimes }_{F,\pi }\mathcal {R}_F^{r}\cong \mathcal {R}_{F'}^r.$
Inside
![]() $\mathcal {R}_F$
, we have the subring
$\mathcal {R}_F$
, we have the subring
![]() $\mathcal {R}_F^b$
of bounded elements, i.e., those Laurent series
$\mathcal {R}_F^b$
of bounded elements, i.e., those Laurent series
![]() $f=\sum _{k\in \mathbb {Z}}a_k Z^k$
where the coefficients
$f=\sum _{k\in \mathbb {Z}}a_k Z^k$
where the coefficients
![]() $a_k$
are bounded in F. It is well-known that
$a_k$
are bounded in F. It is well-known that
![]() $\mathcal {R}_F^\times =(\mathcal {R}_F^b)^\times $
. Furthermore, the map
$\mathcal {R}_F^\times =(\mathcal {R}_F^b)^\times $
. Furthermore, the map
![]() $f\mapsto \lVert f\rVert _1:=\sup _k\lvert a_k\rvert $
defines a multiplicative norm on
$f\mapsto \lVert f\rVert _1:=\sup _k\lvert a_k\rvert $
defines a multiplicative norm on
![]() $\mathcal {R}_F^b$
, see [Reference Berger, Schneider and Xie7, §1.3].
$\mathcal {R}_F^b$
, see [Reference Berger, Schneider and Xie7, §1.3].
3.2 Frobenius and
 $\Gamma _L$
-action on
$\Gamma _L$
-action on
 $\mathcal {R}$
$\mathcal {R}$
On
![]() $\mathcal {R}_F$
, we define a Frobenius
$\mathcal {R}_F$
, we define a Frobenius
![]() $\varphi _L$
and a commuting
$\varphi _L$
and a commuting
![]() $\Gamma _L$
-action by
$\Gamma _L$
-action by
on the variable and trivial actions on the coefficients. For
![]() $r>0$
, the Frobenius
$r>0$
, the Frobenius
![]() $\varphi _L$
and each
$\varphi _L$
and each
![]() $\gamma \in \Gamma _L$
restrict to maps
$\gamma \in \Gamma _L$
restrict to maps
For r small enough, there is a left inverse
of
![]() $\varphi _L$
, given by
$\varphi _L$
, given by
![]() $\Psi =\frac {\varphi _L^{-1}}{q}\circ \operatorname {\mathrm {Tr}}_{\mathcal {R}_F^{r/q}/\varphi _L(\mathcal {R}_F^r)}$
, see [Reference Fourquaux and Xie22, §2]. We have
$\Psi =\frac {\varphi _L^{-1}}{q}\circ \operatorname {\mathrm {Tr}}_{\mathcal {R}_F^{r/q}/\varphi _L(\mathcal {R}_F^r)}$
, see [Reference Fourquaux and Xie22, §2]. We have
![]() $\Psi = \frac {\pi _L}{q}\psi _L.$
$\Psi = \frac {\pi _L}{q}\psi _L.$
3.3
 $(\varphi _L,\Gamma _L)$
-Modules
$(\varphi _L,\Gamma _L)$
-Modules
Definition 3.1. A
![]() $\varphi _L$
-module over
$\varphi _L$
-module over
![]() $\mathcal {R}_F$
is a finitely generated free
$\mathcal {R}_F$
is a finitely generated free
![]() $\mathcal {R}_F$
-module M, equipped with a continuousFootnote
3
,
$\mathcal {R}_F$
-module M, equipped with a continuousFootnote
3
,
![]() $\varphi _L$
-semilinear endomorphism
$\varphi _L$
-semilinear endomorphism
![]() $\varphi _M$
, such that the induced
$\varphi _M$
, such that the induced
![]() $\mathcal {R}_F$
-linear map
$\mathcal {R}_F$
-linear map
is an isomorphism. Note that in the above tensor product,
![]() $\mathcal {R}_F$
is viewed as a left-module over itself in the usual way and as a right module via
$\mathcal {R}_F$
is viewed as a left-module over itself in the usual way and as a right module via
![]() $ \varphi _L$
.
$ \varphi _L$
.
We will often simply write
![]() $\varphi $
instead of
$\varphi $
instead of
![]() $\varphi _M$
.
$\varphi _M$
.
Proposition 3.2. Let M be a
![]() $\varphi _L$
-module over
$\varphi _L$
-module over
![]() $\mathcal {R}_F$
. Then there exists an
$\mathcal {R}_F$
. Then there exists an
![]() $r(M)>0$
such that, for each
$r(M)>0$
such that, for each
![]() $0<r\leq r(M)$
, there exists a unique finitely generated free
$0<r\leq r(M)$
, there exists a unique finitely generated free
![]() $\mathcal {R}_F^r$
-submodule
$\mathcal {R}_F^r$
-submodule
![]() $M^r\subseteq M$
satisfying the following properties:
$M^r\subseteq M$
satisfying the following properties:
-
(i)
 $M=\mathcal {R}_F\otimes _{\mathcal {R}_F^r}M^r$
.
$M=\mathcal {R}_F\otimes _{\mathcal {R}_F^r}M^r$
. -
(ii)
 $\varphi _M$
induces an isomorphism
$\varphi _M$
induces an isomorphism
 $\mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r,\varphi _L}M^r\overset {\sim }{\longrightarrow } \mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r}M^r$
.
$\mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r,\varphi _L}M^r\overset {\sim }{\longrightarrow } \mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r}M^r$
.
In particular, for
![]() $0<s\leq r\leq r(M)$
, one has
$0<s\leq r\leq r(M)$
, one has
Proof. See Thm. I.3.3 in [Reference Berger4].
Remark 3.3. Let M be a
![]() $\varphi _L$
-module over
$\varphi _L$
-module over
![]() $\mathcal {R}_F$
. Then for
$\mathcal {R}_F$
. Then for
![]() $0<s\leq r \leq r(M)$
and
$0<s\leq r \leq r(M)$
and
![]() ${?\in \{s,[s,r],\varnothing \}}$
we write
${?\in \{s,[s,r],\varnothing \}}$
we write
Composing the canonical map
![]() $M^r\longrightarrow \mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r,\varphi _L}M^r,\ m\longmapsto 1\otimes m$
with the isomorphism
$M^r\longrightarrow \mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r,\varphi _L}M^r,\ m\longmapsto 1\otimes m$
with the isomorphism
![]() $\mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r,\varphi _L}M^r\cong M^{r/q}$
from Prop. 3.2(ii) above, we obtain
$\mathcal {R}_F^{r/q}\otimes _{\mathcal {R}_F^r,\varphi _L}M^r\cong M^{r/q}$
from Prop. 3.2(ii) above, we obtain
![]() $\varphi _L$
-semilinear maps
$\varphi _L$
-semilinear maps
There is also an operator
given by
![]() $f\otimes m\longmapsto \Psi (f)\cdot m$
.
$f\otimes m\longmapsto \Psi (f)\cdot m$
.
Definition 3.4. A
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_F$
is a
$\mathcal {R}_F$
is a
![]() $\varphi _L$
-module M over
$\varphi _L$
-module M over
![]() $\mathcal {R}_F$
which carries a continuous, semilinear action of
$\mathcal {R}_F$
which carries a continuous, semilinear action of
![]() $\Gamma _L$
that commutes with
$\Gamma _L$
that commutes with
![]() $\varphi _M$
. We shall write
$\varphi _M$
. We shall write
![]() $\mathfrak {M}(\mathcal {R}_F)$
for the category of
$\mathfrak {M}(\mathcal {R}_F)$
for the category of
![]() $(\varphi _L,\Gamma _L)$
-modules over
$(\varphi _L,\Gamma _L)$
-modules over
![]() $\mathcal {R}_F.$
$\mathcal {R}_F.$
Remark 3.5. If M is a
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_F$
and
$\mathcal {R}_F$
and
![]() $0<r\leq r(M)$
, then from the uniqueness in Prop. 3.2 it follows that
$0<r\leq r(M)$
, then from the uniqueness in Prop. 3.2 it follows that
![]() $\gamma (M^r)=M^r$
for all
$\gamma (M^r)=M^r$
for all
![]() $\gamma \in \Gamma _L$
.
$\gamma \in \Gamma _L$
.
Definition 3.6.
-
(i) For
 $n\geq 1$
we put
$n\geq 1$
we put
 $r_n:=v_p(u_n)=\frac {1}{e(q-1)q^{n-1}}$
.
$r_n:=v_p(u_n)=\frac {1}{e(q-1)q^{n-1}}$
. -
(ii) Let M be a
 $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
 $\mathcal {R}_F$
. For any n such that
$\mathcal {R}_F$
. For any n such that
 $r_n\leq r(M)$
, define
$r_n\leq r(M)$
, define  $$ \begin{align*} M^{(n)}:=M^{r_n}. \end{align*} $$
$$ \begin{align*} M^{(n)}:=M^{r_n}. \end{align*} $$
Observe that for the Frobenius we then have
 $\varphi \colon M^{(n)} \longrightarrow M^{(n+1)}$
for
$\varphi \colon M^{(n)} \longrightarrow M^{(n+1)}$
for
 $n\gg 0$
.
$n\gg 0$
.
Let M be a
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_F$
. After fixing a basis of M, consider the matrix
$\mathcal {R}_F$
. After fixing a basis of M, consider the matrix
![]() $P\in \operatorname {GL}_n(\mathcal {R}_F)$
representing
$P\in \operatorname {GL}_n(\mathcal {R}_F)$
representing
![]() $\varphi _M$
. Then we have
$\varphi _M$
. Then we have
![]() $\det (P)\in \mathcal {R}_F^\times =(\mathcal {R}_F^b)^\times $
and may thus take the norm
$\det (P)\in \mathcal {R}_F^\times =(\mathcal {R}_F^b)^\times $
and may thus take the norm
![]() $\lVert \det (P) \rVert _1$
introduced at the end of Subsection 3.1. Define the degree
$\lVert \det (P) \rVert _1$
introduced at the end of Subsection 3.1. Define the degree
![]() $\deg (M)$
of M as the number satisfying
$\deg (M)$
of M as the number satisfying
![]() $\lVert \det (P)\rVert _1=q^{-\deg (M)}$
; one checks that this is independent of the initial choice of basis of M, see [Reference Berger, Schneider and Xie7, §3.3] for details. Furthermore, the slope of M is defined as
$\lVert \det (P)\rVert _1=q^{-\deg (M)}$
; one checks that this is independent of the initial choice of basis of M, see [Reference Berger, Schneider and Xie7, §3.3] for details. Furthermore, the slope of M is defined as
![]() $\mu (M):=\deg (M)/\operatorname {rk}(M)$
.
$\mu (M):=\deg (M)/\operatorname {rk}(M)$
.
Definition 3.7. A
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_F$
is called étale, if it has degree
$\mathcal {R}_F$
is called étale, if it has degree
![]() $0$
and every
$0$
and every
![]() $(\varphi _L,\Gamma _L)$
-submodule has slope
$(\varphi _L,\Gamma _L)$
-submodule has slope
![]() $\geq 0$
.
$\geq 0$
.
Definition 3.8. For an affinoid algebra A over F we define
![]() $\mathcal {R}_A^I:= A \hat {\otimes }_F\mathcal {R}_F^I$
(with the projective tensor product topology) and similarly
$\mathcal {R}_A^I:= A \hat {\otimes }_F\mathcal {R}_F^I$
(with the projective tensor product topology) and similarly
![]() $\mathcal {R}_A^r$
and
$\mathcal {R}_A^r$
and
![]() $\mathcal {R}_A.$
We can extend A-linearly the actions of
$\mathcal {R}_A.$
We can extend A-linearly the actions of
![]() $\varphi _L$
and
$\varphi _L$
and
![]() $\Gamma _L.$
By a
$\Gamma _L.$
By a
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_A$
we mean a
$\mathcal {R}_A$
we mean a
![]() $\mathcal {R}_A$
-module M which arises as a base change of a projective
$\mathcal {R}_A$
-module M which arises as a base change of a projective
![]() $\mathcal {R}_A^r$
-module
$\mathcal {R}_A^r$
-module
![]() $M^r$
for some
$M^r$
for some
![]() $r \gg 0,$
together with a continuous
$r \gg 0,$
together with a continuous
![]() $\mathcal {R}_A^r$
-semilinear action of
$\mathcal {R}_A^r$
-semilinear action of
![]() $\Gamma _L$
on
$\Gamma _L$
on
![]() $M^r$
and a
$M^r$
and a
![]() $\varphi _L$
-semilinear map
$\varphi _L$
-semilinear map
![]() $\varphi _M \colon M^r \to M^{r/q},$
which commutes with
$\varphi _M \colon M^r \to M^{r/q},$
which commutes with
![]() $\Gamma _L.$
We can analogously extend the definition of
$\Gamma _L.$
We can analogously extend the definition of
![]() $\Psi .$
$\Psi .$
If F is not spherically complete, we do not know if there exist non-free, projective
![]() $(\varphi _L,\Gamma _L)$
-modules over
$(\varphi _L,\Gamma _L)$
-modules over
![]() $\mathcal {R}_F.$
In all cases considered by us, we will only need free modules. According to [Reference Berger, Schneider and Xie7] Prop. 2.25 the
$\mathcal {R}_F.$
In all cases considered by us, we will only need free modules. According to [Reference Berger, Schneider and Xie7] Prop. 2.25 the
![]() $\Gamma _L$
-action on a
$\Gamma _L$
-action on a
![]() $(\varphi _L,\Gamma _L)$
-module M is differentiable so that the derived action of the Lie algebra
$(\varphi _L,\Gamma _L)$
-module M is differentiable so that the derived action of the Lie algebra
![]() $\operatorname {Lie}(o_L^\times )$
on M is available.
$\operatorname {Lie}(o_L^\times )$
on M is available.
Definition 3.9. A
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R} \in \{\mathcal {R}_F,\mathcal {R}_A\}$
is called L-analytic, if the derived action
$\mathcal {R} \in \{\mathcal {R}_F,\mathcal {R}_A\}$
is called L-analytic, if the derived action
![]() $\operatorname {Lie}(\Gamma _L) \times M \rightarrow M$
is L-bilinear, i.e., if the induced action
$\operatorname {Lie}(\Gamma _L) \times M \rightarrow M$
is L-bilinear, i.e., if the induced action
![]() $\operatorname {Lie}(\Gamma _L)\to \operatorname {End}(M)$
of the Lie algebra
$\operatorname {Lie}(\Gamma _L)\to \operatorname {End}(M)$
of the Lie algebra
![]() $\operatorname {Lie}(\Gamma _L)$
of
$\operatorname {Lie}(\Gamma _L)$
of
![]() $\Gamma _L$
is L-linear (and not just
$\Gamma _L$
is L-linear (and not just
![]() $\mathbb {Q}_p$
-linear). We shall write
$\mathbb {Q}_p$
-linear). We shall write
![]() $\mathfrak {M}^{an}(\mathcal {R})$
for the category of L-analytic
$\mathfrak {M}^{an}(\mathcal {R})$
for the category of L-analytic
![]() $(\varphi _L,\Gamma _L)$
-modules over
$(\varphi _L,\Gamma _L)$
-modules over
![]() $\mathcal {R}.$
$\mathcal {R}.$
In the case
![]() $\mathcal {R}=\mathcal {R}_F$
, we write
$\mathcal {R}=\mathcal {R}_F$
, we write
![]() $\mathfrak {M}^{an,\acute {e}t}(\mathcal {R}_F)$
for the category of étale, L-analytic
$\mathfrak {M}^{an,\acute {e}t}(\mathcal {R}_F)$
for the category of étale, L-analytic
![]() $(\varphi _L,\Gamma _L)$
-modules over
$(\varphi _L,\Gamma _L)$
-modules over
![]() $\mathcal {R}_F.$
$\mathcal {R}_F.$
For the relation with L-analytic continuous Galois representations
![]() $Rep_L^{an}(G_L)$
of
$Rep_L^{an}(G_L)$
of
![]() $G_L$
on finite dimensional vector spaces V, which are analytic, i.e., satisfying that, if
$G_L$
on finite dimensional vector spaces V, which are analytic, i.e., satisfying that, if
![]() $D_{dR}^{\mathbb {Q}_p}(V) := (V \otimes _{\mathbb {Q}_p} B_{dR})^{G_L}$
, the filtration on
$D_{dR}^{\mathbb {Q}_p}(V) := (V \otimes _{\mathbb {Q}_p} B_{dR})^{G_L}$
, the filtration on
![]() $D_{dR}^{\mathbb {Q}_p}(V)_{\mathfrak {m}}$
is trivial for each maximal ideal
$D_{dR}^{\mathbb {Q}_p}(V)_{\mathfrak {m}}$
is trivial for each maximal ideal
![]() $\mathfrak {m}$
of
$\mathfrak {m}$
of
![]() $L \otimes _{\mathbb {Q}_p} L$
which does not correspond to the identity
$L \otimes _{\mathbb {Q}_p} L$
which does not correspond to the identity
![]() $\operatorname {id} : L \to L$
, Berger’s theorem is crucial.
$\operatorname {id} : L \to L$
, Berger’s theorem is crucial.
Theorem 3.10. There is an equivalences of categories
 $$ \begin{align*} Rep_L^{an}(G_L) & \longleftrightarrow \mathfrak{M}^{an,\acute{e}t}(\mathcal{R}_L) \\ V & \mapsto D_{\mathrm{rig}}^\dagger(V). \end{align*} $$
$$ \begin{align*} Rep_L^{an}(G_L) & \longleftrightarrow \mathfrak{M}^{an,\acute{e}t}(\mathcal{R}_L) \\ V & \mapsto D_{\mathrm{rig}}^\dagger(V). \end{align*} $$
Proof. Thm. D in [Reference Berger5]
The embedding ![]() in (5) depends by construction on the choice of u. Any other choice does not change the image of the embedding
in (5) depends by construction on the choice of u. Any other choice does not change the image of the embedding ![]() because
because
![]() $Z_{au} = [a](Z_u)$
for
$Z_{au} = [a](Z_u)$
for
![]() $a \in o_L^\times $
by property (i) above (5). As explained in [Reference Schneider and Venjakob47, §8] the image
$a \in o_L^\times $
by property (i) above (5). As explained in [Reference Schneider and Venjakob47, §8] the image
![]() $Z_u$
of the variable Z already lies in
$Z_u$
of the variable Z already lies in
![]() $W({\hat {L}_\infty }^\flat )_L$
, so that we actually have an embedding
$W({\hat {L}_\infty }^\flat )_L$
, so that we actually have an embedding
![]() $o_L[[Z]]\to W({\hat {L}_\infty }^\flat )_L$
. Similarly, as in [Reference Kedlaya and Liu29, Def. 4.3.1] for the cyclotomic situation one shows that the latter embedding extends to a
$o_L[[Z]]\to W({\hat {L}_\infty }^\flat )_L$
. Similarly, as in [Reference Kedlaya and Liu29, Def. 4.3.1] for the cyclotomic situation one shows that the latter embedding extends to a
![]() $\Gamma _L$
- and
$\Gamma _L$
- and
![]() $\varphi _L$
-equivariant topological monomorphism
$\varphi _L$
-equivariant topological monomorphism
![]() $\mathcal {R}_L\to \tilde {\mathcal {R}}_L$
into the perfect Robba ring, see [Reference Schneider and Venjakob47, §5] for a definition and [Reference Witzelsperger57, Konstruktion 1.3.27] for a proof in the Lubin-Tate setting.
$\mathcal {R}_L\to \tilde {\mathcal {R}}_L$
into the perfect Robba ring, see [Reference Schneider and Venjakob47, §5] for a definition and [Reference Witzelsperger57, Konstruktion 1.3.27] for a proof in the Lubin-Tate setting.
Remark 3.11. In order to trace the choice of u in our constructions, we should view
![]() $\mathcal {R}_L$
as a subring of
$\mathcal {R}_L$
as a subring of
![]() $\widetilde {\mathcal {R}}_L$
via the embedding induced by
$\widetilde {\mathcal {R}}_L$
via the embedding induced by
![]() $Z \mapsto Z_u$
and define
$Z \mapsto Z_u$
and define
![]() $(\varphi _L,\Gamma _L)$
-modules over this (isomorphic) subring. We will ignore this dependence for the most part by working with a fixed
$(\varphi _L,\Gamma _L)$
-modules over this (isomorphic) subring. We will ignore this dependence for the most part by working with a fixed
![]() $Z = Z_u.$
This “hidden” dependence on u is only relevant if an element of a
$Z = Z_u.$
This “hidden” dependence on u is only relevant if an element of a
![]() $(\varphi _L,\Gamma _L)$
-module is explicitly defined in terms of power series in the variable Z, see e.g. (77), (79), (30).
$(\varphi _L,\Gamma _L)$
-module is explicitly defined in terms of power series in the variable Z, see e.g. (77), (79), (30).
3.4 Rank one modules and characters
Let A be an affinoid algebra over
![]() $F.$
To each continuous character
$F.$
To each continuous character
![]() $\delta \colon L^\times \to A^\times $
we can attach a
$\delta \colon L^\times \to A^\times $
we can attach a
![]() $(\varphi _L,\Gamma _L)$
-module of rank one
$(\varphi _L,\Gamma _L)$
-module of rank one
![]() $\mathcal {R}_A(\delta ) := \mathcal {R}_A\mathbf {e}_\delta $
by setting
$\mathcal {R}_A(\delta ) := \mathcal {R}_A\mathbf {e}_\delta $
by setting
![]() $\varphi _L(\mathbf {e}_\delta ) = \delta (\pi _L)\mathbf {e}_\delta $
and
$\varphi _L(\mathbf {e}_\delta ) = \delta (\pi _L)\mathbf {e}_\delta $
and
![]() $\gamma (\mathbf {e}_\delta ) = \delta (\chi _{LT}(\gamma ))\mathbf {e}_\delta $
for
$\gamma (\mathbf {e}_\delta ) = \delta (\chi _{LT}(\gamma ))\mathbf {e}_\delta $
for
![]() $\gamma \in \Gamma _L.$
We say a module is of character type if it arises in this way. A
$\gamma \in \Gamma _L.$
We say a module is of character type if it arises in this way. A
![]() $(\varphi _L,\Gamma _L)$
-module of character type is L-analytic (in the sense of Definition 3.9) if and only if
$(\varphi _L,\Gamma _L)$
-module of character type is L-analytic (in the sense of Definition 3.9) if and only if
![]() $\delta $
is locally L-analytic (or equivalently
$\delta $
is locally L-analytic (or equivalently
![]() $\delta _{|o_L^\times }$
is locally L-analytic). Over
$\delta _{|o_L^\times }$
is locally L-analytic). Over
![]() $\mathcal {R}_L$
any rank one module is of character type (cf. [Reference Fourquaux and Xie22, Proposition 1.9]). We write
$\mathcal {R}_L$
any rank one module is of character type (cf. [Reference Fourquaux and Xie22, Proposition 1.9]). We write
![]() ${\Sigma =\Sigma (A)}$
for the set of continuous characters
${\Sigma =\Sigma (A)}$
for the set of continuous characters
![]() $\delta :L^\times \to A^\times $
. We denote by
$\delta :L^\times \to A^\times $
. We denote by
![]() $\Sigma _{an}:=\Sigma _{an}(A)$
the set of locally L-analytic characters
$\Sigma _{an}:=\Sigma _{an}(A)$
the set of locally L-analytic characters
![]() $\delta \colon L ^\times \to A^\times $
. Consider the following characters
$\delta \colon L ^\times \to A^\times $
. Consider the following characters
![]() $\delta _{LT},\chi =x|x|, \delta ^{un}_c:L^\times \to L^\times $
for
$\delta _{LT},\chi =x|x|, \delta ^{un}_c:L^\times \to L^\times $
for
![]() $c\in L^\times $
given by
$c\in L^\times $
given by
 $$ \begin{align*} \delta_{LT}(\pi_L)=1, &\; \delta_{LT|o_L^\times}=\operatorname{id} _{o_L^\times}, \\ \chi(\pi_L)=\frac{\pi_L}{q} ,&\; \chi_{|o_L^\times}=\operatorname{id} _{o_L^\times}, \\ \delta^{un}_c(\pi_L)=c, & \; (\delta^{un}_c)_{|o_L^\times}\equiv1. \end{align*} $$
$$ \begin{align*} \delta_{LT}(\pi_L)=1, &\; \delta_{LT|o_L^\times}=\operatorname{id} _{o_L^\times}, \\ \chi(\pi_L)=\frac{\pi_L}{q} ,&\; \chi_{|o_L^\times}=\operatorname{id} _{o_L^\times}, \\ \delta^{un}_c(\pi_L)=c, & \; (\delta^{un}_c)_{|o_L^\times}\equiv1. \end{align*} $$
In particular,
![]() $\chi =\delta ^{un}_{\frac {\pi _L}{q}}\delta _{LT}.$
Then
$\chi =\delta ^{un}_{\frac {\pi _L}{q}}\delta _{LT}.$
Then
![]() $\delta _{LT}$
corresponds via class field theory to the character
$\delta _{LT}$
corresponds via class field theory to the character
![]() $\chi _{LT}\colon G_L\to o_L^\times .$
Let
$\chi _{LT}\colon G_L\to o_L^\times .$
Let
![]() $\delta \colon L^\times \to L^\times $
be any continuous character; setting
$\delta \colon L^\times \to L^\times $
be any continuous character; setting
![]() $\delta _0:=\delta ^{un}_{\delta ^{-1}(\pi _L)}\delta $
we may always decompose
$\delta _0:=\delta ^{un}_{\delta ^{-1}(\pi _L)}\delta $
we may always decompose
![]() $\delta = \delta ^{un}_{\delta (\pi _L)}\delta _0$
satisfying
$\delta = \delta ^{un}_{\delta (\pi _L)}\delta _0$
satisfying
![]() $\delta _{|o_L^\times } = (\delta _0)_{|o_L^\times }$
and
$\delta _{|o_L^\times } = (\delta _0)_{|o_L^\times }$
and
![]() $\delta _0(\pi _L)=1.$
If
$\delta _0(\pi _L)=1.$
If
![]() $|\delta (\pi _L)|=1$
, the character
$|\delta (\pi _L)|=1$
, the character
![]() $\delta $
corresponds to a Galois character
$\delta $
corresponds to a Galois character
![]() $\chi _\delta $
via local class field theory. Then
$\chi _\delta $
via local class field theory. Then
![]() $D^\dagger _{rig}(L(\chi _\delta ))=\mathcal {R}_L(\delta )$
and we call
$D^\dagger _{rig}(L(\chi _\delta ))=\mathcal {R}_L(\delta )$
and we call
![]() $\delta $
étale.
$\delta $
étale.
Later, for descent calculations we will have to select out the sets of special characters
![]() $\Sigma _1:=\{x^{-i}| i\in \mathbb {N}\}$
and
$\Sigma _1:=\{x^{-i}| i\in \mathbb {N}\}$
and
![]() $\Sigma _2:=\{x^{i}\chi | i\in \mathbb {N}\}$
from the generic ones
$\Sigma _2:=\{x^{i}\chi | i\in \mathbb {N}\}$
from the generic ones
![]() $\Sigma _{gen}:=\Sigma _{an}\setminus (\Sigma _1\cup \Sigma _2).$
$\Sigma _{gen}:=\Sigma _{an}\setminus (\Sigma _1\cup \Sigma _2).$
Note that we have two
![]() $\psi $
-operators. While
$\psi $
-operators. While
![]() $\psi $
satisfies the identity
$\psi $
satisfies the identity
![]() $\psi \circ \varphi =\frac {q}{\pi _L}\operatorname {id}$
and makes sense even integrally,
$\psi \circ \varphi =\frac {q}{\pi _L}\operatorname {id}$
and makes sense even integrally,
![]() $\Psi $
denotes the left inverse of
$\Psi $
denotes the left inverse of
![]() $\varphi ,$
i.e., satisfying
$\varphi ,$
i.e., satisfying
![]() $\Psi \circ \varphi = \operatorname {id}$
. In particular, we have
$\Psi \circ \varphi = \operatorname {id}$
. In particular, we have
![]() $\psi =\frac {q}{\pi _L}\Psi .$
Note that
$\psi =\frac {q}{\pi _L}\Psi .$
Note that
![]() $\psi (\mathbf {e}_\delta )=\frac {q}{\pi _L}\delta ^{-1}(\pi _L)\mathbf {e}_\delta .$
$\psi (\mathbf {e}_\delta )=\frac {q}{\pi _L}\delta ^{-1}(\pi _L)\mathbf {e}_\delta .$
If
![]() $\delta \in \Sigma _{an}(K)$
and
$\delta \in \Sigma _{an}(K)$
and
![]() $a \in o_L^\times $
such that
$a \in o_L^\times $
such that
![]() $\log (a) \neq 0,$
then one defines the weight of
$\log (a) \neq 0,$
then one defines the weight of
![]() $\delta $
as
$\delta $
as
![]() $\omega _\delta := \log (\delta (a))/\log (a)$
(which is independent of a). We shall say that
$\omega _\delta := \log (\delta (a))/\log (a)$
(which is independent of a). We shall say that
![]() $\delta $
is de Rham, if the attached
$\delta $
is de Rham, if the attached
![]() $(\varphi _L,\Gamma _L)$
-module
$(\varphi _L,\Gamma _L)$
-module
![]() $R_K(\delta )$
is de Rham in the sense that will be introduced in subsection 5.4 below. As shown in the Appendix A, Remark A.8,
$R_K(\delta )$
is de Rham in the sense that will be introduced in subsection 5.4 below. As shown in the Appendix A, Remark A.8,
![]() $\delta $
is de Rham if and only if there exist some locally constant character
$\delta $
is de Rham if and only if there exist some locally constant character
![]() $\delta _{\mathrm {lc}}$
and
$\delta _{\mathrm {lc}}$
and
![]() $k(=\omega _\delta )\in \mathbb {Z,}$
such that
$k(=\omega _\delta )\in \mathbb {Z,}$
such that
see also [Reference Schneider and Venjakob46, Rem. 3.2.3/4] for the étale case.
We fix some notation for the remainder of the article. Consider the differential operator
![]() $\partial := \partial _{\mathrm {inv}}= \frac {1}{\log _{LT}'(Z)}\frac {d}{dZ}$
acting on
$\partial := \partial _{\mathrm {inv}}= \frac {1}{\log _{LT}'(Z)}\frac {d}{dZ}$
acting on
![]() $\mathcal {R}_K.$
(This differs from [Reference Colmez15] by a constant.) Let
$\mathcal {R}_K.$
(This differs from [Reference Colmez15] by a constant.) Let
![]() ${\nabla \in Lie(\Gamma _L)\cong L}$
be the element corresponding to
${\nabla \in Lie(\Gamma _L)\cong L}$
be the element corresponding to
![]() $1 \in L.$
$1 \in L.$
Remark 3.12. We obtain the following properties (cf. [Reference Colmez15, 1.2.4]):
-
(i)
 $\partial \circ \varphi = \pi _L \varphi \circ \partial .$
$\partial \circ \varphi = \pi _L \varphi \circ \partial .$
-
(ii)
 $\partial \circ \gamma = \chi _{LT}(\gamma ) \gamma \circ \partial .$
$\partial \circ \gamma = \chi _{LT}(\gamma ) \gamma \circ \partial .$
-
(iii)
 $\nabla f = t_{LT}\partial f$
for
$\nabla f = t_{LT}\partial f$
for
 $f\in \mathcal {R}_K.$
$f\in \mathcal {R}_K.$
-
(iv)
 $\nabla (f\mathbf {e}_\delta ) = (\nabla f+\omega _{\delta }f)\mathbf {e}_\delta $
for
$\nabla (f\mathbf {e}_\delta ) = (\nabla f+\omega _{\delta }f)\mathbf {e}_\delta $
for
 $\delta \in \Sigma _{an}.$
$\delta \in \Sigma _{an}.$
-
(v)
 $\partial \eta (x,T) = \Omega x \eta (x,T)$
$\partial \eta (x,T) = \Omega x \eta (x,T)$
3.5 The modules
 $\mathbf {D}_{\mathrm {dif}}^{(+)}(M)$
$\mathbf {D}_{\mathrm {dif}}^{(+)}(M)$
We set
![]() $t_{LT}=\log _{LT}(Z) \in L[[Z]]$
, so that
$t_{LT}=\log _{LT}(Z) \in L[[Z]]$
, so that
by (3). For
![]() $n\geq 1$
, we set
$n\geq 1$
, we set
Then
![]() $[\pi _L^n](u_n+_{LT}\exp _{LT}(\frac {t_{LT}}{\pi _L^n}))=Z,$
which is how Colmez justifies this notation in [Reference Colmez15, 1.4.2]. Note that the constant term of
$[\pi _L^n](u_n+_{LT}\exp _{LT}(\frac {t_{LT}}{\pi _L^n}))=Z,$
which is how Colmez justifies this notation in [Reference Colmez15, 1.4.2]. Note that the constant term of
![]() $[\pi _L^{-n}](Z)$
is equal to
$[\pi _L^{-n}](Z)$
is equal to
![]() $u_n$
and hence is non-zero, so
$u_n$
and hence is non-zero, so
![]() $[\pi _L^{-n}](Z)$
is a unit in
$[\pi _L^{-n}](Z)$
is a unit in
![]() $L_n[[Z]]$
.
$L_n[[Z]]$
.
Furthermore, let
![]() $\theta :K_n[[t_{LT}]]\to K_n$
denote the
$\theta :K_n[[t_{LT}]]\to K_n$
denote the
![]() $K_n$
-linear map sending
$K_n$
-linear map sending
![]() $t_{LT}$
to
$t_{LT}$
to
![]() $0,$
i.e., the reduction modulo
$0,$
i.e., the reduction modulo
![]() $t_{LT}.$
This is the completed base change to K of the restriction of
$t_{LT}.$
This is the completed base change to K of the restriction of
![]() $\theta :\mathbf {B}_{dR}^+\to \mathbb {C}_p$
to
$\theta :\mathbf {B}_{dR}^+\to \mathbb {C}_p$
to
![]() $L_n[[t_{LT}]]\to L_n.$
$L_n[[t_{LT}]]\to L_n.$
In the following, let F be a complete non-Archimedean field containing L.
Definition 3.13. The group
![]() $\Gamma _L$
acts diagonally on
$\Gamma _L$
acts diagonally on
(trivially on the right factor and naturally on the left), and we extend this to an action on
![]() $F_n[[Z]]$
via its usual action on Z.Footnote
4
Now define
$F_n[[Z]]$
via its usual action on Z.Footnote
4
Now define
 $$ \begin{align*} \iota_n=\iota_n^{(F)}:\mathcal{R}_F^{r_n} & \to F_n[[t_{LT}]]=F_n[[Z]], \\ \sum_{k\in\mathbb{Z}} a_kZ^k & \mapsto \sum_{k\in\mathbb{Z}} a_k([\pi_L^{-n}](Z))^k, \end{align*} $$
$$ \begin{align*} \iota_n=\iota_n^{(F)}:\mathcal{R}_F^{r_n} & \to F_n[[t_{LT}]]=F_n[[Z]], \\ \sum_{k\in\mathbb{Z}} a_kZ^k & \mapsto \sum_{k\in\mathbb{Z}} a_k([\pi_L^{-n}](Z))^k, \end{align*} $$
where on the right-hand side
![]() $a_k$
denotes (by abuse of notation) the image under the canonical embedding
$a_k$
denotes (by abuse of notation) the image under the canonical embedding ![]() and
and
![]() $[\pi _L^{-n}](Z)$
is viewed as a power series over
$[\pi _L^{-n}](Z)$
is viewed as a power series over
![]() $L_n\otimes _LF$
via the embedding
$L_n\otimes _LF$
via the embedding ![]() .
.
Remark 3.14.
-
(i) The map
 $\iota _n$
is well-defined.
$\iota _n$
is well-defined. -
(ii) For the power series
 $t_{LT}=\log _{LT}(Z )\in \mathcal {R}_F^+$
, we have
$t_{LT}=\log _{LT}(Z )\in \mathcal {R}_F^+$
, we have  $$ \begin{align*} \iota_n(t_{LT})=\frac{t_{LT}}{ \pi_L^n}. \end{align*} $$
$$ \begin{align*} \iota_n(t_{LT})=\frac{t_{LT}}{ \pi_L^n}. \end{align*} $$
-
(iii)
 $\iota _n$
is injective for every
$\iota _n$
is injective for every
 $n.$
Footnote
5
$n.$
Footnote
5
Proof. To see that
![]() $\iota _n$
is well-defined for
$\iota _n$
is well-defined for
![]() $F=L$
first recall that by [Reference Colmez14, Prop. 8.10], the ring
$F=L$
first recall that by [Reference Colmez14, Prop. 8.10], the ring
![]() $\mathbf {B}_{\mathrm {dR}}^+$
contains a period
$\mathbf {B}_{\mathrm {dR}}^+$
contains a period
![]() $t_L$
for the Lubin-Tate character, i.e. we have
$t_L$
for the Lubin-Tate character, i.e. we have
![]() $g(t_L)= \chi _{LT}(g)t_L$
for all
$g(t_L)= \chi _{LT}(g)t_L$
for all
![]() $g \in G_L$
and
$g \in G_L$
and
![]() $t_L$
differs from the usual t by a unit. Thus
$t_L$
differs from the usual t by a unit. Thus
![]() $L_n[[t_{LT}]]$
embeds into
$L_n[[t_{LT}]]$
embeds into
![]() $\mathbf {B}_{\mathrm {dR}}^+$
via
$\mathbf {B}_{\mathrm {dR}}^+$
via
![]() $t_{LT} \longmapsto t_L$
and we endow it with the subspace topology, making it a closed subspace of
$t_{LT} \longmapsto t_L$
and we endow it with the subspace topology, making it a closed subspace of
![]() $\mathbf {B}_{\mathrm {dR}}^+$
. It hence suffices to show that
$\mathbf {B}_{\mathrm {dR}}^+$
. It hence suffices to show that
![]() $\iota _n(f)$
converges in
$\iota _n(f)$
converges in
![]() $\mathbf {B}_{\mathrm {dR}}^+.$
A series of the form
$\mathbf {B}_{\mathrm {dR}}^+.$
A series of the form
![]() $x=\sum _{k \gg -\infty } p^k [x_k] \in W(o_{\mathbb {C}_p^\flat })[1/p]$
converges in
$x=\sum _{k \gg -\infty } p^k [x_k] \in W(o_{\mathbb {C}_p^\flat })[1/p]$
converges in
![]() $\mathbf {B}_{\mathrm {dR}}^+$
if and only if
$\mathbf {B}_{\mathrm {dR}}^+$
if and only if
![]() $\theta (x)$
converges in
$\theta (x)$
converges in
![]() $\mathbb {C}_p$
(which is the case precisely when
$\mathbb {C}_p$
(which is the case precisely when
![]() $k+v(x_k) \to \infty $
for
$k+v(x_k) \to \infty $
for
![]() $k \to \infty $
). As in [Reference Cherbonnier and Colmez12, Prop. III.2.1 (i)], the condition
$k \to \infty $
). As in [Reference Cherbonnier and Colmez12, Prop. III.2.1 (i)], the condition
![]() $x=\sum _{k \in \mathbb {Z}}a_k Z_u^k$
with
$x=\sum _{k \in \mathbb {Z}}a_k Z_u^k$
with
![]() $a_k \in o_L$
and
$a_k \in o_L$
and
![]() $v_p(a_k) + k \cdot r_n \to \infty $
for
$v_p(a_k) + k \cdot r_n \to \infty $
for
![]() $k \to -\infty $
implies that
$k \to -\infty $
implies that
![]() $\iota _n(x)$
converges in
$\iota _n(x)$
converges in
![]() $\mathbf {B}_{\mathrm {dR}}^+$
. Even though the coefficients of an element
$\mathbf {B}_{\mathrm {dR}}^+$
. Even though the coefficients of an element
![]() $x \in \mathcal {R}_L^{r_n} $
are not bounded, they do satisfy the same growth condition, which ensures the convergence of
$x \in \mathcal {R}_L^{r_n} $
are not bounded, they do satisfy the same growth condition, which ensures the convergence of
![]() $\iota _n(x).$
The case of general F is obtained via completed base change
$\iota _n(x).$
The case of general F is obtained via completed base change
![]() $\mathcal {R}_F^{r_n} = F \hat {\otimes }_{L,\pi }\mathcal {R}_L^{r_n} \to F_n[[t_{LT}]] = F \hat {\otimes }_{L,\pi }L_n[[t_{LT}]].$
$\mathcal {R}_F^{r_n} = F \hat {\otimes }_{L,\pi }\mathcal {R}_L^{r_n} \to F_n[[t_{LT}]] = F \hat {\otimes }_{L,\pi }L_n[[t_{LT}]].$
For the second point we compute
 $$ \begin{align*} \iota_n(t_{LT})=\log_{LT}([\pi_L^{-n}](Z)) =\underbrace{\log_{LT}(u_n)}_{=0}+\log_{LT}\exp_{LT}\left( \frac{t_{LT}}{\pi_L^n}\right)=\frac{t_{LT}}{ \pi_L^n}. \end{align*} $$
$$ \begin{align*} \iota_n(t_{LT})=\log_{LT}([\pi_L^{-n}](Z)) =\underbrace{\log_{LT}(u_n)}_{=0}+\log_{LT}\exp_{LT}\left( \frac{t_{LT}}{\pi_L^n}\right)=\frac{t_{LT}}{ \pi_L^n}. \end{align*} $$
For the injectivity of
![]() $\iota _n$
we can assume
$\iota _n$
we can assume
![]() $F=L$
because completed base change
$F=L$
because completed base change
![]() $F \hat {\otimes }_{L,\pi }-$
preserves injectivity by [Reference Emerton19, 1.1.26]. Consider
$F \hat {\otimes }_{L,\pi }-$
preserves injectivity by [Reference Emerton19, 1.1.26]. Consider ![]() the reduction modulo
the reduction modulo
![]() $t_{LT}$
such that
$t_{LT}$
such that
![]() $\theta \circ \iota _n(f)=f(u_n).$
If
$\theta \circ \iota _n(f)=f(u_n).$
If
![]() $\iota _n(f)=0$
then
$\iota _n(f)=0$
then
![]() $f(u_n)=0$
and hence f is divisible by
$f(u_n)=0$
and hence f is divisible by
![]() $Q_n(Z):=\frac {[\pi _L^n](Z)}{[\pi _L^{n-1}](Z)}.$
Because
$Q_n(Z):=\frac {[\pi _L^n](Z)}{[\pi _L^{n-1}](Z)}.$
Because
![]() $\iota _n(t_{LT})\neq 0$
and
$\iota _n(t_{LT})\neq 0$
and
![]() $Q_n \mid t_{LT} = Z\prod _{\mu \geq 1}\frac {Q_\mu } {\pi _L}$
we conclude
$Q_n \mid t_{LT} = Z\prod _{\mu \geq 1}\frac {Q_\mu } {\pi _L}$
we conclude
![]() $\iota _n(Q_n)\neq 0$
and hence
$\iota _n(Q_n)\neq 0$
and hence
![]() $\iota _n(f/Q_n)=0.$
Inductively
$\iota _n(f/Q_n)=0.$
Inductively
![]() $Q_n^k \mid f$
for every
$Q_n^k \mid f$
for every
![]() $k\geq 0.$
The choice of n ensures that
$k\geq 0.$
The choice of n ensures that
![]() $Q_n \in \mathcal {R}_L^{r_n}$
is a non-unit. By considering the image of f in the noetherian domain
$Q_n \in \mathcal {R}_L^{r_n}$
is a non-unit. By considering the image of f in the noetherian domain
![]() $\mathcal {R}_L^{[r_n,r_n]}$
under the inclusion
$\mathcal {R}_L^{[r_n,r_n]}$
under the inclusion
![]() $\mathcal {R}_L^{r_n}\subset \mathcal {R}_L^{[r_n,r_n]}$
we conclude
$\mathcal {R}_L^{r_n}\subset \mathcal {R}_L^{[r_n,r_n]}$
we conclude
![]() $f=0$
by Krull’s Intersection Theorem.
$f=0$
by Krull’s Intersection Theorem.
The map
![]() $\iota _n$
commutes with the action of
$\iota _n$
commutes with the action of
![]() $\Gamma _L$
. Writing
$\Gamma _L$
. Writing
![]() $\mathrm {Tr}=\operatorname {id}_F\otimes \frac {1}{q}\mathrm {Tr}_{L_{n+1}/L_n}$
we obtain the commutative diagrams
$\mathrm {Tr}=\operatorname {id}_F\otimes \frac {1}{q}\mathrm {Tr}_{L_{n+1}/L_n}$
we obtain the commutative diagrams

and

Definition 3.15. Let M be a
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_F$
. Viewing
$\mathcal {R}_F$
. Viewing
![]() $F_{n}[[t_{LT}]]$
as an
$F_{n}[[t_{LT}]]$
as an
![]() $\mathcal {R}_F^{r_n}$
-module via
$\mathcal {R}_F^{r_n}$
-module via
![]() $\iota _n$
, we define the
$\iota _n$
, we define the
![]() $F_{n}[[t_{LT}]]$
- and
$F_{n}[[t_{LT}]]$
- and
![]() $F_{n}((t_{LT}))$
-modules
$F_{n}((t_{LT}))$
-modules
respectively, where
![]() $(-)_{t_{LT}}$
means localising an
$(-)_{t_{LT}}$
means localising an
![]() $F_n[[t_{LT}]]$
-module at the multiplicative subset generated by
$F_n[[t_{LT}]]$
-module at the multiplicative subset generated by
![]() $t_{LT}$
. Furthermore,
$t_{LT}$
. Furthermore,
![]() $\mathbf {D}_{\text {dif},n}^+(M)$
carries the diagonal action of
$\mathbf {D}_{\text {dif},n}^+(M)$
carries the diagonal action of
![]() $\Gamma _L$
, which also extends to
$\Gamma _L$
, which also extends to
![]() $\mathbf {D}_{\text {dif},n}(M)$
. Under the isomorphism
$\mathbf {D}_{\text {dif},n}(M)$
. Under the isomorphism
![]() $\varphi ^{*}(M^{(n)}) = \mathcal {R}_F^{r_{n+1}} \otimes _{\varphi ,\mathcal {R}^{r_n}_F} M^{(n)} \cong M^{(n+1)}$
, the map
$\varphi ^{*}(M^{(n)}) = \mathcal {R}_F^{r_{n+1}} \otimes _{\varphi ,\mathcal {R}^{r_n}_F} M^{(n)} \cong M^{(n+1)}$
, the map
![]() $\varphi \colon M^{(n)} \to M^{(n+1)}$
corresponds to the canonical map
$\varphi \colon M^{(n)} \to M^{(n+1)}$
corresponds to the canonical map
![]() $\operatorname {can_{n,n+1}}\colon M^{(n)}\to \varphi ^{*}(M^{(n)}); x\mapsto 1 \otimes x.$
The above diagrams then induce the diagrams (see [Reference Nakamura36, §2.B] for details)
$\operatorname {can_{n,n+1}}\colon M^{(n)}\to \varphi ^{*}(M^{(n)}); x\mapsto 1 \otimes x.$
The above diagrams then induce the diagrams (see [Reference Nakamura36, §2.B] for details)

where the map
![]() $\mathrm {can}_{n,n+1}$
is given by
$\mathrm {can}_{n,n+1}$
is given by ![]() , and
, and
![]() $\iota _n$
by
$\iota _n$
by
![]() $m\mapsto 1\otimes m$
, as well as, for
$m\mapsto 1\otimes m$
, as well as, for
![]() $n\geq 1,$
$n\geq 1,$

with transitions maps
![]() $f(t)\otimes x\mapsto \mathrm {Tr}(f(t))\otimes \psi (x)$
on the right hand side. Finally, we define
$f(t)\otimes x\mapsto \mathrm {Tr}(f(t))\otimes \psi (x)$
on the right hand side. Finally, we define
with
![]() $\mathrm {can}_{n,n+1}$
as transition maps.
$\mathrm {can}_{n,n+1}$
as transition maps.
As in [Reference Nakamura36], we have
![]() $\mathbf {D}_{\text {dif},n}^{+}(M) \otimes _{F_n[[t_{LT}]]} F_{n+1}[[t_{LT}]] \overset {\sim }{\longrightarrow } \mathbf {D}_{\text {dif},n+1}^{+}(M)$
and hence
$\mathbf {D}_{\text {dif},n}^{+}(M) \otimes _{F_n[[t_{LT}]]} F_{n+1}[[t_{LT}]] \overset {\sim }{\longrightarrow } \mathbf {D}_{\text {dif},n+1}^{+}(M)$
and hence
for
![]() $n \gg 0$
.
$n \gg 0$
.
Remark 3.16. Since
![]() $M^{(n)}$
is a free module over
$M^{(n)}$
is a free module over
![]() $\mathcal {R}_F^{(n)}$
, say of rank d, we have
$\mathcal {R}_F^{(n)}$
, say of rank d, we have
![]() $\mathbf {D}_{\mathrm {dif},n}^+(M)\cong F_n[[t_{LT}]]^d$
. The Fréchet-space-structure on
$\mathbf {D}_{\mathrm {dif},n}^+(M)\cong F_n[[t_{LT}]]^d$
. The Fréchet-space-structure on
![]() $F_n[[t_{LT}]]=\varprojlim F_n[[t_{LT}]]/(t_{LT}^k)$
(with base field
$F_n[[t_{LT}]]=\varprojlim F_n[[t_{LT}]]/(t_{LT}^k)$
(with base field
![]() $F,$
where each factor is a finite-dimensional F-vector space endowed with it’s canonical topology) thus induces one on
$F,$
where each factor is a finite-dimensional F-vector space endowed with it’s canonical topology) thus induces one on
![]() $\mathbf {D}_{\mathrm {dif},n}^+(M)$
, which is of course independent of the choice of the isomorphism above. Furthermore,
$\mathbf {D}_{\mathrm {dif},n}^+(M)$
, which is of course independent of the choice of the isomorphism above. Furthermore,
![]() $\mathbf {D}_{\mathrm {dif},n}(M)=\varinjlim _{k}\mathbf {D}_{\mathrm {dif},n}^+(M)\cdot t_{LT}^{-k}$
becomes an LF-space over F in this way. Finally, the modules
$\mathbf {D}_{\mathrm {dif},n}(M)=\varinjlim _{k}\mathbf {D}_{\mathrm {dif},n}^+(M)\cdot t_{LT}^{-k}$
becomes an LF-space over F in this way. Finally, the modules
![]() $\mathbf {D}_{\mathrm {dif}}^+(M)$
and
$\mathbf {D}_{\mathrm {dif}}^+(M)$
and
![]() $\mathbf {D}_{\mathrm {dif}}(M)$
are also LF-spacesFootnote
6
over F.
$\mathbf {D}_{\mathrm {dif}}(M)$
are also LF-spacesFootnote
6
over F.
Later on it will be crucial to form the cohomology groups
![]() $H^i_{\varphi , \mathfrak {Z}}(\mathbf {D}_{\mathrm {dif}}^+(M))$
from Section 4. For this we need a
$H^i_{\varphi , \mathfrak {Z}}(\mathbf {D}_{\mathrm {dif}}^+(M))$
from Section 4. For this we need a
![]() $D(\Gamma _L,F)$
-module-structure on
$D(\Gamma _L,F)$
-module-structure on
![]() $\mathbf {D}_{\mathrm {dif}}^{(+)}(M)$
, which we get from Proposition 3.18 below after showing that the action is pro-L-analytic. Let us first recall this notion.
$\mathbf {D}_{\mathrm {dif}}^{(+)}(M)$
, which we get from Proposition 3.18 below after showing that the action is pro-L-analytic. Let us first recall this notion.
Definition 3.17. Let G be an L-analytic group (the main example to have in mind is
![]() $G=\Gamma _L$
).
$G=\Gamma _L$
).
-
(a) Let V be a Banach space over F equipped with a continuous linear G-action. We say that a vector
 $v\in V$
is locally L
-analytic if there exists an open subgroup
$v\in V$
is locally L
-analytic if there exists an open subgroup
 $\Gamma _n\subseteq G$
together with a chart
$\Gamma _n\subseteq G$
together with a chart
 $\ell \colon \Gamma _n\overset \sim \to \pi _L^n o_L$
(for some
$\ell \colon \Gamma _n\overset \sim \to \pi _L^n o_L$
(for some
 $n\geq 0$
) such that the orbit map of v restricted to
$n\geq 0$
) such that the orbit map of v restricted to
 $\Gamma _n$
is given by a power series
$\Gamma _n$
is given by a power series  $$ \begin{align*} \gamma(v)=\sum_{k\geq 0}\ell(\gamma)^k v_k \end{align*} $$
$$ \begin{align*} \gamma(v)=\sum_{k\geq 0}\ell(\gamma)^k v_k \end{align*} $$
where
 $v_k\in V$
is a sequence of vectors satisfying
$v_k\in V$
is a sequence of vectors satisfying
 $\pi _L^{nk}v_k\to 0$
for
$\pi _L^{nk}v_k\to 0$
for
 $k\to \infty $
. We say that the action of G is locally L
-analytic if all
$k\to \infty $
. We say that the action of G is locally L
-analytic if all
 $v\in V$
are locally L-analytic.
$v\in V$
are locally L-analytic. -
(b) Let
 $W=\varinjlim _m W_m$
be an LF-space over F, with Fréchet spaces
$W=\varinjlim _m W_m$
be an LF-space over F, with Fréchet spaces
 $W_m=\varprojlim _n W_{m,n}$
and Banach spaces
$W_m=\varprojlim _n W_{m,n}$
and Banach spaces
 $W_{m,n}$
, such that G acts linearly and continuously on W. We say that a vector
$W_{m,n}$
, such that G acts linearly and continuously on W. We say that a vector
 $w\in W$
is pro- L
-analytic if its orbit map
$w\in W$
is pro- L
-analytic if its orbit map
 $G\to W$
factors over some
$G\to W$
factors over some
 $W_m$
and the induced maps
$W_m$
and the induced maps
 $G\to W_{m,n}$
are locally L-analytic for all n. We denote by
$G\to W_{m,n}$
are locally L-analytic for all n. We denote by
 $W^{L-pa}$
the subset of pro-L-analytic vectors of
$W^{L-pa}$
the subset of pro-L-analytic vectors of
 $W.$
We say the action is pro-
L
-analytic if
$W.$
We say the action is pro-
L
-analytic if
 $W^{L-pa}=W.$
$W^{L-pa}=W.$
Proposition 3.18. Let W be an LF-space over F carrying a pro-L-analytic action of
![]() $\Gamma _L$
. Then this action extends uniquely to a separately continuous action of
$\Gamma _L$
. Then this action extends uniquely to a separately continuous action of
![]() $D(\Gamma _L,F)$
on W.
$D(\Gamma _L,F)$
on W.
Proof. This follows from the proof of [Reference Schneider and Venjakob46, Proposition 4.3.10].
Lemma 3.19. Let B be a Fréchet
![]() $\Gamma _L$
-ring over F and W a finitely generated free B-module with a compatible
$\Gamma _L$
-ring over F and W a finitely generated free B-module with a compatible
![]() $\Gamma _L$
-action. Assume there is a basis
$\Gamma _L$
-action. Assume there is a basis
![]() ${\mathfrak {A}}:=(e_1,\ldots ,e_d)$
for W such that the map
${\mathfrak {A}}:=(e_1,\ldots ,e_d)$
for W such that the map
is pro-L-analytic.
![]() $W^{L-\mathrm {pa}}=\bigoplus _{j=1}^dB^{L-\mathrm {pa}}\cdot e_j$
.
$W^{L-\mathrm {pa}}=\bigoplus _{j=1}^dB^{L-\mathrm {pa}}\cdot e_j$
.
Proof. This is proven for
![]() $F=L=\mathbb {Q}_p$
in [Reference Berger5, Prop. 2.4] and the identical proof applies for general F and L.
$F=L=\mathbb {Q}_p$
in [Reference Berger5, Prop. 2.4] and the identical proof applies for general F and L.
Proposition 3.20. For an L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_F$
, the
$\mathcal {R}_F$
, the
![]() $\Gamma _L$
-action on the LF-spaces
$\Gamma _L$
-action on the LF-spaces
![]() $\operatorname {{{\mathbf {D}}_{\mathrm {dif}}^+}}(M)$
and
$\operatorname {{{\mathbf {D}}_{\mathrm {dif}}^+}}(M)$
and
![]() $\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(M)$
is pro-L-analytic.
$\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(M)$
is pro-L-analytic.
Proof. We start with
![]() $\operatorname {{{\mathbf {D}}_{\mathrm {dif}}^+}}(M)=\varinjlim _{n\gg 0}\mathbf {D}_{\mathrm {dif},n}^+(M)$
. By definition, it suffices to check that the
$\operatorname {{{\mathbf {D}}_{\mathrm {dif}}^+}}(M)=\varinjlim _{n\gg 0}\mathbf {D}_{\mathrm {dif},n}^+(M)$
. By definition, it suffices to check that the
![]() $\Gamma _L$
-action on the Fréchet space
$\Gamma _L$
-action on the Fréchet space
![]() $\mathbf {D}_{\mathrm {dif},n}^+(M)$
is pro-L-analytic for
$\mathbf {D}_{\mathrm {dif},n}^+(M)$
is pro-L-analytic for
![]() $n\gg 0$
.
$n\gg 0$
.
We wish to apply Lemma 3.19 with
![]() $B:=F_n[[t_{LT}]]$
and
$B:=F_n[[t_{LT}]]$
and
![]() $W:=\mathbf {D}_{\mathrm {dif},n}^+(M)=B\otimes _{\mathcal {R}_F^{(n)}}M^{(n)}$
: Choose any
$W:=\mathbf {D}_{\mathrm {dif},n}^+(M)=B\otimes _{\mathcal {R}_F^{(n)}}M^{(n)}$
: Choose any
![]() $\mathcal {R}_F^{(n)}$
-module basis
$\mathcal {R}_F^{(n)}$
-module basis
![]() $x_1,\dots ,x_d$
of
$x_1,\dots ,x_d$
of
![]() $M^{(n)}$
. Then
$M^{(n)}$
. Then
![]() ${\mathfrak {A}}:=(1\otimes x_1,\ldots ,1\otimes x_d)$
is a basis of the free B-module W, and the map
${\mathfrak {A}}:=(1\otimes x_1,\ldots ,1\otimes x_d)$
is a basis of the free B-module W, and the map
![]() $\gamma \longmapsto \mathrm {Mat}_{{\mathfrak {A}}}(\gamma )$
is given by the composite
$\gamma \longmapsto \mathrm {Mat}_{{\mathfrak {A}}}(\gamma )$
is given by the composite
where the first map is pro-L-analytic because
![]() $M^{(n)}$
is pro-L-analytic by assumption. Moreover, since
$M^{(n)}$
is pro-L-analytic by assumption. Moreover, since
![]() $\iota _n$
is a continuous homomorphism of F-algebras, we conclude that 3.19 is applicable. Thus we obtain
$\iota _n$
is a continuous homomorphism of F-algebras, we conclude that 3.19 is applicable. Thus we obtain
 $$ \begin{align*} W^{L-\mathrm{pa}}=\bigoplus_{j=1}^d B^{L-\mathrm{pa}}\cdot (1\otimes x_j)= F_n[[t_{LT}]]^{L-\mathrm{pa}}\otimes_{\mathcal{R}_F^{(n)}}M^{(n)}. \end{align*} $$
$$ \begin{align*} W^{L-\mathrm{pa}}=\bigoplus_{j=1}^d B^{L-\mathrm{pa}}\cdot (1\otimes x_j)= F_n[[t_{LT}]]^{L-\mathrm{pa}}\otimes_{\mathcal{R}_F^{(n)}}M^{(n)}. \end{align*} $$
Finally, from [Reference Porat38, Prop. 2.6 2.] it follows that
![]() $F_n[[t_{LT}]]^{L-\mathrm {pa}}=F_n[[t_{LT}]]$
, which completes the proof for
$F_n[[t_{LT}]]^{L-\mathrm {pa}}=F_n[[t_{LT}]]$
, which completes the proof for
![]() $\operatorname {{{\mathbf {D}}_{\mathrm {dif}}^+}}(M)$
.
$\operatorname {{{\mathbf {D}}_{\mathrm {dif}}^+}}(M)$
.
Moving on to
![]() $\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(M)$
, we write
$\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(M)$
, we write
![]() $\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(M)=\varinjlim _{n,k}\mathbf {D}_{\mathrm {dif},n}^+(M)\cdot t_{LT}^{-k}$
as a direct limit of Fréchet spaces. By what we have just shown, one can express
$\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(M)=\varinjlim _{n,k}\mathbf {D}_{\mathrm {dif},n}^+(M)\cdot t_{LT}^{-k}$
as a direct limit of Fréchet spaces. By what we have just shown, one can express
![]() $\mathbf {D}_{\mathrm {dif},n}^+(M)$
for
$\mathbf {D}_{\mathrm {dif},n}^+(M)$
for
![]() $n\gg 0$
as inverse limit
$n\gg 0$
as inverse limit
![]() $\mathbf {D}_{\mathrm {dif},n}^+(M)=\varprojlim _r B_{n,r}$
for certain F-Banach spaces
$\mathbf {D}_{\mathrm {dif},n}^+(M)=\varprojlim _r B_{n,r}$
for certain F-Banach spaces
![]() $B_{n,r}$
on which
$B_{n,r}$
on which
![]() $\Gamma _L$
acts L-analytically. So for any k one has
$\Gamma _L$
acts L-analytically. So for any k one has
where by
![]() $B_{n,r}\cdot t_{LT}^{-k}$
we denote the
$B_{n,r}\cdot t_{LT}^{-k}$
we denote the
![]() $\Gamma _L $
-module
$\Gamma _L $
-module
![]() $B_{n,r}$
whose
$B_{n,r}$
whose
![]() $\Gamma _L$
-action is twisted by
$\Gamma _L$
-action is twisted by
![]() $\chi _{LT}^{-k}$
. Since the inversion in
$\chi _{LT}^{-k}$
. Since the inversion in
![]() $\Gamma _L$
is an L-analytic map, we see that the twisted action
$\Gamma _L$
is an L-analytic map, we see that the twisted action
![]() $b\longmapsto \chi _{LT}(\gamma ^{-k})\cdot \gamma (b)$
on
$b\longmapsto \chi _{LT}(\gamma ^{-k})\cdot \gamma (b)$
on
![]() $B_{n,r}$
is again L-analytic. Thus
$B_{n,r}$
is again L-analytic. Thus
![]() $\Gamma _L $
acts pro-L-analytically on
$\Gamma _L $
acts pro-L-analytically on
![]() $\mathbf {D}_{\mathrm {dif},n}^+(M)\cdot t_{LT}^{-k}$
for
$\mathbf {D}_{\mathrm {dif},n}^+(M)\cdot t_{LT}^{-k}$
for
![]() $n\gg 0$
and
$n\gg 0$
and
![]() $k\geq 1$
, so the claim follows.
$k\geq 1$
, so the claim follows.
Note that
![]() $\mathbf {D}_{\mathrm {dif}}(M)$
depends on the coefficient field of
$\mathbf {D}_{\mathrm {dif}}(M)$
depends on the coefficient field of
![]() $\mathcal {R}_F.$
For a complete field extension
$\mathcal {R}_F.$
For a complete field extension
![]() $F'/F$
and an L-analytic
$F'/F$
and an L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_F$
one checks that
$\mathcal {R}_F$
one checks that
![]() $F' \hat {\otimes }_{F,i}M$
is an L-analytic
$F' \hat {\otimes }_{F,i}M$
is an L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_{F'}.$
Here
$\mathcal {R}_{F'}.$
Here
![]() $\hat {\otimes }_{F,i}$
denotes the inductive tensor product topology.
$\hat {\otimes }_{F,i}$
denotes the inductive tensor product topology.
Remark 3.21. Let
![]() $F'/F$
be a complete field extension and let M be an L-analytic
$F'/F$
be a complete field extension and let M be an L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_F.$
The natural maps
$\mathcal {R}_F.$
The natural maps
and
are
![]() $\Gamma _L$
-equivariant isomorphisms.
$\Gamma _L$
-equivariant isomorphisms.
Proof. The completed inductive tensor product commutes with strict locally convex inductive limits by [Reference Emerton19, Theorem 1.1.30] together with the argument in the proof of [Reference Berger, Schneider and Xie7, 2.1.7(i)]. Hence the first statement follows from the second. For Fréchet spaces inductive and projective tensor products agree and commute with projective limits (of Hausdorff spaces) with dense transition maps (cf. [Reference Berger, Schneider and Xie7, 2.1.4] and [Reference Schneider40, 17.6]). This allows us to first reduce to the corresponding statement for
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}},n}^+(M)t_{LT}^{-k_0}$
since
$\mathbf {D}_{\operatorname {\mathrm {dif}},n}^+(M)t_{LT}^{-k_0}$
since
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}},n}(M) = \varinjlim _k \mathbf {D}_{\operatorname {\mathrm {dif}},n}^+(M)t_{LT}^{-k}$
and by 3.16 we have
$\mathbf {D}_{\operatorname {\mathrm {dif}},n}(M) = \varinjlim _k \mathbf {D}_{\operatorname {\mathrm {dif}},n}^+(M)t_{LT}^{-k}$
and by 3.16 we have
![]() $\mathbf {D}^+_{\mathrm {dif},n}(M) \cong \varprojlim _k \mathbf {D}^+_{\mathrm {dif},n}(M)/(t_{LT}^k)$
, hence we even have surjective transition maps which allow us to reduce to the corresponding statement for
$\mathbf {D}^+_{\mathrm {dif},n}(M) \cong \varprojlim _k \mathbf {D}^+_{\mathrm {dif},n}(M)/(t_{LT}^k)$
, hence we even have surjective transition maps which allow us to reduce to the corresponding statement for
![]() $\mathbf {D}^+_{\mathrm {dif},n}(M)/(t_{LT}^k)$
(assuming for simplicity
$\mathbf {D}^+_{\mathrm {dif},n}(M)/(t_{LT}^k)$
(assuming for simplicity
![]() $k_0=0$
, the general case being treated analogously). Since each
$k_0=0$
, the general case being treated analogously). Since each
![]() $\mathbf {D}^+_{\mathrm {dif},n}(M)/(t_{LT}^k)$
is finite dimensional over F, we may omit the completion and see that
$\mathbf {D}^+_{\mathrm {dif},n}(M)/(t_{LT}^k)$
is finite dimensional over F, we may omit the completion and see that
is an isomorphism of finite dimensional
![]() $F'$
-vector spaces, which follows from the fact that any basis of
$F'$
-vector spaces, which follows from the fact that any basis of
![]() $M^{(n)}$
gives rise on the one hand to a
$M^{(n)}$
gives rise on the one hand to a
![]() $F_n[[t_{LT}]]$
basis of
$F_n[[t_{LT}]]$
basis of
![]() $\mathbf {D}^+_{\mathrm {dif},n}(M)$
and on the other hand to a basis of
$\mathbf {D}^+_{\mathrm {dif},n}(M)$
and on the other hand to a basis of
![]() $F'\hat {\otimes }M^{(n)}$
and thus to a
$F'\hat {\otimes }M^{(n)}$
and thus to a
![]() $F^{\prime }_n[[t_{LT}]]$
basis of
$F^{\prime }_n[[t_{LT}]]$
basis of
![]() $\mathbf {D}^+_{\mathrm {dif},n}(F'\hat {\otimes }M).$
Note that
$\mathbf {D}^+_{\mathrm {dif},n}(F'\hat {\otimes }M).$
Note that
![]() $F_n[[t_{LT}]]/(t_{LT})^k \otimes _F F' \cong F^{\prime }_n[[t_{LT}]]/(t_{LT})^k$
by a dimension argument.
$F_n[[t_{LT}]]/(t_{LT})^k \otimes _F F' \cong F^{\prime }_n[[t_{LT}]]/(t_{LT})^k$
by a dimension argument.
Lemma 3.22. Let V be a F-Banach space and let G be a group acting on V via continuous F-linear maps. Let W be an F-Banach space of countable type endowed with the trivial G-action. Then
Proof. Assume without loss of generality, that W is infinite dimensional (the finite dimensional case being simpler). By [Reference Perez-Garcia and Schikhof37, Corollary 2.3.9] W is isomorphic to
![]() $c_0(F),$
the space of zero sequences in F indexed by
$c_0(F),$
the space of zero sequences in F indexed by
![]() $\mathbb {N}$
. We obtain a G-equivariant isomorphism
$\mathbb {N}$
. We obtain a G-equivariant isomorphism
![]() $V \hat {\otimes }W \cong c_0(V)$
by first identifying
$V \hat {\otimes }W \cong c_0(V)$
by first identifying
![]() $c_0(F)$
(resp. (
$c_0(F)$
(resp. (
![]() $c_0(V)$
)) with the completion of
$c_0(V)$
)) with the completion of
![]() $\bigoplus _{n \in \mathbb {N}}F$
(resp.
$\bigoplus _{n \in \mathbb {N}}F$
(resp.
![]() $\bigoplus _{n \in \mathbb {N}}V$
) and using the G-equivariant isomorphism
$\bigoplus _{n \in \mathbb {N}}V$
) and using the G-equivariant isomorphism
![]() $(\bigoplus _{n \in \mathbb {N}} F)\otimes _F V \cong \bigoplus _{n \in \mathbb {N}} V$
and passing to completions. Note that
$(\bigoplus _{n \in \mathbb {N}} F)\otimes _F V \cong \bigoplus _{n \in \mathbb {N}} V$
and passing to completions. Note that
![]() $g \in G$
acts via continuous automorphisms with respect to the product topology and hence extends to an automorphism of the completions with g acting on a sequence
$g \in G$
acts via continuous automorphisms with respect to the product topology and hence extends to an automorphism of the completions with g acting on a sequence
![]() $(v_1,v_2,\dots )$
via
$(v_1,v_2,\dots )$
via
![]() $g(v_1,v_2,\dots )= (gv_1,gv_2,\dots ).$
It is clear that any such sequence is G-invariant if and only if each component is G-invariant.
$g(v_1,v_2,\dots )= (gv_1,gv_2,\dots ).$
It is clear that any such sequence is G-invariant if and only if each component is G-invariant.
Corollary 3.23. Let
![]() $F'/F$
be a complete field extension contained in
$F'/F$
be a complete field extension contained in
![]() $\mathbb {C}_p$
and let M be an L-analytic
$\mathbb {C}_p$
and let M be an L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_F.$
We have
$\mathcal {R}_F.$
We have
Proof. Like in the proof of 3.21 we reduce to the corresponding statement for the Banach spaces
![]() $\mathbf {D}_{\mathrm {dif},n}(M)^+t_{LT}^{-k_0}/\mathbf {D}_{\mathrm {dif},n}(M)^+t_{LT}^{k-k_0}$
. The field
$\mathbf {D}_{\mathrm {dif},n}(M)^+t_{LT}^{-k_0}/\mathbf {D}_{\mathrm {dif},n}(M)^+t_{LT}^{k-k_0}$
. The field
![]() $F'$
is of countable type over F since
$F'$
is of countable type over F since
![]() $F'\cap \overline {\mathbb {Q}_p}$
is dense in
$F'\cap \overline {\mathbb {Q}_p}$
is dense in
![]() $F'$
by [Reference Iovita and Zaharescu26, Theorem 1] (and of at most countable dimension over
$F'$
by [Reference Iovita and Zaharescu26, Theorem 1] (and of at most countable dimension over
![]() $\mathbb {Q}_p$
) and hence also
$\mathbb {Q}_p$
) and hence also
![]() $F(F'\cap \overline {\mathbb {Q}_p})$
is a dense F-subspace of at most countable F-dimension. Because the action on
$F(F'\cap \overline {\mathbb {Q}_p})$
is a dense F-subspace of at most countable F-dimension. Because the action on
![]() $F'$
is trivial, we can deduce the result from 3.22.
$F'$
is trivial, we can deduce the result from 3.22.
4 (Analytic) Cohomology groups
For the moment let F be any field extension of L and G be any L-analytic group (of dimension one); we shall reserve the letter U for a (sub)group isomorphic to
![]() $o_L$
. If K is big enough such that
$o_L$
. If K is big enough such that
![]() $D(U):=D(U,K)\cong \mathcal {R}_K^+=: \mathcal {R}^+$
then we denote by
$D(U):=D(U,K)\cong \mathcal {R}_K^+=: \mathcal {R}^+$
then we denote by
![]() ${\mathfrak {Z}}\in D(U)$
the element corresponding to the variable
${\mathfrak {Z}}\in D(U)$
the element corresponding to the variable
![]() $Z\in \mathcal {R}^+$
. Let V be any (abstract)
$Z\in \mathcal {R}^+$
. Let V be any (abstract)
![]() $D(G,F)$
-module. We define cohomology groups
$D(G,F)$
-module. We define cohomology groups
![]() $H^\bullet _{\clubsuit ,\spadesuit }(V)$
for
$H^\bullet _{\clubsuit ,\spadesuit }(V)$
for
![]() $\clubsuit \in \{\varphi ,\psi \}$
and
$\clubsuit \in \{\varphi ,\psi \}$
and
![]() $\spadesuit \in \{D(G,F),{\mathfrak {Z}}, Lie(G),\nabla \}$
as follows: By
$\spadesuit \in \{D(G,F),{\mathfrak {Z}}, Lie(G),\nabla \}$
as follows: By
![]() $\mathrm {RHom}_{D(G)}(F,V)$
we denote any (bounded) complex of F-vector spaces whose cohomology gives
$\mathrm {RHom}_{D(G)}(F,V)$
we denote any (bounded) complex of F-vector spaces whose cohomology gives
![]() $\mathrm {Ext}_{D(G)}^\bullet (F,V)$
(extensions as abstract
$\mathrm {Ext}_{D(G)}^\bullet (F,V)$
(extensions as abstract
![]() $D(G)$
-modules). Let f be any endomorphism of V which commutes with the
$D(G)$
-modules). Let f be any endomorphism of V which commutes with the
![]() $D(G)$
-action inducing an operator on
$D(G)$
-action inducing an operator on
![]() $\mathrm {RHom}_{D(G)}(F,V)$
and we denote by
$\mathrm {RHom}_{D(G)}(F,V)$
and we denote by
the induced mapping fibre. For
![]() $U\cong o_L$
and K being big enough
$U\cong o_L$
and K being big enough
is a projective resolution of the trivial representation K and we can choose
![]() $V\xrightarrow {{\mathfrak {Z}}}V$
(functorially) for
$V\xrightarrow {{\mathfrak {Z}}}V$
(functorially) for
![]() $\mathrm {RHom}_{D(U)}(K,V)$
. In this context we shall also use the notation
$\mathrm {RHom}_{D(U)}(K,V)$
. In this context we shall also use the notation
![]() $K_{f,{\mathfrak {Z}}}(V)$
for
$K_{f,{\mathfrak {Z}}}(V)$
for
![]() $K_{f,D(U)}(V).$
Note that
$K_{f,D(U)}(V).$
Note that
as
![]() $ \mathrm {RHom}_{D(G)}(K,V)\cong V\otimes ^{\mathbb {L}}_{D(G)}K[-1] .$
Analogous isomorphisms exist for
$ \mathrm {RHom}_{D(G)}(K,V)\cong V\otimes ^{\mathbb {L}}_{D(G)}K[-1] .$
Analogous isomorphisms exist for
![]() $K_{f,D(G)}(V)$
for any G of dimension one, since in our context taking
$K_{f,D(G)}(V)$
for any G of dimension one, since in our context taking
![]() $G/U$
-invariants and -coinvariants coincide and form exact functors by Maschke’s theorem.
$G/U$
-invariants and -coinvariants coincide and form exact functors by Maschke’s theorem.
Following [Reference Kohlhaase31] we write
![]() $D^\infty (G)$
for the algebra of locally constant distributions, i.e., the quotient of
$D^\infty (G)$
for the algebra of locally constant distributions, i.e., the quotient of
![]() $D(G)$
by the ideal generated by
$D(G)$
by the ideal generated by
![]() $Lie(G)\subseteq D(G).$
We then obtain isomorphisms by [Reference Schneider and Teitelbaum44, p. 306]
$Lie(G)\subseteq D(G).$
We then obtain isomorphisms by [Reference Schneider and Teitelbaum44, p. 306]
where the latter denotes Lie algebra cohomology. Since the reference does not cover coefficient fields such as our K, which is not spherically complete, we would like to briefly justify this isomorphism: For
![]() $Lie(G)=L\nabla $
we have a strict exact sequence of Hausdorff locally convex vector spaces over L
$Lie(G)=L\nabla $
we have a strict exact sequence of Hausdorff locally convex vector spaces over L
by [Reference Schneider and Teitelbaum44, §3], i.e., a resolution of
![]() $D^\infty (G,L)$
by free
$D^\infty (G,L)$
by free
![]() $ D(G,L)$
-modules. Moreover, it arises by base change
$ D(G,L)$
-modules. Moreover, it arises by base change
![]() $D(G,L)\otimes _{U_L(Lie(G))}-$
from the following resolution of L by free
$D(G,L)\otimes _{U_L(Lie(G))}-$
from the following resolution of L by free
![]() $U_L(Lie(G))$
-modules, where the latter denotes the enveloping algebra of
$U_L(Lie(G))$
-modules, where the latter denotes the enveloping algebra of
![]() $Lie(G):$
$Lie(G):$
see [Reference Schneider and Teitelbaum44, Rem. 1.1]. Base change
![]() $K\hat {\otimes }_L-$
of (7) leads to the strict exact sequence of Hausdorff locally convex K-vector spaces
$K\hat {\otimes }_L-$
of (7) leads to the strict exact sequence of Hausdorff locally convex K-vector spaces
by [Reference Schneider and Venjakob46, Lem. 4.3.6]. Since
![]() $K\hat {\otimes }_L D(G,L)\cong D(G,K)$
by the proof of [Reference Schneider and Venjakob46, Lem. 4.1.2], we also obtain
$K\hat {\otimes }_L D(G,L)\cong D(G,K)$
by the proof of [Reference Schneider and Venjakob46, Lem. 4.1.2], we also obtain
![]() $K\hat {\otimes }_L D^\infty (G,L)\cong D^\infty (G,K)$
, i.e., this sequence is the analogue of (7) for K replacing L and visibly it arises again by base change
$K\hat {\otimes }_L D^\infty (G,L)\cong D^\infty (G,K)$
, i.e., this sequence is the analogue of (7) for K replacing L and visibly it arises again by base change
![]() $D(G,K)\otimes _{U_K(Lie(G))}-$
from the analogue of (8)
$D(G,K)\otimes _{U_K(Lie(G))}-$
from the analogue of (8)
Since
![]() $\operatorname {Hom}_{D(G,K)}(D(G,K),V)\cong \operatorname {Hom}_{U_K(Lie(G))}(U_K(Lie(G),V)$
the isomorphism (6) follows.
$\operatorname {Hom}_{D(G,K)}(D(G,K),V)\cong \operatorname {Hom}_{U_K(Lie(G))}(U_K(Lie(G),V)$
the isomorphism (6) follows.
If
![]() $\mathrm {RHom}_{D(G)}(D^\infty (G),V)$
denotes any (bounded) complex of K-vector spaces having the groups (6) as cohomology, we again write
$\mathrm {RHom}_{D(G)}(D^\infty (G),V)$
denotes any (bounded) complex of K-vector spaces having the groups (6) as cohomology, we again write
for the induced mapping fibre.
Assume
![]() $\nabla \in Lie(U)=K$
corresponds to
$\nabla \in Lie(U)=K$
corresponds to
![]() $1.$
Then
$1.$
Then
![]() $V\xrightarrow {\nabla }V$
is a valid (functorial) choice for
$V\xrightarrow {\nabla }V$
is a valid (functorial) choice for
![]() $\mathrm {RHom}_{D(U)}(D^\infty (U),V)$
and we shall also use the notation
$\mathrm {RHom}_{D(U)}(D^\infty (U),V)$
and we shall also use the notation
![]() $K_{f,\nabla }(V)$
instead.
$K_{f,\nabla }(V)$
instead.
Finally, we set
Note that we have isomorphisms (see proof of [Reference Kohlhaase31, Thm. 4.8] or [Reference Weibel56, §10.8.2])
and, for
![]() $G_0\subseteq G$
any L-analytic normal subgroup, (see [Reference Weibel56, Exc. 10.8.5])
$G_0\subseteq G$
any L-analytic normal subgroup, (see [Reference Weibel56, Exc. 10.8.5])
in the derived category, therefore inducing the spectral sequences
and
They both degenerate by the projectivity of K as
![]() $D^\infty (G)$
- and
$D^\infty (G)$
- and
![]() $D(G/G_0)=K[G/G_0]$
-module (cf. the proof of [Reference Kohlhaase31, Thm. 4.10] for the first claim over L, from which the general case again follows by complete base change to K, and using Maschke’s theorem for the second claim). Moreover, note that
$D(G/G_0)=K[G/G_0]$
-module (cf. the proof of [Reference Kohlhaase31, Thm. 4.10] for the first claim over L, from which the general case again follows by complete base change to K, and using Maschke’s theorem for the second claim). Moreover, note that
![]() $\mathrm {Hom}_{D^\infty (G)}(K,W)\cong W^G$
, for any
$\mathrm {Hom}_{D^\infty (G)}(K,W)\cong W^G$
, for any
![]() $D^\infty (G,K)$
-module W, because the Dirac measures
$D^\infty (G,K)$
-module W, because the Dirac measures
![]() $\delta _\gamma \in D^\infty (G,K)$
induce the elements
$\delta _\gamma \in D^\infty (G,K)$
induce the elements
![]() $\delta _\gamma -1$
in the augmentation ideal, which is the kernel of
$\delta _\gamma -1$
in the augmentation ideal, which is the kernel of
![]() $D^\infty (G,K)\twoheadrightarrow K$
and which is a finitely generated ideal by Cor. 4.6 of (loc. cit.) plus complete (exact) base change; using this, the above spectral sequences induce the isomorphisms
$D^\infty (G,K)\twoheadrightarrow K$
and which is a finitely generated ideal by Cor. 4.6 of (loc. cit.) plus complete (exact) base change; using this, the above spectral sequences induce the isomorphisms
and
Remark 4.1. In [Reference Colmez15] the pro-L-locally analytic cohomology groups
![]() $H^i_{an}(A^+,M)$
for the L-analytic semi-group
$H^i_{an}(A^+,M)$
for the L-analytic semi-group
![]() $A^+\cong \Gamma _L\times \{\varphi ^{\mathbb {Z}}\}$
with M being specified below are defined. By [Reference Thomas53, 3.7.6] they are isomorphic to the cohomology groups
$A^+\cong \Gamma _L\times \{\varphi ^{\mathbb {Z}}\}$
with M being specified below are defined. By [Reference Thomas53, 3.7.6] they are isomorphic to the cohomology groups
![]() $H^i_{\varphi _L,\Gamma _L, an}(M)$
which arise as follows: Following [Reference Colmez15, §5] we write
$H^i_{\varphi _L,\Gamma _L, an}(M)$
which arise as follows: Following [Reference Colmez15, §5] we write
![]() $ \mathcal {C}^\bullet _{an}(G,M)$
for the locally L-analytic cochain complex of an L-analytic group G with coefficients in M and
$ \mathcal {C}^\bullet _{an}(G,M)$
for the locally L-analytic cochain complex of an L-analytic group G with coefficients in M and
![]() $H^i_{an}(G,M) := h^i(\mathcal {C}^\bullet _{an}(G,M))$
for locally L-analytic group cohomology. More precisely, let
$H^i_{an}(G,M) := h^i(\mathcal {C}^\bullet _{an}(G,M))$
for locally L-analytic group cohomology. More precisely, let
![]() $M=\varinjlim _s\varprojlim _r M^{[r,s]}$
with Banach spaces
$M=\varinjlim _s\varprojlim _r M^{[r,s]}$
with Banach spaces
![]() $M^{[r,s]} $
be an LF space with a pro-L-analytic action of G (cf. Definition 3.17). If
$M^{[r,s]} $
be an LF space with a pro-L-analytic action of G (cf. Definition 3.17). If
![]() $\mathrm {Maps}_{loc L-an}(G,M^{[r,s]})$
denotes the space of locally L-analytic maps from G to
$\mathrm {Maps}_{loc L-an}(G,M^{[r,s]})$
denotes the space of locally L-analytic maps from G to
![]() $M^{[r,s]}$
, then
$M^{[r,s]}$
, then
is the space of locally L-analytic functions (locally with values in
![]() $\varprojlim _r M^{[r,s]} $
for some s and such that the composite with the projection onto
$\varprojlim _r M^{[r,s]} $
for some s and such that the composite with the projection onto
![]() $M^{[r,s]}$
is locally L-analytic for all r). Then
$M^{[r,s]}$
is locally L-analytic for all r). Then
![]() $H^i_{\varphi _L,G, an}(M):=h^i(K_{\varphi _L,G, an}(M))$
is the cohomology of the mapping fibre
$H^i_{\varphi _L,G, an}(M):=h^i(K_{\varphi _L,G, an}(M))$
is the cohomology of the mapping fibre
![]() $K_{\varphi _L,G,an}(M)$
of
$K_{\varphi _L,G,an}(M)$
of
![]() $\mathcal {C}^\bullet _{an}(G,\varphi _L)$
and analogously for
$\mathcal {C}^\bullet _{an}(G,\varphi _L)$
and analogously for
![]() $\psi $
instead of
$\psi $
instead of
![]() $\varphi _L.$
By [Reference Steingart50, Corollary 4.2.6] we have natural isomorphisms
$\varphi _L.$
By [Reference Steingart50, Corollary 4.2.6] we have natural isomorphisms
and hence, for
![]() $ \clubsuit \in \{\varphi ,\psi \},$
$ \clubsuit \in \{\varphi ,\psi \},$
For
![]() $n \gg 0$
we have that
$n \gg 0$
we have that
![]() $1+\pi _L^n o_L$
is isomorphic to
$1+\pi _L^n o_L$
is isomorphic to
![]() $\pi _L^n o_L$
via
$\pi _L^n o_L$
via
![]() $\log _p$
. In particular, we have the chain of isomorphisms
$\log _p$
. In particular, we have the chain of isomorphisms
which yields
the last isomorphism being the Fourier isomorphism. Since
![]() $\Gamma _n$
is clopen in
$\Gamma _n$
is clopen in
![]() $\Gamma $
, every locally analytic function on
$\Gamma $
, every locally analytic function on
![]() $\Gamma _n$
is the restriction of a locally analytic function on
$\Gamma _n$
is the restriction of a locally analytic function on
![]() $\Gamma _L$
. Hence, by considering the restriction of functions from
$\Gamma _L$
. Hence, by considering the restriction of functions from
![]() $\Gamma _L$
to
$\Gamma _L$
to
![]() $\Gamma _n$
and taking its dual, we obtain an injective map
$\Gamma _n$
and taking its dual, we obtain an injective map ![]() .
.
Definition 4.2. For
![]() $n\gg 0$
such that
$n\gg 0$
such that
![]() $\Gamma _n = \operatorname {Gal}(L_\infty /L_n)\cong o_L$
we denote by
$\Gamma _n = \operatorname {Gal}(L_\infty /L_n)\cong o_L$
we denote by
![]() ${\mathfrak {Z}_n \in D(\Gamma _n,K)\cong \mathcal {R}_K^+}$
the element corresponding to
${\mathfrak {Z}_n \in D(\Gamma _n,K)\cong \mathcal {R}_K^+}$
the element corresponding to
![]() $Z \in \mathcal {R}_K^+.$
If the precise choice of n is not relevant, we frequently write
$Z \in \mathcal {R}_K^+.$
If the precise choice of n is not relevant, we frequently write
![]() $(U,\mathfrak {Z})$
instead of
$(U,\mathfrak {Z})$
instead of
![]() $(\Gamma _n,\mathfrak {Z}_n).$
$(\Gamma _n,\mathfrak {Z}_n).$
Remark 4.3. Let
![]() $n \gg 0$
such that
$n \gg 0$
such that
![]() $\Gamma _n \cong o_L.$
Under the natural inclusions
$\Gamma _n \cong o_L.$
Under the natural inclusions
![]() $D(\Gamma _{n+1},K) \subseteq D(\Gamma _n,K)$
and
$D(\Gamma _{n+1},K) \subseteq D(\Gamma _n,K)$
and
![]() $\operatorname {Lie}(\Gamma _L)=\operatorname {Lie}(\Gamma _n) \subseteq D(\Gamma _n,K)$
we have:
$\operatorname {Lie}(\Gamma _L)=\operatorname {Lie}(\Gamma _n) \subseteq D(\Gamma _n,K)$
we have:
-
(i)
 $\mathfrak {Z}_{n+1} = [\pi _L](\mathfrak {Z}_n)$
in the ring
$\mathfrak {Z}_{n+1} = [\pi _L](\mathfrak {Z}_n)$
in the ring
 $D(\Gamma _n,K).$
$D(\Gamma _n,K).$
-
(ii)
 $\nabla = \frac {\Omega }{\pi _L^n} \log _{LT}(\mathfrak {Z}_n)$
in
$\nabla = \frac {\Omega }{\pi _L^n} \log _{LT}(\mathfrak {Z}_n)$
in
 $D(\Gamma _n,K).$
In particular,
$D(\Gamma _n,K).$
In particular,
 $\nabla $
is divisible by
$\nabla $
is divisible by
 $\mathfrak {Z}_n.$
$\mathfrak {Z}_n.$
Proof. For (i) see [Reference Steingart50, Definition 1.2.10]. For (ii) see (the proof of) [Reference Schneider and Venjakob46, Remark 4.4.8].
Lemma 4.4. Let A be K-affinoid and let
![]() $M \in \mathfrak {M}^{an}(\mathcal {R}_A).$
Then:
$M \in \mathfrak {M}^{an}(\mathcal {R}_A).$
Then:
-
(i) For
 $r \in (0,1)$
large enough the action of
$r \in (0,1)$
large enough the action of
 $\mathfrak {Z}$
on
$\mathfrak {Z}$
on
 $(M^{r})^{\psi =0}$
is invertible.
$(M^{r})^{\psi =0}$
is invertible. -
(ii) The action of
 $\mathfrak {Z}$
on
$\mathfrak {Z}$
on
 $M^{\psi =0}$
is invertible.
$M^{\psi =0}$
is invertible. -
(iii) Analogous results hold for M (resp.
 $M^r$
) replaced by
$M^r$
) replaced by
 $M_{t_{LT}}$
(resp.
$M_{t_{LT}}$
(resp.
 $M^r_{t_{LT}}).$
$M^r_{t_{LT}}).$
Proof. The case
![]() $A=K$
is originally treated in [Reference Schneider and Venjakob46, Theorem 4.3.21]. For (i) in the general case see [Reference Steingart50, Theorem 2.4.5]. The second point follows by passing to the colimit. The third point also follows by passing to the colimit, where for
$A=K$
is originally treated in [Reference Schneider and Venjakob46, Theorem 4.3.21]. For (i) in the general case see [Reference Steingart50, Theorem 2.4.5]. The second point follows by passing to the colimit. The third point also follows by passing to the colimit, where for
![]() $mt_{LT}^{-k} \in Mt_{LT}^{-k}$
one extends
$mt_{LT}^{-k} \in Mt_{LT}^{-k}$
one extends
![]() $\psi $
by setting
$\psi $
by setting
![]() $\psi (mt_{LT}^{-k}):=\pi _L^{k}\psi (m)t_{LT}^{-k}$
(cf. [Reference Schneider and Venjakob46, Lemma 4.5.23] for details in the case
$\psi (mt_{LT}^{-k}):=\pi _L^{k}\psi (m)t_{LT}^{-k}$
(cf. [Reference Schneider and Venjakob46, Lemma 4.5.23] for details in the case
![]() $A=K$
).
$A=K$
).
Lemma 4.5.
-
(i)
 $H^i_{\clubsuit ,\spadesuit }(V)=0$
for
$H^i_{\clubsuit ,\spadesuit }(V)=0$
for
 $i\neq 0,1,2.$
$i\neq 0,1,2.$
-
(ii)
 $H^\bullet _{\varphi ,D(G)}(M) \cong H^\bullet _{\varphi ,Lie(G)}(M)^{ G }$
for M in
$H^\bullet _{\varphi ,D(G)}(M) \cong H^\bullet _{\varphi ,Lie(G)}(M)^{ G }$
for M in
 $\mathfrak {M}^{an}(\mathcal {R})$
.Footnote
7
$\mathfrak {M}^{an}(\mathcal {R})$
.Footnote
7
-
(iii)
 $H^\bullet _{\varphi ,D(G)}(M)\cong H^\bullet _{\Psi ,D(G)}(M)$
for M in
$H^\bullet _{\varphi ,D(G)}(M)\cong H^\bullet _{\Psi ,D(G)}(M)$
for M in
 $\mathfrak {M}^{an}(\mathcal {R})$
.Footnote
8
$\mathfrak {M}^{an}(\mathcal {R})$
.Footnote
8
Proof. Part (i) holds due to the length of the total complex. (ii) follows immediately from (11) upon considering one of the spectral sequences attached to the double complexes arising from the defining mapping fibres. By (12), (iii) is reduced to the case
![]() $H^\bullet _{\varphi ,{\mathfrak {Z}}}(M)\cong H^\bullet _{\Psi ,{\mathfrak {Z}}}(M)$
, which is a consequence of Lemma 4.4.
$H^\bullet _{\varphi ,{\mathfrak {Z}}}(M)\cong H^\bullet _{\Psi ,{\mathfrak {Z}}}(M)$
, which is a consequence of Lemma 4.4.
4.1 Finiteness of analytic Cohomology
Theorem 4.6. Let
![]() $A,B$
be K-affinoid and let M be an L-analytic
$A,B$
be K-affinoid and let M be an L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_A.$
Let
$\mathcal {R}_A.$
Let
![]() $f\colon A \to B$
be a morphism of K-affinoid algebras. Then:
$f\colon A \to B$
be a morphism of K-affinoid algebras. Then:
-
(1)
 $K_{\varphi _L,\mathfrak {Z}}(M) \in \mathbf {D}^{[0,2]}_{\mathrm {perf}}(A).$
$K_{\varphi _L,\mathfrak {Z}}(M) \in \mathbf {D}^{[0,2]}_{\mathrm {perf}}(A).$
-
(2) The natural morphism
 $K_{\varphi _L,\mathfrak {Z}}(M) \otimes _{A}^{\mathbb {L}} B \to K_{\varphi _L,\mathfrak {Z}}(M \hat {\otimes }_A B)$
is a quasi-isomorphism.
$K_{\varphi _L,\mathfrak {Z}}(M) \otimes _{A}^{\mathbb {L}} B \to K_{\varphi _L,\mathfrak {Z}}(M \hat {\otimes }_A B)$
is a quasi-isomorphism.
Proof. See [Reference Steingart50, Theorem 3.3.12].
For a commutative ring R and an object
![]() $C \in \mathbf {D}^b(R)$
whose cohomology groups are of finite rank over
$C \in \mathbf {D}^b(R)$
whose cohomology groups are of finite rank over
![]() $R,$
we denote by
$R,$
we denote by
![]() $\chi _R(C) = \sum _i (-1)^i \operatorname {rank}H^i(C)$
the Euler-Poincaré-characteristic of
$\chi _R(C) = \sum _i (-1)^i \operatorname {rank}H^i(C)$
the Euler-Poincaré-characteristic of
![]() $C.$
Recall that a
$C.$
Recall that a
![]() $(\varphi _L,\Gamma _L)$
-module is called trianguline if it can be written as a successive extension of rank one modules of character type in the sense of section 3.4.
$(\varphi _L,\Gamma _L)$
-module is called trianguline if it can be written as a successive extension of rank one modules of character type in the sense of section 3.4.
Remark 4.7. Let
![]() $A/K$
be affinoid and let
$A/K$
be affinoid and let
![]() $M $
be a trianguline L-analytic
$M $
be a trianguline L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_A.$
Then the Euler-Poincaré Formula holds, i.e.,
$\mathcal {R}_A.$
Then the Euler-Poincaré Formula holds, i.e.,
Proof. Without loss of generality we may assume that
![]() $M = \mathcal {R}_A(\delta )$
is an L-analytic module of character type (attached to an A-valued locally L-analytic character
$M = \mathcal {R}_A(\delta )$
is an L-analytic module of character type (attached to an A-valued locally L-analytic character
![]() $\delta \colon L^\times \to A^\times ).$
Then the case
$\delta \colon L^\times \to A^\times ).$
Then the case
![]() $A=K$
is treated in [Reference Steingart51, Remark 6.3]. The validity of the formula can be checked at each maximal ideal of
$A=K$
is treated in [Reference Steingart51, Remark 6.3]. The validity of the formula can be checked at each maximal ideal of
![]() $A.$
Note that
$A.$
Note that
![]() $\mathcal {R}_A(\delta )/\mathfrak {m}$
is a
$\mathcal {R}_A(\delta )/\mathfrak {m}$
is a
![]() $(\varphi _L,\Gamma _L)$
-module of character type over
$(\varphi _L,\Gamma _L)$
-module of character type over
![]() $\mathcal {R}_{K'}$
for some finite extension
$\mathcal {R}_{K'}$
for some finite extension
![]() $K'/K$
for each
$K'/K$
for each
![]() $\mathfrak {m} \in \operatorname {\mathrm {Max}}(A)$
by the Nullstellensatz and the claim hence follows from the previous case.
$\mathfrak {m} \in \operatorname {\mathrm {Max}}(A)$
by the Nullstellensatz and the claim hence follows from the previous case.
We will require a slight generalization of 4.6. Recall that
![]() $K_{\varphi _L,\mathfrak {Z}}(M)$
is (up to shift) quasi isomorphic to the cone of
$K_{\varphi _L,\mathfrak {Z}}(M)$
is (up to shift) quasi isomorphic to the cone of
![]() $1-\varphi $
on
$1-\varphi $
on
![]() $\operatorname {RHom}_{D(U,K)}(K,M).$
As a consequence of [Reference Steingart51, Lemma 2.5] K admits a finite projective resolution consisting of finitely generated projective
$\operatorname {RHom}_{D(U,K)}(K,M).$
As a consequence of [Reference Steingart51, Lemma 2.5] K admits a finite projective resolution consisting of finitely generated projective
![]() $D(\Gamma _L,K)$
-modules. In particular the complex computing
$D(\Gamma _L,K)$
-modules. In particular the complex computing
![]() $\operatorname {RHom}_{D(U,K)}(K,M)$
(and hence also
$\operatorname {RHom}_{D(U,K)}(K,M)$
(and hence also
![]() $K_{\varphi _L,\mathfrak {Z}}(M)$
) can be represented by a complex of
$K_{\varphi _L,\mathfrak {Z}}(M)$
) can be represented by a complex of
![]() $A[\Gamma _L/U]$
-modules the terms of which are all of the form
$A[\Gamma _L/U]$
-modules the terms of which are all of the form
![]() $\operatorname {Hom}_{D(U,K)}(P,M),$
where P is the restriction of scalars of a projective
$\operatorname {Hom}_{D(U,K)}(P,M),$
where P is the restriction of scalars of a projective
![]() $D(\Gamma _L,K)$
-module with
$D(\Gamma _L,K)$
-module with
![]() $\Gamma _L$
acting via
$\Gamma _L$
acting via
![]() $(\gamma f)(x) = \gamma (f(\gamma ^{-1}x))$
and A acting by multiplication on
$(\gamma f)(x) = \gamma (f(\gamma ^{-1}x))$
and A acting by multiplication on
![]() $M.$
$M.$
Remark 4.8. In the situation of 4.6, if we view
![]() $K_{\varphi _L,{\mathfrak {Z}}}(M)$
as an object in
$K_{\varphi _L,{\mathfrak {Z}}}(M)$
as an object in
![]() $\mathbf {D}(A[\Gamma _L/U])$
we have
$\mathbf {D}(A[\Gamma _L/U])$
we have
Proof. The finiteness of the cohomology groups over A already implies that
![]() $K_{\varphi _L,\mathfrak {Z}}(M)$
belongs to
$K_{\varphi _L,\mathfrak {Z}}(M)$
belongs to
![]() $ \mathbf {D}^{-}_{\mathrm {perf}}(A[\Gamma _L/U]).$
Choosing a complex of bounded above projective
$ \mathbf {D}^{-}_{\mathrm {perf}}(A[\Gamma _L/U]).$
Choosing a complex of bounded above projective
![]() $A[\Gamma _L/U]$
-modules representing
$A[\Gamma _L/U]$
-modules representing
![]() $K_{\varphi _L,\mathfrak {Z}}(M)$
, truncating and using [Reference Kedlaya, Pottharst and Xiao28, Lemma 4.1.3], we can conclude that the complex in question is quasi isomorphic to a bounded complex of finitely generated projectives outside of perhaps degree
$K_{\varphi _L,\mathfrak {Z}}(M)$
, truncating and using [Reference Kedlaya, Pottharst and Xiao28, Lemma 4.1.3], we can conclude that the complex in question is quasi isomorphic to a bounded complex of finitely generated projectives outside of perhaps degree
![]() $0,$
where the module is finitely generated over
$0,$
where the module is finitely generated over
![]() $A[\Gamma _L/U]$
and its underlying A-module is flat. But then it is projective as an A-module and by [Reference Steingart51, Lemma 2.5] also projective as an
$A[\Gamma _L/U]$
and its underlying A-module is flat. But then it is projective as an A-module and by [Reference Steingart51, Lemma 2.5] also projective as an
![]() $A[\Gamma _L/U]$
-module, hence the claim.
$A[\Gamma _L/U]$
-module, hence the claim.
4.2 Perfectness of analytic Iwasawa cohomology and the Lubin-Tate deformation
For M any
![]() $(\varphi _L,\Gamma _L)$
-module over any basis consider the complex
$(\varphi _L,\Gamma _L)$
-module over any basis consider the complex
concentrated in degrees
![]() $1$
and
$1$
and
![]() $2$
, whose cohomology we call (analytic) Iwasawa cohomology due to Fontaine’s classical result, which relates these groups in the étale case to usual Iwasawa cohomology defined in terms of Galois cohomology. We set
$2$
, whose cohomology we call (analytic) Iwasawa cohomology due to Fontaine’s classical result, which relates these groups in the étale case to usual Iwasawa cohomology defined in terms of Galois cohomology. We set
![]() $D:=D(\Gamma _L,K).$
The following result [Reference Steingart51, Thm. 4.8] will be central for the whole article:
$D:=D(\Gamma _L,K).$
The following result [Reference Steingart51, Thm. 4.8] will be central for the whole article:
Theorem 4.9. For
![]() $M\in \mathfrak {M}^{an}(K)$
trianguline,
$M\in \mathfrak {M}^{an}(K)$
trianguline,
![]() $\mathcal {T}_{\Psi }(M) $
is a perfect complex of D-modules, i.e., belongs to
$\mathcal {T}_{\Psi }(M) $
is a perfect complex of D-modules, i.e., belongs to
![]() $\mathbf {D}^b_{\mathrm {perf}}(D)$
.
$\mathbf {D}^b_{\mathrm {perf}}(D)$
.
For the rest of this subsection we assume that
![]() $M\in \mathfrak {M}^{an}(K)$
is trianguline.
$M\in \mathfrak {M}^{an}(K)$
is trianguline.
Later for our approach it will be important to interpret Iwasawa cohomology as analytic cohomology of a deformation
![]() $\mathbf {Dfm}(M)$
of M via generalized Herr complexes. This deformation lives over the character variety
$\mathbf {Dfm}(M)$
of M via generalized Herr complexes. This deformation lives over the character variety
![]() $\mathfrak {X}_{\Gamma _L}$
(base changed to K) of the locally L-analytic group
$\mathfrak {X}_{\Gamma _L}$
(base changed to K) of the locally L-analytic group
![]() $\Gamma _L$
([Reference Schneider and Teitelbaum42]) and will allow to use density arguments to deduce many properties of the Epsilon-isomorphism for rank one modules just from properties over its de Rham points.
$\Gamma _L$
([Reference Schneider and Teitelbaum42]) and will allow to use density arguments to deduce many properties of the Epsilon-isomorphism for rank one modules just from properties over its de Rham points.
We pick an affinoid cover
![]() $X_n\cong \operatorname {Sp}(D_n)$
of
$X_n\cong \operatorname {Sp}(D_n)$
of
![]() $\mathfrak {X}_{\Gamma _L}$
with
$\mathfrak {X}_{\Gamma _L}$
with
![]() $D_n:=K[\Gamma _L]\otimes _{K[U]}D_{r_n}(U,K)$
for a decreasing sequence
$D_n:=K[\Gamma _L]\otimes _{K[U]}D_{r_n}(U,K)$
for a decreasing sequence
![]() $r_n$
such that each
$r_n$
such that each
![]() $D_{r_n}(U,K) $
corresponds to the ring of rigid analytic functions on the annulus
$D_{r_n}(U,K) $
corresponds to the ring of rigid analytic functions on the annulus
![]() $[r_n,\infty ]$
via the Fourier isomorphism for
$[r_n,\infty ]$
via the Fourier isomorphism for
![]() $D(U,K)$
. Over the space
$D(U,K)$
. Over the space
![]() $\mathfrak {X}_{\Gamma _L}$
we have the sheaf of Robba rings
$\mathfrak {X}_{\Gamma _L}$
we have the sheaf of Robba rings
![]() $\mathcal {R}_{\mathfrak {X}_{\Gamma _L}}$
given by mapping
$\mathcal {R}_{\mathfrak {X}_{\Gamma _L}}$
given by mapping
![]() $X_n$
to
$X_n$
to
![]() $\mathcal {R}_{\mathcal {O}_{\mathfrak {X}_{\Gamma _L}}(X_n)}$
and
$\mathcal {R}_{\mathcal {O}_{\mathfrak {X}_{\Gamma _L}}(X_n)}$
and
![]() $\mathbf {Dfm}(M)$
should be thought of as a
$\mathbf {Dfm}(M)$
should be thought of as a
![]() $(\varphi _L, \Gamma _L)$
-module (sheaf) over
$(\varphi _L, \Gamma _L)$
-module (sheaf) over
![]() $\mathcal {R}_{\mathfrak {X}_{\Gamma _L}}$
(but unfortunately, Schneider’s and Teitelbaum’s formalism of coadmissible modules does not apply here as
$\mathcal {R}_{\mathfrak {X}_{\Gamma _L}}$
(but unfortunately, Schneider’s and Teitelbaum’s formalism of coadmissible modules does not apply here as
![]() $\mathcal {R}_{\mathfrak {X}_{\Gamma _L}}(\mathfrak {X}_{\Gamma _L})$
does not form a Fréchet-Stein algebra in any obvious sense):
$\mathcal {R}_{\mathfrak {X}_{\Gamma _L}}(\mathfrak {X}_{\Gamma _L})$
does not form a Fréchet-Stein algebra in any obvious sense):
For an L-analytic
![]() $(\varphi ,\Gamma _L)$
-module M over
$(\varphi ,\Gamma _L)$
-module M over
![]() $\mathcal {R}_L$
we define
$\mathcal {R}_L$
we define
where
![]() $\Gamma _L$
acts diagonally, on the left factor via the inversion and on M via its given action. For each n this is a
$\Gamma _L$
acts diagonally, on the left factor via the inversion and on M via its given action. For each n this is a
![]() $(\varphi ,\Gamma _L)$
-module M over
$(\varphi ,\Gamma _L)$
-module M over
![]() $\mathcal {R}_{\mathcal {O}_{\mathfrak {X}_{\Gamma _L}}(X_n)}$
by [Reference Steingart51, Prop. 3.2].
$\mathcal {R}_{\mathcal {O}_{\mathfrak {X}_{\Gamma _L}}(X_n)}$
by [Reference Steingart51, Prop. 3.2].
As definition for the generalized Herr complex for the sheaf
![]() $\mathbf {Dfm}(M)$
, philosophically, we would like to take the complex in
$\mathbf {Dfm}(M)$
, philosophically, we would like to take the complex in
![]() $\mathbf {D}(D(\Gamma _L,K))$
Footnote
9
defined as total derived sheaf cohomology of the complex of sheaves
$\mathbf {D}(D(\Gamma _L,K))$
Footnote
9
defined as total derived sheaf cohomology of the complex of sheaves
where for the last (quasi-)isomorphism in quotation marks we used implicitly the free resolution
which induces an isomorphism
![]() $\mathcal {T}_{\Psi }(\mathbf {Dfm}(M))\otimes ^{\mathbb {L}}_{D(\Gamma _L,K),\mathrm {diag}}K[\Gamma _L/U]\cong K_{\Psi ,{\mathfrak {Z}}}(\mathbf {Dfm}(M)).$
$\mathcal {T}_{\Psi }(\mathbf {Dfm}(M))\otimes ^{\mathbb {L}}_{D(\Gamma _L,K),\mathrm {diag}}K[\Gamma _L/U]\cong K_{\Psi ,{\mathfrak {Z}}}(\mathbf {Dfm}(M)).$
But strictly speaking one needs a resolution of
![]() $D(\Gamma _L,K)\otimes _K K[\Gamma _L/U]$
-modules in order to define the
$D(\Gamma _L,K)\otimes _K K[\Gamma _L/U]$
-modules in order to define the
![]() $(D_n,K[\Gamma _L/U])$
-bimodule structure on
$(D_n,K[\Gamma _L/U])$
-bimodule structure on
![]() $K_{\Psi ,{\mathfrak {Z}}}(\mathbf {Dfm}_n(M))\cong \mathcal {T}_{\Psi }(\mathbf {Dfm}_n(M))\otimes ^{\mathbb {L}}_{D(\Gamma _L,K)}K[\Gamma _L/U]$
. To this end we can formally work with the resolution
$K_{\Psi ,{\mathfrak {Z}}}(\mathbf {Dfm}_n(M))\cong \mathcal {T}_{\Psi }(\mathbf {Dfm}_n(M))\otimes ^{\mathbb {L}}_{D(\Gamma _L,K)}K[\Gamma _L/U]$
. To this end we can formally work with the resolution
for an explicit construction of
![]() $K_{\Psi ,{\mathfrak {Z}}}(\mathbf {Dfm}(M))$
in
$K_{\Psi ,{\mathfrak {Z}}}(\mathbf {Dfm}(M))$
in
![]() $\mathbf {D}((D_n,K[\Gamma _L/U])\mathrm {-bimod}),$
with the last non-trivial map given by
$\mathbf {D}((D_n,K[\Gamma _L/U])\mathrm {-bimod}),$
with the last non-trivial map given by
![]() $a\otimes b\mapsto H(a)\cdot b,$
where
$a\otimes b\mapsto H(a)\cdot b,$
where
![]() $H\colon D(\Gamma _L,K)\to K[\Gamma _L/U]$
denotes the augmentation map sending the Dirac distributions of
$H\colon D(\Gamma _L,K)\to K[\Gamma _L/U]$
denotes the augmentation map sending the Dirac distributions of
![]() $u\in U$
to
$u\in U$
to
![]() $1.$
Indeed, the kernel C is projective (hence flat) as a D-module by the same reasoning as for [Reference Steingart51, Lem. 2.5]. This sequence is related to (the direct sum of) the sequences
$1.$
Indeed, the kernel C is projective (hence flat) as a D-module by the same reasoning as for [Reference Steingart51, Lem. 2.5]. This sequence is related to (the direct sum of) the sequences
for the characters
![]() $\chi _i$
of
$\chi _i$
of
![]() $\Gamma _L$
which factor through
$\Gamma _L$
which factor through
![]() $\Gamma _L/U.$
$\Gamma _L/U.$
Instead of verifying that we really have a complex of (coherent) sheaves we just use the facts as a motivation that on a Stein space
![]() $\Gamma (\mathfrak {X}_{\Gamma _L},-)=\varprojlim _n \Gamma (X_n,-)$
and that higher sheaf cohomology of coherent sheaves vanishes on affinoids. Thus we rather take the total derived inverse limit as a formal definition, i.e.,
$\Gamma (\mathfrak {X}_{\Gamma _L},-)=\varprojlim _n \Gamma (X_n,-)$
and that higher sheaf cohomology of coherent sheaves vanishes on affinoids. Thus we rather take the total derived inverse limit as a formal definition, i.e.,
The following results are variants of those in [Reference Steingart51, §3.3]; among others they are based on the observation that for the sheaf of cohomology groups sending
![]() $X_n$
to
$X_n$
to
![]() $H^i_{\Psi , D(\Gamma _L,K)}(\mathbf {Dfm}_n(M))$
the formalism of coadmissible modules over
$H^i_{\Psi , D(\Gamma _L,K)}(\mathbf {Dfm}_n(M))$
the formalism of coadmissible modules over
![]() $D(\Gamma _L,K)$
does apply.
$D(\Gamma _L,K)$
does apply.
Theorem 4.10.
-
(i) For all i, the cohomology groups
 $H^i_{\Psi ,D(\Gamma _L,K)}(\mathfrak {X}_{\Gamma _L}, \mathbf {Dfm}(M))$
of the complex
$H^i_{\Psi ,D(\Gamma _L,K)}(\mathfrak {X}_{\Gamma _L}, \mathbf {Dfm}(M))$
of the complex
 $R\Gamma _{\Psi ,D(\Gamma _L,K)}(\mathfrak {X}_{\Gamma _L}, \mathbf {Dfm}(M)) $
coincide with the global sections of the sheaf of cohomology groups sending
$R\Gamma _{\Psi ,D(\Gamma _L,K)}(\mathfrak {X}_{\Gamma _L}, \mathbf {Dfm}(M)) $
coincide with the global sections of the sheaf of cohomology groups sending $$\begin{align*}\varprojlim_n H^i_{\Psi,D(\Gamma_L,K)}(\mathbf{Dfm}_n(M))\end{align*}$$
$$\begin{align*}\varprojlim_n H^i_{\Psi,D(\Gamma_L,K)}(\mathbf{Dfm}_n(M))\end{align*}$$
 $X_n$
to
$X_n$
to
 $H^i_{\Psi , D(\Gamma _L,K)}(\mathbf {Dfm}_n(M)). $
$H^i_{\Psi , D(\Gamma _L,K)}(\mathbf {Dfm}_n(M)). $
-
(ii) There is an isomorphism in
 $\mathbf {D}^b_{\mathrm {perf}}(D(\Gamma _L,K))$
$\mathbf {D}^b_{\mathrm {perf}}(D(\Gamma _L,K))$
 $$\begin{align*}R\Gamma_{\Psi,D(\Gamma_L,K)}(\mathfrak{X}_{\Gamma_L}, \mathbf{Dfm}(M))\cong \mathcal{T}_{\Psi}(M).\end{align*}$$
$$\begin{align*}R\Gamma_{\Psi,D(\Gamma_L,K)}(\mathfrak{X}_{\Gamma_L}, \mathbf{Dfm}(M))\cong \mathcal{T}_{\Psi}(M).\end{align*}$$
Remark 4.11. In accordance with (21) the isomorphism in (ii) only becomes independent of the choice of
![]() ${\mathfrak {Z}}$
if we insert the scalar factor
${\mathfrak {Z}}$
if we insert the scalar factor
![]() $C_{Tr}({{\mathfrak {Z}}_n})$
(see (20) below) in the identification
$C_{Tr}({{\mathfrak {Z}}_n})$
(see (20) below) in the identification
![]() $ \mathbf {Dfm}_n(M)/{\mathfrak {Z}}\mathbf {Dfm}_n(M)\cong D_n\tilde {\otimes }_{D(U,K)}M$
in the proof of Lemma 4.12, compare with [Reference Nakamura36, (32), p. 369].
$ \mathbf {Dfm}_n(M)/{\mathfrak {Z}}\mathbf {Dfm}_n(M)\cong D_n\tilde {\otimes }_{D(U,K)}M$
in the proof of Lemma 4.12, compare with [Reference Nakamura36, (32), p. 369].
For the proof of Theorem 4.10 we need the following lemma for which we recall some notation from [Reference Steingart51, Def. 3.20]: We define
![]() $D_n\hat {\otimes }_D M^r$
as the completion of
$D_n\hat {\otimes }_D M^r$
as the completion of
![]() $D_n\otimes _D M^r$
with respect to the quotient topology of the projective tensor product
$D_n\otimes _D M^r$
with respect to the quotient topology of the projective tensor product
![]() $D_n\otimes _{K,\pi }M^r$
. Then we set
$D_n\otimes _{K,\pi }M^r$
. Then we set
![]() $D_n\tilde {\otimes }_D M:=\varinjlim _r D_n\hat {\otimes }_D M^r.$
$D_n\tilde {\otimes }_D M:=\varinjlim _r D_n\hat {\otimes }_D M^r.$
Lemma 4.12.
-
(i) The natural map
 $D_n\otimes _D M\to D_n\tilde {\otimes }_D M$
induces a quasi-isomorphism
$D_n\otimes _D M\to D_n\tilde {\otimes }_D M$
induces a quasi-isomorphism  $$\begin{align*}D_n\otimes_D \mathcal{T}_\Psi(M)=\mathcal{T}_\Psi(D_n\otimes_D M)\to \mathcal{T}_\Psi(D_n\tilde{\otimes}_D M).\end{align*}$$
$$\begin{align*}D_n\otimes_D \mathcal{T}_\Psi(M)=\mathcal{T}_\Psi(D_n\otimes_D M)\to \mathcal{T}_\Psi(D_n\tilde{\otimes}_D M).\end{align*}$$
-
(ii) Viewing
 $\mathbf {Dfm}_n(M)$
as
$\mathbf {Dfm}_n(M)$
as
 $D_n$
-module via the left tensor factor, there is a natural isomorphism in
$D_n$
-module via the left tensor factor, there is a natural isomorphism in
 $\mathbf {D}(D_n)$
where the latter module is considered as complex concentrated in degree
$\mathbf {D}(D_n)$
where the latter module is considered as complex concentrated in degree $$\begin{align*}\mathbf{Dfm}_n(M) \otimes^{\mathbb{L}}_{D(\Gamma_L,K),\mathrm{diag}}K\cong D_n\tilde{\otimes}_{D}M[0],\end{align*}$$
$$\begin{align*}\mathbf{Dfm}_n(M) \otimes^{\mathbb{L}}_{D(\Gamma_L,K),\mathrm{diag}}K\cong D_n\tilde{\otimes}_{D}M[0],\end{align*}$$
 $0.$
$0.$
Proof. For (i) the same proof as for [Reference Steingart51, Lem. 3.23] works and the assumptions are satisfied by Theorem 4.9, but note that there
![]() $D_n$
, D have a slightly different meaning. The augmentation ideal
$D_n$
, D have a slightly different meaning. The augmentation ideal
![]() $I_{\Gamma _L}$
is a finitely generated submodule of
$I_{\Gamma _L}$
is a finitely generated submodule of
![]() $D(\Gamma _L,K)$
and thus projective as a
$D(\Gamma _L,K)$
and thus projective as a
![]() $D(U,K)$
-module since the latter is a Prüfer Domain. Using [Reference Steingart51, Lemma 2.5] one can conclude projectivity as a
$D(U,K)$
-module since the latter is a Prüfer Domain. Using [Reference Steingart51, Lemma 2.5] one can conclude projectivity as a
![]() $D(\Gamma _L,K)$
-module. Using that
$D(\Gamma _L,K)$
-module. Using that
![]() $D{\mathfrak {Z}}$
is contained in
$D{\mathfrak {Z}}$
is contained in
![]() $I_{\Gamma _L}$
gives rise to the projective resolution of D-modules
$I_{\Gamma _L}$
gives rise to the projective resolution of D-modules
We can represent the complex in question in (ii) by the complex
with cokernel
 $$ \begin{align*} \mathbf{Dfm}_n(M)/I_{\Gamma_L}\mathbf{Dfm}_n(M)&\cong (\mathbf{Dfm}_n(M)/{\mathfrak{Z}}\mathbf{Dfm}_n(M))/(I_{\Gamma_L}/D{\mathfrak{Z}})\\ &=(D_n\tilde{\otimes}_{D(U,K)}M)_{\Gamma_L/U}\\ &=D_n \tilde{\otimes}_DM, \end{align*} $$
$$ \begin{align*} \mathbf{Dfm}_n(M)/I_{\Gamma_L}\mathbf{Dfm}_n(M)&\cong (\mathbf{Dfm}_n(M)/{\mathfrak{Z}}\mathbf{Dfm}_n(M))/(I_{\Gamma_L}/D{\mathfrak{Z}})\\ &=(D_n\tilde{\otimes}_{D(U,K)}M)_{\Gamma_L/U}\\ &=D_n \tilde{\otimes}_DM, \end{align*} $$
where
![]() $ \gamma \in \Gamma _L\subseteq D(\Gamma _L,K)$
acts diagonally (via
$ \gamma \in \Gamma _L\subseteq D(\Gamma _L,K)$
acts diagonally (via
![]() $\gamma (a \otimes b) = \delta _{\gamma ^{-1}} a \otimes \gamma b)$
) on
$\gamma (a \otimes b) = \delta _{\gamma ^{-1}} a \otimes \gamma b)$
) on
![]() $D_n\tilde {\otimes }_{D(U,K)}M$
and this action factors over
$D_n\tilde {\otimes }_{D(U,K)}M$
and this action factors over
![]() $\Gamma _L/U$
. For the second equality we use an obvious variant of [Reference Steingart51, (31)], while by the exactness of colimits the last one is easily reduced to the claim that on the level of models
$\Gamma _L/U$
. For the second equality we use an obvious variant of [Reference Steingart51, (31)], while by the exactness of colimits the last one is easily reduced to the claim that on the level of models
![]() $M^r$
we have
$M^r$
we have
Since
![]() $\Gamma /U$
is finite and taking
$\Gamma /U$
is finite and taking
![]() $\Gamma _L/U$
-invariants in this situation is exact by Maschke’s theorem, this follows in the context of Fréchet spaces by completion from the well-known fact that
$\Gamma _L/U$
-invariants in this situation is exact by Maschke’s theorem, this follows in the context of Fréchet spaces by completion from the well-known fact that
The injectivity of the non-trivial differential in the above complex can be checked by calculating instead the cohomology in degree
![]() $-1$
of
$-1$
of
![]() $\mathbf {Dfm}_n(M) \otimes ^{\mathbb {L}}_{D(\Gamma _L,K),\mathrm {diag}}K[\Gamma _L/U]$
, because taking
$\mathbf {Dfm}_n(M) \otimes ^{\mathbb {L}}_{D(\Gamma _L,K),\mathrm {diag}}K[\Gamma _L/U]$
, because taking
![]() $\Gamma _L/U$
-(co)invariants is exact and leads to the original complex
$\Gamma _L/U$
-(co)invariants is exact and leads to the original complex
For this composition of functors it is crucial that
![]() $\mathbf {Dfm}_n(M) \otimes ^{\mathbb {L}}_{D(\Gamma _L,K),\mathrm {diag}}K[\Gamma _L/U]$
belongs to
$\mathbf {Dfm}_n(M) \otimes ^{\mathbb {L}}_{D(\Gamma _L,K),\mathrm {diag}}K[\Gamma _L/U]$
belongs to
![]() $\mathbf {D}((D_n,K[\Gamma _L/U])\mathrm {-bimod})$
as in (18) in order to allow an action by
$\mathbf {D}((D_n,K[\Gamma _L/U])\mathrm {-bimod})$
as in (18) in order to allow an action by
![]() $\Gamma _L/U$
. But then the vanishing in degree
$\Gamma _L/U$
. But then the vanishing in degree
![]() $-1$
can be checked just as complex of K-vector spaces and therefore it suffices to calculate the derived functor by a projective resolution of D-modules (instead of bi-modules). To this end we use the resolution (17), which leads to the complex
$-1$
can be checked just as complex of K-vector spaces and therefore it suffices to calculate the derived functor by a projective resolution of D-modules (instead of bi-modules). To this end we use the resolution (17), which leads to the complex
which is left exact by an obvious variant of [Reference Steingart51, (31)], again.
Proof of Theorem 4.10
Using Lemma 4.12 we obtain isomorphisms in
![]() $\mathbf {D}(D_n)$
$\mathbf {D}(D_n)$
 $$ \begin{align*} K_{\Psi,D(\Gamma_L,K)}&(\mathbf{Dfm}_n(M))\\ & \cong \mathrm{cone} \big( \mathbf{Dfm}_n(M)\otimes^{\mathbb{L}}_{D(\Gamma_L,K),\mathrm{diag}}K\xrightarrow{\Psi-1} \mathbf{Dfm}_n(M)\otimes^{\mathbb{L}}_{D(\Gamma_L,K),\mathrm{diag}}K \big)[-2] \\ & \cong \mathcal{T}_\Psi(D_n\tilde{\otimes}_{D}M ) \\ & \cong D_n{\otimes}_{D}\mathcal{T}_\Psi(M ) \end{align*} $$
$$ \begin{align*} K_{\Psi,D(\Gamma_L,K)}&(\mathbf{Dfm}_n(M))\\ & \cong \mathrm{cone} \big( \mathbf{Dfm}_n(M)\otimes^{\mathbb{L}}_{D(\Gamma_L,K),\mathrm{diag}}K\xrightarrow{\Psi-1} \mathbf{Dfm}_n(M)\otimes^{\mathbb{L}}_{D(\Gamma_L,K),\mathrm{diag}}K \big)[-2] \\ & \cong \mathcal{T}_\Psi(D_n\tilde{\otimes}_{D}M ) \\ & \cong D_n{\otimes}_{D}\mathcal{T}_\Psi(M ) \end{align*} $$
compatible for the variation in n by an obvious variant of Theorem 4.6 (2). Thus, combining [Reference Steingart51, Prop. 3.15] with Theorem 4.9 we obtain in
![]() $\mathbf {D}^b_{\mathrm {perf}}(D)$
an isomorphism
$\mathbf {D}^b_{\mathrm {perf}}(D)$
an isomorphism
This proves (ii) while (i) follows by the same arguments as in [Reference Steingart51, Rem. 3.16] using that the projective system
![]() $( K_{\Psi ,D(\Gamma _L,K)}(\mathbf {Dfm}_n(M)) )_m $
defines a consistent object in
$( K_{\Psi ,D(\Gamma _L,K)}(\mathbf {Dfm}_n(M)) )_m $
defines a consistent object in
![]() $\mathbf {D}(\mathrm {mod}(\mathbb {N},D))$
(using the notation of (loc. cit.)) together with the fact that D is a Fréchet-Stein algebra.
$\mathbf {D}(\mathrm {mod}(\mathbb {N},D))$
(using the notation of (loc. cit.)) together with the fact that D is a Fréchet-Stein algebra.
4.3 Replacing Local Tate duality
In this subsection we develop local duality analogous to local Tate duality for Galois cohomology, see [Reference Herr25, Reference Liu33] for an approach purely in terms of
![]() $(\varphi ,\Gamma )$
-modules. We focus technically on the complexes
$(\varphi ,\Gamma )$
-modules. We focus technically on the complexes
![]() $K_{f,{\mathfrak {Z}}}$
and shall then apply (12) to deal with
$K_{f,{\mathfrak {Z}}}$
and shall then apply (12) to deal with
![]() $K_{f,U}$
. Assume henceforth that M is an analytic
$K_{f,U}$
. Assume henceforth that M is an analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}=\mathcal {R}_K$
. For an analytic character
$\mathcal {R}=\mathcal {R}_K$
. For an analytic character
![]() $\delta : L^\times \to K^\times $
we define the twisted module
$\delta : L^\times \to K^\times $
we define the twisted module
![]() $M(\delta ) \in \mathfrak {M}^{an}(\mathcal {R}),$
where
$M(\delta ) \in \mathfrak {M}^{an}(\mathcal {R}),$
where
![]() $M(\delta ) := M\otimes _{\mathcal {R}}\mathcal {R}(\delta )$
endowed with the diagonal
$M(\delta ) := M\otimes _{\mathcal {R}}\mathcal {R}(\delta )$
endowed with the diagonal
![]() $\varphi _L$
- and
$\varphi _L$
- and
![]() $\Gamma _L$
-action. Recall the residue map (at Z)
$\Gamma _L$
-action. Recall the residue map (at Z)
and that the
![]() $(\varphi _L,\Gamma _L)$
-action on
$(\varphi _L,\Gamma _L)$
-action on
![]() $ \mathcal {R} dZ $
with respect to the basis
$ \mathcal {R} dZ $
with respect to the basis
![]() $d\log _{LT} = g_{LT}dZ$
is given by the character
$d\log _{LT} = g_{LT}dZ$
is given by the character
![]() $\chi _{LT}.$
Footnote
10
As a formal consequence, we have the following:
$\chi _{LT}.$
Footnote
10
As a formal consequence, we have the following:
Lemma 4.13. The map
 $$ \begin{align*} \mathcal{R}(\chi) & \xrightarrow{\;\cong\;} \Omega^1_{\mathcal{R}}, \\ f {\mathbf{e}_{\chi}} & \longmapsto fd\log_{LT} \otimes \mathbf{e}_{\delta^{un}_{\chi(\pi)}} , \end{align*} $$
$$ \begin{align*} \mathcal{R}(\chi) & \xrightarrow{\;\cong\;} \Omega^1_{\mathcal{R}}, \\ f {\mathbf{e}_{\chi}} & \longmapsto fd\log_{LT} \otimes \mathbf{e}_{\delta^{un}_{\chi(\pi)}} , \end{align*} $$
is an isomorphism of
![]() $(\varphi _L,\Gamma _L)$
-modules.
$(\varphi _L,\Gamma _L)$
-modules.
Setting
![]() $\tilde {M}:= \operatorname {Hom}_{\mathcal {R}}(M,{\mathcal {R}})(\chi ) \cong \operatorname {Hom}_{\mathcal {R}}(M,\Omega ^1_{\mathcal {R}}) $
, for any finitely generated projective
$\tilde {M}:= \operatorname {Hom}_{\mathcal {R}}(M,{\mathcal {R}})(\chi ) \cong \operatorname {Hom}_{\mathcal {R}}(M,\Omega ^1_{\mathcal {R}}) $
, for any finitely generated projective
![]() $\mathcal {R}$
-module M, we obtain more generally the pairing
$\mathcal {R}$
-module M, we obtain more generally the pairing
where by abuseFootnote
11
of notation we also write
![]() $Res:\mathcal {R}(\chi )\to K$
for the map sending
$Res:\mathcal {R}(\chi )\to K$
for the map sending
![]() $\sum _i a_iZ^i \otimes \mathbf {e}_{\chi }$
to
$\sum _i a_iZ^i \otimes \mathbf {e}_{\chi }$
to
![]() $a_{-1}.$
This map identifies M and
$a_{-1}.$
This map identifies M and
![]() $\tilde {M}$
with the (strong) topological duals of
$\tilde {M}$
with the (strong) topological duals of
![]() $\tilde {M}$
and M, respectively. Moreover, the isomorphism
$\tilde {M}$
and M, respectively. Moreover, the isomorphism
![]() $\tilde {M} \cong \operatorname {Hom}_{K,cts}(M,K)$
(induced by
$\tilde {M} \cong \operatorname {Hom}_{K,cts}(M,K)$
(induced by
![]() $ \langle \;,\;\rangle $
) is
$ \langle \;,\;\rangle $
) is
![]() $D(\Gamma _L,K)$
-linear by [Reference Schneider and Venjakob46, Corollary 4.5.4].
$D(\Gamma _L,K)$
-linear by [Reference Schneider and Venjakob46, Corollary 4.5.4].
Lemma 4.14. The residuum map induces an isomorphism
![]() $Res: H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}\cong K.$
$Res: H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}\cong K.$
Proof. We know from Lemma 4.22 that
![]() $\dim _K H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}=1$
while
$\dim _K H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}=1$
while
![]() $Res$
is a surjection
$Res$
is a surjection
![]() $\Omega ^1_{\mathcal {R}} \twoheadrightarrow K$
which factorizes over
$\Omega ^1_{\mathcal {R}} \twoheadrightarrow K$
which factorizes over
![]() $(\varphi _L-\operatorname {id})\Omega ^1_{\mathcal {R}}$
and
$(\varphi _L-\operatorname {id})\Omega ^1_{\mathcal {R}}$
and
![]() ${\mathfrak {Z}}\cdot \Omega ^1_{\mathcal {R}}$
by [Reference Schneider and Venjakob46, Lemma 4.5.1] or [Reference Colmez15, Prop. 1.5]. The claim follows as
${\mathfrak {Z}}\cdot \Omega ^1_{\mathcal {R}}$
by [Reference Schneider and Venjakob46, Lemma 4.5.1] or [Reference Colmez15, Prop. 1.5]. The claim follows as
![]() $H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}=H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )_{\Gamma _L}.$
$H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}=H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )_{\Gamma _L}.$
For compatibility questions we renormalise the residuum map to obtain the trace map
![]() $Tr=C_{Tr}({{\mathfrak {Z}}_n})Res:H_{\varphi _L,D(\Gamma _L)}^2(\Omega ^1_{\mathcal {R}} )=H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}\cong K$
by setting
$Tr=C_{Tr}({{\mathfrak {Z}}_n})Res:H_{\varphi _L,D(\Gamma _L)}^2(\Omega ^1_{\mathcal {R}} )=H_{\varphi _L,{\mathfrak {Z}}_n}^2(\Omega ^1_{\mathcal {R}} )^{\Gamma _L}\cong K$
by setting
 $$ \begin{align} C_{Tr}({{\mathfrak{Z}}_n}):=\frac{q}{q-1}\frac{\Omega}{\pi_L^n}. \end{align} $$
$$ \begin{align} C_{Tr}({{\mathfrak{Z}}_n}):=\frac{q}{q-1}\frac{\Omega}{\pi_L^n}. \end{align} $$
Note that for
![]() $L={\Bbb Q}_p$
and
$L={\Bbb Q}_p$
and
![]() $\pi _L=p$
this trace map is compatible with Tate’s trace map in Galois cohomology by [Reference Nakamura36, Prop. 5.2]. Independence of n follows by the same argument as for Definition 5.11 below. The principle is explained as follows:
$\pi _L=p$
this trace map is compatible with Tate’s trace map in Galois cohomology by [Reference Nakamura36, Prop. 5.2]. Independence of n follows by the same argument as for Definition 5.11 below. The principle is explained as follows:
The map of complexes, for
![]() $m\geq n$
,
$m\geq n$
,

induces the restriction maps
![]() $res^n_m:H^i_{{{\mathfrak {Z}}_n}}(M)\to H^i_{{{\mathfrak {Z}}_m}}(M),$
where
$res^n_m:H^i_{{{\mathfrak {Z}}_n}}(M)\to H^i_{{{\mathfrak {Z}}_m}}(M),$
where
![]() $\mathfrak {Q}_{m-n}({{\mathfrak {Z}}_n}):=\frac {{{\mathfrak {Z}}_m}}{{{\mathfrak {Z}}_n}}=\frac {\varphi _L^{m-n}({{\mathfrak {Z}}_n})}{{{\mathfrak {Z}}_n}}$
with
$\mathfrak {Q}_{m-n}({{\mathfrak {Z}}_n}):=\frac {{{\mathfrak {Z}}_m}}{{{\mathfrak {Z}}_n}}=\frac {\varphi _L^{m-n}({{\mathfrak {Z}}_n})}{{{\mathfrak {Z}}_n}}$
with
![]() $\mathfrak {Q}_{m-n}(0)=\pi _L^{m-n}.$
Since
$\mathfrak {Q}_{m-n}(0)=\pi _L^{m-n}.$
Since
![]() $C_{Tr}({{\mathfrak {Z}}_n})= \pi _L^{m-n}C_{Tr}({{\mathfrak {Z}}_m})$
by (48) the isomorphism
$C_{Tr}({{\mathfrak {Z}}_n})= \pi _L^{m-n}C_{Tr}({{\mathfrak {Z}}_m})$
by (48) the isomorphism
into the
![]() $\Gamma _L$
-coinvariants is compatible with
$\Gamma _L$
-coinvariants is compatible with
![]() $res^n_m,$
i.e., the diagram
$res^n_m,$
i.e., the diagram

commutes.
For a complex
![]() $(X^\bullet , d_X )$
of topological K-vector spaces we define its K-dual
$(X^\bullet , d_X )$
of topological K-vector spaces we define its K-dual
![]() $((X^*)^\bullet , d_{X^*})$
to be the complex with
$((X^*)^\bullet , d_{X^*})$
to be the complex with
and
The following lemma is taken from [Reference Schneider and Venjakob46, Lemma 5.2.4 and Remark 5.2.6].
Lemma 4.15. Let
![]() $(\mathcal {C}^\bullet ,d^\bullet )$
be a complex in the category of locally convex topological F-vector spaces.
$(\mathcal {C}^\bullet ,d^\bullet )$
be a complex in the category of locally convex topological F-vector spaces.
-
(i) If
 $\mathcal {C}$
consists of Fréchet spaces and
$\mathcal {C}$
consists of Fréchet spaces and
 $h^i(\mathcal {C}^\bullet )$
is finite-dimensional over F, then
$h^i(\mathcal {C}^\bullet )$
is finite-dimensional over F, then
 $d^{i-1}$
is strict and has closed image.
$d^{i-1}$
is strict and has closed image. -
(ii) If
 $d^{i}$
is strict and either F is spherically complete or the spaces involved in degree i are of countable typeFootnote
12
, then
$d^{i}$
is strict and either F is spherically complete or the spaces involved in degree i are of countable typeFootnote
12
, then
 $h^{-i}(\mathcal {C}^*)\cong h^{i}(\mathcal {C})^*.$
$h^{-i}(\mathcal {C}^*)\cong h^{i}(\mathcal {C})^*.$
-
(iii) If
 $\mathcal {C}^\bullet $
consists of
$\mathcal {C}^\bullet $
consists of
 $LF$
-spaces,
$LF$
-spaces,
 $\mathcal {C}^{i+2}=0$
and
$\mathcal {C}^{i+2}=0$
and
 $h^i(\mathcal {C}^\bullet )$
is finite dimensional, then
$h^i(\mathcal {C}^\bullet )$
is finite dimensional, then
 $d^i$
is strict.
$d^i$
is strict. -
(iv) If
 $V\xrightarrow {\alpha } W$
is a continuous linear map of Hausdorff
$V\xrightarrow {\alpha } W$
is a continuous linear map of Hausdorff
 $LF$
-spaces over F with finite dimensional cokernel, then
$LF$
-spaces over F with finite dimensional cokernel, then
 $\alpha $
is strict and has closed image.
$\alpha $
is strict and has closed image.
The translation
![]() $X[n]$
of a complex X is given by
$X[n]$
of a complex X is given by
![]() $X[n]^i:=X^{i+n}$
and
$X[n]^i:=X^{i+n}$
and
![]() $d^i_{X[n]}:=(-1)^nd_X^{i+n}.$
$d^i_{X[n]}:=(-1)^nd_X^{i+n}.$
Let
![]() $\iota $
denote the involution on
$\iota $
denote the involution on
![]() $D(o_L,K)$
induced by the inversion on the group
$D(o_L,K)$
induced by the inversion on the group
![]() $o_L$
. We observe that
$o_L$
. We observe that
for a unit
![]() $\lambda \in D(o_L,K)$
as they both generate the augmentation ideal: more explicitly,
$\lambda \in D(o_L,K)$
as they both generate the augmentation ideal: more explicitly,
![]() ${\mathfrak {Z}}^\iota =[-1]({{\mathfrak {Z}}}), \lambda ^{-1}=\lambda ^\iota $
.
${\mathfrak {Z}}^\iota =[-1]({{\mathfrak {Z}}}), \lambda ^{-1}=\lambda ^\iota $
.
Theorem 4.16.
-
(i) There is a canonical quasi-isomorphism
(23)
-
(ii) Via the pairing (19) there are canonical isomorphisms of complexes in the derived category
 $\mathbf {D}(K)$
given by the following diagram of quasi-isomorphisms
$\mathbf {D}(K)$
given by the following diagram of quasi-isomorphisms $$\begin{align*}K_{\varphi_L,{\mathfrak{Z}}}(M)^*\cong K_{\Psi_L,{{\mathfrak{Z}}}^\iota}({M})^*{ \cong} K_{\varphi_L,{\mathfrak{Z}}}({M}^*)[2]{ \cong} K_{\varphi_L,{\mathfrak{Z}}}(\tilde{M})[2].\end{align*}$$
(24)
$$\begin{align*}K_{\varphi_L,{\mathfrak{Z}}}(M)^*\cong K_{\Psi_L,{{\mathfrak{Z}}}^\iota}({M})^*{ \cong} K_{\varphi_L,{\mathfrak{Z}}}({M}^*)[2]{ \cong} K_{\varphi_L,{\mathfrak{Z}}}(\tilde{M})[2].\end{align*}$$
(24)
with
 $\Upsilon =(-\Psi \oplus \lambda )^*: (M\bigoplus M)^*\to (M\bigoplus M)^*$
and
$\Upsilon =(-\Psi \oplus \lambda )^*: (M\bigoplus M)^*\to (M\bigoplus M)^*$
and
 $\Xi (x,y)= y\oplus - x$
. In particular, we obtain isomorphisms (25)induced by the perfect pairings, denoted by
$\Xi (x,y)= y\oplus - x$
. In particular, we obtain isomorphisms (25)induced by the perfect pairings, denoted by $$ \begin{align} H^i_{\varphi_L,{\mathfrak{Z}}}(M)^* &\cong H^{2-i}_{\Psi_L,{\mathfrak{Z}}}(\tilde{M}){\cong} H^{2-i}_{\varphi_L,{\mathfrak{Z}}}(\tilde{M}). \end{align} $$
$$ \begin{align} H^i_{\varphi_L,{\mathfrak{Z}}}(M)^* &\cong H^{2-i}_{\Psi_L,{\mathfrak{Z}}}(\tilde{M}){\cong} H^{2-i}_{\varphi_L,{\mathfrak{Z}}}(\tilde{M}). \end{align} $$
 $\langle -,-\rangle :=\langle -,-\rangle _M$
,
$\langle -,-\rangle :=\langle -,-\rangle _M$
,  $$\begin{align*}H^1_{\varphi, {\mathfrak{Z}}}(M) \times H^1_{\varphi, {\mathfrak{Z}}}(\tilde{M}) \to K, (\overline{(m,n)},\overline{(f,g)})\mapsto -Res\Big(\varphi(g)(m)+({\lambda}^\iota f)( n)\Big),\end{align*}$$
$$\begin{align*}H^1_{\varphi, {\mathfrak{Z}}}(M) \times H^1_{\varphi, {\mathfrak{Z}}}(\tilde{M}) \to K, (\overline{(m,n)},\overline{(f,g)})\mapsto -Res\Big(\varphi(g)(m)+({\lambda}^\iota f)( n)\Big),\end{align*}$$
 $$\begin{align*}H^2_{\varphi, {\mathfrak{Z}}}(M) \times H^0_{\varphi, {\mathfrak{Z}}}(\tilde{M}) \to K, (\overline{m},\tilde{n})\mapsto -Res \Big(\tilde{n}(\lambda^\iota\varphi(m))\Big) ,\end{align*}$$
$$\begin{align*}H^2_{\varphi, {\mathfrak{Z}}}(M) \times H^0_{\varphi, {\mathfrak{Z}}}(\tilde{M}) \to K, (\overline{m},\tilde{n})\mapsto -Res \Big(\tilde{n}(\lambda^\iota\varphi(m))\Big) ,\end{align*}$$
 $$\begin{align*}H^0_{\varphi, {\mathfrak{Z}}}(M) \times H^2_{\varphi, {\mathfrak{Z}}}(\tilde{M}) \to K, ({m},\overline{\tilde{n}})\mapsto Res \Big(\tilde{n}(m)\Big).\end{align*}$$
$$\begin{align*}H^0_{\varphi, {\mathfrak{Z}}}(M) \times H^2_{\varphi, {\mathfrak{Z}}}(\tilde{M}) \to K, ({m},\overline{\tilde{n}})\mapsto Res \Big(\tilde{n}(m)\Big).\end{align*}$$
Remark 4.17. Identify M with
![]() $\tilde {\tilde {M}}$
via
$\tilde {\tilde {M}}$
via
![]() $m \mapsto m^{**}$
and consider the pairing in degree
$m \mapsto m^{**}$
and consider the pairing in degree
![]() $(1,1)$
from Theorem 4.16 obtained by exchanging the roles of M and
$(1,1)$
from Theorem 4.16 obtained by exchanging the roles of M and
![]() $\tilde {M},$
i.e.,
$\tilde {M},$
i.e.,
 $$ \begin{align*} \langle -,- \rangle_{\tilde{M}} \colon H^1_{\varphi,\mathfrak{Z}}(\tilde{M}) \times H^1_{\varphi,\mathfrak{Z}}(\tilde{\tilde{M}})&\to K,\\ ((f,g),(m^{**},n^{**})) &\mapsto -\operatorname{Res}(\varphi(n^{**})(f)+(\lambda^{\iota}m^{**})(g)). \end{align*} $$
$$ \begin{align*} \langle -,- \rangle_{\tilde{M}} \colon H^1_{\varphi,\mathfrak{Z}}(\tilde{M}) \times H^1_{\varphi,\mathfrak{Z}}(\tilde{\tilde{M}})&\to K,\\ ((f,g),(m^{**},n^{**})) &\mapsto -\operatorname{Res}(\varphi(n^{**})(f)+(\lambda^{\iota}m^{**})(g)). \end{align*} $$
We have
In the other degrees consider
 $$ \begin{align*} \langle -,- \rangle_{\tilde{M}}\colon H^2_{\varphi,\mathfrak{Z}}(\tilde{M}) \times H^0_{\varphi,\mathfrak{Z}}(\tilde{\tilde{M}})&\to K,\\ { (\overline{f}, m^{**})} &\mapsto \operatorname{Res}(m^{**}(-\lambda^\iota(\varphi(f)))), \end{align*} $$
$$ \begin{align*} \langle -,- \rangle_{\tilde{M}}\colon H^2_{\varphi,\mathfrak{Z}}(\tilde{M}) \times H^0_{\varphi,\mathfrak{Z}}(\tilde{\tilde{M}})&\to K,\\ { (\overline{f}, m^{**})} &\mapsto \operatorname{Res}(m^{**}(-\lambda^\iota(\varphi(f)))), \end{align*} $$
satisfying
![]() $\langle \overline {f}, {m^{**}}\rangle _{\tilde {M}} = \langle {m},\overline {f} \rangle _{M}$
and
$\langle \overline {f}, {m^{**}}\rangle _{\tilde {M}} = \langle {m},\overline {f} \rangle _{M}$
and
 $$ \begin{align*} H^0_{\varphi,\mathfrak{Z}}(\tilde{M}) \times H^2_{\varphi,\mathfrak{Z}}(\tilde{\tilde{M}})&\to K,\\ (g,\overline{n^{**}}) &\mapsto \operatorname{Res}({ n^{**}(g)}), \end{align*} $$
$$ \begin{align*} H^0_{\varphi,\mathfrak{Z}}(\tilde{M}) \times H^2_{\varphi,\mathfrak{Z}}(\tilde{\tilde{M}})&\to K,\\ (g,\overline{n^{**}}) &\mapsto \operatorname{Res}({ n^{**}(g)}), \end{align*} $$
satisfying
![]() $\langle g,\overline {n^{**}}\rangle _{\tilde {M}} = \langle \overline {n},g \rangle _{M}.$
Footnote
13
$\langle g,\overline {n^{**}}\rangle _{\tilde {M}} = \langle \overline {n},g \rangle _{M}.$
Footnote
13
Proof. By viewing
![]() $K_{\varphi ,\mathfrak {Z}}(\tilde {M})$
as a Koszul complex attached to the automorphisms
$K_{\varphi ,\mathfrak {Z}}(\tilde {M})$
as a Koszul complex attached to the automorphisms
![]() $\varphi -1,\mathfrak {Z}$
of M one can see that
$\varphi -1,\mathfrak {Z}$
of M one can see that
![]() $\mathfrak {Z}$
and
$\mathfrak {Z}$
and
![]() $\varphi _L-1$
act as
$\varphi _L-1$
act as
![]() $0$
on the cohomology groups. Since
$0$
on the cohomology groups. Since
we see that the class
![]() $\overline {(f,g)} \in H^1_{\varphi ,\mathfrak {Z}}(\tilde {M})$
is equal to the class of
$\overline {(f,g)} \in H^1_{\varphi ,\mathfrak {Z}}(\tilde {M})$
is equal to the class of
![]() $\overline {(-\lambda f,- \lambda g)}.$
Now let
$\overline {(-\lambda f,- \lambda g)}.$
Now let
![]() $ \overline {(m,n)} \in H^1_{\varphi ,\mathfrak {Z}}(M).$
Using
$ \overline {(m,n)} \in H^1_{\varphi ,\mathfrak {Z}}(M).$
Using
![]() $\mathfrak {Z}f = (\varphi -1)g$
and
$\mathfrak {Z}f = (\varphi -1)g$
and
![]() $\mathfrak {Z}m = (\varphi -1)n$
we compute
$\mathfrak {Z}m = (\varphi -1)n$
we compute
 $$ \begin{align*} \langle \overline{(m,n)},\overline{(f,g)}\rangle_{M} &= Res\Big(-\varphi(g)(m)-(\lambda^\iota f)(n)\Big)\\ &= Res\Big(-[g+\mathfrak{Z}f](m)-(\lambda^\iota f)(\varphi(n)-\mathfrak{Z}m)\Big)\\ &= Res\Big(-g(m)-(\lambda^\iota f)\varphi(n))- \underbrace{(\mathfrak{Z}f)(m) + (\lambda^\iota \mathfrak{Z}^\iota f)(m)}_{=0}\Big)\\ & = Res\Big((\lambda g)(m)+(\lambda \lambda^\iota f)(\varphi(n))\Big)\\ & = Res\Big(m^{**}(\lambda g)+\varphi(n^{**})( f)\Big)\\ & = - \langle \overline{(f,g)},\overline{(m^{**},n^{**})} \rangle_{\tilde{M}}, \end{align*} $$
$$ \begin{align*} \langle \overline{(m,n)},\overline{(f,g)}\rangle_{M} &= Res\Big(-\varphi(g)(m)-(\lambda^\iota f)(n)\Big)\\ &= Res\Big(-[g+\mathfrak{Z}f](m)-(\lambda^\iota f)(\varphi(n)-\mathfrak{Z}m)\Big)\\ &= Res\Big(-g(m)-(\lambda^\iota f)\varphi(n))- \underbrace{(\mathfrak{Z}f)(m) + (\lambda^\iota \mathfrak{Z}^\iota f)(m)}_{=0}\Big)\\ & = Res\Big((\lambda g)(m)+(\lambda \lambda^\iota f)(\varphi(n))\Big)\\ & = Res\Big(m^{**}(\lambda g)+\varphi(n^{**})( f)\Big)\\ & = - \langle \overline{(f,g)},\overline{(m^{**},n^{**})} \rangle_{\tilde{M}}, \end{align*} $$
where in the fifth equation we replace
![]() $\overline {(f,g)}$
with
$\overline {(f,g)}$
with
![]() $(-\lambda f,-\lambda g).$
Now consider the degree
$(-\lambda f,-\lambda g).$
Now consider the degree
![]() $(0,2)$
case with regard to
$(0,2)$
case with regard to
![]() $\langle -,-\rangle _M$
. Since
$\langle -,-\rangle _M$
. Since
![]() $\overline {\varphi (f)} = \overline {f}$
we get
$\overline {\varphi (f)} = \overline {f}$
we get
![]() $\operatorname {Res}(f(m)) = \operatorname {Res}(\varphi (f)(m)) = - \operatorname {Res}(\varphi (f)(\lambda m))$
using that
$\operatorname {Res}(f(m)) = \operatorname {Res}(\varphi (f)(m)) = - \operatorname {Res}(\varphi (f)(\lambda m))$
using that
![]() $\mathfrak {Z}{m} = 0$
in
$\mathfrak {Z}{m} = 0$
in
![]() $H^0$
and hence
$H^0$
and hence
![]() $\lambda {m} =-{m}.$
The computation in degree
$\lambda {m} =-{m}.$
The computation in degree
![]() $(2,0)$
is similar.
$(2,0)$
is similar.
Later in explicit calculations we will need to work partly with
![]() $\Psi $
-versions, which we therefore establish in the next remark.
$\Psi $
-versions, which we therefore establish in the next remark.
Remark 4.18. As a obvious variant of (i) in Theorem 4.16 there is also a canonical quasi-isomorphism

In particular, we obtain an isomorphism
![]() $\Upsilon ^{\prime }_M: H^1_{\varphi _L,{\mathfrak {Z}}}(M)\cong H^1_{\Psi _L,{\mathfrak {Z}}}(M)$
sending a class
$\Upsilon ^{\prime }_M: H^1_{\varphi _L,{\mathfrak {Z}}}(M)\cong H^1_{\Psi _L,{\mathfrak {Z}}}(M)$
sending a class
![]() $[(x,y)]$
to the class
$[(x,y)]$
to the class
![]() $[(-\Psi (x),y)].$
$[(-\Psi (x),y)].$
Using this one derives from
![]() $\langle -, - \rangle _M$
in Theorem 4.16 the (asymmetric) perfect pairings, denoted by
$\langle -, - \rangle _M$
in Theorem 4.16 the (asymmetric) perfect pairings, denoted by
![]() $\{\!\!\{ -, - \}\!\!\}_M,$
$\{\!\!\{ -, - \}\!\!\}_M,$
for which by construction we have
Moreover, we obtain, for
![]() $x\in H^i_{\varphi , {{\mathfrak {Z}}} }({M}),\ y\in H^{2-i}_{\varphi , {{\mathfrak {Z}}} }(\tilde {M}),$
$x\in H^i_{\varphi , {{\mathfrak {Z}}} }({M}),\ y\in H^{2-i}_{\varphi , {{\mathfrak {Z}}} }(\tilde {M}),$
by Remark 4.17.
Proof of the Theorem
(i) is an immediate consequence Lemma 4.4. Now consider (ii): The first isomorphism is induced by (i). Up to signs,
![]() $(-)^*$
transforms
$(-)^*$
transforms
![]() $\varphi _L$
into
$\varphi _L$
into
![]() $\psi _L$
and
$\psi _L$
and
![]() ${\mathfrak {Z}}$
into
${\mathfrak {Z}}$
into
![]() ${\mathfrak {Z}}^\iota $
. Using that
${\mathfrak {Z}}^\iota $
. Using that
![]() ${\mathfrak {Z}}^\iota =\lambda {\mathfrak {Z}}$
one easily verifies that also the second map is an isomorphism. Finally, the last isomorphism stems from the identification
${\mathfrak {Z}}^\iota =\lambda {\mathfrak {Z}}$
one easily verifies that also the second map is an isomorphism. Finally, the last isomorphism stems from the identification
![]() $M^*\cong \tilde {M}$
by [Reference Schneider and Venjakob46, Cor. 4.5.4].
$M^*\cong \tilde {M}$
by [Reference Schneider and Venjakob46, Cor. 4.5.4].
For the pairing on the level of cohomology groups, we want to apply (ii) of Lemma 4.15, for which we have to check strictness of the differentials. But this is not sufficient: in order to get perfectness of the pairings - which amounts to an algebraic duality while the functor
![]() $(-)^*$
only measures continuous duals - we also have to check that the induced topology on the cohomology groups is Hausdorff. In detail this boils down to the following reasoning: Since by 4.6 all the
$(-)^*$
only measures continuous duals - we also have to check that the induced topology on the cohomology groups is Hausdorff. In detail this boils down to the following reasoning: Since by 4.6 all the
![]() $H^i_{\varphi _L,{\mathfrak {Z}}}(M)$
are finite-dimensional, we may apply Lemma 4.15(iii) to first conclude that
$H^i_{\varphi _L,{\mathfrak {Z}}}(M)$
are finite-dimensional, we may apply Lemma 4.15(iii) to first conclude that
![]() $d^1$
(and trivially
$d^1$
(and trivially
![]() $d^2$
) is strict. By the same reasoning for
$d^2$
) is strict. By the same reasoning for
![]() $H^i_{\varphi ,\mathfrak {Z}}(\tilde {M})$
the
$H^i_{\varphi ,\mathfrak {Z}}(\tilde {M})$
the
![]() $d^1$
-differential of
$d^1$
-differential of
![]() $K_{\Psi ,{\mathfrak {Z}^\iota }}(M^*)$
is strict. Moreover, the
$K_{\Psi ,{\mathfrak {Z}^\iota }}(M^*)$
is strict. Moreover, the
![]() $H^2$
s are always Hausdorff by 4.15 (iv) and we note that the
$H^2$
s are always Hausdorff by 4.15 (iv) and we note that the
![]() $H^0$
are always Hausdorff (as they are subspaces of Hausdorff spaces). Applying 4.15 (ii) and using that for a finite dimensional Hausdorff space the continuous and algebraic dual agree we conclude the claim for the pairings involving
$H^0$
are always Hausdorff (as they are subspaces of Hausdorff spaces). Applying 4.15 (ii) and using that for a finite dimensional Hausdorff space the continuous and algebraic dual agree we conclude the claim for the pairings involving
![]() $H^0$
and
$H^0$
and
![]() $H^2$
. By the strictness of
$H^2$
. By the strictness of
![]() $d_1$
we have
$d_1$
we have
![]() $H^1_{\varphi ,\mathfrak {Z}}(M)^* \cong H^1_{\varphi ,\mathfrak {Z}}(\tilde {M})$
and, vice versa,
$H^1_{\varphi ,\mathfrak {Z}}(M)^* \cong H^1_{\varphi ,\mathfrak {Z}}(\tilde {M})$
and, vice versa,
![]() $H^1_{\varphi ,\mathfrak {Z}}(\tilde {M})^* \cong H^1_{\varphi ,\mathfrak {Z}}(M).$
A priori we don’t know if the finite dimensional
$H^1_{\varphi ,\mathfrak {Z}}(\tilde {M})^* \cong H^1_{\varphi ,\mathfrak {Z}}(M).$
A priori we don’t know if the finite dimensional
![]() $H^1$
s are Hausdorff but combining both isomorphisms we see that
$H^1$
s are Hausdorff but combining both isomorphisms we see that
![]() $(H^1_{\varphi ,\mathfrak {Z}}(M)^*)^*$
has the same dimension as
$(H^1_{\varphi ,\mathfrak {Z}}(M)^*)^*$
has the same dimension as
![]() $H^1_{\varphi ,\mathfrak {Z}}(M)$
which for a finite dimensional space can only occur, if every functional is continuous, forcing the
$H^1_{\varphi ,\mathfrak {Z}}(M)$
which for a finite dimensional space can only occur, if every functional is continuous, forcing the
![]() $H^1$
s to be Hausdorff, which allows us to argue analogously for the pairing of
$H^1$
s to be Hausdorff, which allows us to argue analogously for the pairing of
![]() $H^1$
s.
$H^1$
s.
4.4 Cohomological computations in the character case
Recall [Reference Schneider and Teitelbaum42, Lem. 4.6] or [Reference Colmez15, §2] for the following. The Amice-Katz transform is the map
sending a distribution
![]() $\mu $
to
$\mu $
to
satisfying:
-
(i)
 $A_-$
is a
$A_-$
is a
 $\varphi $
- and
$\varphi $
- and
 $\Gamma _L$
-equivariant topological isomorphism of rings.
$\Gamma _L$
-equivariant topological isomorphism of rings. -
(ii) for
 $z\in o_K$
with
$z\in o_K$
with
 $v_p(z)>0$
:
$v_p(z)>0$
:
 $A_{\eta (x,z)\mu }(Z)=A_\mu (Z+_{LT}z),$
where
$A_{\eta (x,z)\mu }(Z)=A_\mu (Z+_{LT}z),$
where
 $\int _{o_L}g(x)(f\cdot \mu )(x)=\int _{o_L}f(x)g(x)\mu (x)$
for any locally analytic function
$\int _{o_L}g(x)(f\cdot \mu )(x)=\int _{o_L}f(x)g(x)\mu (x)$
for any locally analytic function
 $f:o_L\to \mathbb {C}_p.$
$f:o_L\to \mathbb {C}_p.$
-
(iii) (multiplicativity regarding convolution)
 $A_{\lambda *\mu }=A_\lambda \cdot A_\mu $
$A_{\lambda *\mu }=A_\lambda \cdot A_\mu $
-
(iv)
 $A_{\mathrm {Res}_{b+\pi _L^no_L}(\mu )}=\frac {1 }{q^n}\sum _{[\pi _L^n](a)=0}\eta (-b,a)A_\mu (Z+_{LT}a)=\mathrm {Res}_{b+\pi _L^no_L}A_\mu ,$
where the latter denotes the multiplication with the corresponding characteristic function.
$A_{\mathrm {Res}_{b+\pi _L^no_L}(\mu )}=\frac {1 }{q^n}\sum _{[\pi _L^n](a)=0}\eta (-b,a)A_\mu (Z+_{LT}a)=\mathrm {Res}_{b+\pi _L^no_L}A_\mu ,$
where the latter denotes the multiplication with the corresponding characteristic function. -
(v)
 $\partial A_\mu =A_{{\Omega }x\mu }$
where
$\partial A_\mu =A_{{\Omega }x\mu }$
where
 $\partial =\frac {d}{dt_{LT}}=\frac {1}{\log _{LT}'}\frac {d}{dZ}=\Omega \eta (1,Z)\frac {d}{d\eta (1,Z)}.$
Footnote
14
$\partial =\frac {d}{dt_{LT}}=\frac {1}{\log _{LT}'}\frac {d}{dZ}=\Omega \eta (1,Z)\frac {d}{d\eta (1,Z)}.$
Footnote
14
-
(vi)
 $A_{d\mu }=t_{LT}A_\mu ,$
where
$A_{d\mu }=t_{LT}A_\mu ,$
where
 $\int _{o_L}f(x)(d\mu )(x)=\int _{o_L}f'(x)\mu (x)$
with
$\int _{o_L}f(x)(d\mu )(x)=\int _{o_L}f'(x)\mu (x)$
with
 $f'(x)=\frac {d}{dx}f.$
$f'(x)=\frac {d}{dx}f.$
Lemma 4.19. (Mellin transform) The natural inclusion
![]() $D(o_L^\times ,K)\hookrightarrow D(o_L,K)$
combined with the Fourier isomorphism induces the map
$D(o_L^\times ,K)\hookrightarrow D(o_L,K)$
combined with the Fourier isomorphism induces the map

which is a topological isomorphism of
![]() $D(o_L^\times ,K)$
-modules. Here
$D(o_L^\times ,K)$
-modules. Here
![]() $\operatorname {ev}_1$
denotes the map on the character variety which evaluates a character in
$\operatorname {ev}_1$
denotes the map on the character variety which evaluates a character in
![]() $1$
. Moreover, we have a commutative diagram
$1$
. Moreover, we have a commutative diagram

where
![]() $\mathfrak {M}$
denotes the Mellin transform, which by definition sends
$\mathfrak {M}$
denotes the Mellin transform, which by definition sends
![]() $\mu $
to
$\mu $
to
 $$\begin{align*}\mu\cdot \eta(1,Z)=\int_{o_L^\times} \eta(x,Z)\mu(x),\end{align*}$$
$$\begin{align*}\mu\cdot \eta(1,Z)=\int_{o_L^\times} \eta(x,Z)\mu(x),\end{align*}$$
see [Reference Schneider and Venjakob46, §2.1.4, Lem. 2.6, Thm. 2.33,§2.2.7].
Proof.
![]() $\mu \in D(o_L^\times )\subseteq D(o_L)$
satisfies
$\mu \in D(o_L^\times )\subseteq D(o_L)$
satisfies
![]() $\mathrm {Res}_{o_L^\times }(\mu )=\mu ,$
whence
$\mathrm {Res}_{o_L^\times }(\mu )=\mu ,$
whence
![]() $A_\mu (Z)=\int _{o_L}\eta (x,Z)\mu (x)=\int _{o_L^\times }\eta (x,Z)\mu (x)=\mathfrak {M}(\mu ).$
$A_\mu (Z)=\int _{o_L}\eta (x,Z)\mu (x)=\int _{o_L^\times }\eta (x,Z)\mu (x)=\mathfrak {M}(\mu ).$
We write
![]() $LA(o_L):=LA(o_L,K)$
for the set of locally L-analytic functions
$LA(o_L):=LA(o_L,K)$
for the set of locally L-analytic functions
![]() $\phi :o_L\to K$
endowed with the following operators:
$\phi :o_L\to K$
endowed with the following operators:
 $$ \begin{align*} \varphi(\phi)(x):=&\left\{ \begin{array}{ll} \phi(\frac{x}{\pi_L}), & \text{if } x \in \pi_Lo_L; \\ 0, & \text{otherwise.} \end{array} \right. \\ \Psi(\phi)(x):= & \phi(\pi_Lx) \\ \gamma(\phi)(x):= & \phi(\chi_{LT}^{-1}(\gamma)x). \end{align*} $$
$$ \begin{align*} \varphi(\phi)(x):=&\left\{ \begin{array}{ll} \phi(\frac{x}{\pi_L}), & \text{if } x \in \pi_Lo_L; \\ 0, & \text{otherwise.} \end{array} \right. \\ \Psi(\phi)(x):= & \phi(\pi_Lx) \\ \gamma(\phi)(x):= & \phi(\chi_{LT}^{-1}(\gamma)x). \end{align*} $$
By [Reference Colmez13, Thm. 2.3] (for the exact sequence), [Reference Berger and Fourquaux6, Cor. 2.3.4] (for the surjectivity on
![]() $\mathcal {R}_K^+(\delta )$
), we have for all
$\mathcal {R}_K^+(\delta )$
), we have for all
![]() $\delta \in \Sigma _{an} $
the following commutative diagram of
$\delta \in \Sigma _{an} $
the following commutative diagram of
![]() $D(\Gamma _L,L)$
-modules with exact rows
$D(\Gamma _L,L)$
-modules with exact rows

which we can also interpret as short exact sequence of complexes of
![]() $D(\Gamma _L,L)$
-modules
$D(\Gamma _L,L)$
-modules
with
![]() $\mathcal {T}_\Psi (\mathcal {R}_K^+(\delta ))\cong (\mathcal {R}_K^+(\delta ))^{\Psi =1}[0]$
in degree zero. Here the map
$\mathcal {T}_\Psi (\mathcal {R}_K^+(\delta ))\cong (\mathcal {R}_K^+(\delta ))^{\Psi =1}[0]$
in degree zero. Here the map
![]() $\mathcal {R}_K(\delta )\to LA(o_L)(\chi ^{-1}\delta )$
sends
$\mathcal {R}_K(\delta )\to LA(o_L)(\chi ^{-1}\delta )$
sends
![]() $f\mathbf {e}_\delta $
to
$f\mathbf {e}_\delta $
to
![]() $\phi _f \mathbf {e}_{\chi ^{-1}\delta }$
withFootnote
15
$\phi _f \mathbf {e}_{\chi ^{-1}\delta }$
withFootnote
15
In particular we obtain a short exact sequence
and an isomorphism
Let
![]() $Pol_{\leq N}(o_L):=Pol_{\leq N}(o_L,K):=\bigoplus _{i=0}^NKz^i\subseteq LA(o_L)$
denote the polynomial functions on
$Pol_{\leq N}(o_L):=Pol_{\leq N}(o_L,K):=\bigoplus _{i=0}^NKz^i\subseteq LA(o_L)$
denote the polynomial functions on
![]() $o_L$
. This subspace is
$o_L$
. This subspace is
![]() $\Gamma _L$
- and
$\Gamma _L$
- and
![]() $\Psi $
-stable, more precisely we have
$\Psi $
-stable, more precisely we have
 $$ \begin{align*} \Psi(z^i)&= \pi_L^i z^i \\ \gamma(z^i) &= \chi_{LT}^{-i}z^i. \end{align*} $$
$$ \begin{align*} \Psi(z^i)&= \pi_L^i z^i \\ \gamma(z^i) &= \chi_{LT}^{-i}z^i. \end{align*} $$
for all
![]() $i\geq 0$
and
$i\geq 0$
and
![]() $\gamma \in \Gamma _L.$
In particular, we obtain, for
$\gamma \in \Gamma _L.$
In particular, we obtain, for
![]() $i=0,1$
,
$i=0,1$
,
 $$ \begin{align} H^i_\Psi(Pol_{\leq N}(o_L)(\chi^{-1}\delta))\cong \left\{ \begin{array}{@{}ll} K z^k\mathbf{e}_{\delta\chi^{-1}}, & \text{if } \delta(\pi_L)=\frac{\pi_L^{k+1}}{q} \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise.} \end{array} \right. \end{align} $$
$$ \begin{align} H^i_\Psi(Pol_{\leq N}(o_L)(\chi^{-1}\delta))\cong \left\{ \begin{array}{@{}ll} K z^k\mathbf{e}_{\delta\chi^{-1}}, & \text{if } \delta(\pi_L)=\frac{\pi_L^{k+1}}{q} \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise.} \end{array} \right. \end{align} $$
It follows that
 $$ \begin{align} H^j_{{\mathfrak{Z}}}( H^i_\Psi(Pol_{\leq N}(o_L)(\chi^{-1}\delta)))\cong \left\{ \begin{array}{@{}ll} K z^k\mathbf{e}_{\delta\chi^{-1}}, & \text{if } \delta =x^k\chi \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise.} \end{array} \right. \end{align} $$
$$ \begin{align} H^j_{{\mathfrak{Z}}}( H^i_\Psi(Pol_{\leq N}(o_L)(\chi^{-1}\delta)))\cong \left\{ \begin{array}{@{}ll} K z^k\mathbf{e}_{\delta\chi^{-1}}, & \text{if } \delta =x^k\chi \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise.} \end{array} \right. \end{align} $$
Lemma 4.20. For
![]() $N>v_\pi (\chi ^{-1}\delta (\pi ))$
we have a quasi-isomorphism
$N>v_\pi (\chi ^{-1}\delta (\pi ))$
we have a quasi-isomorphism
and an isomorphism
as L-vector spaces.
Proof. (see [Reference Chenevier11, Lem. 2.9] for the cyclotomic case, even over affinoid algebras A instead of L). Use the decomposition
![]() $LA(o_L)\cong x^{N+1}LA(o_L) \oplus Pol_{\leq N}(o_L)$
and show that for N as in the assumption
$LA(o_L)\cong x^{N+1}LA(o_L) \oplus Pol_{\leq N}(o_L)$
and show that for N as in the assumption
![]() $\Psi -1$
is a topological isomorphism on
$\Psi -1$
is a topological isomorphism on
![]() $x^{N+1}LA(o_L).$
$x^{N+1}LA(o_L).$
Similarly, regarding the
![]() $\Gamma _L$
- and
$\Gamma _L$
- and
![]() $\Psi $
-stable submodule
$\Psi $
-stable submodule
![]() $D_{N}:=D_{K,N}:=\bigoplus _{l=0}^NKt_{LT}^l\subseteq \mathcal {R}_K^+$
we obtain for
$D_{N}:=D_{K,N}:=\bigoplus _{l=0}^NKt_{LT}^l\subseteq \mathcal {R}_K^+$
we obtain for
![]() $i,j\in \{0,1\}$
,
$i,j\in \{0,1\}$
,
 $$ \begin{align} H^i_\Psi(D_{N}(\delta))\cong \left\{ \begin{array}{@{}ll} K t_{LT}^k\mathbf{e}_{\delta}, & \text{if } \delta(\pi_L)= \pi_L^{-k} \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise,} \end{array} \right. \end{align} $$
$$ \begin{align} H^i_\Psi(D_{N}(\delta))\cong \left\{ \begin{array}{@{}ll} K t_{LT}^k\mathbf{e}_{\delta}, & \text{if } \delta(\pi_L)= \pi_L^{-k} \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise,} \end{array} \right. \end{align} $$
and
 $$ \begin{align} H^j_{{\mathfrak{Z}}}( H^i_\Psi(D_{N}(\delta)))\cong \left\{ \begin{array}{ll} K t_{LT}^k\mathbf{e}_{\delta}, & \text{if } \delta =x^{-k} \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise.} \end{array} \right. \end{align} $$
$$ \begin{align} H^j_{{\mathfrak{Z}}}( H^i_\Psi(D_{N}(\delta)))\cong \left\{ \begin{array}{ll} K t_{LT}^k\mathbf{e}_{\delta}, & \text{if } \delta =x^{-k} \text{ for some } 0\leq k\leq N; \\ 0, & \text{otherwise.} \end{array} \right. \end{align} $$
Remark 4.21. Note that, by the same reasoning, the analogue of Lemma 4.5 (ii) (but in general not (iii)) does also hold for M of the form
![]() $ \mathcal {R}_K^+(\delta )$
or
$ \mathcal {R}_K^+(\delta )$
or
![]() $ LA(o_L)(\delta )$
.
$ LA(o_L)(\delta )$
.
Recall that
![]() $\Sigma _1=\{x^{-i}| i\in \mathbb {N}\}, \Sigma _2=\{x^{i}\chi | i\in \mathbb {N}\}$
and
$\Sigma _1=\{x^{-i}| i\in \mathbb {N}\}, \Sigma _2=\{x^{i}\chi | i\in \mathbb {N}\}$
and
![]() $\Sigma _{gen}=\Sigma _{an}\setminus (\Sigma _1\cup \Sigma _2).$
$\Sigma _{gen}=\Sigma _{an}\setminus (\Sigma _1\cup \Sigma _2).$
Lemma 4.22. The dimensions of the analytic cohomology groups are as follows:
-
(i)
 $\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K^+(\delta ))=\left \{ \begin {array}{ll} 0, & {\delta \not \in \Sigma _1;} \\ 1, & {\delta \in \Sigma _1, j=0;} \\ 2, & {\delta \in \Sigma _1, j=1;} \\ 1, & {\delta \in \Sigma _1, j=2.} \end {array} \right .$
$\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K^+(\delta ))=\left \{ \begin {array}{ll} 0, & {\delta \not \in \Sigma _1;} \\ 1, & {\delta \in \Sigma _1, j=0;} \\ 2, & {\delta \in \Sigma _1, j=1;} \\ 1, & {\delta \in \Sigma _1, j=2.} \end {array} \right .$
-
(ii) For
 $\delta ^{-1}\not \in \Sigma _1$
we have
$\delta ^{-1}\not \in \Sigma _1$
we have
 $\dim _K H^j_{\varphi ,D(\Gamma _L,K)}( LA(o_L)(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 1, & {j=1;} \\ 0, & {j=2.} \end {array} \right .$
$\dim _K H^j_{\varphi ,D(\Gamma _L,K)}( LA(o_L)(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 1, & {j=1;} \\ 0, & {j=2.} \end {array} \right .$
-
(iii) For
 $\delta ^{-1}\in \Sigma _1$
we have
$\delta ^{-1}\in \Sigma _1$
we have
 $\dim _K H^j_{\varphi ,D(\Gamma _L,K)}( LA(o_L)(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 2, & {j=1;} \\ 1, & {j=2.} \end {array} \right .$
$\dim _K H^j_{\varphi ,D(\Gamma _L,K)}( LA(o_L)(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 2, & {j=1;} \\ 1, & {j=2.} \end {array} \right .$
-
(iv) For
 $\delta \in \Sigma _1$
we have
$\delta \in \Sigma _1$
we have
 $\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K(\delta ))=\left \{ \begin {array}{ll} 1, & {j=0;} \\ 2, & {j=1;} \\ 0, & {j=2.} \end {array} \right .$
$\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K(\delta ))=\left \{ \begin {array}{ll} 1, & {j=0;} \\ 2, & {j=1;} \\ 0, & {j=2.} \end {array} \right .$
-
(v) For
 $\delta \in \Sigma _2$
we have
$\delta \in \Sigma _2$
we have
 $\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 2, & {j=1;} \\ 1, & {j=2.} \end {array} \right .$
$\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 2, & {j=1;} \\ 1, & {j=2.} \end {array} \right .$
-
(vi) For
 $\delta \in \Sigma _{gen}$
we have
$\delta \in \Sigma _{gen}$
we have
 $\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 1, & {j=1;} \\ 0, & {j=2.} \end {array} \right .$
$\dim _K H^j_{\varphi ,D(\Gamma _L,K)}(\mathcal {R}_K(\delta ))=\left \{ \begin {array}{ll} 0, & {j=0;} \\ 1, & {j=1;} \\ 0, & {j=2.} \end {array} \right .$
In particular, generic characters are precisely those with vanishing
![]() $H^0$
and
$H^0$
and
![]() $H^2.$
$H^2.$
Proof. By Remark 4.1
![]() $H^\bullet _{an}(A^+,M)$
in [Reference Colmez15, §5] coincides with
$H^\bullet _{an}(A^+,M)$
in [Reference Colmez15, §5] coincides with
![]() $H^\bullet _{\varphi ,D(\Gamma _L,K)}(M).$
Note that Colmez uses L to denote a large field such as our field
$H^\bullet _{\varphi ,D(\Gamma _L,K)}(M).$
Note that Colmez uses L to denote a large field such as our field
![]() $K.$
$K.$
It is easy to check that analogous results as in this subsection hold for modules of the form
![]() $\mathcal {R}_A(\delta )$
for affinoids A over K instead of the base field K. The only subtlety is the appearance of non-trivial zero divisors. By imposing some additional conditions we can strengthen 4.9 to cover the affinoid case as well.
$\mathcal {R}_A(\delta )$
for affinoids A over K instead of the base field K. The only subtlety is the appearance of non-trivial zero divisors. By imposing some additional conditions we can strengthen 4.9 to cover the affinoid case as well.
Note that the action of
![]() $\Gamma _L$
on
$\Gamma _L$
on
![]() $A(\delta \chi _{LT}^{\pm i})$
extends to an action of
$A(\delta \chi _{LT}^{\pm i})$
extends to an action of
![]() $D(\Gamma _L,K)$
by continuity. The element
$D(\Gamma _L,K)$
by continuity. The element
![]() $\mathfrak {Z}$
acts as an A-linear endomorphism on
$\mathfrak {Z}$
acts as an A-linear endomorphism on
![]() $A(\delta \chi _{LT}^{\pm i})$
hence by multiplication with an element
$A(\delta \chi _{LT}^{\pm i})$
hence by multiplication with an element
![]() $\mathfrak {Z}(\delta \chi _{LT}^{\pm i}) \in A.$
$\mathfrak {Z}(\delta \chi _{LT}^{\pm i}) \in A.$
Remark 4.23.
-
(i) Let A be affinoid over K and let
 $\delta \colon L^\times \to A^\times $
be a locally L-analytic character. Assume that
$\delta \colon L^\times \to A^\times $
be a locally L-analytic character. Assume that
 $1-\delta (\pi )\pi ^i$
is not a non-trivial zero divisor in A for every
$1-\delta (\pi )\pi ^i$
is not a non-trivial zero divisor in A for every
 $i \in \mathbb {Z}$
and assume that (the image of)
$i \in \mathbb {Z}$
and assume that (the image of)
 $\mathfrak {Z}(\delta \chi _{LT}^{\pm i}) \in A$
is not a non-trivial zero divisor in A or any
$\mathfrak {Z}(\delta \chi _{LT}^{\pm i}) \in A$
is not a non-trivial zero divisor in A or any
 $A/(1-\delta (\pi )\pi ^i)$
Footnote
16
. Then
$A/(1-\delta (\pi )\pi ^i)$
Footnote
16
. Then
 $\mathcal {T}_{\Psi }(M)$
is perfect as a
$\mathcal {T}_{\Psi }(M)$
is perfect as a
 $D(\Gamma _L,A)$
-module for M in
$D(\Gamma _L,A)$
-module for M in  $$\begin{align*}\{\mathcal{R}_A^{+}(\delta), \mathcal{R}_A(\delta), LA(o_L,A)(\delta\chi^{-1}), D_{A,N}(\delta), Pol_{\leq N}(o_L,A)(\chi^{-1}\delta) \}.\end{align*}$$
$$\begin{align*}\{\mathcal{R}_A^{+}(\delta), \mathcal{R}_A(\delta), LA(o_L,A)(\delta\chi^{-1}), D_{A,N}(\delta), Pol_{\leq N}(o_L,A)(\chi^{-1}\delta) \}.\end{align*}$$
-
(ii) As in Nakamura’s setting we expect the statement of (i) to be true without any condition. Unfortunately, the methods of [Reference Kedlaya, Pottharst and Xiao28, Section 5] do not transfer to our situation directly due to the fact that [Reference Kedlaya, Pottharst and Xiao28] makes use of the Euler characteristic formula and perfectness of the
 $\Psi $
-complex in the étale case. The analogues of these results are not known to us for analytic cohomology over affinoids.
$\Psi $
-complex in the étale case. The analogues of these results are not known to us for analytic cohomology over affinoids.
Proof. First observe that for any locally analytic character
![]() $\rho \colon L^\times \to A^\times $
the free rank one module
$\rho \colon L^\times \to A^\times $
the free rank one module
![]() $A(\rho )$
is perfect as a
$A(\rho )$
is perfect as a
![]() $D(U,A)$
-module if
$D(U,A)$
-module if
![]() $\mathfrak {Z}(\rho )$
is not a non-trivial zero divisor in
$\mathfrak {Z}(\rho )$
is not a non-trivial zero divisor in
![]() $A.$
Indeed, let
$A.$
Indeed, let
![]() $\alpha :=\mathfrak {Z}(\rho ) \in A.$
Then, using the assumptions on
$\alpha :=\mathfrak {Z}(\rho ) \in A.$
Then, using the assumptions on
![]() $\alpha ,$
one sees that
$\alpha ,$
one sees that
![]() $A(\rho ) \cong D(U,A)/(\mathfrak {Z}-\alpha )D(U,A)$
is perfect as a
$A(\rho ) \cong D(U,A)/(\mathfrak {Z}-\alpha )D(U,A)$
is perfect as a
![]() $D(U,A)$
-module but then also perfect as a
$D(U,A)$
-module but then also perfect as a
![]() $D(\Gamma _L,A)$
-module by [Reference Steingart51, Lemma 2.5]. Let us call a module of the form
$D(\Gamma _L,A)$
-module by [Reference Steingart51, Lemma 2.5]. Let us call a module of the form
![]() $A(\rho )$
of type
$A(\rho )$
of type
![]() $\mathcal {F}$
. Now consider the sequence
$\mathcal {F}$
. Now consider the sequence
We have that
![]() $\mathcal {T}_{\Psi }(LA(o_L,A)(\chi ^{-1}\delta ))$
is perfect by [48, Tag 066T] since the inclusion of the
$\mathcal {T}_{\Psi }(LA(o_L,A)(\chi ^{-1}\delta ))$
is perfect by [48, Tag 066T] since the inclusion of the
![]() $Pol_{\leq N}(o_L,A)(\chi ^{-1}\delta )$
induces a quasi-isomorphism for
$Pol_{\leq N}(o_L,A)(\chi ^{-1}\delta )$
induces a quasi-isomorphism for
![]() $N \gg 0$
to a complex whose terms are perfect as they are finite direct sums of modules of type
$N \gg 0$
to a complex whose terms are perfect as they are finite direct sums of modules of type
![]() $\mathcal {F}$
. Similarly for
$\mathcal {F}$
. Similarly for
![]() $D_{A,N}(\delta ).$
To see that
$D_{A,N}(\delta ).$
To see that
![]() $\mathcal {R}_A^+(\delta )^{\Psi =1}$
is perfect, consider the exact sequence
$\mathcal {R}_A^+(\delta )^{\Psi =1}$
is perfect, consider the exact sequence
where
![]() $V_1,V_2$
are defined as kernel and co-kernel of the middle map. By an adaptation of [Reference Chenevier11, Lemma 2.9 and Proposition 2.20] to our situation the kernel is of type
$V_1,V_2$
are defined as kernel and co-kernel of the middle map. By an adaptation of [Reference Chenevier11, Lemma 2.9 and Proposition 2.20] to our situation the kernel is of type
![]() $\mathcal {F}$
over A while the cokernel is a finite direct sum of modules of type
$\mathcal {F}$
over A while the cokernel is a finite direct sum of modules of type
![]() $\mathcal {F}$
over
$\mathcal {F}$
over
![]() $A/(1-\delta (\pi )\pi ^i)$
with varying
$A/(1-\delta (\pi )\pi ^i)$
with varying
![]() $i.$
It suffices to see that they are perfect as
$i.$
It suffices to see that they are perfect as
![]() $D(\Gamma _L,A)$
-modules. This follows from the assumption that
$D(\Gamma _L,A)$
-modules. This follows from the assumption that
![]() $(1-\delta (\pi )\pi ^i)$
is not a zero divisor and hence
$(1-\delta (\pi )\pi ^i)$
is not a zero divisor and hence
![]() $D(\Gamma _L,A/(1-\delta (\pi )\pi ^i))$
is itself perfect as a
$D(\Gamma _L,A/(1-\delta (\pi )\pi ^i))$
is itself perfect as a
![]() $D(\Gamma _L,A)$
-module. It remains to see that
$D(\Gamma _L,A)$
-module. It remains to see that
![]() $\mathcal {R}_A^+(\delta )/(\Psi -1)$
is perfect. Again by a similar argument it is a finite direct sum of perfect
$\mathcal {R}_A^+(\delta )/(\Psi -1)$
is perfect. Again by a similar argument it is a finite direct sum of perfect
![]() $D(\Gamma _L,A/(1-\delta (\pi )^{-1}\pi ^i))$
modules (the appearance of
$D(\Gamma _L,A/(1-\delta (\pi )^{-1}\pi ^i))$
modules (the appearance of
![]() $\delta (\pi )^{-1}$
is due to using
$\delta (\pi )^{-1}$
is due to using
![]() $\Psi -1$
instead of
$\Psi -1$
instead of
![]() $\varphi -1$
). Our assumptions ensure that
$\varphi -1$
). Our assumptions ensure that
![]() $1-\delta (\pi )^{-1}\pi ^i = (-\delta (\pi )^{-1}\pi ^i)(1-\delta (\pi )\pi ^{-i})$
is not a zero divisor and we can proceed as before. This proves the perfectness of
$1-\delta (\pi )^{-1}\pi ^i = (-\delta (\pi )^{-1}\pi ^i)(1-\delta (\pi )\pi ^{-i})$
is not a zero divisor and we can proceed as before. This proves the perfectness of
![]() $\mathcal {T}_{\Psi }(\mathcal {R}_A(\delta )^+).$
Finally the perfectness of
$\mathcal {T}_{\Psi }(\mathcal {R}_A(\delta )^+).$
Finally the perfectness of
![]() $\mathcal {T}_{\Psi }(\mathcal {R}_A(\delta ))$
follows from the exact sequence (37).
$\mathcal {T}_{\Psi }(\mathcal {R}_A(\delta ))$
follows from the exact sequence (37).
5 Bloch–Kato exponential for analytic
 $(\varphi _L,\Gamma _L)$
-modules
$(\varphi _L,\Gamma _L)$
-modules
Recall that for a module M over a commutative ring R and
![]() $t\in R$
a non-zerodivisor, we use the notation
$t\in R$
a non-zerodivisor, we use the notation
![]() $M_t$
for the localisation of M at the multiplicatively closed subset
$M_t$
for the localisation of M at the multiplicatively closed subset
![]() $\{t^n\}_{n\geq 0}$
.
$\{t^n\}_{n\geq 0}$
.
5.1
 $D_{dR}$
and
$D_{dR}$
and
 $D_{cris}$
for analytic
$D_{cris}$
for analytic
 $(\varphi _L,\Gamma _L)$
-modules
$(\varphi _L,\Gamma _L)$
-modules
In this section we will define versions of
![]() $D_{dR}$
and
$D_{dR}$
and
![]() $D_{cris}$
for L-analytic
$D_{cris}$
for L-analytic
![]() $(\varphi _L, \Gamma _L)$
-modules M. The idea is that, for an étale
$(\varphi _L, \Gamma _L)$
-modules M. The idea is that, for an étale
![]() $(\varphi _L, \Gamma _L)$
-module attached to a representation V, these versions correspond to the identity component of the full
$(\varphi _L, \Gamma _L)$
-module attached to a representation V, these versions correspond to the identity component of the full
![]() $D_{dR}(V)$
, which arise as
$D_{dR}(V)$
, which arise as
![]() $(B_{dR}\otimes _L V)^{G_L}$
instead of
$(B_{dR}\otimes _L V)^{G_L}$
instead of
![]() $(B_{dR}\otimes _{\mathbb {Q}_p} V)^{G_L}$
, and similarly for
$(B_{dR}\otimes _{\mathbb {Q}_p} V)^{G_L}$
, and similarly for
![]() $D_{cris}(V)$
. The comparison between the definitions used in this article and Fontaine’s classical ones is described in [Reference Porat38, Section 5.2].
$D_{cris}(V)$
. The comparison between the definitions used in this article and Fontaine’s classical ones is described in [Reference Porat38, Section 5.2].
Definition 5.1. For an L-analytic
![]() $(\varphi _L, \Gamma _L)$
-module M over
$(\varphi _L, \Gamma _L)$
-module M over
![]() $\mathcal {R}_F$
, we define
$\mathcal {R}_F$
, we define
and
Remark 5.2. Let M be an L-analytic
![]() $(\varphi _L, \Gamma _L)$
-module M over
$(\varphi _L, \Gamma _L)$
-module M over
![]() $\mathcal {R}_L.$
Then
$\mathcal {R}_L.$
Then
![]() $\mathbf {D}_{\mathrm {dR}}(M)$
and
$\mathbf {D}_{\mathrm {dR}}(M)$
and
![]() $\mathbf {D}_{\mathrm {cris}}(M)$
are finite dimensional L-vector spaces of dimension
$\mathbf {D}_{\mathrm {cris}}(M)$
are finite dimensional L-vector spaces of dimension
![]() $\leq \operatorname {rk}(M)$
. Furthermore
$\leq \operatorname {rk}(M)$
. Furthermore
![]() $\varphi _M$
induces an automorphism of
$\varphi _M$
induces an automorphism of
![]() $\mathbf {D}_{\mathrm {cris}}(M).$
$\mathbf {D}_{\mathrm {cris}}(M).$
Proof. We first show that
![]() $\mathbf {D}_{\mathrm {dR}}(M)$
is finite dimensional. By construction
$\mathbf {D}_{\mathrm {dR}}(M)$
is finite dimensional. By construction
![]() $D:=\mathbf {D}_{\text {dif}}(M)$
is a finite-dimensional
$D:=\mathbf {D}_{\text {dif}}(M)$
is a finite-dimensional
![]() $B:=\bigcup _{n\geq 0}L_{n}((t_{LT}))$
-semilinear representation of
$B:=\bigcup _{n\geq 0}L_{n}((t_{LT}))$
-semilinear representation of
![]() $\Gamma _L.$
We claim that the natural map
$\Gamma _L.$
We claim that the natural map
is injective and
![]() $B^{\Gamma _L}=L,$
which shows
$B^{\Gamma _L}=L,$
which shows
![]() $\dim _L(D^{\Gamma _L}) \leq \dim _B(D) =\operatorname {rk}(M)$
. We first show
$\dim _L(D^{\Gamma _L}) \leq \dim _B(D) =\operatorname {rk}(M)$
. We first show
![]() $B^{\Gamma _L}=L.$
Let
$B^{\Gamma _L}=L.$
Let
![]() $f = \sum a_i t_{LT}^i \in B^{\Gamma _L}.$
We conclude
$f = \sum a_i t_{LT}^i \in B^{\Gamma _L}.$
We conclude
![]() $a_i= \chi _{LT}(\gamma )^i\gamma (a_i)$
for every
$a_i= \chi _{LT}(\gamma )^i\gamma (a_i)$
for every
![]() $\gamma \in \Gamma _L.$
Let n be large enough such that all
$\gamma \in \Gamma _L.$
Let n be large enough such that all
![]() $a_i$
belong to
$a_i$
belong to
![]() $L_n.$
Then
$L_n.$
Then
![]() $\gamma (a_i)=a_i$
for every
$\gamma (a_i)=a_i$
for every
![]() $\gamma \in \Gamma _n$
and we conclude that
$\gamma \in \Gamma _n$
and we conclude that
![]() $a_i=0$
holds for every
$a_i=0$
holds for every
![]() $i \neq 0.$
Finally
$i \neq 0.$
Finally
![]() $\gamma (a_0) \in L_n^{\Gamma _L} = L$
which proves the claim. For the injectivity we argue like in the proof of 2.13 in [Reference Fontaine and Ouyang20]. Consider L-linearly independent vectors
$\gamma (a_0) \in L_n^{\Gamma _L} = L$
which proves the claim. For the injectivity we argue like in the proof of 2.13 in [Reference Fontaine and Ouyang20]. Consider L-linearly independent vectors
![]() $v_1,\dots ,v_d\in D^{\Gamma _L}$
such that
$v_1,\dots ,v_d\in D^{\Gamma _L}$
such that
 $$ \begin{align*}\sum_{i=1}^d \lambda_iv_i=0\end{align*} $$
$$ \begin{align*}\sum_{i=1}^d \lambda_iv_i=0\end{align*} $$
with some
![]() $\lambda _i \in B.$
Suppose
$\lambda _i \in B.$
Suppose
![]() $d \geq 2, \lambda _1 \neq 0 $
and assume without loss of generality
$d \geq 2, \lambda _1 \neq 0 $
and assume without loss of generality
![]() $\lambda _1=1.$
We obtain
$\lambda _1=1.$
We obtain
![]() $v_1 = \gamma (v_1) = \sum _{i=2}^d- \gamma (\lambda _i)v_i.$
Arguing by induction we may assume that
$v_1 = \gamma (v_1) = \sum _{i=2}^d- \gamma (\lambda _i)v_i.$
Arguing by induction we may assume that
![]() $v_2,\dots ,v_d$
are linearly independent over B and conclude
$v_2,\dots ,v_d$
are linearly independent over B and conclude
![]() $\lambda _2,\dots ,\lambda _d \in B^{\Gamma _L}=L$
, a contradiction. From the injectivity of
$\lambda _2,\dots ,\lambda _d \in B^{\Gamma _L}=L$
, a contradiction. From the injectivity of
![]() $\iota _n$
according to Remark 3.14 we deduce that
$\iota _n$
according to Remark 3.14 we deduce that
![]() $\dim _L(\mathbf {D}_{\mathrm {cris}}(M)) \leq \dim _L(\mathbf {D}_{\mathrm {dR}}(M)).$
Finally
$\dim _L(\mathbf {D}_{\mathrm {cris}}(M)) \leq \dim _L(\mathbf {D}_{\mathrm {dR}}(M)).$
Finally
![]() $\varphi _M$
induces an injective endomorphism of
$\varphi _M$
induces an injective endomorphism of
![]() $M_{t_{LT}}$
and by a dimension argument an automorphism of
$M_{t_{LT}}$
and by a dimension argument an automorphism of
![]() $\mathbf {D}_{\mathrm {cris}}(M).$
$\mathbf {D}_{\mathrm {cris}}(M).$
5.2
 $\exp $
for analytic
$\exp $
for analytic
 $(\varphi _L,\Gamma _L)$
-modules
$(\varphi _L,\Gamma _L)$
-modules
Let M be an L-analytic
![]() $(\varphi _L, \Gamma _L)$
-module over
$(\varphi _L, \Gamma _L)$
-module over
![]() $\mathcal {R}_K$
. By Prop. 3.18, we have an action of
$\mathcal {R}_K$
. By Prop. 3.18, we have an action of
![]() $D(\Gamma ,K)$
on M. Thus we may (for some fixed n) consider the complex
$D(\Gamma ,K)$
on M. Thus we may (for some fixed n) consider the complex
![]() $K_{\varphi ,{\mathfrak {Z}}_n}(M)$
, which (up to sign) amounts to
$K_{\varphi ,{\mathfrak {Z}}_n}(M)$
, which (up to sign) amounts to
concentrated in degree
![]() $[0,2]$
.
$[0,2]$
.
On the other hand, for any
![]() $D(\Gamma ,K)$
-module N, we define
$D(\Gamma ,K)$
-module N, we define
concentrated in degree
![]() $[0,1]$
, and denote its cohomology by
$[0,1]$
, and denote its cohomology by
![]() $H^\bullet _{{\mathfrak {Z}}_n}(N)$
.
$H^\bullet _{{\mathfrak {Z}}_n}(N)$
.
Next we want to define
![]() $K^{(\varphi )}_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
and
$K^{(\varphi )}_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
and
![]() $K^{(\varphi )}_{{\mathfrak {Z}}_n}(M_0)$
for
$K^{(\varphi )}_{{\mathfrak {Z}}_n}(M_0)$
for
![]() $M_0 \in \{M, M_{t_{LT}}\}$
. By inspecting the proof in the reference for Prop. 3.18, one sees that the action of
$M_0 \in \{M, M_{t_{LT}}\}$
. By inspecting the proof in the reference for Prop. 3.18, one sees that the action of
![]() $D(\Gamma ,K)$
on M preserves all the
$D(\Gamma ,K)$
on M preserves all the
![]() $M^{(m)}$
. For
$M^{(m)}$
. For
![]() $m \gg 0$
, we set
$m \gg 0$
, we set
concentrated in degree
![]() $[0,2]$
. Passing to the limit with respect to the transition maps induced by the canonical inclusions
$[0,2]$
. Passing to the limit with respect to the transition maps induced by the canonical inclusions ![]() recovers
recovers
![]() $K_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
, but taking the limit with respect to the transition maps induced by
$K_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
, but taking the limit with respect to the transition maps induced by
![]() $\varphi \colon M_0^{(m)} \longrightarrow M_0^{(m+1)}$
produces a new complex
$\varphi \colon M_0^{(m)} \longrightarrow M_0^{(m+1)}$
produces a new complex
whose cohomology we denote by
![]() $H^{(\varphi ),\bullet }_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
. Similarly we define
$H^{(\varphi ),\bullet }_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
. Similarly we define
with cohomology groups denoted by
![]() $H^{(\varphi ),\bullet }_{{\mathfrak {Z}}_n}(M_0)$
.
$H^{(\varphi ),\bullet }_{{\mathfrak {Z}}_n}(M_0)$
.
Remark 5.3. Note that we have
and
Lemma 5.4. For
![]() $m \gg 0$
and
$m \gg 0$
and
![]() $M_0 \in \{M, M[1/t_{LT}]\}$
, the following natural maps induced by
$M_0 \in \{M, M[1/t_{LT}]\}$
, the following natural maps induced by
![]() $\varphi $
are quasi-isomorphisms:
$\varphi $
are quasi-isomorphisms:
 $$ \begin{align*} &K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif},m}^{(+)}(M)) \longrightarrow K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif},m+1}^{(+)}(M)),\\ &K_{{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow K_{{\mathfrak{Z}}_n}(M_0^{(m+1)}) \text{ and } \\ &\widetilde{K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow \widetilde{K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m+1)}) \end{align*} $$
$$ \begin{align*} &K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif},m}^{(+)}(M)) \longrightarrow K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif},m+1}^{(+)}(M)),\\ &K_{{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow K_{{\mathfrak{Z}}_n}(M_0^{(m+1)}) \text{ and } \\ &\widetilde{K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow \widetilde{K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m+1)}) \end{align*} $$
In particular, the maps
 $$ \begin{align*} &K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif},m}^{(+)}(M)) \longrightarrow K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif}}^{(+)}(M)), \\ &K_{{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow K^{(\varphi)}_{{\mathfrak{Z}}_n}(M_0) \text{ and } \\ &{\widetilde K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow { K}^{(\varphi)}_{\varphi,{\mathfrak{Z}}_n}(M_0) \end{align*} $$
$$ \begin{align*} &K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif},m}^{(+)}(M)) \longrightarrow K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\text{dif}}^{(+)}(M)), \\ &K_{{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow K^{(\varphi)}_{{\mathfrak{Z}}_n}(M_0) \text{ and } \\ &{\widetilde K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow { K}^{(\varphi)}_{\varphi,{\mathfrak{Z}}_n}(M_0) \end{align*} $$
are quasi-isomorphisms.
Proof. We only need prove the first statement.By Lemma 4.4 the action of
![]() $\mathfrak {Z}_n$
on
$\mathfrak {Z}_n$
on
![]() $M_0^{\psi =0}$
(resp.
$M_0^{\psi =0}$
(resp.
![]() $(M_0^{(m)})^{\psi =0}$
) is invertible. Using this fact, one can conclude the proof with the same (purely formal) arguments as in the proof of [Reference Nakamura36, Lemma 2.17].
$(M_0^{(m)})^{\psi =0}$
) is invertible. Using this fact, one can conclude the proof with the same (purely formal) arguments as in the proof of [Reference Nakamura36, Lemma 2.17].
Lemma 5.5.
-
(i) For
 $m \gg 0$
and
$m \gg 0$
and
 $M_0 \in \{M, M_{t_{LT}}\}$
, the map induced by the inclusion
$M_0 \in \{M, M_{t_{LT}}\}$
, the map induced by the inclusion $$ \begin{align*} \widetilde{K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow {K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{}) \end{align*} $$
$$ \begin{align*} \widetilde{K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{(m)}) \longrightarrow {K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{}) \end{align*} $$
 is a quasi-isomorphism.
is a quasi-isomorphism.
-
(ii) In
 $\mathbf {D}^-(K)$
, by composing the inverse of the isomorphism in (i) with the isomorphism
$\mathbf {D}^-(K)$
, by composing the inverse of the isomorphism in (i) with the isomorphism
 $\widetilde {K}_{\varphi ,{\mathfrak {Z}}_n}(M_0^{(m)}) \longrightarrow {K}^{(\varphi )}_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
from Lemma 5.4, one obtains an isomorphism which is independent of the choice of
$\widetilde {K}_{\varphi ,{\mathfrak {Z}}_n}(M_0^{(m)}) \longrightarrow {K}^{(\varphi )}_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
from Lemma 5.4, one obtains an isomorphism which is independent of the choice of $$ \begin{align*} {K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{}) \overset{\sim}{\longrightarrow} {K}^{(\varphi)}_{\varphi,{\mathfrak{Z}}_n}(M_0) \end{align*} $$
$$ \begin{align*} {K}_{\varphi,{\mathfrak{Z}}_n}(M_0^{}) \overset{\sim}{\longrightarrow} {K}^{(\varphi)}_{\varphi,{\mathfrak{Z}}_n}(M_0) \end{align*} $$
 $m \gg 0$
.
$m \gg 0$
.
Proof. Both statements follow by purely formal arguments from Lemma 5.4, just as in the proof of [Reference Nakamura36, Lemma 2.20].
Definition 5.6.
-
(a) By the compatibility of the maps
 $\iota _m$
with
$\iota _m$
with
 $\varphi \colon M^{(m)}\longrightarrow M^{(m+1)}$
and the inclusions
$\varphi \colon M^{(m)}\longrightarrow M^{(m+1)}$
and the inclusions  as in Definition 3.15, the
as in Definition 3.15, the
 $\iota _m$
induce canonical morphismsFootnote
17
which we will both call
$\iota _m$
induce canonical morphismsFootnote
17
which we will both call $$ \begin{align*} K_{\mathfrak{Z}_n}^{(\varphi)}(M)\longrightarrow K_{\mathfrak{Z}_n}(\mathbf{D}_{\mathrm{dif}}^+(M))\ \ \ \ \ \text{and}\ \ \ \ \ K_{\mathfrak{Z}_n}^{(\varphi)}(M_{t_{LT}})\longrightarrow K_{\mathfrak{Z}_n}(\mathbf{D}_{\mathrm{dif}}(M)) \end{align*} $$
$$ \begin{align*} K_{\mathfrak{Z}_n}^{(\varphi)}(M)\longrightarrow K_{\mathfrak{Z}_n}(\mathbf{D}_{\mathrm{dif}}^+(M))\ \ \ \ \ \text{and}\ \ \ \ \ K_{\mathfrak{Z}_n}^{(\varphi)}(M_{t_{LT}})\longrightarrow K_{\mathfrak{Z}_n}(\mathbf{D}_{\mathrm{dif}}(M)) \end{align*} $$
 $\iota $
. Moreover, the inclusions
$\iota $
. Moreover, the inclusions  induce a map
induce a map  $$ \begin{align*} \operatorname{\mathrm{Frob}}\colon K_{{\mathfrak{Z}}_n}^{(\varphi)}(M_0)\longrightarrow K_{{\mathfrak{Z}}_n}^{(\varphi)}(M_0). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Frob}}\colon K_{{\mathfrak{Z}}_n}^{(\varphi)}(M_0)\longrightarrow K_{{\mathfrak{Z}}_n}^{(\varphi)}(M_0). \end{align*} $$
-
(b) We construct morphisms
in the following way: $$ \begin{align*} f_n\colon K_{\varphi,\mathfrak{Z}_n}(M_0)\longrightarrow K_{\mathfrak{Z}_n}^{(\varphi)}(M_0)\ \ \ \ \ \text{and}\ \ \ \ \ g_n\colon K_{\varphi,\mathfrak{Z}_n}(M_0)\longrightarrow K_{\mathfrak{Z}_n}(\mathbf{D}_{\mathrm{dif}}^{(+)}(M)) \end{align*} $$
$$ \begin{align*} f_n\colon K_{\varphi,\mathfrak{Z}_n}(M_0)\longrightarrow K_{\mathfrak{Z}_n}^{(\varphi)}(M_0)\ \ \ \ \ \text{and}\ \ \ \ \ g_n\colon K_{\varphi,\mathfrak{Z}_n}(M_0)\longrightarrow K_{\mathfrak{Z}_n}(\mathbf{D}_{\mathrm{dif}}^{(+)}(M)) \end{align*} $$
Define
 $f_n$
as the composition of the isomorphism
$f_n$
as the composition of the isomorphism
 ${K}_{\varphi ,{\mathfrak {Z}}_n}(M_0^{}) \overset {\sim }{\longrightarrow } {K}^{(\varphi )}_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
from Lemma 5.5(ii) with the map
${K}_{\varphi ,{\mathfrak {Z}}_n}(M_0^{}) \overset {\sim }{\longrightarrow } {K}^{(\varphi )}_{\varphi ,{\mathfrak {Z}}_n}(M_0)$
from Lemma 5.5(ii) with the map
 $K_{\varphi ,\mathfrak {Z}_n}^{(\varphi )} (M_0)\longrightarrow K_{\mathfrak {Z}_n}^{(\varphi )}(M_0)$
obtained by taking the direct limit of the morphisms Furthermore, the morphism
$K_{\varphi ,\mathfrak {Z}_n}^{(\varphi )} (M_0)\longrightarrow K_{\mathfrak {Z}_n}^{(\varphi )}(M_0)$
obtained by taking the direct limit of the morphisms Furthermore, the morphism
 $g_n$
is defined as
$g_n$
is defined as  $$ \begin{align*} g_n\colon K_{\varphi,{\mathfrak{Z}}_n}(M_0)\overset {f_n}\longrightarrow K_{{\mathfrak{Z}}_n}^{(\varphi)}(M_0)\overset \iota\longrightarrow K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\mathrm{dif}}^{(+)}(M)). \end{align*} $$
$$ \begin{align*} g_n\colon K_{\varphi,{\mathfrak{Z}}_n}(M_0)\overset {f_n}\longrightarrow K_{{\mathfrak{Z}}_n}^{(\varphi)}(M_0)\overset \iota\longrightarrow K_{{\mathfrak{Z}}_n}(\mathbf{D}_{\mathrm{dif}}^{(+)}(M)). \end{align*} $$
Proposition 5.7. Consider the following diagram:

where the
![]() $d_i$
are given by
$d_i$
are given by
 $$ \begin{align*} & d_1(x):=(x,g_n(x)), && d_2(x,y):=g_n(x)-y,\\ & d_3(x):=(f_n(x),g_n(x)), && d_4(x,y):= (\operatorname{\mathrm{Frob}}(x)-x,\iota(x)-y). \end{align*} $$
$$ \begin{align*} & d_1(x):=(x,g_n(x)), && d_2(x,y):=g_n(x)-y,\\ & d_3(x):=(f_n(x),g_n(x)), && d_4(x,y):= (\operatorname{\mathrm{Frob}}(x)-x,\iota(x)-y). \end{align*} $$
Then the vertical map is a morphism between two distinguished triangles.
Proof. The proof can be carried out analogously to the proof of [Reference Nakamura36, Prop. 2.21]: We make use of the following well-known fact from homological algebra (see for instance [Reference Weibel56, Ex. 10.4.9]):
Let A be a ring and
an exact sequence of complexes of A-modules. Then there exists a natural map
![]() $Z^\bullet \longrightarrow X^\bullet [1]$
in the derived category
$Z^\bullet \longrightarrow X^\bullet [1]$
in the derived category
![]() $\mathbf {D}(A)$
such that
$\mathbf {D}(A)$
such that
is a distinguished triangle.
First, we show that the upper row is a distinguished triangle. Our goal is to replace the complexes
![]() $K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif}}^{(+)}(M))$
by new, quasi-isomorphic complexes
$K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif}}^{(+)}(M))$
by new, quasi-isomorphic complexes
![]() $\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif}}^{(+)}(M))$
, which we define below, and construct an exact sequence
$\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif}}^{(+)}(M))$
, which we define below, and construct an exact sequence
that will induce the upper triangle in the statement by the above-stated fact. For
![]() $k\geq 0$
and
$k\geq 0$
and
![]() $m\gg 0$
, we put
$m\gg 0$
, we put
and denote by
![]() $\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(t_{LT}^{-k}\cdot \mathbf {D}_{\operatorname {\mathrm {dif}},m}^+ (M))$
the complex concentrated in degree
$\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(t_{LT}^{-k}\cdot \mathbf {D}_{\operatorname {\mathrm {dif}},m}^+ (M))$
the complex concentrated in degree
![]() $[0,2]$
:
$[0,2]$
:
where
and
Furthermore, let
We now define
as the sequence of complexes induced by applying
![]() $\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(-)$
to
$\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(-)$
to
where
Down below, the sequence (38) will be obtained as a direct limit of the sequences (39). We claim that the sequence (40) and hence also (39) is exact. Consequently, the same will then hold for the direct limit (38).
The crucial part now is the exactness of (40), which generalizes the exactness of the sequence (5) in the proof of [Reference Nakamura36, Prop. 2.21]. The latter is demonstrated in [Reference Nakamura35, Lem. 2.9], and we check that the arguments carry over to our sequence (40). The non-trivial statements are
![]() $\ker (c_2)=\operatorname {im}(c_1)$
and the surjectivity of
$\ker (c_2)=\operatorname {im}(c_1)$
and the surjectivity of
![]() $c_2$
.
$c_2$
.
The second statement can be reduced to showing that the map
is surjective, using the fact that
![]() $M_{t_{LT}}^{(m)} =\bigcup _{k\geq 0}t_{LT}^{-k}M^{(m)}$
and reducing inductively to the case
$M_{t_{LT}}^{(m)} =\bigcup _{k\geq 0}t_{LT}^{-k}M^{(m)}$
and reducing inductively to the case
![]() $k=1$
via dévissage. Now we fix an
$k=1$
via dévissage. Now we fix an
![]() $\mathcal {R}_F^{(m)}$
-basis
$\mathcal {R}_F^{(m)}$
-basis
![]() $e_1,\ldots ,e_d$
of
$e_1,\ldots ,e_d$
of
![]() $M^{(m)}$
, assuming m is large enough for Proposition 3.2 to hold. From [Reference Berger3, Prop. 4.8 & Lem. 4.9] it follows that for any
$M^{(m)}$
, assuming m is large enough for Proposition 3.2 to hold. From [Reference Berger3, Prop. 4.8 & Lem. 4.9] it follows that for any
![]() $\mu \geq m$
, the composition
$\mu \geq m$
, the composition
induces an isomorphism
![]() $\mathcal {R}_L^{(m)}/(Q_\mu )\cong L_\mu $
where
$\mathcal {R}_L^{(m)}/(Q_\mu )\cong L_\mu $
where
![]() $Q_\mu :=\frac {\varphi ^\mu (Z)}{\varphi ^{\mu -1}(Z)}$
.Footnote
18
Therefore, using [Reference Schneider and Venjakob46, Lemma 4.3.6], we obtain on the level of the extension F an isomorphism
$Q_\mu :=\frac {\varphi ^\mu (Z)}{\varphi ^{\mu -1}(Z)}$
.Footnote
18
Therefore, using [Reference Schneider and Venjakob46, Lemma 4.3.6], we obtain on the level of the extension F an isomorphism
for
![]() $\mu \geq m$
. As a result, we see that
$\mu \geq m$
. As a result, we see that
![]() $(\overline {\iota _\mu (e_i)})_{i=1,\ldots ,d}$
is an
$(\overline {\iota _\mu (e_i)})_{i=1,\ldots ,d}$
is an
![]() $F_\mu $
-basis of
$F_\mu $
-basis of
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}},\mu }^+(M) /t_{LT}$
for any
$\mathbf {D}_{\operatorname {\mathrm {dif}},\mu }^+(M) /t_{LT}$
for any
![]() $\mu \geq m$
. Now the surjectivity of (41) is proven just as in [Reference Nakamura35, Lem. 2.9]: For a family
$\mu \geq m$
. Now the surjectivity of (41) is proven just as in [Reference Nakamura35, Lem. 2.9]: For a family
![]() $(y_\mu )_{\mu \geq m}$
in the target, we write
$(y_\mu )_{\mu \geq m}$
in the target, we write
![]() $y_\mu = \sum _{i=1}^da_{\mu ,i}\cdot \overline {\iota _\mu ( e_i)}$
for
$y_\mu = \sum _{i=1}^da_{\mu ,i}\cdot \overline {\iota _\mu ( e_i)}$
for
![]() $\mu \geq m$
. Choosing a representative
$\mu \geq m$
. Choosing a representative
![]() $a_i\in \mathcal {R}_F^{(m)}$
of the preimage of
$a_i\in \mathcal {R}_F^{(m)}$
of the preimage of
![]() $(a_{\mu ,i})_{\mu \geq m}$
under the natural isomorphism
$(a_{\mu ,i})_{\mu \geq m}$
under the natural isomorphism
for each i, we obtain a preimage
![]() $\sum _{i=1}^d a_ie_i$
of
$\sum _{i=1}^d a_ie_i$
of
![]() $(y_\mu )_\mu $
under (41). To see (42) one uses
$(y_\mu )_\mu $
under (41). To see (42) one uses
![]() $t_{LT}=Z\prod _{\mu \geq 1}\frac {Q_\mu } {\pi _L}$
as well as the fact that
$t_{LT}=Z\prod _{\mu \geq 1}\frac {Q_\mu } {\pi _L}$
as well as the fact that
![]() $t_{LT}$
and
$t_{LT}$
and
![]() $\prod _{\mu \geq m}\frac {Q_\mu }{\pi _L}$
differ by a unit in
$\prod _{\mu \geq m}\frac {Q_\mu }{\pi _L}$
differ by a unit in
![]() $\mathcal {R}_F^{(m)}$
since for
$\mathcal {R}_F^{(m)}$
since for
![]() $\nu <m$
the
$\nu <m$
the
![]() $Q_\nu $
are units as they have no zeros inside the annulus of convergence of
$Q_\nu $
are units as they have no zeros inside the annulus of convergence of
![]() $\mathcal {R}_F^{(m)}$
. Now (42) follows via a projective limit argument from the isomorphisms
$\mathcal {R}_F^{(m)}$
. Now (42) follows via a projective limit argument from the isomorphisms
![]() $\mathcal {R}_F^{(m)}/(Q_\mu )\cong F_\mu $
and the Chinese remainder theorem.
$\mathcal {R}_F^{(m)}/(Q_\mu )\cong F_\mu $
and the Chinese remainder theorem.
Concerning the first statement
![]() $\ker (c_2)= \operatorname {im}(c_1)$
, one needs to show for any
$\ker (c_2)= \operatorname {im}(c_1)$
, one needs to show for any
![]() $x\in M^{(m)}_{t_{LT}}$
that if
$x\in M^{(m)}_{t_{LT}}$
that if
![]() $\iota _\mu (x)\in \mathbf {D}_{\operatorname {\mathrm {dif}},\mu }^+(M)$
for all
$\iota _\mu (x)\in \mathbf {D}_{\operatorname {\mathrm {dif}},\mu }^+(M)$
for all
![]() $\mu \geq m$
, then we have in fact
$\mu \geq m$
, then we have in fact
![]() $x\in M^{(m)}$
. Writing
$x\in M^{(m)}$
. Writing
![]() $x=x_0\cdot t_{LT}^{-k}$
with
$x=x_0\cdot t_{LT}^{-k}$
with
![]() $x_0\in M^{(m)}$
, Remark 3.14 implies
$x_0\in M^{(m)}$
, Remark 3.14 implies
 $$ \begin{align*} \iota_\mu(x)=\frac{\iota_\mu(x_0)\cdot \pi_{LT}^{\mu k}}{t_{LT}^k}. \end{align*} $$
$$ \begin{align*} \iota_\mu(x)=\frac{\iota_\mu(x_0)\cdot \pi_{LT}^{\mu k}}{t_{LT}^k}. \end{align*} $$
So the claim follows if we show that if
![]() $t_{LT}^k$
divides
$t_{LT}^k$
divides
![]() $\iota _\mu (x_0)$
in
$\iota _\mu (x_0)$
in
![]() $F_\mu [[t_{LT}]]$
for all
$F_\mu [[t_{LT}]]$
for all
![]() $\mu \geq m$
, then it also divides
$\mu \geq m$
, then it also divides
![]() $x_0$
in
$x_0$
in
![]() $M^{(m)}$
. Of course, we can assume
$M^{(m)}$
. Of course, we can assume
![]() $k=1$
as well as
$k=1$
as well as
![]() $M=\mathcal {R}_F$
after choosing a basis of M. Then the isomorphism (42) yields the desired result.
$M=\mathcal {R}_F$
after choosing a basis of M. Then the isomorphism (42) yields the desired result.
Now that the exactness of (40) is established, it follows by construction that the sequence (39) of complexes is exact as well.
Next we form the direct limit of the sequences (39) over m, where the transition maps are the ones induced by the natural inclusions ![]() and the maps
and the maps
given by “cutting off” the component at the lowest index. So by defining
we obtain the desired exact sequence (38).
This sequence yields a distinguished triangle as explained in the beginning of the proof; in order to bring this triangle into the desired form, it remains to define suitable quasi-isomorphisms of complexes
![]() $K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif}}^{(+)}(M))\longrightarrow \widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif}}^{(+)}(M))$
, which is done in the following way: First, for
$K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif}}^{(+)}(M))\longrightarrow \widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif}}^{(+)}(M))$
, which is done in the following way: First, for
![]() $m\gg 0$
consider the morphisms
$m\gg 0$
consider the morphisms
![]() $K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}^{+}(M))\longrightarrow \widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}^{+}(M))$
defined by
$K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}^{+}(M))\longrightarrow \widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}^{+}(M))$
defined by

noting that
![]() $b_0((x)_{\mu \geq m}) = ((\mathfrak {Z}_nx)_{\mu \geq m}, (x-x)_{\mu \geq {m+1}}) = ((\mathfrak {Z}_nx)_{\mu \geq m}, 0).$
There are similar morphisms
$b_0((x)_{\mu \geq m}) = ((\mathfrak {Z}_nx)_{\mu \geq m}, (x-x)_{\mu \geq {m+1}}) = ((\mathfrak {Z}_nx)_{\mu \geq m}, 0).$
There are similar morphisms
![]() $K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}(M))\longrightarrow \widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}(M))$
, and one checks that they are all quasi-isomorphisms, using the exactness of the sequence
$K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}(M))\longrightarrow \widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}(M))$
, and one checks that they are all quasi-isomorphisms, using the exactness of the sequence
It is obvious that the quasi-isomorphisms
![]() $K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}^{(+)}(M))\overset {\sim }{\longrightarrow }\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}^{(+)}(M))$
are compatible with the transition maps, induced by the inclusions
$K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}^{(+)}(M))\overset {\sim }{\longrightarrow }\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}^{(+)}(M))$
are compatible with the transition maps, induced by the inclusions ![]() on the left and given by the
on the left and given by the
![]() $a^\bullet $
on the right, so they induce a quasi-isomorphism
$a^\bullet $
on the right, so they induce a quasi-isomorphism
Putting everything together, and inspecting the explicit definitions of the morphisms involved, we get that the upper row of the diagram in the statement is in fact a distinguished triangle.
To demonstrate that the second row is also a distinguished triangle, we start again with forming a certain direct limit of the exact sequences (39) of complexes. But this time, instead of the
![]() $a^\bullet $
from above, we define morphisms
$a^\bullet $
from above, we define morphisms
given by shifting
![]() $(x_\mu )_{\mu \geq m}\longmapsto (x_{\mu -1})_{\mu \geq m+1}$
instead of cutting off. Then let
$(x_\mu )_{\mu \geq m}\longmapsto (x_{\mu -1})_{\mu \geq m+1}$
instead of cutting off. Then let
Furthermore, note that the quasi-isomorphisms
![]() $K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}^{(+)}(M))\overset {\sim }{\longrightarrow }\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}^{(+)}(M))$
from (43) also form a morphism of directed systems if we use the
$K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif},m}^{(+)}(M))\overset {\sim }{\longrightarrow }\widetilde K_{\varphi ,{\mathfrak {Z}}_n}(\mathbf {D}_{ \mathrm {dif},m}^{(+)}(M))$
from (43) also form a morphism of directed systems if we use the
![]() $(a')^\bullet $
instead of the
$(a')^\bullet $
instead of the
![]() $a^\bullet $
as transition maps on the right, so they yield a quasi-isomorphism
$a^\bullet $
as transition maps on the right, so they yield a quasi-isomorphism
After these preparations, we consider the chain of quasi-isomorphisms
 $$ \begin{align} &\widetilde K_{\varphi,{\mathfrak{Z}}_n}(M^{(m)})\cong \operatorname{\mathrm{cone}}\left( \widetilde K_{\varphi,{\mathfrak{Z}}_n}(M^{(m)}_{t_{LT}})\oplus\widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}^+_{\operatorname{\mathrm{dif}},m}(M))\longrightarrow \widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}_{\operatorname{\mathrm{dif}},m}(M))\right)[-1]\notag\\ &\cong \operatorname{\mathrm{cone}}\left(K_{{\mathfrak{Z}}_n}(M^{(m)}_{t_{LT}})\oplus \widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}^+_{\operatorname{\mathrm{dif}},m}(M))\longrightarrow K_{{\mathfrak{Z}}_n}(M^{(m+1)}_{t_{LT}})\oplus \widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}_{\operatorname{\mathrm{dif}},m}(M))\right)[-1], \end{align} $$
$$ \begin{align} &\widetilde K_{\varphi,{\mathfrak{Z}}_n}(M^{(m)})\cong \operatorname{\mathrm{cone}}\left( \widetilde K_{\varphi,{\mathfrak{Z}}_n}(M^{(m)}_{t_{LT}})\oplus\widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}^+_{\operatorname{\mathrm{dif}},m}(M))\longrightarrow \widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}_{\operatorname{\mathrm{dif}},m}(M))\right)[-1]\notag\\ &\cong \operatorname{\mathrm{cone}}\left(K_{{\mathfrak{Z}}_n}(M^{(m)}_{t_{LT}})\oplus \widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}^+_{\operatorname{\mathrm{dif}},m}(M))\longrightarrow K_{{\mathfrak{Z}}_n}(M^{(m+1)}_{t_{LT}})\oplus \widetilde K_{\varphi,{\mathfrak{Z}}_n}(\mathbf{D}_{\operatorname{\mathrm{dif}},m}(M))\right)[-1], \end{align} $$
where the first one follows from applying the fact from homological algebra stated at the beginning of the proof to the sequence (39) and the second one is formally obtained by the identity
Taking the direct limit of the quasi-isomorphisms (45) with respect to the transition maps
![]() $(a')^\bullet $
and the morphisms induced by
$(a')^\bullet $
and the morphisms induced by ![]() , and applying the quasi-isomorphism
, and applying the quasi-isomorphism
![]() $K_{\varphi ,{\mathfrak {Z}}_n}(M) \cong K_{\varphi ,{\mathfrak {Z}}_n}^{(\varphi )}(M)$
from Lemma 5.5(ii) to the left-hand side and (44) to right-hand side, we obtain the distinguished triangle
$K_{\varphi ,{\mathfrak {Z}}_n}(M) \cong K_{\varphi ,{\mathfrak {Z}}_n}^{(\varphi )}(M)$
from Lemma 5.5(ii) to the left-hand side and (44) to right-hand side, we obtain the distinguished triangle
which is the bottom row in the statement of the proposition.
We define
For
![]() $m \gg 0$
, the map
$m \gg 0$
, the map
is an isomorphism by Lemma 5.4. Moreover, the inclusions ![]() are isomorphisms by a result analogous to [Reference Nakamura36, Lemma 2.18] which is formally deduced from Lemma 5.4 (and the fact that the cohomologies are finite-dimensional). Thus the above
are isomorphisms by a result analogous to [Reference Nakamura36, Lemma 2.18] which is formally deduced from Lemma 5.4 (and the fact that the cohomologies are finite-dimensional). Thus the above
![]() $\varphi $
can be viewed as an automorphism
$\varphi $
can be viewed as an automorphism
Next we construct two isomorphisms
![]() $j_1, j_2 \colon \mathbf {D}^{(n)}_{\text {cris}}(M) \overset {\sim }{\longrightarrow } H^{(\varphi ),0}_{{\mathfrak {Z}}_n}(M_{t_{LT}})$
making the diagram
$j_1, j_2 \colon \mathbf {D}^{(n)}_{\text {cris}}(M) \overset {\sim }{\longrightarrow } H^{(\varphi ),0}_{{\mathfrak {Z}}_n}(M_{t_{LT}})$
making the diagram

commute, where
![]() $\operatorname {\mathrm {Frob}}$
is induced by the
$\operatorname {\mathrm {Frob}}$
is induced by the
![]() $\operatorname {\mathrm {Frob}}$
in Definition 5.6(a). Let
$\operatorname {\mathrm {Frob}}$
in Definition 5.6(a). Let
where the last map is an isomorphism by Lemma 5.4. Note that
![]() $j_1$
is independent of the choice of
$j_1$
is independent of the choice of
![]() $m \gg 0$
. Finally, we set
$m \gg 0$
. Finally, we set
Additionally, we define
where
![]() $\iota $
is induced by the
$\iota $
is induced by the
![]() $\iota $
in Definition 5.6(a).
$\iota $
in Definition 5.6(a).
Definition 5.8. Denote by
and
the boundary maps obtained by taking cohomology of the exact triangles in Proposition 5.7.
Set
and
and
Then Proposition 5.7 yields the following diagram with exact rows

where
For later calculations we state the analogue (in the LT-setting) of the
![]() $\mathfrak {f}$
-version (with
$\mathfrak {f}$
-version (with
![]() $\mathfrak {f}\in \{\Psi ,\varphi \}$
) of the explicit formula for
$\mathfrak {f}\in \{\Psi ,\varphi \}$
) of the explicit formula for
![]() $\exp _{M} $
and
$\exp _{M} $
and
![]() $\exp _{f,M} $
in [Reference Nakamura36, Prop. 2.23] and leave the straight forward adaption of the proof to the reader.
$\exp _{f,M} $
in [Reference Nakamura36, Prop. 2.23] and leave the straight forward adaption of the proof to the reader.
Proposition 5.9.
-
(i) For
 $x\in \mathbf {D}^{(n)}_{\text {dR}}(M) $
choose
$x\in \mathbf {D}^{(n)}_{\text {dR}}(M) $
choose
 $\tilde {x}\in M_{t_{\mathrm {LT}}}^{(n')}$
for some sufficiently large
$\tilde {x}\in M_{t_{\mathrm {LT}}}^{(n')}$
for some sufficiently large
 $n'\geq n$
such that for any
$n'\geq n$
such that for any $$\begin{align*}\iota_m(\tilde{x})-x\in \mathbf{D}_{ \mathrm{dif},m}^{+}(M)\end{align*}$$
$$\begin{align*}\iota_m(\tilde{x})-x\in \mathbf{D}_{ \mathrm{dif},m}^{+}(M)\end{align*}$$
 $m\geq n'.$
Then we have
$m\geq n'.$
Then we have  $$ \begin{align*} \exp_M^{(n)}(x)= & [(\mathfrak{f}-1) \tilde{x}, {{\mathfrak{Z}}_n} \tilde{x}]\in H^{1}_{\mathfrak{f},{\mathfrak{Z}}_n}(M). \end{align*} $$
$$ \begin{align*} \exp_M^{(n)}(x)= & [(\mathfrak{f}-1) \tilde{x}, {{\mathfrak{Z}}_n} \tilde{x}]\in H^{1}_{\mathfrak{f},{\mathfrak{Z}}_n}(M). \end{align*} $$
-
(ii) For
 $x\in \mathbf {D}^{(n)}_{\text {dR}}(M) $
choose
$x\in \mathbf {D}^{(n)}_{\text {dR}}(M) $
choose
 $\tilde {x}\in M_{t_{\mathrm {LT}}}^{(n')}$
for some sufficiently large
$\tilde {x}\in M_{t_{\mathrm {LT}}}^{(n')}$
for some sufficiently large
 $n'\geq n$
such that and
$n'\geq n$
such that and $$\begin{align*}\iota_m(\tilde{x}) \in \mathbf{D}_{ \mathrm{dif},n'}^{+}(M)\end{align*}$$
for any
$$\begin{align*}\iota_m(\tilde{x}) \in \mathbf{D}_{ \mathrm{dif},n'}^{+}(M)\end{align*}$$
for any $$\begin{align*}\iota_{n'+k}(\tilde{x})-\sum_{l=1}^{k}\iota_{n'+l}(\varphi^{n'}(x))\in \mathbf{D}_{ \mathrm{dif},n'+k}^{+}(M)\end{align*}$$
$$\begin{align*}\iota_{n'+k}(\tilde{x})-\sum_{l=1}^{k}\iota_{n'+l}(\varphi^{n'}(x))\in \mathbf{D}_{ \mathrm{dif},n'+k}^{+}(M)\end{align*}$$
 $k\geq 1.$
Then we have
$k\geq 1.$
Then we have  $$ \begin{align*} \exp_{f,M}^{(n)}(x)= & [(\varphi-1) \tilde{x}+\varphi^{n'}(x), {{\mathfrak{Z}}_n} \tilde{x}]\in H^{1}_{\varphi,{\mathfrak{Z}}_n}(M). \end{align*} $$
$$ \begin{align*} \exp_{f,M}^{(n)}(x)= & [(\varphi-1) \tilde{x}+\varphi^{n'}(x), {{\mathfrak{Z}}_n} \tilde{x}]\in H^{1}_{\varphi,{\mathfrak{Z}}_n}(M). \end{align*} $$
5.3 Derivatives of measures
In cyclotomic Iwasawa theory the constant
![]() $\log (\chi _{cyc}(\gamma ))$
shows up at various places (see [Reference Nakamura36]) in order to make constructions independent of the choice of a topological generator
$\log (\chi _{cyc}(\gamma ))$
shows up at various places (see [Reference Nakamura36]) in order to make constructions independent of the choice of a topological generator
![]() $\gamma $
of
$\gamma $
of
![]() $\Gamma _{\mathbb {Q}_p}.$
Since we have replaced the element
$\Gamma _{\mathbb {Q}_p}.$
Since we have replaced the element
![]() $\gamma -1$
by
$\gamma -1$
by
![]() ${{\mathfrak {Z}}_n}$
we again have to check the dependence on this choice. As our computations below show, the constant
${{\mathfrak {Z}}_n}$
we again have to check the dependence on this choice. As our computations below show, the constant
![]() $\Omega $
plays a role in normalisation and seems conceptually new at a first glance since in the case
$\Omega $
plays a role in normalisation and seems conceptually new at a first glance since in the case
![]() $L=\mathbb {Q}_p$
one can take
$L=\mathbb {Q}_p$
one can take
![]() $\Omega =1.$
But recall that
$\Omega =1.$
But recall that
![]() $\Omega $
is only unique up to units in
$\Omega $
is only unique up to units in
![]() $o_L,$
hence in the cyclotomic case one could just as well take any element of
$o_L,$
hence in the cyclotomic case one could just as well take any element of
![]() $\mathbb {Z}_p^\times .$
Comparing (20) with [Reference Nakamura36, Proposition 5.2] we see that we should take
$\mathbb {Z}_p^\times .$
Comparing (20) with [Reference Nakamura36, Proposition 5.2] we see that we should take
![]() $\Omega _{\mathbb {Q}_p} = \operatorname {log}_0(\chi (\gamma ))^{-1},$
where
$\Omega _{\mathbb {Q}_p} = \operatorname {log}_0(\chi (\gamma ))^{-1},$
where
![]() $\log _0(a):= \log (a)/p^{v_p(\log (a))}.$
We first generalize the derivative of a measure from the cyclotomic case (e.g. [Reference Loeffler, Venjakob and Zerbes34, §2.1]) in a naive way:
$\log _0(a):= \log (a)/p^{v_p(\log (a))}.$
We first generalize the derivative of a measure from the cyclotomic case (e.g. [Reference Loeffler, Venjakob and Zerbes34, §2.1]) in a naive way:
By
![]() $\langle -\rangle :o_L^\times \to 1+\pi _Lo_L$
we denote the projection which is induced by the Teichmüller character
$\langle -\rangle :o_L^\times \to 1+\pi _Lo_L$
we denote the projection which is induced by the Teichmüller character
![]() $\omega :k_L^\times \to o_L^\times .$
Fix
$\omega :k_L^\times \to o_L^\times .$
Fix
![]() $m_0>\frac {e}{p-1}$
and
$m_0>\frac {e}{p-1}$
and
![]() $m_1\geq 0$
such that
$m_1\geq 0$
such that
![]() $\log _p(o_L^\times )\subseteq \pi _L^{-m_1}o_L$
. Then, for
$\log _p(o_L^\times )\subseteq \pi _L^{-m_1}o_L$
. Then, for
![]() $s\in \pi _L^mo_L$
with
$s\in \pi _L^mo_L$
with
![]() $m:=m_0+m_1$
the map
$m:=m_0+m_1$
the map
is well-defined. For
![]() $\lambda \in D(\Gamma _L,K)$
and
$\lambda \in D(\Gamma _L,K)$
and
![]() $f\in C^{an}(\Gamma _L,K)$
we define
$f\in C^{an}(\Gamma _L,K)$
we define
and
This limit exists and we have
using that
![]() $\lim _{0\neq s\rightarrow 0}\frac {\langle \chi _{LT}(\gamma )\rangle ^s-1}{s}=\log (\chi _{LT}(\gamma )).$
As an example one easily sees using Remark 4.3 that the expression
$\lim _{0\neq s\rightarrow 0}\frac {\langle \chi _{LT}(\gamma )\rangle ^s-1}{s}=\log (\chi _{LT}(\gamma )).$
As an example one easily sees using Remark 4.3 that the expression
 $$ \begin{align} \frac{\mathcal{L}_{{{\mathfrak{Z}}_n}}'(\mathbf{1})}{\pi_L^n} \end{align} $$
$$ \begin{align} \frac{\mathcal{L}_{{{\mathfrak{Z}}_n}}'(\mathbf{1})}{\pi_L^n} \end{align} $$
is independent of
![]() $n.$
$n.$
For
![]() $ D(\Gamma _n)$
as at the beginning of subsection 5.2 there is another way of attaching such a derivative better adapted to the Lubin-Tate situation as follows:
$ D(\Gamma _n)$
as at the beginning of subsection 5.2 there is another way of attaching such a derivative better adapted to the Lubin-Tate situation as follows:
By [Reference Schneider and Teitelbaum43, §3, Thm. 3.6] the characters of
![]() $\Gamma _n$
are all of the form
$\Gamma _n$
are all of the form
![]() $\psi _z(\gamma ):=\kappa _z(\ell _n(\gamma ))$
using their notation. For small
$\psi _z(\gamma ):=\kappa _z(\ell _n(\gamma ))$
using their notation. For small
![]() $\gamma $
we have
$\gamma $
we have
and for
![]() $z=\exp _{LT}(\frac {\pi _L^n}{\Omega })$
the characters
$z=\exp _{LT}(\frac {\pi _L^n}{\Omega })$
the characters
![]() $\psi _z$
and
$\psi _z$
and
![]() $ \chi _{LT}$
coincide on an open subgroup of
$ \chi _{LT}$
coincide on an open subgroup of
![]() $\Gamma _L.$
For
$\Gamma _L.$
For
![]() $\lambda \in D(\Gamma _n)$
and
$\lambda \in D(\Gamma _n)$
and
![]() $f\in C^{an}(\Gamma _n,K)$
we may define
$f\in C^{an}(\Gamma _n,K)$
we may define
and
This limit exists and we have
 $$ \begin{align} \mathcal{L}\mathcal{T}_\lambda'(f)=\frac{\Omega}{\pi_L^n}\lambda(\log(\chi_{LT})f) \end{align} $$
$$ \begin{align} \mathcal{L}\mathcal{T}_\lambda'(f)=\frac{\Omega}{\pi_L^n}\lambda(\log(\chi_{LT})f) \end{align} $$
using that
![]() $\lim _{0\neq z\rightarrow 0}\frac {\psi _z(\gamma )-1}{z}=\frac {\Omega }{\pi _L^n}\log (\chi _{LT}(\gamma ))$
as
$\lim _{0\neq z\rightarrow 0}\frac {\psi _z(\gamma )-1}{z}=\frac {\Omega }{\pi _L^n}\log (\chi _{LT}(\gamma ))$
as
![]() $g_{LT}(0)=1$
by (1).
$g_{LT}(0)=1$
by (1).
We conclude this discussion by considering again
![]() $\lambda ={{\mathfrak {Z}}_n}$
and the trivial character
$\lambda ={{\mathfrak {Z}}_n}$
and the trivial character
![]() $f= \mathbf {1}.$
Then
$f= \mathbf {1}.$
Then
![]() $\mathcal {L}\mathcal {T}_{{\mathfrak {Z}}_n}(\mathbf {1},z)={{\mathfrak {Z}}_n}(\psi _z)= z$
by [Reference Schneider and Teitelbaum43, Lem. 4.6], whence
$\mathcal {L}\mathcal {T}_{{\mathfrak {Z}}_n}(\mathbf {1},z)={{\mathfrak {Z}}_n}(\psi _z)= z$
by [Reference Schneider and Teitelbaum43, Lem. 4.6], whence
![]() $\mathcal {L}\mathcal {T}_{{\mathfrak {Z}}_n}(\mathbf {1},0)=0$
and (49) becomes
$\mathcal {L}\mathcal {T}_{{\mathfrak {Z}}_n}(\mathbf {1},0)=0$
and (49) becomes
 $$ \begin{align} 1= \mathcal{L}\mathcal{T}_{{\mathfrak{Z}}_n}'(\mathbf{1})=\frac{\Omega}{\pi_L^n}{{\mathfrak{Z}}_n}(\log(\chi_{LT})) \text{ and } \frac{\mathcal{L}_{{{\mathfrak{Z}}_n}}'(\mathbf{1})}{\pi_L^n}=\frac{1}{\Omega}. \end{align} $$
$$ \begin{align} 1= \mathcal{L}\mathcal{T}_{{\mathfrak{Z}}_n}'(\mathbf{1})=\frac{\Omega}{\pi_L^n}{{\mathfrak{Z}}_n}(\log(\chi_{LT})) \text{ and } \frac{\mathcal{L}_{{{\mathfrak{Z}}_n}}'(\mathbf{1})}{\pi_L^n}=\frac{1}{\Omega}. \end{align} $$
5.4 The dual exponential map
 $\exp ^*$
$\exp ^*$
Let M be a free L-analytic
![]() $(\varphi _L, \Gamma _L)$
-module over
$(\varphi _L, \Gamma _L)$
-module over
![]() $\mathcal {R}_K$
. We say that M is de Rham if the
$\mathcal {R}_K$
. We say that M is de Rham if the
![]() $B = \bigcup _m K_m((t_{LT}))$
-module
$B = \bigcup _m K_m((t_{LT}))$
-module
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)$
is trivial as a
$\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)$
is trivial as a
![]() $(B,\Gamma _L)$
-module. By Galois descent (technically in the form of [48, Tag 0CDR] for the Scheme
$(B,\Gamma _L)$
-module. By Galois descent (technically in the form of [48, Tag 0CDR] for the Scheme
![]() $X = \operatorname {Spec}(K)$
) this is equivalent to
$X = \operatorname {Spec}(K)$
) this is equivalent to
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)$
being trivial as a
$\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)$
being trivial as a
![]() $(B,\Gamma _n)$
-module for some n. Indeed, in this case
$(B,\Gamma _n)$
-module for some n. Indeed, in this case
![]() $\mathbf {D}_{dR}^{(n)}(M)$
is a
$\mathbf {D}_{dR}^{(n)}(M)$
is a
![]() $K\otimes _{L}L_n$
-module with a semi-linear
$K\otimes _{L}L_n$
-module with a semi-linear
![]() $\Gamma _L/\Gamma _n= \operatorname {Gal}(L_n/L)$
-action (which is trivial on K). Note that we have
$\Gamma _L/\Gamma _n= \operatorname {Gal}(L_n/L)$
-action (which is trivial on K). Note that we have
![]() $\dim _K \mathbf {D}^{(n)}_{\text {dR}}(M)=[L_n : L] \cdot r_M$
where
$\dim _K \mathbf {D}^{(n)}_{\text {dR}}(M)=[L_n : L] \cdot r_M$
where
![]() $r_M$
is the rank of M over
$r_M$
is the rank of M over
![]() $\mathcal {R}_K$
and that
$\mathcal {R}_K$
and that
![]() $\mathbf {D}_{dR}^{(n)}(M)$
is in fact free as a
$\mathbf {D}_{dR}^{(n)}(M)$
is in fact free as a
![]() $K \otimes _L L_n$
-module. We denote by
$K \otimes _L L_n$
-module. We denote by
![]() $\delta _{2,M}$
the connecting homomorphism
$\delta _{2,M}$
the connecting homomorphism
obtained from the sequence in 5.7. We define
for the trivial character
![]() $\mathbf {1}.$
We stress that this is compatible with Nakamura’s definition when specializing to the cyclotomic situation.
$\mathbf {1}.$
We stress that this is compatible with Nakamura’s definition when specializing to the cyclotomic situation.
Lemma 5.10. Let M be de Rham. Then the natural map
 $$ \begin{align*}\left(\bigcup_m K_m((t_{LT}))\right)\otimes_{K_n} \mathbf{D}_{dR}^{(n)}(M)\to \mathbf{D}_{\operatorname{\mathrm{dif}}}(M)\end{align*} $$
$$ \begin{align*}\left(\bigcup_m K_m((t_{LT}))\right)\otimes_{K_n} \mathbf{D}_{dR}^{(n)}(M)\to \mathbf{D}_{\operatorname{\mathrm{dif}}}(M)\end{align*} $$
is an isomorphism and the induced map
is an isomorphism. The inverse is induced by sending
![]() $f\otimes d\in K_m((t_{LT}))\otimes _{K_n} \mathbf {D}_{dR}^{(n)}(M)$
to
$f\otimes d\in K_m((t_{LT}))\otimes _{K_n} \mathbf {D}_{dR}^{(n)}(M)$
to
![]() $C_g({{\mathfrak {Z}}_n})^{-1}\frac {1}{[K_m:K_n]}Tr_{K_m/K_n}(f_{|t_{LT}=0})d,$
where by abuse of notation (although
$C_g({{\mathfrak {Z}}_n})^{-1}\frac {1}{[K_m:K_n]}Tr_{K_m/K_n}(f_{|t_{LT}=0})d,$
where by abuse of notation (although
![]() $t_{LT}$
gets inverted!) we denote by
$t_{LT}$
gets inverted!) we denote by
![]() $ f_{|t_{LT}=0}$
the constant term of f with respect to
$ f_{|t_{LT}=0}$
the constant term of f with respect to
![]() $t_{LT}$
.
$t_{LT}$
.
Proof. The first part follows immediately from the definition and implies that
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)$
is isomorphic to the trivial B-semi-linear
$\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)$
is isomorphic to the trivial B-semi-linear
![]() $\Gamma _n$
-representation. For the second statement it thus suffices to consider the rank
$\Gamma _n$
-representation. For the second statement it thus suffices to consider the rank
![]() $1$
case and prove the statement for B itself, namely that the natural map
$1$
case and prove the statement for B itself, namely that the natural map
![]() $B^{\Gamma _n} \to B \to B/{\mathfrak {Z}}_n$
is an isomorphism. Because the
$B^{\Gamma _n} \to B \to B/{\mathfrak {Z}}_n$
is an isomorphism. Because the
![]() $\Gamma $
-action respects the direct product decomposition
$\Gamma $
-action respects the direct product decomposition
![]() $K_m((t_{LT})) \cong \prod _{k \in \mathbb {Z}} K_mt^{k}_{LT}$
and
$K_m((t_{LT})) \cong \prod _{k \in \mathbb {Z}} K_mt^{k}_{LT}$
and
![]() $B^{\Gamma _n} = K_n$
it suffices to show that any Laurent series, whose constant term vanishes, lies in the image of
$B^{\Gamma _n} = K_n$
it suffices to show that any Laurent series, whose constant term vanishes, lies in the image of
![]() ${\mathfrak {Z}}_n$
and that there is an exact sequence of the form
${\mathfrak {Z}}_n$
and that there is an exact sequence of the form
with
![]() $\mathrm {Tr}=\frac {1}{[K_m:K_n]}\mathrm {Tr}_{K_m/K_n} $
by Wedderburn theory. Using the product decomposition it suffices to treat the monomials
$\mathrm {Tr}=\frac {1}{[K_m:K_n]}\mathrm {Tr}_{K_m/K_n} $
by Wedderburn theory. Using the product decomposition it suffices to treat the monomials
![]() $at_{LT}^k$
with some a
$at_{LT}^k$
with some a
![]() $\in K_m.$
Taking
$\in K_m.$
Taking
![]() $1\neq \gamma \in \Gamma _m$
we obtain
$1\neq \gamma \in \Gamma _m$
we obtain
![]() $\gamma (a)=a$
and
$\gamma (a)=a$
and
![]() $\gamma (t_{LT})= \chi _{LT}(\gamma )t_{LT}.$
By construction
$\gamma (t_{LT})= \chi _{LT}(\gamma )t_{LT}.$
By construction
![]() $(\gamma -1)(t_{LT}) = \pi _L^lu t_{LT}$
for some
$(\gamma -1)(t_{LT}) = \pi _L^lu t_{LT}$
for some
![]() $l \in \mathbb {Z}, u\in o_L^{\times }$
and hence
$l \in \mathbb {Z}, u\in o_L^{\times }$
and hence
![]() $(\gamma -1)(at_{LT}\pi _L^{-l}u^{-1}) = a\pi _L^{-l}u^{-1}((\gamma -1)(t_{LT})) = at_{LT}.$
Since
$(\gamma -1)(at_{LT}\pi _L^{-l}u^{-1}) = a\pi _L^{-l}u^{-1}((\gamma -1)(t_{LT})) = at_{LT}.$
Since
![]() $\delta _{\gamma }-1$
is divisible by
$\delta _{\gamma }-1$
is divisible by
![]() ${\mathfrak {Z}}_n$
in
${\mathfrak {Z}}_n$
in
![]() $D(\Gamma _n,K),$
we conclude that
$D(\Gamma _n,K),$
we conclude that
![]() $at^{k}_{LT}$
lies in the image of
$at^{k}_{LT}$
lies in the image of
![]() ${\mathfrak {Z}}_n.$
${\mathfrak {Z}}_n.$
Note that
![]() $\mathbf {D}^{(n)}_{\mathrm {dR}}(M),$
for a
$\mathbf {D}^{(n)}_{\mathrm {dR}}(M),$
for a
![]() $(\varphi _L,\Gamma _L)$
-module
$(\varphi _L,\Gamma _L)$
-module
![]() $M,$
carries a natural filtration given by
$M,$
carries a natural filtration given by
Definition 5.11. Let M be a de Rham
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_K$
. We define the dual exponential map as the composite
$\mathcal {R}_K$
. We define the dual exponential map as the composite
Where the first map is given by mapping
![]() $[x,y]$
to
$[x,y]$
to
![]() $[\iota _\mu (y)]$
with
$[\iota _\mu (y)]$
with
![]() $\mu \gg 0.$
Its image is contained in
$\mu \gg 0.$
Its image is contained in
![]() $\operatorname {Fil}^0(D_{\mathrm {dR}}^{(n)}(M))$
and we thus obtain a map
$\operatorname {Fil}^0(D_{\mathrm {dR}}^{(n)}(M))$
and we thus obtain a map
We define
by taking
![]() $\Gamma _L$
-invariants of
$\Gamma _L$
-invariants of
![]() $\exp ^{*,(n)}_{\tilde {M}}$
, which is independent of the choice of
$\exp ^{*,(n)}_{\tilde {M}}$
, which is independent of the choice of
![]() $n.$
Indeed, as shown in [Reference Steingart50, Lem. 3.2.7] the restriction map
$n.$
Indeed, as shown in [Reference Steingart50, Lem. 3.2.7] the restriction map
for
![]() $m\geq n$
induces an isomorphism after taking
$m\geq n$
induces an isomorphism after taking
![]() $\Gamma _L$
-invariants, where
$\Gamma _L$
-invariants, where
![]() $\mathfrak {Q}_{m-n}({{\mathfrak {Z}}_n}):=\frac {{{\mathfrak {Z}}_m}}{{{\mathfrak {Z}}_n}}=\frac {\varphi _L^{m-n}({{\mathfrak {Z}}_n})}{{{\mathfrak {Z}}_n}}$
with
$\mathfrak {Q}_{m-n}({{\mathfrak {Z}}_n}):=\frac {{{\mathfrak {Z}}_m}}{{{\mathfrak {Z}}_n}}=\frac {\varphi _L^{m-n}({{\mathfrak {Z}}_n})}{{{\mathfrak {Z}}_n}}$
with
![]() $\mathfrak {Q}_{m-n}(0)=\pi _L^{m-n}$
and we have
$\mathfrak {Q}_{m-n}(0)=\pi _L^{m-n}$
and we have
![]() $C_g({{\mathfrak {Z}}_m})= \pi _L^{m-n}C_g({{\mathfrak {Z}}_n})$
by (48).
$C_g({{\mathfrak {Z}}_m})= \pi _L^{m-n}C_g({{\mathfrak {Z}}_n})$
by (48).
Definition 5.12. We define a pairing
given by
![]() $(x,y)\mapsto [x \otimes y].$
Furthermore we define
$(x,y)\mapsto [x \otimes y].$
Furthermore we define
as composite of
![]() $\cup _{\operatorname {\mathrm {dif}}}$
with
$\cup _{\operatorname {\mathrm {dif}}}$
with
using that
![]() $\mathbf {D}_{\mathrm {dR}}^{(n)}(\Omega ^1) \cong K_n$
via
$\mathbf {D}_{\mathrm {dR}}^{(n)}(\Omega ^1) \cong K_n$
via
![]() $t_{LT}^{-1}e \mapsto 1,$
where e corresponds to
$t_{LT}^{-1}e \mapsto 1,$
where e corresponds to
![]() $1$
in
$1$
in
![]() $\Omega ^1\cong \mathcal {R}_K(\delta )$
. We further define
$\Omega ^1\cong \mathcal {R}_K(\delta )$
. We further define
![]() $\langle -,- \rangle _{\mathrm {dR}}$
via the composite
$\langle -,- \rangle _{\mathrm {dR}}$
via the composite
Remark 5.13. The pairing
![]() $\langle -,- \rangle _{\mathrm {dR}}:=\langle -,- \rangle _{\mathrm {dR},M}$
$\langle -,- \rangle _{\mathrm {dR}}:=\langle -,- \rangle _{\mathrm {dR},M}$
is perfect if M is de Rham and induces a perfect pairing
Proof. Let us abbreviate
![]() $V:= \mathbf {D}_{\mathrm {dR}}^{(n)}(M), G = \Gamma _n$
and
$V:= \mathbf {D}_{\mathrm {dR}}^{(n)}(M), G = \Gamma _n$
and
![]() $B = K_n((t_{LT})).$
For a suitable
$B = K_n((t_{LT})).$
For a suitable
![]() $r_n$
we have that
$r_n$
we have that
![]() $V = (B\otimes _{\iota _n}M^{(n)})^G = (B\otimes _{K_n}V)^G$
by definition. We will first show that the pairing on the level of
$V = (B\otimes _{\iota _n}M^{(n)})^G = (B\otimes _{K_n}V)^G$
by definition. We will first show that the pairing on the level of
![]() $K_n$
is perfect. Observe that base change to B provides us with an injection
$K_n$
is perfect. Observe that base change to B provides us with an injection
![]() $\operatorname {Hom}_{K_n}(V,K_n) \hookrightarrow \operatorname {Hom}_B(B\otimes _{K_n} V,B).$
The target can be endowed with a G action by
$\operatorname {Hom}_{K_n}(V,K_n) \hookrightarrow \operatorname {Hom}_B(B\otimes _{K_n} V,B).$
The target can be endowed with a G action by
![]() $(g\lambda )(x) = g\lambda (g^{-1}x)$
and, because the action on V is trivial, we see that the image of the above map is precisely the set of G-invariant elements. Indeed, since
$(g\lambda )(x) = g\lambda (g^{-1}x)$
and, because the action on V is trivial, we see that the image of the above map is precisely the set of G-invariant elements. Indeed, since
![]() $B^G = K_n$
, a linear form
$B^G = K_n$
, a linear form
![]() $\lambda $
which is fixed by g has to map elements of the form
$\lambda $
which is fixed by g has to map elements of the form
![]() $1 \otimes v$
into
$1 \otimes v$
into
![]() $B^G = K_n$
and hence restricts to an element of
$B^G = K_n$
and hence restricts to an element of
![]() $\operatorname {Hom}_{K_n}(V,K_n).$
The perfectness now follows from
$\operatorname {Hom}_{K_n}(V,K_n).$
The perfectness now follows from
![]() $\operatorname {Hom}_B(B \otimes _{K_n} V,B) = \operatorname {Hom}_B(B \otimes _{\iota _n} M,B) \cong \operatorname {Hom}_B(B \otimes _{\iota _n} M,B(\chi _{LT}))\cong B \otimes _{\iota _n}\tilde {M}$
by taking G-invariants, using that the evaluation pairing commutes with base change. Note that we used that
$\operatorname {Hom}_B(B \otimes _{K_n} V,B) = \operatorname {Hom}_B(B \otimes _{\iota _n} M,B) \cong \operatorname {Hom}_B(B \otimes _{\iota _n} M,B(\chi _{LT}))\cong B \otimes _{\iota _n}\tilde {M}$
by taking G-invariants, using that the evaluation pairing commutes with base change. Note that we used that
![]() $B = B(\chi _{LT})$
as
$B = B(\chi _{LT})$
as
![]() $\Gamma _L$
-modules (since
$\Gamma _L$
-modules (since
![]() $B^\times $
contains
$B^\times $
contains
![]() $t_{LT}$
) and that
$t_{LT}$
) and that
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}}}(M(\chi _{LT})) \cong \mathbf {D}_{\operatorname {\mathrm {dif}}}(M(\chi ))$
as they have “the same”
$\mathbf {D}_{\operatorname {\mathrm {dif}}}(M(\chi _{LT})) \cong \mathbf {D}_{\operatorname {\mathrm {dif}}}(M(\chi ))$
as they have “the same”
![]() $\Gamma _L$
-action. To conclude perfectness of the K-valued pairing, it suffices to show that the pairing is non-degenerate on one side. Set
$\Gamma _L$
-action. To conclude perfectness of the K-valued pairing, it suffices to show that the pairing is non-degenerate on one side. Set
![]() $W = \operatorname {Hom}_{K_n}(V,K_n).$
Let
$W = \operatorname {Hom}_{K_n}(V,K_n).$
Let
![]() $V':=\operatorname {Hom}_K(V,K)$
which we view as a
$V':=\operatorname {Hom}_K(V,K)$
which we view as a
![]() $K_n$
-module in the obvious way; we endow W and
$K_n$
-module in the obvious way; we endow W and
![]() $V'$
with a
$V'$
with a
![]() $\Gamma _L/\Gamma _n$
-action via
$\Gamma _L/\Gamma _n$
-action via
![]() $\gamma f(-)=\gamma f(\gamma ^{-1}-)$
. By the above perfectness at the level of
$\gamma f(-)=\gamma f(\gamma ^{-1}-)$
. By the above perfectness at the level of
![]() $K_n$
it thus suffices to show that the map
$K_n$
it thus suffices to show that the map
![]() $W \to V'$
given by
$W \to V'$
given by
![]() $w \mapsto \operatorname {Tr}_{K_n/K}(w(-))$
is injective. One easily checks that it is compatible with the
$w \mapsto \operatorname {Tr}_{K_n/K}(w(-))$
is injective. One easily checks that it is compatible with the
![]() $K_n$
- and
$K_n$
- and
![]() $\Gamma _L/\Gamma _n$
-structure on
$\Gamma _L/\Gamma _n$
-structure on
![]() $V'.$
We thus have constructed a
$V'.$
We thus have constructed a
![]() $\Gamma _L/\Gamma _n$
-semilinear map between free
$\Gamma _L/\Gamma _n$
-semilinear map between free
![]() $K_n$
-modules of the same rank. By Galois descent it suffices to show that it is injective on
$K_n$
-modules of the same rank. By Galois descent it suffices to show that it is injective on
![]() $\Gamma _L/\Gamma _n$
-invariant elements. Suppose
$\Gamma _L/\Gamma _n$
-invariant elements. Suppose
![]() $w \in W^{\Gamma _L}$
satisfies
$w \in W^{\Gamma _L}$
satisfies
![]() $\operatorname {Tr}_{K_n/K}(w(v))=0$
for all
$\operatorname {Tr}_{K_n/K}(w(v))=0$
for all
![]() $v \in V.$
This means that the image of the map
$v \in V.$
This means that the image of the map
![]() $w\colon V \to K_n$
is contained in the kernel of the trace map. For any
$w\colon V \to K_n$
is contained in the kernel of the trace map. For any
![]() $x\in V^{\Gamma _L}$
, we obtain
$x\in V^{\Gamma _L}$
, we obtain
![]() $w(x) \in K \cap \operatorname {ker}(Tr)=0$
by the
$w(x) \in K \cap \operatorname {ker}(Tr)=0$
by the
![]() $\Gamma _L $
-equivariance of w. Thus w is trivial on
$\Gamma _L $
-equivariance of w. Thus w is trivial on
![]() $\Gamma _L$
-invariants and by Galois descent trivial, because V is generated by
$\Gamma _L$
-invariants and by Galois descent trivial, because V is generated by
![]() $\Gamma _L$
-invariant elements, which implies
$\Gamma _L$
-invariant elements, which implies
![]() $w=0.$
$w=0.$
For the second statement observe first that
![]() $\operatorname {Fil}^0(\mathbf {D}^{(n)}_{dR}(\Omega ^1))=0$
and
$\operatorname {Fil}^0(\mathbf {D}^{(n)}_{dR}(\Omega ^1))=0$
and
![]() $\operatorname {Fil}^{-1}(\mathbf {D}_{dR}^{(n)}(\Omega ^1)))=K_n.$
Hence
$\operatorname {Fil}^{-1}(\mathbf {D}_{dR}^{(n)}(\Omega ^1)))=K_n.$
Hence
![]() $\operatorname {Fil}^{0}(\mathbf {D}^{(n)}_{dR}(M))$
is contained in the subspace orthogonal to
$\operatorname {Fil}^{0}(\mathbf {D}^{(n)}_{dR}(M))$
is contained in the subspace orthogonal to
![]() $\operatorname {Fil}^0\mathbf {D}_{dR}^{(n)}(\tilde {M})$
. In order to see that this inclusion is an equality, it suffices to show that the canonical bijective morphism of filtered vectorspaces
$\operatorname {Fil}^0\mathbf {D}_{dR}^{(n)}(\tilde {M})$
. In order to see that this inclusion is an equality, it suffices to show that the canonical bijective morphism of filtered vectorspaces
![]() $\mathbf {D}^{(n)}_{\mathrm {dR}}(M) \otimes \mathbf {D}^{(n)}_{\mathrm {dR}}(\tilde {M}) \cong \mathbf {D}_{\mathrm {dR}}^{(n)}(M\otimes \tilde {M})$
is in fact an isomorphism. This is not entirely trivial and can be achieved by an analogue of [Reference Brinon and Conrad9, Proposition 6.3.3]. As in their case one reduces to the corresponding statement about graded objects and finally to the corresponding statement of rank one objects (which is clear in our case as well).
$\mathbf {D}^{(n)}_{\mathrm {dR}}(M) \otimes \mathbf {D}^{(n)}_{\mathrm {dR}}(\tilde {M}) \cong \mathbf {D}_{\mathrm {dR}}^{(n)}(M\otimes \tilde {M})$
is in fact an isomorphism. This is not entirely trivial and can be achieved by an analogue of [Reference Brinon and Conrad9, Proposition 6.3.3]. As in their case one reduces to the corresponding statement about graded objects and finally to the corresponding statement of rank one objects (which is clear in our case as well).
Lemma 5.14. The diagram

is commutative.
Proof. Given any
![]() $a\in K_n$
(in the right upper corner of the diagram) we first have to calculate
$a\in K_n$
(in the right upper corner of the diagram) we first have to calculate
![]() $\delta _2(1\otimes \frac {a}{t_{LT}}\mathbf {e}_\chi )$
as
$\delta _2(1\otimes \frac {a}{t_{LT}}\mathbf {e}_\chi )$
as
![]() $x:=1\otimes \frac {a}{t_{LT}}\mathbf {e}_\chi \in K_n[[t_{LT}]][\frac {1}{t_{LT}}]\mathbf {e}_\chi =\mathbf {D}_{\operatorname {\mathrm {dif}},n}(\Omega ^1)$
represents - up to a constant - the image of
$x:=1\otimes \frac {a}{t_{LT}}\mathbf {e}_\chi \in K_n[[t_{LT}]][\frac {1}{t_{LT}}]\mathbf {e}_\chi =\mathbf {D}_{\operatorname {\mathrm {dif}},n}(\Omega ^1)$
represents - up to a constant - the image of
![]() $\frac {a}{t_{LT}}\mathbf {e}_\chi \in D_{\mathrm {dR}}^{(n)}(\Omega ^1) $
under
$\frac {a}{t_{LT}}\mathbf {e}_\chi \in D_{\mathrm {dR}}^{(n)}(\Omega ^1) $
under
![]() $g^{(n)}_{\Omega ^1}.$
In order to calculate the transition map
$g^{(n)}_{\Omega ^1}.$
In order to calculate the transition map
![]() $\delta _2$
we use an analogue of [Reference Nakamura35, Lem. 2.12(2)], which is an easy snake-lemma application to 5.7: Assume that x belongs to
$\delta _2$
we use an analogue of [Reference Nakamura35, Lem. 2.12(2)], which is an easy snake-lemma application to 5.7: Assume that x belongs to
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}},k}(\Omega ^1)$
for some
$\mathbf {D}_{\operatorname {\mathrm {dif}},k}(\Omega ^1)$
for some
![]() $ k\geq 0.$
For any element
$ k\geq 0.$
For any element
![]() $\tilde {x}\in \frac {1}{t_{LT}}\Omega ^{1,(k)}=\frac {1}{t_{LT}}\mathcal {R}(\chi )^{(k)}$
such that
$\tilde {x}\in \frac {1}{t_{LT}}\Omega ^{1,(k)}=\frac {1}{t_{LT}}\mathcal {R}(\chi )^{(k)}$
such that
(using the notation of Definition 3.15) for all
![]() $m\geq k,$
we then have
$m\geq k,$
we then have
![]() $\delta _2([x])=[(\varphi -1)\tilde {x}]\in H^2_{\varphi ,{\mathfrak {Z}}_n}(\Omega ^1).$
$\delta _2([x])=[(\varphi -1)\tilde {x}]\in H^2_{\varphi ,{\mathfrak {Z}}_n}(\Omega ^1).$
We construct
![]() $\tilde {x}$
as follows. Consider the isomorphism
$\tilde {x}$
as follows. Consider the isomorphism
analogous to (42) and let f be an element in
![]() $ \mathcal {R}_F^{+}$
, whose class in the left hand side corresponds to the tuple
$ \mathcal {R}_F^{+}$
, whose class in the left hand side corresponds to the tuple
![]() $(a_\mu )_{\mu \geq 0}$
with
$(a_\mu )_{\mu \geq 0}$
with
 $$\begin{align*}a_\mu:=\left\{ \begin{array}{ll} \frac{a}{q^{\mu-k}\pi_L^k}, & \text{if } \mu\geq k; \\ \frac{\mathrm{Tr}_{K_k/K_\mu}(a)}{\pi_L^k}, & \text{if } k\geq\mu\geq 0; \end{array} \right. \end{align*}$$
$$\begin{align*}a_\mu:=\left\{ \begin{array}{ll} \frac{a}{q^{\mu-k}\pi_L^k}, & \text{if } \mu\geq k; \\ \frac{\mathrm{Tr}_{K_k/K_\mu}(a)}{\pi_L^k}, & \text{if } k\geq\mu\geq 0; \end{array} \right. \end{align*}$$
on the right hand side. Note that the operator
![]() $\Psi $
on
$\Psi $
on
![]() $\mathcal {R}^+_K$
induces the map
$\mathcal {R}^+_K$
induces the map
 $$ \begin{align*} \Psi:\prod_{\mu\geq 0} K_\mu &\to \prod_{\mu\geq 0} K_\mu, \\ (x_\mu)&\mapsto (q^{-1}x_0+q^{-1}\mathrm{Tr}_{K_1/K_0}(x_1),q^{-1}\mathrm{Tr}_{K_2/K_1}(x_2),\ldots, q^{-1}\mathrm{Tr}_{K_{\mu+1}/K_\mu}(x_{\mu+1}),\ldots ). \end{align*} $$
$$ \begin{align*} \Psi:\prod_{\mu\geq 0} K_\mu &\to \prod_{\mu\geq 0} K_\mu, \\ (x_\mu)&\mapsto (q^{-1}x_0+q^{-1}\mathrm{Tr}_{K_1/K_0}(x_1),q^{-1}\mathrm{Tr}_{K_2/K_1}(x_2),\ldots, q^{-1}\mathrm{Tr}_{K_{\mu+1}/K_\mu}(x_{\mu+1}),\ldots ). \end{align*} $$
Moreover,
![]() $(x_\mu )_\mu $
satisfies
$(x_\mu )_\mu $
satisfies
![]() $q\Psi ((x_\mu )_\mu )= (x_\mu )_\mu $
if and only
$q\Psi ((x_\mu )_\mu )= (x_\mu )_\mu $
if and only
![]() $\mathrm {Tr}_{K_1/K_0}(x_1)=0$
and
$\mathrm {Tr}_{K_1/K_0}(x_1)=0$
and
![]() $\mathrm {Tr}_{K_{m+1}/K_{m}}(x_{m+1})=x_{m}$
for all
$\mathrm {Tr}_{K_{m+1}/K_{m}}(x_{m+1})=x_{m}$
for all
![]() $m\geq 1.$
In particular,
$m\geq 1.$
In particular,
![]() $q\Psi ((a_\mu )_\mu )= (a_\mu )_\mu $
if and only if
$q\Psi ((a_\mu )_\mu )= (a_\mu )_\mu $
if and only if
![]() $ \mathrm {Tr}_{K_{k}/K_{0}}(a)=0.$
We now set
$ \mathrm {Tr}_{K_{k}/K_{0}}(a)=0.$
We now set
![]() $\tilde {x}=\frac {f}{t_{LT}}\mathbf {e}_\chi \in \frac {1}{t_{LT}}\mathcal {R}(\chi )^{(k)}$
and check that, for
$\tilde {x}=\frac {f}{t_{LT}}\mathbf {e}_\chi \in \frac {1}{t_{LT}}\mathcal {R}(\chi )^{(k)}$
and check that, for
![]() $m\geq k$
,
$m\geq k$
,
 $$ \begin{align*} \iota_m(\tilde{x}) & \equiv \frac{\pi_L^mf(u_m)}{t_{LT}}\mathbf{e}_\chi \; \mod \mathbf{D}_{\operatorname{\mathrm{dif}},m}^+(\mathcal{R}(\chi)) \\ & = \frac{\pi_L^m a_m}{t_{LT}}\mathbf{e}_\chi\\ & = \frac{\pi_L^{m-k} a }{q^{m-k}t_{LT}}\mathbf{e}_\chi\\ & = \mathrm{can}_{k,m}(x) \end{align*} $$
$$ \begin{align*} \iota_m(\tilde{x}) & \equiv \frac{\pi_L^mf(u_m)}{t_{LT}}\mathbf{e}_\chi \; \mod \mathbf{D}_{\operatorname{\mathrm{dif}},m}^+(\mathcal{R}(\chi)) \\ & = \frac{\pi_L^m a_m}{t_{LT}}\mathbf{e}_\chi\\ & = \frac{\pi_L^{m-k} a }{q^{m-k}t_{LT}}\mathbf{e}_\chi\\ & = \mathrm{can}_{k,m}(x) \end{align*} $$
as required, i.e.,
![]() $\delta _2(1\otimes \frac {a}{t_{LT}}\mathbf {e}_\chi )=[(\varphi -1)(\frac {f}{t_{LT}}\mathbf {e}_\chi )]=[\left (\frac {\varphi (f)}{q}-f\right )\frac {1}{t_{LT}}\mathbf {e}_\chi ]$
. Since
$\delta _2(1\otimes \frac {a}{t_{LT}}\mathbf {e}_\chi )=[(\varphi -1)(\frac {f}{t_{LT}}\mathbf {e}_\chi )]=[\left (\frac {\varphi (f)}{q}-f\right )\frac {1}{t_{LT}}\mathbf {e}_\chi ]$
. Since
 $$ \begin{align*} \left(\frac{\varphi(f)}{q}-f\right)(u_m)= & \frac{ f(u_{m-1})}{q}-f(u_m)= \frac{ a_{m-1} }{q}-a_m=0 \end{align*} $$
$$ \begin{align*} \left(\frac{\varphi(f)}{q}-f\right)(u_m)= & \frac{ f(u_{m-1})}{q}-f(u_m)= \frac{ a_{m-1} }{q}-a_m=0 \end{align*} $$
for all
![]() $m>k$
, we conclude from (53) that
$m>k$
, we conclude from (53) that
![]() $\frac {\varphi (f)}{q}-f\in \left (\prod _{m>k}^{\infty }\frac {Q_m}{\pi _L} \right )\mathcal {R}^+_K, $
whence
$\frac {\varphi (f)}{q}-f\in \left (\prod _{m>k}^{\infty }\frac {Q_m}{\pi _L} \right )\mathcal {R}^+_K, $
whence
 $$ \begin{align} \left(\frac{\varphi(f)}{q}-f\right)\frac{1}{t_{LT}}\in \frac{\left(\prod_{m>k}^{\infty}\frac{Q_m}{\pi_L} \right)}{t_{LT}}\mathcal{R}^+_K=\frac{1}{Z\prod_{\mu\geq 1}^k\frac{Q_\mu} {\pi_L}}\mathcal{R}^+_K \end{align} $$
$$ \begin{align} \left(\frac{\varphi(f)}{q}-f\right)\frac{1}{t_{LT}}\in \frac{\left(\prod_{m>k}^{\infty}\frac{Q_m}{\pi_L} \right)}{t_{LT}}\mathcal{R}^+_K=\frac{1}{Z\prod_{\mu\geq 1}^k\frac{Q_\mu} {\pi_L}}\mathcal{R}^+_K \end{align} $$
using
![]() $t_{LT}=Z\prod _{\mu \geq 1}\frac {Q_\mu } {\pi _L}.$
Since all involved maps are K-linear and
$t_{LT}=Z\prod _{\mu \geq 1}\frac {Q_\mu } {\pi _L}.$
Since all involved maps are K-linear and
![]() $K_n=K\oplus \ker (\mathrm {Tr}_{K_n/K})$
it suffices to check the commutativity in the two cases
$K_n=K\oplus \ker (\mathrm {Tr}_{K_n/K})$
it suffices to check the commutativity in the two cases
![]() $a\in K,$
i.e.,
$a\in K,$
i.e.,
![]() $k=0$
, or
$k=0$
, or
![]() $\mathrm {Tr}_{K_n/K}(a)=0,$
i.e.,
$\mathrm {Tr}_{K_n/K}(a)=0,$
i.e.,
![]() $q\Psi ((a_\mu )_{\mu \geq 0}) = (a_\mu )_{\mu \geq 0}.$
$q\Psi ((a_\mu )_{\mu \geq 0}) = (a_\mu )_{\mu \geq 0}.$
If
![]() $k=0$
, the element
$k=0$
, the element
![]() $\frac {a}{t_{LT}}\mathbf {e}_\chi $
is sent via the lower composite to
$\frac {a}{t_{LT}}\mathbf {e}_\chi $
is sent via the lower composite to
 $$ \begin{align*} C_{Tr}({{\mathfrak{Z}}_n})Res\circ (-\delta_2)\circ g_{\Omega^1}(\frac{a}{t_{LT}}\mathbf{e}_\chi ) & =-C_g({{\mathfrak{Z}}_n}) C_{Tr}({{\mathfrak{Z}}_n})Res\circ \delta_2(1\otimes \frac{a}{t_{LT}}\mathbf{e}_\chi) \\ & =-\frac{q}{q-1} Res (\left(\frac{\varphi(f)}{q}-f\right)\frac{1}{t_{LT}}dt_{LT}) \\ & =-\frac{q}{q-1} \left(\frac{\varphi(f)}{q}-f\right)_{|Z=0}\\ & =-\frac{q}{q-1} \left(\frac{f(0)}{q}-f(0) \right) =a \end{align*} $$
$$ \begin{align*} C_{Tr}({{\mathfrak{Z}}_n})Res\circ (-\delta_2)\circ g_{\Omega^1}(\frac{a}{t_{LT}}\mathbf{e}_\chi ) & =-C_g({{\mathfrak{Z}}_n}) C_{Tr}({{\mathfrak{Z}}_n})Res\circ \delta_2(1\otimes \frac{a}{t_{LT}}\mathbf{e}_\chi) \\ & =-\frac{q}{q-1} Res (\left(\frac{\varphi(f)}{q}-f\right)\frac{1}{t_{LT}}dt_{LT}) \\ & =-\frac{q}{q-1} \left(\frac{\varphi(f)}{q}-f\right)_{|Z=0}\\ & =-\frac{q}{q-1} \left(\frac{f(0)}{q}-f(0) \right) =a \end{align*} $$
where we use for the second equality the definition (20) and for the third equality (54). Thus the claim follows on the subspace
![]() $D_{\mathrm {dR}}^{(n)}(\Omega ^1)^{\Gamma _L}, $
because
$D_{\mathrm {dR}}^{(n)}(\Omega ^1)^{\Gamma _L}, $
because
![]() $ \frac {1}{[K_n:K]}Tr_{K_n/K}(a) =a$
.
$ \frac {1}{[K_n:K]}Tr_{K_n/K}(a) =a$
.
If
![]() $q\Psi ((a_\mu )_{\mu \geq 0}) = (a_\mu )_{\mu \geq 0}$
, i.e.,
$q\Psi ((a_\mu )_{\mu \geq 0}) = (a_\mu )_{\mu \geq 0}$
, i.e.,
![]() $q\Psi (f\mod t_{LT}) \equiv f\mod t_{LT}$
, it follows from the surjectivity of
$q\Psi (f\mod t_{LT}) \equiv f\mod t_{LT}$
, it follows from the surjectivity of
![]() $\frac {1}{\pi _L}\Psi -\frac {1}{q}$
on
$\frac {1}{\pi _L}\Psi -\frac {1}{q}$
on
![]() $\mathcal {R}^+$
by [Reference Berger and Fourquaux6, Cor. 2.3.4] and the commutative diagram with exact rows
$\mathcal {R}^+$
by [Reference Berger and Fourquaux6, Cor. 2.3.4] and the commutative diagram with exact rows

that we may assume without loss of generality that f also satisfies
![]() $q\Psi (f)=f,$
whence we obtain
$q\Psi (f)=f,$
whence we obtain
![]() $\Psi (\frac {\varphi (f)}{q}-f)=0.$
Using the identity
$\Psi (\frac {\varphi (f)}{q}-f)=0.$
Using the identity
![]() $Res(\Psi (f)dt_{LT})=\chi (\pi _L)Res(fdt_{LT})$
from [Reference Colmez15, Prop. 1.5] we conclude that
$Res(\Psi (f)dt_{LT})=\chi (\pi _L)Res(fdt_{LT})$
from [Reference Colmez15, Prop. 1.5] we conclude that
![]() $Res (\left (\frac {\varphi (f)}{q}-f\right )\frac {1}{t_{LT}}dt_{LT})$
vanishes, from which the commutativity follows also in this case by a similar calculation as above.
$Res (\left (\frac {\varphi (f)}{q}-f\right )\frac {1}{t_{LT}}dt_{LT})$
vanishes, from which the commutativity follows also in this case by a similar calculation as above.
Lemma 5.15. Let
![]() $z \in H^0_{{\mathfrak {Z}}_n}(\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)),[x,y] \in H^1_{\varphi , {\mathfrak {Z}}_n}(\tilde {M}), a \in H^0_{\varphi ,{\mathfrak {Z}}_n}(M)$
and
$z \in H^0_{{\mathfrak {Z}}_n}(\mathbf {D}_{\operatorname {\mathrm {dif}}}(M)),[x,y] \in H^1_{\varphi , {\mathfrak {Z}}_n}(\tilde {M}), a \in H^0_{\varphi ,{\mathfrak {Z}}_n}(M)$
and
![]() $[b] \in H^2_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M}).$
Using
$[b] \in H^2_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M}).$
Using
![]() $\langle -,-\rangle :=\langle -,-\rangle _M$
as before to denote the pairing
$\langle -,-\rangle :=\langle -,-\rangle _M$
as before to denote the pairing
obtained from 4.16 we have
and
Proof. Let z be in
![]() $\mathbf {D}_{\mathrm {dR}}^{(n)}(M)$
and
$\mathbf {D}_{\mathrm {dR}}^{(n)}(M)$
and
![]() $[x,y]\in H^1_{\varphi , {\mathfrak {Z}}_n}(\tilde {M})$
with
$[x,y]\in H^1_{\varphi , {\mathfrak {Z}}_n}(\tilde {M})$
with
![]() $x\in \tilde {M}^{(n)}, y\in \tilde {M}^{(n+1)}.$
Then we have
$x\in \tilde {M}^{(n)}, y\in \tilde {M}^{(n+1)}.$
Then we have
by (52) and, by the same snake-lemma application in order to calculate the transition map
![]() $\delta _2$
induced by Proposition 5.7 (compare with [Reference Nakamura35, Lem. 2.12(2)]),
$\delta _2$
induced by Proposition 5.7 (compare with [Reference Nakamura35, Lem. 2.12(2)]),
 $$ \begin{align*} -Tr\Big( \delta_2([z\otimes \iota_n(y)])\Big) & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big([(\varphi-1)(\tilde{z}\otimes y)]\Big) \\ & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big([(\varphi-1)(\tilde{z})\otimes\varphi( y)+\tilde{z}\otimes {{\mathfrak{Z}}}_n x]\Big)\\ & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big( \varphi(y)\big((\varphi-1)(\tilde{z})\big)+ \big({{\mathfrak{Z}}}_n x \big)(\tilde{z}) \Big), \end{align*} $$
$$ \begin{align*} -Tr\Big( \delta_2([z\otimes \iota_n(y)])\Big) & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big([(\varphi-1)(\tilde{z}\otimes y)]\Big) \\ & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big([(\varphi-1)(\tilde{z})\otimes\varphi( y)+\tilde{z}\otimes {{\mathfrak{Z}}}_n x]\Big)\\ & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big( \varphi(y)\big((\varphi-1)(\tilde{z})\big)+ \big({{\mathfrak{Z}}}_n x \big)(\tilde{z}) \Big), \end{align*} $$
where in the second equality we have used the co-boundary condition
![]() $(\varphi -1)(y)={{\mathfrak {Z}}}_nx.$
Moreover,
$(\varphi -1)(y)={{\mathfrak {Z}}}_nx.$
Moreover,
![]() $\tilde {z}\in M^{(n)}_{t_{LT}}$
is an element with the property that
$\tilde {z}\in M^{(n)}_{t_{LT}}$
is an element with the property that
![]() $\iota _m(\tilde {z})-z$
belongs to
$\iota _m(\tilde {z})-z$
belongs to
![]() $\mathbf {D}_{\operatorname {\mathrm {dif}},m}^+(M)$
for all
$\mathbf {D}_{\operatorname {\mathrm {dif}},m}^+(M)$
for all
![]() $m\geq n$
, the existence of which is granted by the exactness of (40), whence
$m\geq n$
, the existence of which is granted by the exactness of (40), whence
![]() $\iota _m(\tilde {z}\otimes y)-z\otimes \iota _m(y)\in \mathbf {D}_{\operatorname {\mathrm {dif}},m}^+(M\otimes \tilde {M})$
for all
$\iota _m(\tilde {z}\otimes y)-z\otimes \iota _m(y)\in \mathbf {D}_{\operatorname {\mathrm {dif}},m}^+(M\otimes \tilde {M})$
for all
![]() $m\geq n$
.
$m\geq n$
.
On the other hand we have by a straightforward analogue of [Reference Nakamura35, Lem. 2.12 (1)] for the first, the formula in Theorem 4.16 for the second equality and (22) for the third equality
 $$ \begin{align*} \langle\exp_M^{(n)}(z), [x,y]\rangle & =\langle [(\varphi-1)(\tilde{z}), {{\mathfrak{Z}}}_n\tilde{z} ],[x,y]\rangle\\ & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big( \varphi(y)\big((\varphi-1)(\tilde{z})\big)+(\lambda^\iota x)({{\mathfrak{Z}}}_n\tilde{z}) \Big) \\ &=-C_{Tr}({{\mathfrak{Z}}_n})Res\Big( \varphi(y)\big((\varphi-1)(\tilde{z})\big)+ \big({{\mathfrak{Z}}}_n x \big)(\tilde{z}) \Big), \end{align*} $$
$$ \begin{align*} \langle\exp_M^{(n)}(z), [x,y]\rangle & =\langle [(\varphi-1)(\tilde{z}), {{\mathfrak{Z}}}_n\tilde{z} ],[x,y]\rangle\\ & =-C_{Tr}({{\mathfrak{Z}}_n})Res\Big( \varphi(y)\big((\varphi-1)(\tilde{z})\big)+(\lambda^\iota x)({{\mathfrak{Z}}}_n\tilde{z}) \Big) \\ &=-C_{Tr}({{\mathfrak{Z}}_n})Res\Big( \varphi(y)\big((\varphi-1)(\tilde{z})\big)+ \big({{\mathfrak{Z}}}_n x \big)(\tilde{z}) \Big), \end{align*} $$
which agrees with the above formula. We leave the easy proof of the second identity to the reader.
Proposition 5.16. Let M be de Rham. Let
![]() $x \in \mathbf {D}_{\mathrm {dR}}^{(n)}(M)/\operatorname {Fil}^0\mathbf {D}_{\mathrm {dR}}^{(n)}(M)$
and
$x \in \mathbf {D}_{\mathrm {dR}}^{(n)}(M)/\operatorname {Fil}^0\mathbf {D}_{\mathrm {dR}}^{(n)}(M)$
and
![]() $y \in H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M}).$
We have
$y \in H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M}).$
We have
i.e.,
![]() $\exp ^{(n)}_{M}$
is adjoint to
$\exp ^{(n)}_{M}$
is adjoint to
![]() $ \exp _{M}^{*,(n)}.$
$ \exp _{M}^{*,(n)}.$
Proof. This is a formal consequence of Lemma 5.15 after plugging in the definition 5.11 of
![]() $\exp _{M}^{*,(n)}.$
$\exp _{M}^{*,(n)}.$
Only for the purpose of the next lemma (needed in the proof of the subsequent proposition) we introduce the notation
![]() $H^i_{\mathrm {mix}}(N)$
as the i-th cohomology of the complex
$H^i_{\mathrm {mix}}(N)$
as the i-th cohomology of the complex
![]() $ K_{{\mathfrak {Z}}_n}^{(\varphi )}(N_{t_{LT}}) \oplus K_{{\mathfrak {Z}}_n}(\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(N)) $
of the bottom right in Proposition 5.7. We define a pairing
$ K_{{\mathfrak {Z}}_n}^{(\varphi )}(N_{t_{LT}}) \oplus K_{{\mathfrak {Z}}_n}(\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(N)) $
of the bottom right in Proposition 5.7. We define a pairing
given by
![]() $(x,y)\mapsto [x \otimes y].$
Furthermore, we set
$(x,y)\mapsto [x \otimes y].$
Furthermore, we set
Finally, by
we denote the composite
![]() $H^1(d_7)\circ H^1(d_3),$
where
$H^1(d_7)\circ H^1(d_3),$
where
![]() $d_7:K_{{\mathfrak {Z}}_n}^{(\varphi )}(\tilde {M}_{t_{LT}})\oplus K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif}}^+(\tilde {M})) \to K_{{\mathfrak {Z}}_n}^{(\varphi )}(\tilde {M}_{t_{LT}}) \oplus K_{{\mathfrak {Z}}_n}(\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(\tilde {M}))$
sends
$d_7:K_{{\mathfrak {Z}}_n}^{(\varphi )}(\tilde {M}_{t_{LT}})\oplus K_{{\mathfrak {Z}}_n}(\mathbf {D}_{\mathrm {dif}}^+(\tilde {M})) \to K_{{\mathfrak {Z}}_n}^{(\varphi )}(\tilde {M}_{t_{LT}}) \oplus K_{{\mathfrak {Z}}_n}(\operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(\tilde {M}))$
sends
![]() $(x,y)$
to itself using the natural inclusion
$(x,y)$
to itself using the natural inclusion
![]() $ \mathbf {D}_{\mathrm {dif}}^+(\tilde {M}) \hookrightarrow \operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(\tilde {M})$
. Then the next Lemma is formally analogous to Lemma 5.15, thus we leave the details to the interested reader.
$ \mathbf {D}_{\mathrm {dif}}^+(\tilde {M}) \hookrightarrow \operatorname {{{\mathbf {D}}_{\mathrm {dif}}}}(\tilde {M})$
. Then the next Lemma is formally analogous to Lemma 5.15, thus we leave the details to the interested reader.
Lemma 5.17. The following diagram is commutative

Proposition 5.18. Let
![]() $M $
be a trianguline L-analytic
$M $
be a trianguline L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_K$
which is de Rham. Then
$\mathcal {R}_K$
which is de Rham. Then
![]() $H^1_{\varphi ,{\mathfrak {Z}}_n}(M)^{\Gamma _L}_f$
is the orthogonal complement of
$H^1_{\varphi ,{\mathfrak {Z}}_n}(M)^{\Gamma _L}_f$
is the orthogonal complement of
![]() $H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M})^{\Gamma _L}_f$
with respect to the duality pairing
$H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M})^{\Gamma _L}_f$
with respect to the duality pairing
![]() $\langle -,- \rangle _M.$
$\langle -,- \rangle _M.$
Proof. Analogous to [Reference Nakamura36, Prop. 2.24]: Replacing the sequence (13) in (loc. cit.) by (46), using the Euler-Poincaré formula 4.7 as well as duality 4.16 and the de Rham property of M one shows that
![]() $\dim _KH^1_{\varphi ,{\mathfrak {Z}}_n}(M)^{\Gamma _L}_f+\dim _K H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M})^{\Gamma _L}_f=\dim _K H^1_{\varphi ,{\mathfrak {Z}}_n}({M})^{\Gamma _L}.$
Therefore it suffices to show that
$\dim _KH^1_{\varphi ,{\mathfrak {Z}}_n}(M)^{\Gamma _L}_f+\dim _K H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M})^{\Gamma _L}_f=\dim _K H^1_{\varphi ,{\mathfrak {Z}}_n}({M})^{\Gamma _L}.$
Therefore it suffices to show that
![]() $\langle x,y \rangle =0$
for all
$\langle x,y \rangle =0$
for all
![]() $x\in H^1_{\varphi ,{\mathfrak {Z}}_n}(M)^{\Gamma _L}_f $
and
$x\in H^1_{\varphi ,{\mathfrak {Z}}_n}(M)^{\Gamma _L}_f $
and
![]() $y\in H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M})^{\Gamma _L}_f .$
This is accomplished by Lemma 5.17, because
$y\in H^1_{\varphi ,{\mathfrak {Z}}_n}(\tilde {M})^{\Gamma _L}_f .$
This is accomplished by Lemma 5.17, because
![]() $G(y)=0$
since
$G(y)=0$
since
![]() $y\in \ker H^1(d_3)$
by assumption.
$y\in \ker H^1(d_3)$
by assumption.
6
 $\epsilon $
-constants
$\epsilon $
-constants
Let E be a field of characteristic zero containing
![]() $\mu _{p^\infty }$
,
$\mu _{p^\infty }$
,
![]() $\psi _0:=\psi _\xi : {\Bbb Q}_p\to E^\times $
the character (with kernel
$\psi _0:=\psi _\xi : {\Bbb Q}_p\to E^\times $
the character (with kernel
![]() $\mathbb {Z}_p$
) attached to a fixed compatible system
$\mathbb {Z}_p$
) attached to a fixed compatible system
![]() $\xi =(\xi _n)_{n\geq 1}$
of p-power roots of unity via
$\xi =(\xi _n)_{n\geq 1}$
of p-power roots of unity via
![]() $\psi _0(\frac {1}{p^n})=\xi _n$
.
$\psi _0(\frac {1}{p^n})=\xi _n$
.
Similarly, we may define for the compatible system
![]() $u=(u_n)_{n\in \mathbb {N}}\in T_\pi $
(and a choice of generator
$u=(u_n)_{n\in \mathbb {N}}\in T_\pi $
(and a choice of generator
![]() $t_0'$
of
$t_0'$
of
![]() $T_{\pi }'$
) the character
$T_{\pi }'$
) the character
![]() $\psi _u:=\psi _{u,t_0'}:L\to E^\times ,\; \frac {x}{\pi _L^n}\mapsto \eta _{t_0'}(x,u_n).$
$\psi _u:=\psi _{u,t_0'}:L\to E^\times ,\; \frac {x}{\pi _L^n}\mapsto \eta _{t_0'}(x,u_n).$
But there is another (canonical) choice:
![]() $\psi _L:=\psi _0\circ \mathrm {Tr}_{L/{\Bbb Q}_p}: L\to E^\times $
is a locally constant character (with kernel the inverse of the different ideal
$\psi _L:=\psi _0\circ \mathrm {Tr}_{L/{\Bbb Q}_p}: L\to E^\times $
is a locally constant character (with kernel the inverse of the different ideal
![]() $\mathfrak {D}_{L/{\Bbb Q}_p} $
).
$\mathfrak {D}_{L/{\Bbb Q}_p} $
).
Remark 6.1. The character
![]() $\psi _L$
factorizes over
$\psi _L$
factorizes over
![]() $o_L.$
Hence, by (4) there exists
$o_L.$
Hence, by (4) there exists
![]() $a=a(t_0',u)\in o_L$
such that the following diagram commutes
$a=a(t_0',u)\in o_L$
such that the following diagram commutes

Here
![]() $\eta _{t_0'}(1,u):=(\eta _{t_0'}(1,u_n))_n$
is a generator of
$\eta _{t_0'}(1,u):=(\eta _{t_0'}(1,u_n))_n$
is a generator of
![]() $\mathbb {Z}_p(1)$
, again by (4). In particular, for the choice
$\mathbb {Z}_p(1)$
, again by (4). In particular, for the choice
![]() $\xi =\eta _{t_0'}(1,u)$
we obtain
$\xi =\eta _{t_0'}(1,u)$
we obtain
for all
![]() $x\in L.$
It is clear that a is a generator of the different ideal
$x\in L.$
It is clear that a is a generator of the different ideal
![]() $\mathfrak {D}_{L/{\Bbb Q}_p} $
.
$\mathfrak {D}_{L/{\Bbb Q}_p} $
.
Let
![]() $dx$
be the Haar measure on L such that
$dx$
be the Haar measure on L such that
![]() $\int _{o_L}dx=1.$
Let
$\int _{o_L}dx=1.$
Let
![]() $\psi \colon L \to E^\times $
be a non-trivial character which kills an open subgroup of L.
$\psi \colon L \to E^\times $
be a non-trivial character which kills an open subgroup of L.
For a finite-dimensional E-linear representation D of the Weil-group
![]() $W_L:=W(\bar {L}/L)$
which is locally constant (i.e., the image of the inertia group is finite) we have local constants
$W_L:=W(\bar {L}/L)$
which is locally constant (i.e., the image of the inertia group is finite) we have local constants
see [Reference Deligne18] or [Reference Tate52] and [Reference Daigle and Flach16, §2.2].
If
![]() $\dim _E D=1$
corresponding to a locally constant homomorphism
$\dim _E D=1$
corresponding to a locally constant homomorphism
![]() $\delta :L^\times \to E^\times $
via local class field theory (see section 7.4 for the normalisation we choose), i.e.,
$\delta :L^\times \to E^\times $
via local class field theory (see section 7.4 for the normalisation we choose), i.e.,
![]() $D=E(\delta ),$
then
$D=E(\delta ),$
then
 $$ \begin{align} \epsilon_E(L,D,\psi_L,dx) &= \delta(\pi_L)^{a(\delta)} q^{n({\psi_L})} \sum_{i\in(o_L/\pi_L^{a(\delta)})^\times}\delta(i)^{-1} \psi_L(\frac{i}{\pi_L^{a(\delta)}}), \end{align} $$
$$ \begin{align} \epsilon_E(L,D,\psi_L,dx) &= \delta(\pi_L)^{a(\delta)} q^{n({\psi_L})} \sum_{i\in(o_L/\pi_L^{a(\delta)})^\times}\delta(i)^{-1} \psi_L(\frac{i}{\pi_L^{a(\delta)}}), \end{align} $$
 $$ \begin{align} \epsilon_E(L,D,\psi_u,dx) &= \delta(\pi_L)^{a(\delta)} q^{n(\psi_u)} \sum_{i\in(o_L/\pi_L^{a(\delta)})^\times}\delta(i)^{-1} \eta({i},u_{a(\delta)}). \end{align} $$
$$ \begin{align} \epsilon_E(L,D,\psi_u,dx) &= \delta(\pi_L)^{a(\delta)} q^{n(\psi_u)} \sum_{i\in(o_L/\pi_L^{a(\delta)})^\times}\delta(i)^{-1} \eta({i},u_{a(\delta)}). \end{align} $$
Here
![]() $n(\psi )$
denotes the largest integer n such that
$n(\psi )$
denotes the largest integer n such that
![]() $\pi _L^{-n}o_L\subseteq \ker {\psi }$
,
$\pi _L^{-n}o_L\subseteq \ker {\psi }$
,
![]() $a(\delta )$
denotes the conductor of
$a(\delta )$
denotes the conductor of
![]() $\delta ,$
(
$\delta ,$
(
![]() $0$
if
$0$
if
![]() $\delta $
is unramified, the smallest positive integer m such that
$\delta $
is unramified, the smallest positive integer m such that
![]() $1+\pi _L^mo_L\subseteq \ker \delta $
, if
$1+\pi _L^mo_L\subseteq \ker \delta $
, if
![]() $\delta $
is ramified). If
$\delta $
is ramified). If
![]() $W= (D,N)$
is a Weil Deligne representation of
$W= (D,N)$
is a Weil Deligne representation of
![]() $W_L$
with monodromy operator N and underlying Weil group representation D we modify, following Nakamura, its
$W_L$
with monodromy operator N and underlying Weil group representation D we modify, following Nakamura, its
![]() $\epsilon $
-constant by the factor
$\epsilon $
-constant by the factor
where
![]() $I_L$
denotes the inertia subgroup. Both definitions agree if N acts as
$I_L$
denotes the inertia subgroup. Both definitions agree if N acts as
![]() $0$
on
$0$
on
![]() $D.$
$D.$
Remark 6.2.
![]() $\psi _u(y)$
is independent of the choice of n such that
$\psi _u(y)$
is independent of the choice of n such that
![]() $y=x/\pi _L^n$
and
$y=x/\pi _L^n$
and
![]() $n(\psi _u)=0.$
$n(\psi _u)=0.$
Proof. The independence follows inductively from
![]() $\eta (\pi _Lx,u_{n}) = \eta (x,\varphi _L(u_{n})) = \eta (x,u_{n-1}).$
On the one hand, by definition
$\eta (\pi _Lx,u_{n}) = \eta (x,\varphi _L(u_{n})) = \eta (x,u_{n-1}).$
On the one hand, by definition
![]() $o_L \subset \ker \psi _u.$
On the other hand by §1, Fact 2 in [Reference Boxall8], using that
$o_L \subset \ker \psi _u.$
On the other hand by §1, Fact 2 in [Reference Boxall8], using that
![]() $u_1$
is a non-zero
$u_1$
is a non-zero
![]() $\pi _L$
-torsion point we may find
$\pi _L$
-torsion point we may find
![]() $a \in o_L$
such that
$a \in o_L$
such that
![]() $\psi _u(a/\pi _L)=\eta (a,u_1)$
is a primitive p-th root of unity. This proves that
$\psi _u(a/\pi _L)=\eta (a,u_1)$
is a primitive p-th root of unity. This proves that
![]() $\pi _L^{-1}o_L$
is not contained in
$\pi _L^{-1}o_L$
is not contained in
![]() $\ker (\psi _u).$
We conclude
$\ker (\psi _u).$
We conclude
![]() $n(\psi _u)=0.$
$n(\psi _u)=0.$
How do the epsilon-constants for the two choices
![]() $\psi _L$
and
$\psi _L$
and
![]() $\psi _u$
compare? The first choice behaves well under induction: there is a constant
$\psi _u$
compare? The first choice behaves well under induction: there is a constant
![]() $\lambda \in E$
depending on
$\lambda \in E$
depending on
![]() $L/{\Bbb Q}_p$
, the choices of Haar measures
$L/{\Bbb Q}_p$
, the choices of Haar measures
![]() $dx_{{\Bbb Q}_p}, dx_L $
and the choice of
$dx_{{\Bbb Q}_p}, dx_L $
and the choice of
![]() $\psi _0,$
such thatFootnote
19
$\psi _0,$
such thatFootnote
19
for all locally constant characters
![]() $\delta :L^\times \to E^\times $
(see [Reference Benois and Berger2] or [Reference Deligne18, (5.6)]).
$\delta :L^\times \to E^\times $
(see [Reference Benois and Berger2] or [Reference Deligne18, (5.6)]).
The second choice is obviously better adapted to the Lubin-Tate situation. By (55) there exists
![]() $a\in L^\times $
such that
$a\in L^\times $
such that
![]() $\psi _L( x)=\psi _u(ax)$
. Moreover, one knows that
$\psi _L( x)=\psi _u(ax)$
. Moreover, one knows that
![]() $\epsilon _E(L,\delta ,\psi _L(bx),dx_L)=\frac { \delta (b) }{ |b|}\epsilon _E(L,\delta ,\psi _L,dx_L)$
by [Reference Tate52, (3.2.3) or (3.4.4)] for all
$\epsilon _E(L,\delta ,\psi _L(bx),dx_L)=\frac { \delta (b) }{ |b|}\epsilon _E(L,\delta ,\psi _L,dx_L)$
by [Reference Tate52, (3.2.3) or (3.4.4)] for all
![]() $b\in L^\times $
. Combining the above we get the following:
$b\in L^\times $
. Combining the above we get the following:
Remark 6.3. There exists
![]() $\lambda \in E$
depending on
$\lambda \in E$
depending on
![]() $L/{\Bbb Q}_p$
, the choices of Haar measures
$L/{\Bbb Q}_p$
, the choices of Haar measures
![]() $dx_{{\Bbb Q}_p}, dx_L $
and the choice of
$dx_{{\Bbb Q}_p}, dx_L $
and the choice of
![]() $\psi _0$
, as well as
$\psi _0$
, as well as
![]() $a \in L^\times $
depending on
$a \in L^\times $
depending on
![]() $\psi _0$
and u such that
$\psi _0$
and u such that
 $$ \begin{align} \epsilon_E({\Bbb Q}_p,\mathrm{Ind}^L_{{\Bbb Q}_p}\delta,\psi_0,dx_{{\Bbb Q}_p})=\lambda \frac{ \delta(a) }{ |a|}\epsilon_E(L,\delta,\psi_u,dx_L) \end{align} $$
$$ \begin{align} \epsilon_E({\Bbb Q}_p,\mathrm{Ind}^L_{{\Bbb Q}_p}\delta,\psi_0,dx_{{\Bbb Q}_p})=\lambda \frac{ \delta(a) }{ |a|}\epsilon_E(L,\delta,\psi_u,dx_L) \end{align} $$
for all
![]() $\delta .$
$\delta .$
If we start with a Haar measure
![]() $dx$
of L, then the dual Haar measure
$dx$
of L, then the dual Haar measure
![]() $\hat {dx}$
with respect to the duality induced by
$\hat {dx}$
with respect to the duality induced by
![]() $\psi $
, i.e.,
$\psi $
, i.e.,
is the unique Haar measure such that
![]() $f(x)=\hat {\hat {f}}(-x)=\int _L \hat {f}(y)\psi (-xy)\hat {dx}(y)$
holds for all test functions in
$f(x)=\hat {\hat {f}}(-x)=\int _L \hat {f}(y)\psi (-xy)\hat {dx}(y)$
holds for all test functions in
![]() $L^1(L),$
where
$L^1(L),$
where
denotes the Fourier transform of
![]() $f.$
Especially for
$f.$
Especially for
![]() $f=\mathbf {1}_{\pi _L^{-n(\psi )}o_L}$
we obtain:
$f=\mathbf {1}_{\pi _L^{-n(\psi )}o_L}$
we obtain:
 $$ \begin{align*} \widehat{\mathbf{1}_{\pi_L^{-n(\psi)}o_L}}(y)= \left(\int_{\pi_L^{-n(\psi)}o_L} dx\right)\mathbf{1}_{o_L}(y), \end{align*} $$
$$ \begin{align*} \widehat{\mathbf{1}_{\pi_L^{-n(\psi)}o_L}}(y)= \left(\int_{\pi_L^{-n(\psi)}o_L} dx\right)\mathbf{1}_{o_L}(y), \end{align*} $$
whence
 $$ \begin{align*} \widehat{\widehat{\mathbf{1}_{\pi_L^{-n(\psi)}o_L}}}(-x)&=\left(\int_{\pi_L^{-n(\psi)}o_L} dx\right)\int_{o_L} \psi(-xy)\hat{dx}(y)\\ &=\left(\int_{\pi_L^{-n(\psi)}o_L} dx\right)\left(\int_{o_L}\hat{dx}(y)\right) \mathbf{1}_{_{\pi_L^{-n(\psi)}o_L}}(x), \end{align*} $$
$$ \begin{align*} \widehat{\widehat{\mathbf{1}_{\pi_L^{-n(\psi)}o_L}}}(-x)&=\left(\int_{\pi_L^{-n(\psi)}o_L} dx\right)\int_{o_L} \psi(-xy)\hat{dx}(y)\\ &=\left(\int_{\pi_L^{-n(\psi)}o_L} dx\right)\left(\int_{o_L}\hat{dx}(y)\right) \mathbf{1}_{_{\pi_L^{-n(\psi)}o_L}}(x), \end{align*} $$
i.e.,
![]() $\int _{o_L}\hat {dx}(y)=\frac {1}{q^{n(\psi )}} $
and
$\int _{o_L}\hat {dx}(y)=\frac {1}{q^{n(\psi )}} $
and
![]() $\hat {dx}=\frac {1}{q^{n(\psi )}}dx.$
$\hat {dx}=\frac {1}{q^{n(\psi )}}dx.$
From [Reference Tate52, (3.4.7)] we obtain
and similarly for higher rank representations D instead of
![]() $\delta .$
Since by (3.2.2/3) in (loc. cit.) we have
$\delta .$
Since by (3.2.2/3) in (loc. cit.) we have
![]() $\epsilon (L,\delta ,\psi ,rdx)=r\epsilon (L,\delta ,dx)$
for
$\epsilon (L,\delta ,\psi ,rdx)=r\epsilon (L,\delta ,dx)$
for
![]() $r>0$
and
$r>0$
and
![]() $\epsilon (L,\delta ,\psi (ax),dx)=\delta (a)|a|^{-1}\epsilon (L,\delta ,\psi (x),dx)$
, we conclude that
$\epsilon (L,\delta ,\psi (ax),dx)=\delta (a)|a|^{-1}\epsilon (L,\delta ,\psi (x),dx)$
, we conclude that
Moreover, by (3.4.5) in (loc. cit.) it holds that
7 Epsilon-isomorphisms - the statement of the conjecture
7.1 Determinant functor
Let R be a commutative ring. A graded invertible R-module is a pair
![]() $(\mathcal {L},r),$
where
$(\mathcal {L},r),$
where
![]() $\mathcal {L}$
is an invertible R-module and
$\mathcal {L}$
is an invertible R-module and
![]() $r: \operatorname {Spec}(R)\to \mathbb {Z}$
is a locally constant function. We define the category
$r: \operatorname {Spec}(R)\to \mathbb {Z}$
is a locally constant function. We define the category
![]() $\mathcal {P}_R$
of graded invertible R-modules by setting
$\mathcal {P}_R$
of graded invertible R-modules by setting
![]() $\operatorname {Mor}((\mathcal {L}_1,r),(\mathcal {L}_2,s)):=\operatorname {Isom}_R(\mathcal {L}_1,\mathcal {L}_2)$
if
$\operatorname {Mor}((\mathcal {L}_1,r),(\mathcal {L}_2,s)):=\operatorname {Isom}_R(\mathcal {L}_1,\mathcal {L}_2)$
if
![]() $r=s$
and empty otherwise. We further define
$r=s$
and empty otherwise. We further define
for each pair of objects and we identify
![]() $(\mathcal {L}_1,r)\otimes (\mathcal {L}_2,s)$
with
$(\mathcal {L}_1,r)\otimes (\mathcal {L}_2,s)$
with
![]() $(\mathcal {L}_2,s)\otimes (\mathcal {L}_1,r)$
via the morphism induced by
$(\mathcal {L}_2,s)\otimes (\mathcal {L}_1,r)$
via the morphism induced by
![]() $l_1\otimes l_2 \mapsto (-1)^{r+s}l_2 \otimes l_1.$
We denote by
$l_1\otimes l_2 \mapsto (-1)^{r+s}l_2 \otimes l_1.$
We denote by
![]() $\mathbf {1}_R$
the object
$\mathbf {1}_R$
the object
![]() $(R,0),$
which acts as a unit with respect to the tensor product and we remark that every object
$(R,0),$
which acts as a unit with respect to the tensor product and we remark that every object
![]() $(\mathcal {L},r)$
has an inverse given by
$(\mathcal {L},r)$
has an inverse given by
![]() $(\mathcal {L}^{-1},-r),$
where
$(\mathcal {L}^{-1},-r),$
where
![]() $\mathcal {L}^{-1}$
denotes the R-dual of
$\mathcal {L}^{-1}$
denotes the R-dual of
![]() $\mathcal {L}.$
For a ring morphism
$\mathcal {L}.$
For a ring morphism
![]() $R \to S$
and
$R \to S$
and
![]() $(\mathcal {L},r) \in \mathcal {P}_R$
we set
$(\mathcal {L},r) \in \mathcal {P}_R$
we set
![]() $(\mathcal {L},r)_{S}:=(\mathcal {L} \otimes S,r^*),$
where
$(\mathcal {L},r)_{S}:=(\mathcal {L} \otimes S,r^*),$
where
![]() $r^*$
denotes the pullback of r along
$r^*$
denotes the pullback of r along
![]() $R \to S.$
An isomorphism
$R \to S.$
An isomorphism
![]() $\mathbf {1}_R \to \mathcal {L}$
is called a trivialisation of
$\mathbf {1}_R \to \mathcal {L}$
is called a trivialisation of
![]() $\mathcal {L}.$
Let
$\mathcal {L}.$
Let
![]() $\mathcal {P}_{fg}(R)$
be the category of finitely generated projective R-modules and let
$\mathcal {P}_{fg}(R)$
be the category of finitely generated projective R-modules and let
![]() $(\mathcal {P}_{fg}(R),is)$
be its core, i.e. the subcategory consisting of the same objects with isomorphisms as morphisms. We have a functor
$(\mathcal {P}_{fg}(R),is)$
be its core, i.e. the subcategory consisting of the same objects with isomorphisms as morphisms. We have a functor
 $$ \begin{align*} \mathbf{d}_R\colon(\mathcal{P}_{fg}(R),is) &\to \mathcal{P}_R \\ P &\mapsto (\det P, \operatorname{rank}_R(P)), \end{align*} $$
$$ \begin{align*} \mathbf{d}_R\colon(\mathcal{P}_{fg}(R),is) &\to \mathcal{P}_R \\ P &\mapsto (\det P, \operatorname{rank}_R(P)), \end{align*} $$
where
![]() $\det P$
denotes the highest exterior power of
$\det P$
denotes the highest exterior power of
![]() $P.$
Note that
$P.$
Note that
![]() $\mathbf {d}_R$
is compatible with short exact sequences and base change in the sense that given an exact sequence
$\mathbf {d}_R$
is compatible with short exact sequences and base change in the sense that given an exact sequence
![]() $0 \to P_1 \to P_2 \to P_3\to 0$
the natural isomorphism
$0 \to P_1 \to P_2 \to P_3\to 0$
the natural isomorphism
induces an isomorphism
Moreover, for a morphism of rings
![]() $R \to S$
we have
$R \to S$
we have
![]() $\mathbf {d}_R(P)_{S} = \mathbf {d}_S(P\otimes S).$
This functor can be extended to the category
$\mathbf {d}_R(P)_{S} = \mathbf {d}_S(P\otimes S).$
This functor can be extended to the category
![]() $(\mathcal {C}^p(R),qis)$
of bounded complexes in
$(\mathcal {C}^p(R),qis)$
of bounded complexes in
![]() $\mathcal {P}(R)$
with quasi-isomorphisms as morphisms. On the level of objects this extension can be described as follows: Let
$\mathcal {P}(R)$
with quasi-isomorphisms as morphisms. On the level of objects this extension can be described as follows: Let
![]() $C^\bullet \in \mathcal {C}^p(R)$
then
$C^\bullet \in \mathcal {C}^p(R)$
then
This functor is again compatible with exact sequences and if
![]() $C^\bullet $
is acyclic, then the quasi isomorphism
$C^\bullet $
is acyclic, then the quasi isomorphism
![]() $0 \to C^\bullet $
induces a trivialisation of
$0 \to C^\bullet $
induces a trivialisation of
![]() $\mathbf {d}_R(C^\bullet )$
that we take as an identification. One can show that
$\mathbf {d}_R(C^\bullet )$
that we take as an identification. One can show that
![]() $\mathbf {d}_R$
factorises over
$\mathbf {d}_R$
factorises over
![]() $(\mathcal {D}^b_{\mathrm {perf}}(R),qis)$
, the image of the category of bounded complexes of finitely generated projective modules in the derived category with quasi isomorphisms as morphisms. If a complex
$(\mathcal {D}^b_{\mathrm {perf}}(R),qis)$
, the image of the category of bounded complexes of finitely generated projective modules in the derived category with quasi isomorphisms as morphisms. If a complex
![]() $C^\bullet $
is cohomologically perfect meaning that
$C^\bullet $
is cohomologically perfect meaning that
![]() $H^i(C^\bullet )$
considered as a complex concentrated in degree
$H^i(C^\bullet )$
considered as a complex concentrated in degree
![]() $0$
is in
$0$
is in
![]() $\mathcal {D}^b_{\mathrm {perf}}(R)$
for all i, then we have a canonical isomorphism
$\mathcal {D}^b_{\mathrm {perf}}(R)$
for all i, then we have a canonical isomorphism
that we take as an identification. This extension is further compatible with duality and base change in the following sense: There exist canonical isomorphisms
and
7.2 Fundamental lines
Let M be a
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_A,$
where A is an affinoid algebra over
$\mathcal {R}_A,$
where A is an affinoid algebra over
![]() $K.$
We assume that M satisfies the following technical condition:
$K.$
We assume that M satisfies the following technical condition:
where
![]() $\det M$
denotes the highest exterior power of
$\det M$
denotes the highest exterior power of
![]() $M.$
Clearly
$M.$
Clearly
![]() $\det M$
is always a module of rank
$\det M$
is always a module of rank
![]() $1$
and the technical condition is asking
$1$
and the technical condition is asking
![]() $\det M$
to be of character type up to a twist on the base. The full subcategory of
$\det M$
to be of character type up to a twist on the base. The full subcategory of
![]() $(\varphi _L,\Gamma _L)$
-modules satisfying the above contains all modules that arise as a base change from
$(\varphi _L,\Gamma _L)$
-modules satisfying the above contains all modules that arise as a base change from
![]() $\mathcal {R}_L$
by [Reference Fourquaux and Xie22, Proposition 1.9] and furthermore contains all trianguline modules (even with
$\mathcal {R}_L$
by [Reference Fourquaux and Xie22, Proposition 1.9] and furthermore contains all trianguline modules (even with
![]() $\mathcal {L}=A$
). If M satisfies the above condition the isomorphism class of
$\mathcal {L}=A$
). If M satisfies the above condition the isomorphism class of
![]() $\mathcal {L}$
and the character
$\mathcal {L}$
and the character
![]() $\delta $
are uniquely determined. Furthermore
$\delta $
are uniquely determined. Furthermore
![]() $\mathcal {L}$
can be identified with the subset
$\mathcal {L}$
can be identified with the subset
by sending
![]() $l\in \mathcal {L}$
to
$l\in \mathcal {L}$
to
![]() $l\otimes \mathbf {e}_\delta \in \mathcal {L} \otimes _A \mathcal {R}_A(\delta ).$
$l\otimes \mathbf {e}_\delta \in \mathcal {L} \otimes _A \mathcal {R}_A(\delta ).$
Definition 7.1. Let M be an L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module of rank
$(\varphi _L,\Gamma _L)$
-module of rank
![]() $r_M$
over
$r_M$
over
![]() $\mathcal {R}_A$
satisfying (63). Write
$\mathcal {R}_A$
satisfying (63). Write
![]() $\det (M) = \mathcal {L} \otimes \mathcal {R}_A( \delta _{\det M}).$
We define
$\det (M) = \mathcal {L} \otimes \mathcal {R}_A( \delta _{\det M}).$
We define
using Remark (4.8), and
 $$ \begin{align*}\Delta_{2,A}(M):= \bigg(\{x \in \det M \mid \varphi_L(x)= \delta_{\det M}(\pi_L)x, \gamma x = \delta_{\det M}(\gamma)x\}, -\chi_{A[\Gamma_L/U]}(K_{\varphi,D(U,K)}(M))\bigg),\end{align*} $$
$$ \begin{align*}\Delta_{2,A}(M):= \bigg(\{x \in \det M \mid \varphi_L(x)= \delta_{\det M}(\pi_L)x, \gamma x = \delta_{\det M}(\gamma)x\}, -\chi_{A[\Gamma_L/U]}(K_{\varphi,D(U,K)}(M))\bigg),\end{align*} $$
i.e., the underlying line bundle of
![]() $\Delta _{2,A}$
is
$\Delta _{2,A}$
is
![]() $\mathcal {L}$
which has a canonical
$\mathcal {L}$
which has a canonical
![]() $(\varphi _L,\Gamma _L)$
-action given by
$(\varphi _L,\Gamma _L)$
-action given by
![]() $\delta _{\det M},$
. We also write
$\delta _{\det M},$
. We also write
![]() $\mathcal {L}(\delta _{\det M})$
if we wish to emphasize the action.
$\mathcal {L}(\delta _{\det M})$
if we wish to emphasize the action.
Remark 7.2. We have
whence
![]() $\Delta _{2,K}(\mathcal {R}_K(\delta ))=(K\mathbf {e}_\delta ,1)\cong (K,1)$
using Remark 4.7.
$\Delta _{2,K}(\mathcal {R}_K(\delta ))=(K\mathbf {e}_\delta ,1)\cong (K,1)$
using Remark 4.7.
Proposition 7.3.
![]() $\Delta _{1,A}(M)$
and
$\Delta _{1,A}(M)$
and
![]() $\Delta _{2,A}(M)$
are well-defined graded invertible modules and
$\Delta _{2,A}(M)$
are well-defined graded invertible modules and
satisfies the following properties
-
(i) For any continuous map of affinoid algebras
 $A \to B$
induces a canonical isomorphism
$A \to B$
induces a canonical isomorphism  $$ \begin{align*}\Delta_A(M)\otimes_AB \cong \Delta_B(M\hat{\otimes}_AB).\end{align*} $$
$$ \begin{align*}\Delta_A(M)\otimes_AB \cong \Delta_B(M\hat{\otimes}_AB).\end{align*} $$
-
(ii)
 $\Delta _A(M)$
is multiplicative in short exact sequences.
$\Delta _A(M)$
is multiplicative in short exact sequences. -
(iii)
 $ \Delta _A(M) \cong \Delta _A(\tilde {M})^*\otimes (A(\chi ^{r_M}),0).$
$ \Delta _A(M) \cong \Delta _A(\tilde {M})^*\otimes (A(\chi ^{r_M}),0).$
Proof. Compatibility with base change can be checked for
![]() $\Delta _{i}:=\Delta _{i,A}$
individually. For
$\Delta _{i}:=\Delta _{i,A}$
individually. For
![]() $\Delta _{1}$
it follows from Theorem 4.6 and for
$\Delta _{1}$
it follows from Theorem 4.6 and for
![]() $\Delta _2$
it is clear. The compatibility with short exact sequences can also be checked individually for
$\Delta _2$
it is clear. The compatibility with short exact sequences can also be checked individually for
![]() $\Delta _{i}.$
For
$\Delta _{i}.$
For
![]() $i=2$
it follows from the corresponding statement for determinants and for
$i=2$
it follows from the corresponding statement for determinants and for
![]() $i=1$
it follows from the fact that a short exact sequence of
$i=1$
it follows from the fact that a short exact sequence of
![]() $(\varphi _L,U)$
-modules induces a short exact sequence of the complexes
$(\varphi _L,U)$
-modules induces a short exact sequence of the complexes
![]() $K_{f,D(U,K)}.$
The quasi-isomorphism
$K_{f,D(U,K)}.$
The quasi-isomorphism
![]() $\digamma (M):{K_{\varphi ,{{\mathfrak {Z}}}}(M)}\cong K_{\varphi ,{\mathfrak {Z}}}(\tilde {M} )^*[-2]$
induced from (24) by identifying
$\digamma (M):{K_{\varphi ,{{\mathfrak {Z}}}}(M)}\cong K_{\varphi ,{\mathfrak {Z}}}(\tilde {M} )^*[-2]$
induced from (24) by identifying
![]() $\tilde {\tilde {M}}\cong M$
gives an isomorphism
$\tilde {\tilde {M}}\cong M$
gives an isomorphism
![]() $\Delta _{?,1}(M)\cong \Delta _{?,1}(\tilde {M})^*$
while the isomorphism
$\Delta _{?,1}(M)\cong \Delta _{?,1}(\tilde {M})^*$
while the isomorphism
![]() $\Delta _{A,2}(M)\cong \Delta _{A,2}(\tilde {M})^*\otimes (A(\chi ^{r_M}),0)$
arises as follows: First observe that
$\Delta _{A,2}(M)\cong \Delta _{A,2}(\tilde {M})^*\otimes (A(\chi ^{r_M}),0)$
arises as follows: First observe that
![]() $\tilde {M}$
satisfies (63), if M does, and since
$\tilde {M}$
satisfies (63), if M does, and since
![]() $\tilde {M} = A(\chi ) \otimes _A M^*$
one sees that
$\tilde {M} = A(\chi ) \otimes _A M^*$
one sees that
![]() $\det (\tilde {M}) \cong A(\chi ^{\operatorname {rk}(M)}) \otimes \det (M^*).$
Hence we see
$\det (\tilde {M}) \cong A(\chi ^{\operatorname {rk}(M)}) \otimes \det (M^*).$
Hence we see
![]() $\Delta _{A,2}(\tilde {M}) = \Delta _{A,2}(M^*) \otimes A(\chi ^r).$
A small calculation shows
$\Delta _{A,2}(\tilde {M}) = \Delta _{A,2}(M^*) \otimes A(\chi ^r).$
A small calculation shows
![]() $\Delta _{A,2}(M^*)= \Delta _{A,2}(M)^*,$
hence the claim.
$\Delta _{A,2}(M^*)= \Delta _{A,2}(M)^*,$
hence the claim.
Definition 7.4. Let X be a rigid analytic space over
![]() $K.$
Given a family of
$K.$
Given a family of
![]() $(\varphi _L,\Gamma _L)$
-modules M over
$(\varphi _L,\Gamma _L)$
-modules M over
![]() $\mathcal {O}_X,$
i.e., a compatible collection of
$\mathcal {O}_X,$
i.e., a compatible collection of
![]() $(\varphi _L,\Gamma _L)$
-modules
$(\varphi _L,\Gamma _L)$
-modules
![]() $M_A$
over
$M_A$
over
![]() $\mathcal {R}_A$
for every affinoid
$\mathcal {R}_A$
for every affinoid
![]() $\operatorname {Sp}(A)\subseteq X$
, we define
$\operatorname {Sp}(A)\subseteq X$
, we define
![]() $\Delta _X(M)$
as the global sections of the line-bundle
$\Delta _X(M)$
as the global sections of the line-bundle
![]() $\mathfrak {D}_X(M)$
defined by
$\mathfrak {D}_X(M)$
defined by
![]() $\operatorname {Sp}(A) \mapsto \Delta _{A}(M_A).$
If X is quasi-Stein covered by an increasing union
$\operatorname {Sp}(A) \mapsto \Delta _{A}(M_A).$
If X is quasi-Stein covered by an increasing union
![]() $X_n$
of affinoids we also have
$X_n$
of affinoids we also have
![]() $\Delta _X(M)[0]=\operatorname {R}\Gamma (X,\mathfrak {D}_X(M))=\operatorname {Rlim}(\Delta _{X_n}(M_{X_n})) \cong \lim \Delta _{X_n}(M_{X_n})[0]$
by Theorem B for quasi-Stein spaces. We have analogous definitions and statements for
$\Delta _X(M)[0]=\operatorname {R}\Gamma (X,\mathfrak {D}_X(M))=\operatorname {Rlim}(\Delta _{X_n}(M_{X_n})) \cong \lim \Delta _{X_n}(M_{X_n})[0]$
by Theorem B for quasi-Stein spaces. We have analogous definitions and statements for
![]() $\Delta _{i,X}(M)$
and
$\Delta _{i,X}(M)$
and
![]() $\mathfrak {D}_{i,X}, i=1,2$
respectively.
$\mathfrak {D}_{i,X}, i=1,2$
respectively.
![]() $\mathfrak {D}_X,\mathfrak {D}_{i,X}$
are graded invertible
$\mathfrak {D}_X,\mathfrak {D}_{i,X}$
are graded invertible
![]() $\mathcal {O}_X$
-modules by definition.
$\mathcal {O}_X$
-modules by definition.
A word of caution is in order. A priori the
![]() $\Delta _{i,X}(M)$
are not necessarily graded invertible
$\Delta _{i,X}(M)$
are not necessarily graded invertible
![]() $\mathcal {O}_X(X)$
-modules because the global sections do not have to be finitely generated over
$\mathcal {O}_X(X)$
-modules because the global sections do not have to be finitely generated over
![]() $\mathcal {O}_X.$
In our applications (in section 8) we will have
$\mathcal {O}_X.$
In our applications (in section 8) we will have
![]() $\Delta _{2,X} = \mathcal {O}_X(X)$
and will be in a position to apply the subsequent remark in order to conclude that
$\Delta _{2,X} = \mathcal {O}_X(X)$
and will be in a position to apply the subsequent remark in order to conclude that
![]() $\Delta _{1,X}$
is an invertible
$\Delta _{1,X}$
is an invertible
![]() $\mathcal {O}_X(X)$
-module.
$\mathcal {O}_X(X)$
-module.
Remark 7.5. Let
![]() $ X = \bigcup X_n$
be a quasi-Stein space. Let
$ X = \bigcup X_n$
be a quasi-Stein space. Let
![]() $C_n^\bullet $
be a family of perfect complexes of
$C_n^\bullet $
be a family of perfect complexes of
![]() $\mathcal {O}_{X}(X_n)$
-modules together with quasi-isomorphisms
$\mathcal {O}_{X}(X_n)$
-modules together with quasi-isomorphisms
![]() $\mathcal {O}_{X}(X_{n-1}) \otimes ^{\mathbb {L}}_{\mathcal {O}_{X}(X_n)} C^\bullet _n \simeq C^\bullet _{n-1}.$
Assume that there exists a perfect complex
$\mathcal {O}_{X}(X_{n-1}) \otimes ^{\mathbb {L}}_{\mathcal {O}_{X}(X_n)} C^\bullet _n \simeq C^\bullet _{n-1}.$
Assume that there exists a perfect complex
![]() $C^\bullet $
of
$C^\bullet $
of
![]() $\mathcal {O}_X(X)$
-modules (in the ring-theoretic senseFootnote
20
) such that
$\mathcal {O}_X(X)$
-modules (in the ring-theoretic senseFootnote
20
) such that
![]() $\mathcal {O}_{X}(X_n) \otimes ^{\mathbb {L}}_{\mathcal {O}_{X}(X)} C^\bullet \simeq C^\bullet _{n}$
.
$\mathcal {O}_{X}(X_n) \otimes ^{\mathbb {L}}_{\mathcal {O}_{X}(X)} C^\bullet \simeq C^\bullet _{n}$
.
Then we have
![]() $\mathbf {d}_{\mathcal {O}_{X}(X_n)}(C^\bullet _n)\cong \mathcal {O}_{X}(X_n)\otimes \mathbf {d}_{\mathcal {O}_X(X)}(C^\bullet )$
. Furthermore
$\mathbf {d}_{\mathcal {O}_{X}(X_n)}(C^\bullet _n)\cong \mathcal {O}_{X}(X_n)\otimes \mathbf {d}_{\mathcal {O}_X(X)}(C^\bullet )$
. Furthermore
![]() $\mathbf {d}_{\mathcal {O}_X(X)}(C^\bullet )$
is coadmissible, i.e.,
$\mathbf {d}_{\mathcal {O}_X(X)}(C^\bullet )$
is coadmissible, i.e.,
![]() $\mathbf {d}_{\mathcal {O}_X(X)}(C^\bullet ) = \varprojlim _n \mathbf {d}_{\mathcal {O}_{X}(X_n)}(C_n^\bullet ).$
$\mathbf {d}_{\mathcal {O}_X(X)}(C^\bullet ) = \varprojlim _n \mathbf {d}_{\mathcal {O}_{X}(X_n)}(C_n^\bullet ).$
Proof. The proof is formal using that determinant functors commute with derived tensor products and
![]() $\mathcal {O}_{X}(X_n) \to \mathcal {O}_{X}(X_{n-1})$
is flat together with the fact that
$\mathcal {O}_{X}(X_n) \to \mathcal {O}_{X}(X_{n-1})$
is flat together with the fact that
![]() $\mathbf {d}(C^\bullet )$
is a rank one projective module over
$\mathbf {d}(C^\bullet )$
is a rank one projective module over
![]() $\mathcal {O}_X(X)$
and hence coadmissible by [Reference Schneider and Teitelbaum43, Corollary 3.4].
$\mathcal {O}_X(X)$
and hence coadmissible by [Reference Schneider and Teitelbaum43, Corollary 3.4].
7.3 Statement
We expect that the results in section 4 extend to affinoids (where only stated or proven over fields) and to all analytic
![]() $(\varphi _L,\Gamma _L)$
-modules (where only stated for rank one or trianguline ones), explicitly this refers to Remark 4.7 and Theorems 4.9, 4.10, 4.16. Hence we state the conjecture below in this level of generality.
$(\varphi _L,\Gamma _L)$
-modules (where only stated for rank one or trianguline ones), explicitly this refers to Remark 4.7 and Theorems 4.9, 4.10, 4.16. Hence we state the conjecture below in this level of generality.
Conjecture 7.6. Choose a compatible system
![]() $u=(u_n)$
of
$u=(u_n)$
of
![]() $[\pi _L^n]$
-torsion points of the Lubin-Tate group and a generator
$[\pi _L^n]$
-torsion points of the Lubin-Tate group and a generator
![]() $t^{\prime }_0$
of
$t^{\prime }_0$
of
![]() $T_\pi '$
. Let A be an affinoid algebra over
$T_\pi '$
. Let A be an affinoid algebra over
![]() $K,$
a complete field extension of L containing
$K,$
a complete field extension of L containing
![]() $L^{ab}.$
For each L-analytic
$L^{ab}.$
For each L-analytic
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_A$
satisfying condition (63) there exists a unique trivialisation
$\mathcal {R}_A$
satisfying condition (63) there exists a unique trivialisation
satisfying the following axioms:
-
(i) For any affinoid algebra B over A we have
under the canonical isomorphism $$ \begin{align*}\varepsilon_{A,u}(M)\otimes_A \operatorname{id}_B = \varepsilon_{B,u}(M\hat{\otimes}_AB)\end{align*} $$
$$ \begin{align*}\varepsilon_{A,u}(M)\otimes_A \operatorname{id}_B = \varepsilon_{B,u}(M\hat{\otimes}_AB)\end{align*} $$
 $\Delta _A(M)\otimes _AB \cong \Delta _B(M\hat {\otimes }_AB).$
$\Delta _A(M)\otimes _AB \cong \Delta _B(M\hat {\otimes }_AB).$
-
(ii)
 $\varepsilon _{A,u}$
is multiplicative in short exact sequences.
$\varepsilon _{A,u}$
is multiplicative in short exact sequences. -
(iii) For any
 $a \in o_L^\times $
we have
$a \in o_L^\times $
we have  $$ \begin{align*}\varepsilon_{A,a \cdot u}(M)=\delta_{\det M}(a)\varepsilon_{A,u}.\end{align*} $$
$$ \begin{align*}\varepsilon_{A,a \cdot u}(M)=\delta_{\det M}(a)\varepsilon_{A,u}.\end{align*} $$
-
(iv)
 $\varepsilon _{A,u}(M)$
is compatible with duality in the sense that under the natural isomorphisms
$\varepsilon _{A,u}(M)$
is compatible with duality in the sense that under the natural isomorphisms $$ \begin{align*}\varepsilon_{A,u}(\tilde{M})^* \otimes h(\chi^{r_M}) = (-1)^{\dim_KH^0(M)}\Omega_{t^{\prime}_0}^{-r_{M}} \varepsilon_{A,-u}(M)\end{align*} $$
$$ \begin{align*}\varepsilon_{A,u}(\tilde{M})^* \otimes h(\chi^{r_M}) = (-1)^{\dim_KH^0(M)}\Omega_{t^{\prime}_0}^{-r_{M}} \varepsilon_{A,-u}(M)\end{align*} $$
 $\mathbf {1}_A \cong \mathbf {1}_A \otimes \mathbf {1}_A$
and
$\mathbf {1}_A \cong \mathbf {1}_A \otimes \mathbf {1}_A$
and
 $\Delta (M)\cong \Delta (\tilde {M})^* \otimes (A(r_M),0),$
where
$\Delta (M)\cong \Delta (\tilde {M})^* \otimes (A(r_M),0),$
where
 $h(\chi ^{r_M}) \colon A(r_M) \to A$
maps
$h(\chi ^{r_M}) \colon A(r_M) \to A$
maps
 $e_{\chi ^{r_M}}$
to
$e_{\chi ^{r_M}}$
to
 $1.$
$1.$
-
(v) For
 $L=\mathbb {Q}_p$
,
$L=\mathbb {Q}_p$
,
 $\pi _L=p$
and
$\pi _L=p$
and
 $u=(\zeta _{p^n}-1)_n$
the trivialisation coincides with that of Nakamura, in the sense of Proposition 8.7.
$u=(\zeta _{p^n}-1)_n$
the trivialisation coincides with that of Nakamura, in the sense of Proposition 8.7. -
(vi) Let
 $F/L$
be a finite subextension of
$F/L$
be a finite subextension of
 $K, M_0$
be a de Rham
$K, M_0$
be a de Rham
 $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
 $\mathcal {R}_F$
and
$\mathcal {R}_F$
and
 $M = K\hat {\otimes }_FM_0.$
Then
$M = K\hat {\otimes }_FM_0.$
Then  $$ \begin{align*}\varepsilon_{K,u}(M)=\varepsilon^{dR}_{F,u}(M_0).\end{align*} $$
$$ \begin{align*}\varepsilon_{K,u}(M)=\varepsilon^{dR}_{F,u}(M_0).\end{align*} $$
Remark 7.7.
-
(i) The occurrence of the power of
 $\Omega $
in the compatibility with duality (iv) is a conceptually new phenomenon in our conjecture, see also Proposition 7.14.
$\Omega $
in the compatibility with duality (iv) is a conceptually new phenomenon in our conjecture, see also Proposition 7.14. -
(ii) Due to the equivalence of categories stated in [Reference Berger, Schneider and Xie7, Thm. 3.16] there is an analogous conjecture for L-analytic
 $(\varphi _L,\Gamma _L)$
-modules over the character variety, i.e., by replacing the usual Robba ring
$(\varphi _L,\Gamma _L)$
-modules over the character variety, i.e., by replacing the usual Robba ring
 $\mathcal {R}_K=\mathcal {R}_K(\mathbf {B})$
(attached to the open unit ball
$\mathcal {R}_K=\mathcal {R}_K(\mathbf {B})$
(attached to the open unit ball
 $\mathbf {B}$
) by the Robba ring
$\mathbf {B}$
) by the Robba ring
 $\mathcal {R}_K(\mathfrak {X}_{o_L} )$
of the character variety
$\mathcal {R}_K(\mathfrak {X}_{o_L} )$
of the character variety
 $\mathfrak {X}_{o_L}$
attached to the group
$\mathfrak {X}_{o_L}$
attached to the group
 $o_L$
, see [Reference Berger, Schneider and Xie7, §2.4] or [Reference Schneider and Venjakob46, §4.3.6]. In this situation, we expect that the conditions concerning K can be weakened and perhaps the descent to L (or any finite extension of it) instead of the huge field K should be feasible, compare with Thm. 4.3.23 in (loc. cit.). Moreover, due to [Reference Schneider and Venjakob46, Lem. 4.3.25] there should be no occurrence of
$o_L$
, see [Reference Berger, Schneider and Xie7, §2.4] or [Reference Schneider and Venjakob46, §4.3.6]. In this situation, we expect that the conditions concerning K can be weakened and perhaps the descent to L (or any finite extension of it) instead of the huge field K should be feasible, compare with Thm. 4.3.23 in (loc. cit.). Moreover, due to [Reference Schneider and Venjakob46, Lem. 4.3.25] there should be no occurrence of
 $\Omega $
! We will pursue this in future work.
$\Omega $
! We will pursue this in future work. -
(iii) The assumption that K contains
 $\widehat {L^{ab}}$
can be dropped in the case that
$\widehat {L^{ab}}$
can be dropped in the case that
 $L=\mathbb {Q}_p$
as the period
$L=\mathbb {Q}_p$
as the period
 $\Omega _{\mathbb {Q}_p}$
can be taken to be any element in
$\Omega _{\mathbb {Q}_p}$
can be taken to be any element in
 $\mathbb {Z}_p^\times .$
In order to specialise our construction to Nakamura’s one has to make more specific choices. Fixing an element
$\mathbb {Z}_p^\times .$
In order to specialise our construction to Nakamura’s one has to make more specific choices. Fixing an element
 $\gamma \in \Gamma ,$
whose image in
$\gamma \in \Gamma ,$
whose image in
 $\Gamma /\Gamma _{p-\text {power-torsion}}$
is a topological generator implicitly determines the period as
$\Gamma /\Gamma _{p-\text {power-torsion}}$
is a topological generator implicitly determines the period as
 $\Omega _{\mathbb {Q}_p}= \log _0(\chi _{cyc}(\gamma ))^{-1}.$
But this would not necessarily be compatible with Nakamura’s variant of the de Rham isomorphism, since his variant does not involve any period. Instead one should choose a
$\Omega _{\mathbb {Q}_p}= \log _0(\chi _{cyc}(\gamma ))^{-1}.$
But this would not necessarily be compatible with Nakamura’s variant of the de Rham isomorphism, since his variant does not involve any period. Instead one should choose a
 $\gamma $
such that
$\gamma $
such that
 $\log _0(\chi _{cyc}(\gamma ))=1.$
This defect is due to the fact our variant of the exponential map involves the period
$\log _0(\chi _{cyc}(\gamma ))=1.$
This defect is due to the fact our variant of the exponential map involves the period
 $\Omega $
as part of its definition and hence so does our de Rham isomorphism. This is not a contradiction to the uniqueness of the
$\Omega $
as part of its definition and hence so does our de Rham isomorphism. This is not a contradiction to the uniqueness of the
 $\varepsilon $
-isomorphisms in question. Indeed in the rank one case, we can see the
$\varepsilon $
-isomorphisms in question. Indeed in the rank one case, we can see the
 $\varepsilon $
-isomorphism is determined by its behaviour at de Rham points. If
$\varepsilon $
-isomorphism is determined by its behaviour at de Rham points. If
 $\Omega _{\mathbb {Q}_p} \neq 1$
then our variant asks for a different behaviour at these de Rham points thus leading to a different result.
$\Omega _{\mathbb {Q}_p} \neq 1$
then our variant asks for a different behaviour at these de Rham points thus leading to a different result.
7.4 The de Rham case
In this section we explain how to attach a Weil-Deligne Representation to an L-analytic de Rham
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_L$
in order to define the de Rham epsilon-constants. We denote by
$\mathcal {R}_L$
in order to define the de Rham epsilon-constants. We denote by
![]() $\mathbf {B}_{?}$
for
$\mathbf {B}_{?}$
for
![]() $? \in \{\mathrm {cris},\mathrm {dR},\mathrm {st}\}$
Fontaine’s usual period rings. Without difficulty this construction can be generalised to
$? \in \{\mathrm {cris},\mathrm {dR},\mathrm {st}\}$
Fontaine’s usual period rings. Without difficulty this construction can be generalised to
![]() $(\varphi _L,\Gamma _L)$
-modules over
$(\varphi _L,\Gamma _L)$
-modules over
![]() $F \otimes _L \mathcal {R}_L$
for a finite extension F with trivial action. In order to keep notation light we will assume without loss of generality
$F \otimes _L \mathcal {R}_L$
for a finite extension F with trivial action. In order to keep notation light we will assume without loss of generality
![]() $F=L.$
We write
$F=L.$
We write
![]() $\mathbf {B}_{e,LT}=\tilde {\mathcal {R}}[1/t_{LT}]^{\varphi _L=1}.$
We will make use of the equivalence of categories between L-analytic
$\mathbf {B}_{e,LT}=\tilde {\mathcal {R}}[1/t_{LT}]^{\varphi _L=1}.$
We will make use of the equivalence of categories between L-analytic
![]() $(\varphi _L,\Gamma _L)$
-modules and L-analytic B-pairs originally suggested in [Reference Berger5, Remark 10.3] and detailed in [Reference Poyeton39, Theorem 5.5]. A priori these results are only applicable to E-linear representations of
$(\varphi _L,\Gamma _L)$
-modules and L-analytic B-pairs originally suggested in [Reference Berger5, Remark 10.3] and detailed in [Reference Poyeton39, Theorem 5.5]. A priori these results are only applicable to E-linear representations of
![]() $G_L,$
where E denotes a Galois closure of
$G_L,$
where E denotes a Galois closure of
![]() $L/\mathbb {Q}_p.$
If we start with an analytic
$L/\mathbb {Q}_p.$
If we start with an analytic
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_L$
then by [Reference Poyeton39] we can attach to
$\mathcal {R}_L$
then by [Reference Poyeton39] we can attach to
![]() $E \otimes _L M$
a B-pair (called
$E \otimes _L M$
a B-pair (called
![]() $B_{\operatorname {id}}$
-pair in (loc. cit.)), i.e., a pair consisting of a finite free
$B_{\operatorname {id}}$
-pair in (loc. cit.)), i.e., a pair consisting of a finite free
![]() $E\otimes _L\mathbf {B}_{dR}^+$
-module
$E\otimes _L\mathbf {B}_{dR}^+$
-module
![]() $W^+_{dR,\operatorname {id},E}$
with a
$W^+_{dR,\operatorname {id},E}$
with a
![]() $\mathbf {B}_{dR}^+$
-semi-linear (and E-linear)
$\mathbf {B}_{dR}^+$
-semi-linear (and E-linear)
![]() $G_L$
-action and a finite free
$G_L$
-action and a finite free
![]() $\mathbf {B}_{e,LT,E}:= E\otimes _L\mathbf {B}_{e,LT}$
-module
$\mathbf {B}_{e,LT,E}:= E\otimes _L\mathbf {B}_{e,LT}$
-module
![]() $W^{LT}_{\operatorname {id},E}$
with semi-linear
$W^{LT}_{\operatorname {id},E}$
with semi-linear
![]() $G_L$
-action together with an isomorphism after base change to
$G_L$
-action together with an isomorphism after base change to
![]() $\mathbf {B}_{dR}.$
By Galois descent, taking invariants with respect to the
$\mathbf {B}_{dR}.$
By Galois descent, taking invariants with respect to the
![]() $G(E/L)$
-action (acting via the first tensor factor) provides us with a B-pair
$G(E/L)$
-action (acting via the first tensor factor) provides us with a B-pair
![]() $W(M):=(W_{dR}^+(M),W_e(M))$
over
$W(M):=(W_{dR}^+(M),W_e(M))$
over
![]() $(\mathbf {B}_{dR}^+,\mathbf {B}_{e,LT}).$
The ring
$(\mathbf {B}_{dR}^+,\mathbf {B}_{e,LT}).$
The ring
![]() $\mathbf {B}_{e,LT}$
can be viewed as a subring of
$\mathbf {B}_{e,LT}$
can be viewed as a subring of
![]() $\mathbf {B}_{\mathrm {cris},L}.$
Indeed, since
$\mathbf {B}_{\mathrm {cris},L}.$
Indeed, since
![]() $\varphi (t_{LT}) = \pi _L t_{LT}$
it suffices to consider elements of
$\varphi (t_{LT}) = \pi _L t_{LT}$
it suffices to consider elements of
![]() $\tilde {\mathcal {R}}$
satisfying
$\tilde {\mathcal {R}}$
satisfying
![]() $\varphi (x) = \pi _L^jx$
for some
$\varphi (x) = \pi _L^jx$
for some
![]() $j \in \mathbb {Z},$
which by Frobenius regularisation are already contained in
$j \in \mathbb {Z},$
which by Frobenius regularisation are already contained in
![]() $\tilde {\mathcal {R}}^+$
(cf. [Reference Berger3, Proposition 3.2] in the cyclotomic case, and a similar result holds for ramified Witt-vectors as well (cf. [Reference Steingart49, Satz 3.19])). The ring
$\tilde {\mathcal {R}}^+$
(cf. [Reference Berger3, Proposition 3.2] in the cyclotomic case, and a similar result holds for ramified Witt-vectors as well (cf. [Reference Steingart49, Satz 3.19])). The ring
![]() $\tilde {\mathcal {R}}^+$
is a subring of
$\tilde {\mathcal {R}}^+$
is a subring of
![]() $\mathbf {B}_{\mathrm {cris},L}.$
We call a B-pair
$\mathbf {B}_{\mathrm {cris},L}.$
We call a B-pair
![]() $(W_{dR}^+,W_e)$
de Rham if
$(W_{dR}^+,W_e)$
de Rham if
![]() $W_{dR}^+[1/t_{LT}]$
admits a
$W_{dR}^+[1/t_{LT}]$
admits a
![]() $G_L$
-invariant basis. One can show, that this is equivalent to the corresponding
$G_L$
-invariant basis. One can show, that this is equivalent to the corresponding
![]() $(\varphi _L,\Gamma _L)$
-module being de Rham (cf. [Reference Porat38, Section 3.2, Proposition 3.7] for a proof in the étale case). Note that our notion of de Rham coincides with L-de Rham in loc. cit.). Consider for
$(\varphi _L,\Gamma _L)$
-module being de Rham (cf. [Reference Porat38, Section 3.2, Proposition 3.7] for a proof in the étale case). Note that our notion of de Rham coincides with L-de Rham in loc. cit.). Consider for
![]() $F/L$
finite the vector space
$F/L$
finite the vector space
over the maximal unramified subextension
![]() $F'$
of
$F'$
of
![]() $F/L$
. We define
$F/L$
. We define
![]() $D_{\mathrm {pst}}(M)$
as their colimit over all
$D_{\mathrm {pst}}(M)$
as their colimit over all
![]() $F/L$
finite. By a standard argument (cf. proof of Theorem 2.13 Part (1) in [Reference Fontaine and Ouyang20]), each
$F/L$
finite. By a standard argument (cf. proof of Theorem 2.13 Part (1) in [Reference Fontaine and Ouyang20]), each
![]() $F'$
-vector space
$F'$
-vector space
![]() $D_{st}(M_{\mid F})$
is of dimension
$D_{st}(M_{\mid F})$
is of dimension
![]() $\leq \operatorname {rk} M$
and
$\leq \operatorname {rk} M$
and
![]() $D_{pst}(M)$
is hence an
$D_{pst}(M)$
is hence an
![]() $L^{nr}$
-vector space of dimension
$L^{nr}$
-vector space of dimension
![]() $\leq \operatorname {rk} M.$
We say that M is potentially semi-stable if this dimension is precisely
$\leq \operatorname {rk} M.$
We say that M is potentially semi-stable if this dimension is precisely
![]() $\operatorname {rk} M$
or, equivalently, if there exists a finite extension
$\operatorname {rk} M$
or, equivalently, if there exists a finite extension
![]() $F/L$
such that
$F/L$
such that
![]() $D_{st}(M_{\mid F})$
is an
$D_{st}(M_{\mid F})$
is an
![]() $F'$
-vector space of dimension
$F'$
-vector space of dimension
![]() $\operatorname {rk} M.$
The p-adic monodromy theorem also holds for B-pairs in the cyclotomic case and there is an obvious L-analytic analogue providing us with the following (see [Reference Porat38, Corollary 3.10] for a treatment in the étale case).
$\operatorname {rk} M.$
The p-adic monodromy theorem also holds for B-pairs in the cyclotomic case and there is an obvious L-analytic analogue providing us with the following (see [Reference Porat38, Corollary 3.10] for a treatment in the étale case).
Remark 7.8. M is de Rham if and only if M is potentially semi-stable.
Note that
![]() $D_{\mathrm {pst}}(M)$
naturally has a semi-linear
$D_{\mathrm {pst}}(M)$
naturally has a semi-linear
![]() $G_L$
-action and inherits from
$G_L$
-action and inherits from
![]() $\mathbf {B}_{\mathrm {st},L}=\mathbf {B}_{\mathrm {st}}\otimes _{L_0}L$
an action of
$\mathbf {B}_{\mathrm {st},L}=\mathbf {B}_{\mathrm {st}}\otimes _{L_0}L$
an action of
![]() $\varphi _q$
and the monodromy operator N satisfying
$\varphi _q$
and the monodromy operator N satisfying
![]() $N\varphi _q = q\varphi _qN.$
$N\varphi _q = q\varphi _qN.$
We now explain how to modify this action in order to obtain an
![]() $L^{nr}$
-linear representation of the Weil group
$L^{nr}$
-linear representation of the Weil group
![]() $W_L.$
By local class field theory the maximal abelian extension
$W_L.$
By local class field theory the maximal abelian extension
![]() $L^{ab}$
of L is given by the composite
$L^{ab}$
of L is given by the composite
![]() $L^{nr}L_\infty $
and
$L^{nr}L_\infty $
and
![]() $L^{nr}\cap L_\infty =L.$
Consider the reciprocity map
$L^{nr}\cap L_\infty =L.$
Consider the reciprocity map
which by our convention sends
![]() $\pi _L$
to the geometric Frobenius on
$\pi _L$
to the geometric Frobenius on
![]() $L^{nr}.$
This induces an isomorphism
$L^{nr}.$
This induces an isomorphism
![]() $L^{\times } \cong W_L^{ab} \cong \varphi _L^{\mathbb {Z}} \times \Gamma _L.$
We denote by
$L^{\times } \cong W_L^{ab} \cong \varphi _L^{\mathbb {Z}} \times \Gamma _L.$
We denote by
![]() $\bar {\phantom {m}}:W_L\twoheadrightarrow W_L^{ab}$
the canonical surjection and define a linearised action of
$\bar {\phantom {m}}:W_L\twoheadrightarrow W_L^{ab}$
the canonical surjection and define a linearised action of
![]() $W_L$
on
$W_L$
on
![]() $D_{pst}(M)$
by setting
$D_{pst}(M)$
by setting
where
![]() $\rho _{semi-lin}$
denotes the action we considered previously. For
$\rho _{semi-lin}$
denotes the action we considered previously. For
![]() $a \in L^{nr}$
, we then have
$a \in L^{nr}$
, we then have
 $$ \begin{align*}\rho_{lin}(g)(ax) &= \varphi_q^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}\big(\rho_{semi-lin}(g)(ax)\big)\\ &=\varphi_q^{v_\pi((\operatorname{rec}^{-1}(\bar{g}))}\big(\rho_{semi-lin}(g)(a)\rho_{semi-lin}(g)(x)\big)\\ &= \varphi_q^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}\big((\varphi_L^{-1})^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}(a)\big)\cdot \varphi_q^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}\big(\rho_{semi-lin}(g)(x)\big)\\ &= a \rho_{lin}(g)(x). \end{align*} $$
$$ \begin{align*}\rho_{lin}(g)(ax) &= \varphi_q^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}\big(\rho_{semi-lin}(g)(ax)\big)\\ &=\varphi_q^{v_\pi((\operatorname{rec}^{-1}(\bar{g}))}\big(\rho_{semi-lin}(g)(a)\rho_{semi-lin}(g)(x)\big)\\ &= \varphi_q^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}\big((\varphi_L^{-1})^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}(a)\big)\cdot \varphi_q^{v_\pi(\operatorname{rec}^{-1}(\bar{g}))}\big(\rho_{semi-lin}(g)(x)\big)\\ &= a \rho_{lin}(g)(x). \end{align*} $$
By passing to the base change
![]() $D_{pst}(M)\otimes _LL_{\infty }$
(with trivial action on
$D_{pst}(M)\otimes _LL_{\infty }$
(with trivial action on
![]() $L_\infty $
) we are finally able to define
$L_\infty $
) we are finally able to define
![]() $W(M):= (D_{pst}(M)\otimes _LL_{\infty }, \rho _{lin}, N)$
which is an
$W(M):= (D_{pst}(M)\otimes _LL_{\infty }, \rho _{lin}, N)$
which is an
![]() $L^{ab}$
-linear Weil-Deligne representation (Note that since
$L^{ab}$
-linear Weil-Deligne representation (Note that since
![]() $D_{pst}(M)$
can be written as a base extension of some
$D_{pst}(M)$
can be written as a base extension of some
![]() $D_{st}(M_{\mid F})$
, the action of the inertia group
$D_{st}(M_{\mid F})$
, the action of the inertia group
![]() $I_F$
is discrete and because
$I_F$
is discrete and because
![]() $I_F$
is open in
$I_F$
is open in
![]() $W_L$
the action of
$W_L$
the action of
![]() $W_L$
is discrete.)
$W_L$
is discrete.)
Example 7.9. The linearized Weil-Deligne representation
![]() $W:=W(\mathcal {R}_K(\delta ))$
with
$W:=W(\mathcal {R}_K(\delta ))$
with
![]() $\delta =\delta _{\mathrm {lc}}x^k $
is given by the character
$\delta =\delta _{\mathrm {lc}}x^k $
is given by the character
![]() $ \delta _W= \delta _{\mathrm {lc}} \delta ^{un}_{\pi _L^{-k}}:L^\times \to (L^{ab})^\times $
via class field theory sending
$ \delta _W= \delta _{\mathrm {lc}} \delta ^{un}_{\pi _L^{-k}}:L^\times \to (L^{ab})^\times $
via class field theory sending
![]() $\pi _L$
to the geometric Frobenius. In particular,
$\pi _L$
to the geometric Frobenius. In particular,
Proof. For the convenience of the reader we give a proof using B-pairs. Let
![]() $\mathbf {e}_{\delta }$
be the obvious basis of
$\mathbf {e}_{\delta }$
be the obvious basis of
![]() $\mathcal {R}_L(\delta )$
and write
$\mathcal {R}_L(\delta )$
and write
![]() $\delta (\pi ) = \delta _{lc}(\pi ) \pi ^k =\pi ^l\alpha $
with
$\delta (\pi ) = \delta _{lc}(\pi ) \pi ^k =\pi ^l\alpha $
with
![]() $\alpha \in o_L^\times .$
We can find
$\alpha \in o_L^\times .$
We can find
![]() $a \in L^{nr} \subset \tilde {\mathcal {R}}$
such that
$a \in L^{nr} \subset \tilde {\mathcal {R}}$
such that
![]() $\varphi _q(a) = \alpha a$
and hence
$\varphi _q(a) = \alpha a$
and hence
![]() $y:=\frac {1}{a t_{LT}^l}\otimes \mathbf {e}_{\delta } \in W_e(\mathcal {R}_L(\delta )) = (\tilde {\mathcal {R}}[1/t_{LT}] \otimes _{\mathcal {R}} \mathcal {R}_L(\delta ))^{\varphi _L=1}.$
Note that
$y:=\frac {1}{a t_{LT}^l}\otimes \mathbf {e}_{\delta } \in W_e(\mathcal {R}_L(\delta )) = (\tilde {\mathcal {R}}[1/t_{LT}] \otimes _{\mathcal {R}} \mathcal {R}_L(\delta ))^{\varphi _L=1}.$
Note that
![]() $G_L$
acts diagonally on
$G_L$
acts diagonally on
![]() $W_e(\mathcal {R}_L(\delta )),$
where the action on
$W_e(\mathcal {R}_L(\delta )),$
where the action on
![]() $\mathcal {R}_L(\delta )$
is given via the quotient
$\mathcal {R}_L(\delta )$
is given via the quotient
![]() $\Gamma _L.$
Let F be a field extension of L such that
$\Gamma _L.$
Let F be a field extension of L such that
![]() $\delta _{lc}$
is trivial when restricted to the image of
$\delta _{lc}$
is trivial when restricted to the image of
![]() $G_F$
in
$G_F$
in
![]() $\Gamma _L.$
Then the action of
$\Gamma _L.$
Then the action of
![]() $g \in G_F$
is given by
$g \in G_F$
is given by
![]() $g(y) = a/g(a) \chi _{LT}(g)^{k-l}y$
and hence
$g(y) = a/g(a) \chi _{LT}(g)^{k-l}y$
and hence
![]() $z:= t_{LT}^{l-k}a \otimes y$
is a basis of
$z:= t_{LT}^{l-k}a \otimes y$
is a basis of
![]() $(B_{st}\otimes W_e(\mathcal {R}_L(\delta )))^{G_F}.$
Write
$(B_{st}\otimes W_e(\mathcal {R}_L(\delta )))^{G_F}.$
Write
![]() $\delta = x^k \delta ^{un}_{\pi _L^{l-k}} \delta ^{un}_{\alpha } \rho $
where
$\delta = x^k \delta ^{un}_{\pi _L^{l-k}} \delta ^{un}_{\alpha } \rho $
where
![]() $\rho $
is a locally constant character with
$\rho $
is a locally constant character with
![]() $\rho (\pi )=1$
and
$\rho (\pi )=1$
and
![]() $\rho (\gamma ) = \delta _{lc}(\gamma )$
for
$\rho (\gamma ) = \delta _{lc}(\gamma )$
for
![]() $\gamma \in \Gamma _L.$
In this representation it is clear that the residual (non-linearised) action of
$\gamma \in \Gamma _L.$
In this representation it is clear that the residual (non-linearised) action of
![]() $G_L$
is given by
$G_L$
is given by
![]() $gz = \rho (g)z$
and hence the linearised action is given by
$gz = \rho (g)z$
and hence the linearised action is given by
 $$ \begin{align*} \rho(g)\varphi_q^{v_\pi(\operatorname{rec}^{-1}g)}(z)& = (\pi^{l-k}\alpha)^{v_\pi(\operatorname{rec}^{-1}g)}\rho(g)z \\ & = \delta_{lc}(\pi)^{v_\pi(\operatorname{rec}^{-1}g)} (\pi^{-k})^{v_\pi(\operatorname{rec}^{-1}g)}\rho(g) = \delta_{lc} \delta^{un}_{\pi^{-k}}(g)z.\\[-36pt] \end{align*} $$
$$ \begin{align*} \rho(g)\varphi_q^{v_\pi(\operatorname{rec}^{-1}g)}(z)& = (\pi^{l-k}\alpha)^{v_\pi(\operatorname{rec}^{-1}g)}\rho(g)z \\ & = \delta_{lc}(\pi)^{v_\pi(\operatorname{rec}^{-1}g)} (\pi^{-k})^{v_\pi(\operatorname{rec}^{-1}g)}\rho(g) = \delta_{lc} \delta^{un}_{\pi^{-k}}(g)z.\\[-36pt] \end{align*} $$
7.4.1 Equivariant de Rham epsilon constants
For a de Rham
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_L$
we would like to define the epsilon constant of M to be the
$\mathcal {R}_L$
we would like to define the epsilon constant of M to be the
![]() $\varepsilon $
-constant associated to
$\varepsilon $
-constant associated to
![]() $W(M)$
$W(M)$
defined in section 6 using the adjustment (58). In the cyclotomic case (take for simplicity
![]() $L = K = \mathbb {Q}_p$
), these
$L = K = \mathbb {Q}_p$
), these
![]() $\varepsilon $
-constants can be viewed as elements of
$\varepsilon $
-constants can be viewed as elements of
![]() $L_n = \mathbb {Q}_p(\zeta _{p^n}).$
In our case the constants are defined using p-power roots of unity which are “built” from the LT-torsion points using the power series
$L_n = \mathbb {Q}_p(\zeta _{p^n}).$
In our case the constants are defined using p-power roots of unity which are “built” from the LT-torsion points using the power series
![]() $\eta (-,T).$
The problem we run into is that, contrary to the classical case, we can not assume that
$\eta (-,T).$
The problem we run into is that, contrary to the classical case, we can not assume that
![]() $L_n$
contains the p-power roots of unity.
$L_n$
contains the p-power roots of unity.
Suppose K contains
![]() $L^{ab}.$
Then it makes sense to view
$L^{ab}.$
Then it makes sense to view
![]() $\varepsilon (M,\psi ,dx)$
as an element of
$\varepsilon (M,\psi ,dx)$
as an element of
![]() $K,$
but by our convention that K carries the trivial
$K,$
but by our convention that K carries the trivial
![]() $\Gamma _L$
-action, we do not have
$\Gamma _L$
-action, we do not have
![]() $\gamma (\varepsilon (M,\psi _u,dx)) = \varepsilon (M,\psi _{\gamma (u)},dx),$
which we will need for technical reasons below in (67),in the form of Remark 7.11. Roughly speaking we would like to define the
$\gamma (\varepsilon (M,\psi _u,dx)) = \varepsilon (M,\psi _{\gamma (u)},dx),$
which we will need for technical reasons below in (67),in the form of Remark 7.11. Roughly speaking we would like to define the
![]() $\varepsilon $
-constants as elements of
$\varepsilon $
-constants as elements of
![]() $L_n\otimes _L K$
with n large enough, such that the definition of the epsilon constants “involves only” the
$L_n\otimes _L K$
with n large enough, such that the definition of the epsilon constants “involves only” the
![]() $\pi _L^n$
-division points of the Lubin-Tate group. We make this concept precise via the following equivariant construction.
$\pi _L^n$
-division points of the Lubin-Tate group. We make this concept precise via the following equivariant construction.
Definition 7.10. Suppose the complete subfield K of
![]() $\mathbb {C}_p$
contains
$\mathbb {C}_p$
contains
![]() $L^{ab}$
and let W be a Weil-Deligne representation of
$L^{ab}$
and let W be a Weil-Deligne representation of
![]() $W_L$
with coefficients in
$W_L$
with coefficients in
![]() $K.$
Building on the
$K.$
Building on the
![]() $\varepsilon $
-constants defined in section 6 with
$\varepsilon $
-constants defined in section 6 with
![]() $E=K$
we define the
$E=K$
we define the
![]() $\Gamma _L$
-equivariant
$\Gamma _L$
-equivariant
![]() $\varepsilon $
-constant
$\varepsilon $
-constant
for lifts
![]() $\hat {\tau }$
of
$\hat {\tau }$
of
![]() $\tau $
to
$\tau $
to
![]() $\Gamma _L$
, viewed as an element ofFootnote
21
$\Gamma _L$
, viewed as an element ofFootnote
21
via the canonical isomorphism, where
![]() $n \gg 0$
is large enough such that the
$n \gg 0$
is large enough such that the
![]() $\varepsilon $
-constant can be defined in terms of characters of conductor
$\varepsilon $
-constant can be defined in terms of characters of conductor
![]() $\leq n$
according to Deligne’s (inductive) construction principle: In the rank one case, i.e., in the case of a locally constant character
$\leq n$
according to Deligne’s (inductive) construction principle: In the rank one case, i.e., in the case of a locally constant character
![]() $\delta \colon L^\times \to K^\times $
, one can take
$\delta \colon L^\times \to K^\times $
, one can take
![]() $n \geq a(\delta ).$
In general, the definition of the
$n \geq a(\delta ).$
In general, the definition of the
![]() $\varepsilon $
-constant involves multiple such characters defined over finite extensions of L (cf. [Reference Deligne18, p. 536, Equation 4.2.1]) and one has to choose n greater than the supremum of all appearing conductors.
$\varepsilon $
-constant involves multiple such characters defined over finite extensions of L (cf. [Reference Deligne18, p. 536, Equation 4.2.1]) and one has to choose n greater than the supremum of all appearing conductors.
Remark 7.11. The
![]() $\varepsilon $
-constant
$\varepsilon $
-constant
![]() $\tilde {\varepsilon }(W,u,dx)$
is well-defined, i.e. its definition above is independent of the choices of the lifts
$\tilde {\varepsilon }(W,u,dx)$
is well-defined, i.e. its definition above is independent of the choices of the lifts
![]() $\hat {\tau }$
. Furthermore, with respect to the
$\hat {\tau }$
. Furthermore, with respect to the
![]() $\Gamma _L$
-action on
$\Gamma _L$
-action on
![]() $L_n \otimes _LK$
via the left tensor factor we have
$L_n \otimes _LK$
via the left tensor factor we have
Proof. Without loss of generality we can assume W is of rank one corresponding to a locally constant character
![]() $\delta \colon L^\times \to K^\times $
due to Deligne’s construction principle. First of all we note that
$\delta \colon L^\times \to K^\times $
due to Deligne’s construction principle. First of all we note that
![]() $\tilde {\varepsilon }$
is well-defined since
$\tilde {\varepsilon }$
is well-defined since
![]() $ u_{a(\delta )} \in L_n$
by assumption. Because the natural isomorphism
$ u_{a(\delta )} \in L_n$
by assumption. Because the natural isomorphism
![]() $L_n \otimes _L K \cong \prod _{\tau \colon L_n \to K}K$
maps
$L_n \otimes _L K \cong \prod _{\tau \colon L_n \to K}K$
maps
![]() $u \otimes 1$
to
$u \otimes 1$
to
![]() $(\tau (u))_\tau ,$
we can see that
$(\tau (u))_\tau ,$
we can see that
![]() $\tilde {\varepsilon }$
is obtained by replacing in (57) the elements
$\tilde {\varepsilon }$
is obtained by replacing in (57) the elements
![]() $\eta (a,u_{a(\delta )})$
by the series
$\eta (a,u_{a(\delta )})$
by the series
![]() $\eta (a,T)$
evaluated at the element
$\eta (a,T)$
evaluated at the element
![]() $(u_{a(\delta )} \otimes 1)$
, i.e., by
$(u_{a(\delta )} \otimes 1)$
, i.e., by
![]() $\sum _{i \in \mathbb {N}_0} (1 \otimes a_i) (u_{a(\delta )} \otimes 1)^i,$
where
$\sum _{i \in \mathbb {N}_0} (1 \otimes a_i) (u_{a(\delta )} \otimes 1)^i,$
where
![]() $\eta (a,T) = \sum a_iT^i$
(this expression converges with respect to the tensor product topology). The formula for the
$\eta (a,T) = \sum a_iT^i$
(this expression converges with respect to the tensor product topology). The formula for the
![]() $\gamma $
-action can be read off from (57).
$\gamma $
-action can be read off from (57).
Definition 7.12. For a de Rham
![]() $(\varphi _L,\Gamma _L)$
-module M over
$(\varphi _L,\Gamma _L)$
-module M over
![]() $\mathcal {R}_L$
we define the epsilon constant of M to be the
$\mathcal {R}_L$
we define the epsilon constant of M to be the
![]() $\Gamma _L$
-equivariant
$\Gamma _L$
-equivariant
![]() $\varepsilon $
-constant associated to
$\varepsilon $
-constant associated to
![]() $W(M)$
$W(M)$
We usually omit
![]() $dx$
from the notation and write
$dx$
from the notation and write
Remark 7.13. Let
![]() $dx$
be the self dual Haar measure with respect to
$dx$
be the self dual Haar measure with respect to
![]() $\psi _u,$
then
$\psi _u,$
then
Proof. In order to apply (60) we check that we have an isomorphism
![]() $\mathbf {D}_{\mathrm {pst}}(\tilde {M})\cong \mathbf {D}_{\mathrm {pst}}({M})^*(|x|)$
. Using the usual functorialities it suffices to check that
$\mathbf {D}_{\mathrm {pst}}(\tilde {M})\cong \mathbf {D}_{\mathrm {pst}}({M})^*(|x|)$
. Using the usual functorialities it suffices to check that
![]() $\mathbf {D}_{\mathrm {pst}}(\Omega ^1)\cong L^{nr}(|x|)$
, which is a special case of Example 7.9. The proof of the other required equation
$\mathbf {D}_{\mathrm {pst}}(\Omega ^1)\cong L^{nr}(|x|)$
, which is a special case of Example 7.9. The proof of the other required equation
is then also standard, see e.g. [Reference Damrich17, claim 5 in proof of Prop. 2.2.20].
We now describe how our construction relates to the étale and the cyclotomic case. The comparison of
![]() $\varepsilon $
-constants involves a number of choices and we will only give an informal comparison of the constructions presented here and the ones from [Reference Nakamura36] - by which we mean that we give a comparison up to constants that only depend on
$\varepsilon $
-constants involves a number of choices and we will only give an informal comparison of the constructions presented here and the ones from [Reference Nakamura36] - by which we mean that we give a comparison up to constants that only depend on
![]() $L/\mathbb {Q}_p.$
There are two avenues to be considered. On the one hand, we can specialise our constructions to the cyclotomic case
$L/\mathbb {Q}_p.$
There are two avenues to be considered. On the one hand, we can specialise our constructions to the cyclotomic case
![]() $L=\mathbb {Q}_p,$
taking
$L=\mathbb {Q}_p,$
taking
![]() $u_n = \zeta _{p^n}-1$
and
$u_n = \zeta _{p^n}-1$
and
![]() $\Omega =1.$
Because
$\Omega =1.$
Because
![]() $\zeta _{p^n} = 1+ u_n = \eta (1,(u_n))$
in this case our construction specialises to Nakamura’s, more precisely, our
$\zeta _{p^n} = 1+ u_n = \eta (1,(u_n))$
in this case our construction specialises to Nakamura’s, more precisely, our
![]() $\tilde {\varepsilon }$
is equal to
$\tilde {\varepsilon }$
is equal to
![]() $\varepsilon _{\text {Na}} \otimes 1$
viewed as an element of
$\varepsilon _{\text {Na}} \otimes 1$
viewed as an element of
![]() $L_\infty \otimes _{\mathbb {Q}_p} K,$
where
$L_\infty \otimes _{\mathbb {Q}_p} K,$
where
![]() $\varepsilon _{Na}$
denotes the constant from [Reference Nakamura36, Section 3C]. Indeed the elements
$\varepsilon _{Na}$
denotes the constant from [Reference Nakamura36, Section 3C]. Indeed the elements
![]() $\eta (a,u_n \otimes 1) = \zeta ^a_{p^n} \otimes 1$
appearing in 7.11 lie inside
$\eta (a,u_n \otimes 1) = \zeta ^a_{p^n} \otimes 1$
appearing in 7.11 lie inside
![]() $L_n \otimes _{\mathbb {Q}_p} \mathbb {Q}_p.$
$L_n \otimes _{\mathbb {Q}_p} \mathbb {Q}_p.$
On the other hand, we take the induction of an L-linear
![]() $G_L$
-representation V and treat it as an L-linear representation of
$G_L$
-representation V and treat it as an L-linear representation of
![]() $G_{\mathbb {Q}_p}$
. For the moment let us assume
$G_{\mathbb {Q}_p}$
. For the moment let us assume
![]() $V \in \operatorname {Rep}_L{G_L}$
is semi-stable and L-analytic and set
$V \in \operatorname {Rep}_L{G_L}$
is semi-stable and L-analytic and set
![]() $X:= \operatorname {Ind}_{L/\mathbb {Q}_p}V.$
Let
$X:= \operatorname {Ind}_{L/\mathbb {Q}_p}V.$
Let
![]() $\mathbb {Q}_p\subseteq L_0 \subseteq L$
be the maximal unramified subextension. We can decompose
$\mathbb {Q}_p\subseteq L_0 \subseteq L$
be the maximal unramified subextension. We can decompose
 $$ \begin{align*}(\mathbf{B}_{st}\otimes_{\mathbb{Q}_p}V)^{G_L} \cong \prod_{\tau\colon L_0 \to \overline{\mathbb{Q}_p}}(\mathbf{B}_{st}\otimes_{L_0,\tau}V)^{G_L}\end{align*} $$
$$ \begin{align*}(\mathbf{B}_{st}\otimes_{\mathbb{Q}_p}V)^{G_L} \cong \prod_{\tau\colon L_0 \to \overline{\mathbb{Q}_p}}(\mathbf{B}_{st}\otimes_{L_0,\tau}V)^{G_L}\end{align*} $$
and have a similar decomposition for
![]() $(\mathbf {B}_{st} \otimes _{\mathbb {Q}_p} X)^{G_{\mathbb {Q}_p}}.$
The epsilon constants of the induction (given suitable choices of additive characters) are related by explicit constants independent of V (see (59)). Ignoring these, the
$(\mathbf {B}_{st} \otimes _{\mathbb {Q}_p} X)^{G_{\mathbb {Q}_p}}.$
The epsilon constants of the induction (given suitable choices of additive characters) are related by explicit constants independent of V (see (59)). Ignoring these, the
![]() $\varepsilon $
-constants defined by Nakamura are the product of the
$\varepsilon $
-constants defined by Nakamura are the product of the
![]() $\varepsilon $
-constants of each component in the sense that he attaches to X a tuple
$\varepsilon $
-constants of each component in the sense that he attaches to X a tuple
![]() $(W_\tau )_\tau $
of
$(W_\tau )_\tau $
of
![]() $W_{\mathbb {Q}_p}$
-representations to which he attaches a tuple
$W_{\mathbb {Q}_p}$
-representations to which he attaches a tuple
![]() $(\varepsilon (W_\tau ))_\tau $
(cf. [Reference Nakamura36, p.359] for details) of constants living over
$(\varepsilon (W_\tau ))_\tau $
(cf. [Reference Nakamura36, p.359] for details) of constants living over
![]() $\mathbb {Q}_{p}(\zeta _{p^{\infty }})\otimes _{\mathbb {Q}_p}L$
. In contrast we attach (informally speaking) to the
$\mathbb {Q}_{p}(\zeta _{p^{\infty }})\otimes _{\mathbb {Q}_p}L$
. In contrast we attach (informally speaking) to the
![]() $\tau =\operatorname {id}$
component a constant
$\tau =\operatorname {id}$
component a constant
![]() $\varepsilon (W_{id}).$
As we can not assume that
$\varepsilon (W_{id}).$
As we can not assume that
![]() $L_\infty $
contains the p-th roots of unity, an analogous construction involving
$L_\infty $
contains the p-th roots of unity, an analogous construction involving
![]() $L_\infty $
does not work in the obvious sense and taking the base change to
$L_\infty $
does not work in the obvious sense and taking the base change to
![]() $L^{ab}$
with
$L^{ab}$
with
![]() $G_{L}$
acting naturally on
$G_{L}$
acting naturally on
![]() $L^{ab}$
does not provide us with the Galois action needed to make the constructions in 7.11 work. By assuming
$L^{ab}$
does not provide us with the Galois action needed to make the constructions in 7.11 work. By assuming
![]() $L^{ab} \subset K$
we can make sense of the elements
$L^{ab} \subset K$
we can make sense of the elements
![]() $\eta (a,(u_n \otimes 1)) \in L_n \otimes _LK,$
which allow us to define
$\eta (a,(u_n \otimes 1)) \in L_n \otimes _LK,$
which allow us to define
![]() $\tilde {\varepsilon }(W_{id})$
with the desired technical properties now living over
$\tilde {\varepsilon }(W_{id})$
with the desired technical properties now living over
![]() $L_n \otimes _LK= \prod _{\sigma \in \operatorname {Hom}_L(L_n,K)} K$
for
$L_n \otimes _LK= \prod _{\sigma \in \operatorname {Hom}_L(L_n,K)} K$
for
![]() $n \gg 0$
(note that the index set of the product is different in comparison to Nakamura’s situation). By projecting to the
$n \gg 0$
(note that the index set of the product is different in comparison to Nakamura’s situation). By projecting to the
![]() $\sigma = \operatorname {id}$
component we can recover Nakamura’s
$\sigma = \operatorname {id}$
component we can recover Nakamura’s
![]() $\varepsilon (W_{\operatorname {id}})$
and our constant
$\varepsilon (W_{\operatorname {id}})$
and our constant
![]() $\tilde {\varepsilon (W_{\operatorname {id}})}=(\varepsilon (W_{\operatorname {id}},\psi _{\hat {\sigma }(u)},dx))_\sigma $
should be informally thought of as
$\tilde {\varepsilon (W_{\operatorname {id}})}=(\varepsilon (W_{\operatorname {id}},\psi _{\hat {\sigma }(u)},dx))_\sigma $
should be informally thought of as
![]() $(\sigma (\varepsilon (W_{\operatorname {id}})))_{\sigma }$
, which is not well-defined as
$(\sigma (\varepsilon (W_{\operatorname {id}})))_{\sigma }$
, which is not well-defined as
![]() $\sigma $
does not act on K but only on
$\sigma $
does not act on K but only on
![]() $L_n.$
$L_n.$
The fact that V is semi-stable and L-analytic forces each non-identity component to be potentially unramified (since they are semi-stable with Hodge-Tate weights
![]() $0$
). If they are even unramified, all
$0$
). If they are even unramified, all
![]() $\varepsilon $
-constants at non-identity components would be
$\varepsilon $
-constants at non-identity components would be
![]() $1$
and both methods give comparable
$1$
and both methods give comparable
![]() $\varepsilon $
-constants (more precisely, at
$\varepsilon $
-constants (more precisely, at
![]() $\sigma =\operatorname {id}$
they would be the same up to explicit constants independent of V). If the action on the non-identity components is only potentially unramified, we cannot assume that the
$\sigma =\operatorname {id}$
they would be the same up to explicit constants independent of V). If the action on the non-identity components is only potentially unramified, we cannot assume that the
![]() $\varepsilon $
-constants at the non-identity embeddings are
$\varepsilon $
-constants at the non-identity embeddings are
![]() $1.$
In particular these embeddings contribute to the
$1.$
In particular these embeddings contribute to the
![]() $\varepsilon $
-constant attached to V by Nakamura in a way that can not be captured by only considering the identity embedding.
$\varepsilon $
-constant attached to V by Nakamura in a way that can not be captured by only considering the identity embedding.
7.4.2 The de Rham epsilon-isomorphism
For each de Rham
![]() $(\varphi ,\Gamma _L)$
-module M over
$(\varphi ,\Gamma _L)$
-module M over
![]() $\mathcal {R}_K$
which arises as a base change of a
$\mathcal {R}_K$
which arises as a base change of a
![]() $(\varphi _L,\Gamma _L)$
-module
$(\varphi _L,\Gamma _L)$
-module
![]() $M_0$
over
$M_0$
over
![]() $\mathcal {R}_F$
for some finite extension
$\mathcal {R}_F$
for some finite extension
![]() $F/L$
, and for each generator u of
$F/L$
, and for each generator u of
![]() $T_{\pi }$
we are going to define a trivialization
$T_{\pi }$
we are going to define a trivialization
as product of three terms
where
 $$ \begin{align*} \Theta(M)\colon & \mathbf{1}\xrightarrow{\cong} \Delta_{K,1}(M)\mathbf{d}_K( \mathbf{D}_{\text{dR}}(M) ),\\ \Theta_{dR,u}(M_0)\colon & \mathbf{d}_K( \mathbf{D}_{\text{dR}}(M) ) \xrightarrow{\cong}\Delta_{K,2}(M),\\ \Gamma(M) & \in K^\times. \end{align*} $$
$$ \begin{align*} \Theta(M)\colon & \mathbf{1}\xrightarrow{\cong} \Delta_{K,1}(M)\mathbf{d}_K( \mathbf{D}_{\text{dR}}(M) ),\\ \Theta_{dR,u}(M_0)\colon & \mathbf{d}_K( \mathbf{D}_{\text{dR}}(M) ) \xrightarrow{\cong}\Delta_{K,2}(M),\\ \Gamma(M) & \in K^\times. \end{align*} $$
To keep notation light and consistent with the previous subsection we will, without loss of generality, restrict ourselves to the case
![]() $L=F.$
Firstly, we define
$L=F.$
Firstly, we define
![]() $\Gamma (M)$
, which depends only on the Hodge–Tate weights of M. For
$\Gamma (M)$
, which depends only on the Hodge–Tate weights of M. For
![]() $r \in \mathbb {Z}$
let
$r \in \mathbb {Z}$
let
so
![]() $n(r)$
is the multiplicity of r as a Hodge–Tate weight of M. We adopt the convention in this paper that the Hodge–Tate weight of the cyclotomic character is
$n(r)$
is the multiplicity of r as a Hodge–Tate weight of M. We adopt the convention in this paper that the Hodge–Tate weight of the cyclotomic character is
![]() $1$
. We define
$1$
. We define
 $$\begin{align*}\Gamma^*(r) := \begin{cases} (r-1)! & \text{if } r> 0,\\ \frac{(-1)^r}{(-r)!} & \text{if } r \le 0,\end{cases}\end{align*}$$
$$\begin{align*}\Gamma^*(r) := \begin{cases} (r-1)! & \text{if } r> 0,\\ \frac{(-1)^r}{(-r)!} & \text{if } r \le 0,\end{cases}\end{align*}$$
the leading coefficient of the Taylor series of
![]() $\Gamma (s)$
at
$\Gamma (s)$
at
![]() $s = r$
. Then we set
$s = r$
. Then we set
Secondly,
![]() $\Theta (M)$
is obtained by applying the determinant functor to the following exact sequence
$\Theta (M)$
is obtained by applying the determinant functor to the following exact sequence

which arises from joining the bottom exact sequence of (46) with the dual of the same sequence applied to
![]() $\tilde {M}$
by local duality
$\tilde {M}$
by local duality
![]() $\langle -,-\rangle _{{M}}$
in 5.18 and using Remark 5.13, upon
$\langle -,-\rangle _{{M}}$
in 5.18 and using Remark 5.13, upon
-
(i) using the tautological exact sequence

 as well as de Rham duality in the form and
as well as de Rham duality in the form and $$\begin{align*}\mathbf{D}^{}_{\text{dR}}({M})^0\xrightarrow{\cong} t_{\tilde{M}}^*, \; x\mapsto\{\bar{y}\mapsto [y,x]_{dR,\tilde{M}}\},\end{align*}$$
$$\begin{align*}\mathbf{D}^{}_{\text{dR}}({M})^0\xrightarrow{\cong} t_{\tilde{M}}^*, \; x\mapsto\{\bar{y}\mapsto [y,x]_{dR,\tilde{M}}\},\end{align*}$$
-
(ii) identifying each time the two instances of
 $\mathbf {D}^{}_{\text {cris}}(\tilde {M})^*$
and
$\mathbf {D}^{}_{\text {cris}}(\tilde {M})^*$
and
 $\mathbf {D}^{}_{\text {cris}}({M})$
, respectively, by the identity.
$\mathbf {D}^{}_{\text {cris}}({M})$
, respectively, by the identity.
Thirdly - here comes the reason why we use a model
![]() $M_0$
-
$M_0$
-
![]() $\Theta _{dR,u}(M_0):=f_{M_0,u}^{-1}$
is defined by the analogue of [Reference Nakamura36, Lem. 3.4] which - using Remark 7.11 and (64) - induces an isomorphism
$\Theta _{dR,u}(M_0):=f_{M_0,u}^{-1}$
is defined by the analogue of [Reference Nakamura36, Lem. 3.4] which - using Remark 7.11 and (64) - induces an isomorphism
![]() $f_{M_0,u}:\Delta _{K,2}(M)\xrightarrow {\cong } d_K( \mathbf {D}^{}_{\text {dR}}({M}))$
from the map (taking into account Remark 3.21)
$f_{M_0,u}:\Delta _{K,2}(M)\xrightarrow {\cong } d_K( \mathbf {D}^{}_{\text {dR}}({M}))$
from the map (taking into account Remark 3.21)
 $$ \begin{align} \mathcal{L}_K(M) \to \mathbf{D}^{}_{\text{dif},n}(\mathrm{det}_{\mathcal{R}_K}M)=\ &K_n((t_{LT}))\otimes_{\iota_n,\mathcal{R}_K^{(n)}}(\mathrm{det}_{\mathcal{R}_K}M)^{(n)} \\ \notag & x\mapsto \big(\tilde{\varepsilon}(M_0,u)^{-1} \cdot \frac{1}{t_{LT}^{h_M}}\big) \otimes \varphi^n(x) \end{align} $$
$$ \begin{align} \mathcal{L}_K(M) \to \mathbf{D}^{}_{\text{dif},n}(\mathrm{det}_{\mathcal{R}_K}M)=\ &K_n((t_{LT}))\otimes_{\iota_n,\mathcal{R}_K^{(n)}}(\mathrm{det}_{\mathcal{R}_K}M)^{(n)} \\ \notag & x\mapsto \big(\tilde{\varepsilon}(M_0,u)^{-1} \cdot \frac{1}{t_{LT}^{h_M}}\big) \otimes \varphi^n(x) \end{align} $$
for sufficiently large n such that the equivariant constant
![]() $\tilde {\varepsilon }(W(M_0),u,dx)$
from Definition 7.10 lies in
$\tilde {\varepsilon }(W(M_0),u,dx)$
from Definition 7.10 lies in
![]() $L_n \otimes K\subseteq K_n((t_{LT}))$
, where
$L_n \otimes K\subseteq K_n((t_{LT}))$
, where
![]() $h_M$
denotes the Hodge-Tate weight of
$h_M$
denotes the Hodge-Tate weight of
![]() $\det M.$
One easily checks independence of the choice of a model
$\det M.$
One easily checks independence of the choice of a model
![]() $M_0$
- the reason why we use
$M_0$
- the reason why we use
![]() $M_0$
in the notation is to indicate that we need a model to define these objects. Note that (67) depends on u in two ways. On the one hand via
$M_0$
in the notation is to indicate that we need a model to define these objects. Note that (67) depends on u in two ways. On the one hand via
![]() $\tilde {\varepsilon }$
and on the other hand due to the explicit appearance of
$\tilde {\varepsilon }$
and on the other hand due to the explicit appearance of
![]() $t_{LT}$
which, as pointed out in 3.11, depends on the choice of
$t_{LT}$
which, as pointed out in 3.11, depends on the choice of
![]() $u.$
An analogous computation to [Reference Nakamura36, Remark 3.5] shows that
$u.$
An analogous computation to [Reference Nakamura36, Remark 3.5] shows that
![]() $f_{M_0,au} = \delta _{\det _{\mathcal {R}_K}M}(a)^{-1} f_{M_0,u}$
for
$f_{M_0,au} = \delta _{\det _{\mathcal {R}_K}M}(a)^{-1} f_{M_0,u}$
for
![]() $a \in o_L^\times .$
$a \in o_L^\times .$
Proposition 7.14 (Properties (ii) and (iv) for
 $ \varepsilon ^{dR}_{L,u}(M_0)$
)
$ \varepsilon ^{dR}_{L,u}(M_0)$
)
-
(i) For any exact sequence
 , we have under the canonical isomorphism
, we have under the canonical isomorphism $$\begin{align*}\varepsilon^{dR}_{L,u}(M_{2,0})=\varepsilon^{dR}_{L,u}(M_{1,0})\otimes\varepsilon^{dR}_{L,u}(M_{3,0})\end{align*}$$
$$\begin{align*}\varepsilon^{dR}_{L,u}(M_{2,0})=\varepsilon^{dR}_{L,u}(M_{1,0})\otimes\varepsilon^{dR}_{L,u}(M_{3,0})\end{align*}$$
 $\Delta _K(M_2)\cong \Delta _K(M_1)\otimes \Delta _K(M_3).$
$\Delta _K(M_2)\cong \Delta _K(M_1)\otimes \Delta _K(M_3).$
-
(ii) The following diagram of isomorphisms commutes
where
 $h(\chi ^r):(K(\chi ^r),0)\to \mathbf {1}_K$
sends
$h(\chi ^r):(K(\chi ^r),0)\to \mathbf {1}_K$
sends
 $\mathbf {e}_r$
to
$\mathbf {e}_r$
to
 $1.$
$1.$
Proof. Analogous to [Reference Nakamura36, Lem. 3.7], but with some differences. Due to the period
![]() $\Omega $
in the definition of
$\Omega $
in the definition of
![]() $\Gamma (M)$
we now obtain
$\Gamma (M)$
we now obtain
instead of (27) in (loc. cit.). By definition, the second part of the long exact sequence (66) for
![]() $\tilde {M}$
is given by the commutativity of the following diagram with exact rows
$\tilde {M}$
is given by the commutativity of the following diagram with exact rows

where we have identified
![]() $M\cong \tilde {\tilde {M}}$
and abbreviated
$M\cong \tilde {\tilde {M}}$
and abbreviated
![]() $\mathrm {H}^i_{\varphi ,{\mathfrak {Z}}_n}(N)^{\Gamma _L}$
by
$\mathrm {H}^i_{\varphi ,{\mathfrak {Z}}_n}(N)^{\Gamma _L}$
by
![]() $\mathrm {H}^i(N)$
. Moreover, the maps
$\mathrm {H}^i(N)$
. Moreover, the maps
![]() $\digamma _{/f}^1(\tilde {M})$
,
$\digamma _{/f}^1(\tilde {M})$
,
![]() $\digamma ^2(\tilde {M}) $
and similarly
$\digamma ^2(\tilde {M}) $
and similarly
![]() $\digamma _{f}^1(\tilde {M}): \mathrm {H}^1(\tilde {M})_f\to (H^1({M})/ H^1({M})_f)^*$
are induced from the complex isomorphism
$\digamma _{f}^1(\tilde {M}): \mathrm {H}^1(\tilde {M})_f\to (H^1({M})/ H^1({M})_f)^*$
are induced from the complex isomorphism
![]() ${K_{\varphi ,{{\mathfrak {Z}}}}(\tilde {M})}\cong K_{\varphi ,{\mathfrak {Z}}}(M )^*[-2]$
from (24). Taking duals gives the following commutative diagram with exact rows
${K_{\varphi ,{{\mathfrak {Z}}}}(\tilde {M})}\cong K_{\varphi ,{\mathfrak {Z}}}(M )^*[-2]$
from (24). Taking duals gives the following commutative diagram with exact rows

Upon noting that
![]() $\digamma ^2(\tilde {M})^*=\digamma ^0({M}) $
while
$\digamma ^2(\tilde {M})^*=\digamma ^0({M}) $
while
![]() $\digamma ^1(\tilde {M})^*=-\digamma ^1({M}) $
, whence also
$\digamma ^1(\tilde {M})^*=-\digamma ^1({M}) $
, whence also
![]() $\digamma ^1_{/f}(\tilde {M})^*=-\digamma ^1_f({M}) $
, we obtain the modified commutative diagram with exact rows
$\digamma ^1_{/f}(\tilde {M})^*=-\digamma ^1_f({M}) $
, we obtain the modified commutative diagram with exact rows

Combining this diagram with the analogue of diagram (69) for M instead of
![]() $\tilde {M}$
we obtain the commutative diagram
$\tilde {M}$
we obtain the commutative diagram

Finally, one has the commutative diagram

because of Remark 7.13 and since changing u to
![]() $-u$
requires the change
$-u$
requires the change
![]() $t_{LT}$
to
$t_{LT}$
to
![]() $-t_{LT}$
(compare with [Reference Nakamura36, Rem. 3.5] which applies analogously here) in the definition of
$-t_{LT}$
(compare with [Reference Nakamura36, Rem. 3.5] which applies analogously here) in the definition of
![]() $f_{M_0,u}$
above. Then (ii) follows from (68),(72) and (73) while the proof of (i) is literally the same as in (loc. cit.).
$f_{M_0,u}$
above. Then (ii) follows from (68),(72) and (73) while the proof of (i) is literally the same as in (loc. cit.).
Remark 7.15. As in [Reference Nakamura36, Rem. 3.5] one shows property (iii) for
![]() $ \varepsilon ^{dR}_{L,u}(M_0)$
using Remark 7.11:
$ \varepsilon ^{dR}_{L,u}(M_0)$
using Remark 7.11:
for all
![]() $a\in o_L^\times .$
$a\in o_L^\times .$
8 Epsilon-isomorphisms for (Lubin-Tate deformations of) rank one modules
In order to construct the Epsilon-isomorphism for rank one modules M in
![]() $\mathfrak {M}^{an}(K)$
we shall construct it on the level of the deformation
$\mathfrak {M}^{an}(K)$
we shall construct it on the level of the deformation
![]() $\mathbf {Dfm}(M)$
of M (introduced in §4.2) and descend the results to
$\mathbf {Dfm}(M)$
of M (introduced in §4.2) and descend the results to
![]() $M.$
As this deformation lives over the character variety
$M.$
As this deformation lives over the character variety
![]() $\mathfrak {X}_{\Gamma _L}$
(base changed to K) of the locally L-analytic group
$\mathfrak {X}_{\Gamma _L}$
(base changed to K) of the locally L-analytic group
![]() $\Gamma _L$
, we can use density arguments to deduce many of its properties just from its de Rham points.
$\Gamma _L$
, we can use density arguments to deduce many of its properties just from its de Rham points.
Definition 8.1. Using that the complexes
![]() $C_n^{\bullet }:=K_{\Psi ,D(\Gamma _L,K)}(\mathbf {Dfm}_n(M))$
are perfect by Theorem 4.6 (1) we can apply our definition
$C_n^{\bullet }:=K_{\Psi ,D(\Gamma _L,K)}(\mathbf {Dfm}_n(M))$
are perfect by Theorem 4.6 (1) we can apply our definition
which defines a (graded) line-bundle on
![]() $\mathfrak {X}_{\Gamma _L}$
by (2) of the same theorem, with global sections
$\mathfrak {X}_{\Gamma _L}$
by (2) of the same theorem, with global sections
From the proof of Theorem 4.10 we know that for the derived limit
![]() $C^{\bullet }$
and for every n,
$C^{\bullet }$
and for every n,
in
![]() $D(\mathcal {O}_{\mathfrak {X}_{\Gamma _L}}(X_n)).$
Hence, by Definition 7.4, Remark 7.5 and again Theorem 4.10 together with Remark 4.11 we obtain
$D(\mathcal {O}_{\mathfrak {X}_{\Gamma _L}}(X_n)).$
Hence, by Definition 7.4, Remark 7.5 and again Theorem 4.10 together with Remark 4.11 we obtain
Furthermore,
We survey some preliminary results that allow us to construct an isomorphism
Let
![]() $\delta \in \Sigma _{an}.$
Using
$\delta \in \Sigma _{an}.$
Using
![]() $(\mathcal {R}_K^+(\delta ))^{\Psi =0}=(\mathcal {R}_K^+)^{\Psi =0}(\delta )$
combined with Lemma 4.19 and since
$(\mathcal {R}_K^+(\delta ))^{\Psi =0}=(\mathcal {R}_K^+)^{\Psi =0}(\delta )$
combined with Lemma 4.19 and since
![]() $\varphi (\mathbf {e}_\delta )$
differs from
$\varphi (\mathbf {e}_\delta )$
differs from
![]() $\mathbf {e}_\delta $
only by a scalar in
$\mathbf {e}_\delta $
only by a scalar in
![]() $K^\times ,$
we can take
$K^\times ,$
we can take
![]() $\eta (1,Z)\mathbf {e}_\delta $
as a
$\eta (1,Z)\mathbf {e}_\delta $
as a
![]() $D(\Gamma _L,K)$
-basis of
$D(\Gamma _L,K)$
-basis of
![]() $(\mathcal {R}_K^+(\delta ))^{\Psi =0},$
which gives rise to the Mellin isomorphism
$(\mathcal {R}_K^+(\delta ))^{\Psi =0},$
which gives rise to the Mellin isomorphism
It turns out that for technical reasons (more precisely, in order to obtain the commutative diagram (99) below), we have to renormalize the Mellin isomorphism by inserting the operator
![]() $\sigma _{-1}\in \Gamma _L$
with
$\sigma _{-1}\in \Gamma _L$
with
![]() $\chi _{\mathrm {LT}}(\sigma _{-1})=-1:$
$\chi _{\mathrm {LT}}(\sigma _{-1})=-1:$
Remark 8.2.
-
(i) The complexes
 $\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta )) \cong \mathcal {T}_\Psi ( \mathcal {R}_K(\delta )/\mathcal {R}_K(\delta )^+)$
,
$\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta )) \cong \mathcal {T}_\Psi ( \mathcal {R}_K(\delta )/\mathcal {R}_K(\delta )^+)$
,
 $\mathcal {T}_\Psi (\mathcal {R}_K(\delta )) $
and
$\mathcal {T}_\Psi (\mathcal {R}_K(\delta )) $
and
 $\mathcal {T}_\Psi (\mathcal {R}_K^+(\delta )),$
are all perfect complexes of
$\mathcal {T}_\Psi (\mathcal {R}_K^+(\delta )),$
are all perfect complexes of
 $D(\Gamma _L,K)$
-modules. Indeed, by Lemma 4.20, the cohomology groups of
$D(\Gamma _L,K)$
-modules. Indeed, by Lemma 4.20, the cohomology groups of
 $\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta ))$
are finite-dimensional K-vector spaces, whence perfect as
$\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta ))$
are finite-dimensional K-vector spaces, whence perfect as
 $D(\Gamma _L,K)$
-modules by [Reference Steingart51, Lem. 3.7] (with
$D(\Gamma _L,K)$
-modules by [Reference Steingart51, Lem. 3.7] (with
 $r=0$
and using the Fourier-isomorphism). Then [48, Tag 066U] implies that
$r=0$
and using the Fourier-isomorphism). Then [48, Tag 066U] implies that
 $\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta ))$
belongs to
$\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta ))$
belongs to
 $\mathbf {D}^b_{\mathrm {perf}}(D(\Gamma _L,K))$
. Since
$\mathbf {D}^b_{\mathrm {perf}}(D(\Gamma _L,K))$
. Since
 $\mathcal {T}_\Psi (\mathcal {R}_K(\delta )) $
is in
$\mathcal {T}_\Psi (\mathcal {R}_K(\delta )) $
is in
 $\mathbf {D}^b_{\mathrm {perf}}(D(\Gamma _L,K))$
by Theorem 4.9, so is
$\mathbf {D}^b_{\mathrm {perf}}(D(\Gamma _L,K))$
by Theorem 4.9, so is
 $\mathcal {T}_\Psi (\mathcal {R}_K^+(\delta ))$
as the third complex in an obvious exact triangle with the previous ones. The same holds for
$\mathcal {T}_\Psi (\mathcal {R}_K^+(\delta ))$
as the third complex in an obvious exact triangle with the previous ones. The same holds for
 $\mathcal {T}_\Psi (D_N(\delta ))$
and
$\mathcal {T}_\Psi (D_N(\delta ))$
and
 $\mathcal {T}_\Psi (\mathcal {R}_L^+(\delta )/D_N(\delta )) $
for similar reasons.
$\mathcal {T}_\Psi (\mathcal {R}_L^+(\delta )/D_N(\delta )) $
for similar reasons. -
(ii) Since over affinoids A the analogous conclusion of [Reference Steingart51, Lem. 3.7] - i.e., that a
 $D(\Gamma _L,A)$
-module, which is finitely generated as an A-module, is perfect - is not available, we are not sure whether the construction below also carries over to families directly. It certainly does, if
$D(\Gamma _L,A)$
-module, which is finitely generated as an A-module, is perfect - is not available, we are not sure whether the construction below also carries over to families directly. It certainly does, if
 $\mathcal {R}_A(\delta )\in \mathfrak {M}^{an}(A)$
satisfies the conditions of Remark 4.23.
$\mathcal {R}_A(\delta )\in \mathfrak {M}^{an}(A)$
satisfies the conditions of Remark 4.23.
Lemma 8.3. Let
![]() $\delta \in \Sigma _{an}$
and let
$\delta \in \Sigma _{an}$
and let
![]() $M=\mathcal {R}_K(\delta )$
be the associated
$M=\mathcal {R}_K(\delta )$
be the associated
![]() $(\varphi _L,\Gamma _L)$
-module of rank one. We denote by
$(\varphi _L,\Gamma _L)$
-module of rank one. We denote by
![]() $M^+$
the submodule
$M^+$
the submodule
![]() $\mathcal {R}_K^+(\delta ).$
We have the following isomorphisms in
$\mathcal {R}_K^+(\delta ).$
We have the following isomorphisms in
![]() $\mathcal {P}_{D(\Gamma _L,K)}:$
$\mathcal {P}_{D(\Gamma _L,K)}:$
-
(i)
 $\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M)) \cong \mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M^+))$
induced by the canonical inclusion
$\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M)) \cong \mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M^+))$
induced by the canonical inclusion
 $M^+ \subset M$
and the trivialisation of
$M^+ \subset M$
and the trivialisation of
 $\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M/M^+))$
from Lemma 4.20.
$\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M/M^+))$
from Lemma 4.20. -
(ii)
 $\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M^+)) \xrightarrow {\cong } \mathbf {d}_{D(\Gamma _L,K)}([M^+ \xrightarrow {\Psi }M^+])$
induced by
$\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M^+)) \xrightarrow {\cong } \mathbf {d}_{D(\Gamma _L,K)}([M^+ \xrightarrow {\Psi }M^+])$
induced by
 $(1-\varphi _L,\operatorname {id})$
and the trivialization of
$(1-\varphi _L,\operatorname {id})$
and the trivialization of
 $d_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (D_N(\delta )))$
.
$d_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (D_N(\delta )))$
. -
(iii)
 $(D(\Gamma _L,K),1) \cong (\mathbf {d}_{D(\Gamma _L,K)}[M^+ \xrightarrow {\Psi }M^+])^{-1}$
induced by identifying
$(D(\Gamma _L,K),1) \cong (\mathbf {d}_{D(\Gamma _L,K)}[M^+ \xrightarrow {\Psi }M^+])^{-1}$
induced by identifying
 $\ker (\Psi )$
with
$\ker (\Psi )$
with
 $D(\Gamma _L,K) $
via
$D(\Gamma _L,K) $
via
 $\mathfrak {M}_\delta \circ \sigma _{-1} .$
$\mathfrak {M}_\delta \circ \sigma _{-1} .$
Chaining these together gives an isomorphism
![]() $\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M))^{-1} \cong (D(\Gamma _L,K)(\delta ),1).$
$\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (M))^{-1} \cong (D(\Gamma _L,K)(\delta ),1).$
Proof. The first statement follows since the short exact sequence
![]() $0 \to M^+ \to M \to M/M^+ \to 0$
induces a short exact sequence of complexes. For the second statement we use that by [Reference Fourquaux and Xie22, Lem. 5.1] we have a commutative diagram with exact rows
$0 \to M^+ \to M \to M/M^+ \to 0$
induces a short exact sequence of complexes. For the second statement we use that by [Reference Fourquaux and Xie22, Lem. 5.1] we have a commutative diagram with exact rows

which induces a quasi-isomorphism between the complexes, if
![]() $\delta (\pi _L)\neq \pi _L^{-i}$
for all
$\delta (\pi _L)\neq \pi _L^{-i}$
for all
![]() $i\in \mathbb {N}.$
Otherwise, kernel and cokernel of
$i\in \mathbb {N}.$
Otherwise, kernel and cokernel of
![]() $\mathcal {R}_K^+(\delta )\xrightarrow {1-\varphi } \mathcal {R}_K^+(\delta ) $
are isomorphic to
$\mathcal {R}_K^+(\delta )\xrightarrow {1-\varphi } \mathcal {R}_K^+(\delta ) $
are isomorphic to
![]() $Kt_{LT}^i$
and can be trivialized by each other when taking determinants (formally this is achieved by replacing
$Kt_{LT}^i$
and can be trivialized by each other when taking determinants (formally this is achieved by replacing
![]() $\mathcal {R}_K^+(\delta )$
by
$\mathcal {R}_K^+(\delta )$
by
![]() $\mathcal {R}_K^+(\delta )/D_N(\delta )$
and then trivializing the determinant of
$\mathcal {R}_K^+(\delta )/D_N(\delta )$
and then trivializing the determinant of
![]() $\mathcal {T}_\Psi (D_N(\delta ))$
as in [Reference Nakamura36, (Reference Schneider40),(Reference Schneider and Teitelbaum44) in §4.1]). For the third statement we first remark that the complex
$\mathcal {T}_\Psi (D_N(\delta ))$
as in [Reference Nakamura36, (Reference Schneider40),(Reference Schneider and Teitelbaum44) in §4.1]). For the third statement we first remark that the complex
![]() $M^+ \xrightarrow {\Psi } M^+$
(concentrated in degrees
$M^+ \xrightarrow {\Psi } M^+$
(concentrated in degrees
![]() $1,2$
) is cohomologically perfect by Lemma 4.19 - using
$1,2$
) is cohomologically perfect by Lemma 4.19 - using
![]() $(\mathcal {R}_K^+(\delta ))^{\Psi =0}=(\mathcal {R}_K^+)^{\Psi =0})(\delta )$
- because on the one hand
$(\mathcal {R}_K^+(\delta ))^{\Psi =0}=(\mathcal {R}_K^+)^{\Psi =0})(\delta )$
- because on the one hand
![]() $\Psi $
is surjective and on the other hand its kernel is free over
$\Psi $
is surjective and on the other hand its kernel is free over
![]() $D(\Gamma _L,K)$
by (77). Therefore the determinant of
$D(\Gamma _L,K)$
by (77). Therefore the determinant of
![]() $M^+ \xrightarrow {\Psi } M^+$
is equal to
$M^+ \xrightarrow {\Psi } M^+$
is equal to
![]() $(D(\Gamma _L,K),1)^{-1}.$
$(D(\Gamma _L,K),1)^{-1}.$
From Lemma 8.3 we obtain finally an isomorphism (cf. [Reference Nakamura36, Def. 4.1])
which in turn induces an isomorphism over K
 $$ \begin{align} \notag \varepsilon_{D(\Gamma_L,K),u}(\mathbf{Dfm}(\mathcal{R}_K(\delta)):\mathbf{1}_{D(\Gamma_L,K)} & \xrightarrow{\mathrm{can}} \mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\Psi( \mathcal{R}_K(\delta)))\mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\Psi( \mathcal{R}_K(\delta)))^{-1}\\ & \xrightarrow{\operatorname{id} \otimes \Theta(\delta)} \mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\Psi( \mathcal{R}_K(\delta)))\Delta_{2,\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(\mathcal{R}_K(\delta)))\nonumber \\ & \xrightarrow{=} \Delta_{\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(\mathcal{R}_K(\delta))). \end{align} $$
$$ \begin{align} \notag \varepsilon_{D(\Gamma_L,K),u}(\mathbf{Dfm}(\mathcal{R}_K(\delta)):\mathbf{1}_{D(\Gamma_L,K)} & \xrightarrow{\mathrm{can}} \mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\Psi( \mathcal{R}_K(\delta)))\mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\Psi( \mathcal{R}_K(\delta)))^{-1}\\ & \xrightarrow{\operatorname{id} \otimes \Theta(\delta)} \mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\Psi( \mathcal{R}_K(\delta)))\Delta_{2,\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(\mathcal{R}_K(\delta)))\nonumber \\ & \xrightarrow{=} \Delta_{\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(\mathcal{R}_K(\delta))). \end{align} $$
Note that the map (77) depends implicitly on
![]() $u.$
If we consider instead of
$u.$
If we consider instead of
![]() $\mathcal {R}_L$
the isomorphic subring
$\mathcal {R}_L$
the isomorphic subring
![]() $\mathcal {R}_L(Z_u)$
of
$\mathcal {R}_L(Z_u)$
of
![]() $\widetilde {\mathcal {R}}_L,$
as pointed out in Remark 3.11, then for
$\widetilde {\mathcal {R}}_L,$
as pointed out in Remark 3.11, then for
![]() $a=\chi _{LT}(\gamma _a) \in o_L^\times $
we have
$a=\chi _{LT}(\gamma _a) \in o_L^\times $
we have
![]() $Z_{au} = [a](Z_u)$
and thus we get a commutative diagram
$Z_{au} = [a](Z_u)$
and thus we get a commutative diagram

Indeed, we have
 $$ \begin{align*} \mathfrak{M}_{\delta,au}(\delta_{\gamma_a^{-1}}\lambda) & =\lambda\bigg(\delta_{\gamma_a^{-1}}\big(\eta(1,Z_{au})\big)\delta_{\gamma_a^{-1}}\mathbf{e}_\delta\bigg) \\ &= \lambda\bigg( \eta(a^{-1},[a](Z_{u}))\delta(a)^{-1}\mathbf{e}_\delta\bigg)\\ & = \delta(a)^{-1} \cdot \bigg(\lambda\big( \eta(1,Z_u)\mathbf{e}_\delta\big)\bigg). \end{align*} $$
$$ \begin{align*} \mathfrak{M}_{\delta,au}(\delta_{\gamma_a^{-1}}\lambda) & =\lambda\bigg(\delta_{\gamma_a^{-1}}\big(\eta(1,Z_{au})\big)\delta_{\gamma_a^{-1}}\mathbf{e}_\delta\bigg) \\ &= \lambda\bigg( \eta(a^{-1},[a](Z_{u}))\delta(a)^{-1}\mathbf{e}_\delta\bigg)\\ & = \delta(a)^{-1} \cdot \bigg(\lambda\big( \eta(1,Z_u)\mathbf{e}_\delta\big)\bigg). \end{align*} $$
Concerning the descent, we have to distinguish the following two ways.
Remark 8.4. Let
![]() $\delta : \Gamma _L \to K^\times $
be an L-analytic character. Mapping a Dirac distribution
$\delta : \Gamma _L \to K^\times $
be an L-analytic character. Mapping a Dirac distribution
![]() $\gamma $
to
$\gamma $
to
![]() $\delta (\gamma )\mathbf {e}_{\delta }$
induces a surjection of
$\delta (\gamma )\mathbf {e}_{\delta }$
induces a surjection of
![]() $D(\Gamma _L,K)$
-modules
$D(\Gamma _L,K)$
-modules
Alternatively we may equip
![]() $D(\Gamma _L,K)$
with the
$D(\Gamma _L,K)$
with the
![]() $\Gamma _L$
-action
$\Gamma _L$
-action
![]() $\gamma \eta = [\gamma ^{-1}]\eta $
, denoting the resulting
$\gamma \eta = [\gamma ^{-1}]\eta $
, denoting the resulting
![]() $\Gamma _L$
-module by
$\Gamma _L$
-module by
![]() $D(\Gamma _L,K)^\iota $
, and map
$D(\Gamma _L,K)^\iota $
, and map
![]() $\gamma $
to
$\gamma $
to
![]() $\delta (\gamma ^{-1})\mathbf {e}_\delta $
to obtain a surjection of
$\delta (\gamma ^{-1})\mathbf {e}_\delta $
to obtain a surjection of
![]() $D(\Gamma _L,K)$
-modules
$D(\Gamma _L,K)$
-modules
Proof. Since
![]() $\delta $
is analytic
$\delta $
is analytic
![]() $K(\delta )=K\mathbf {e}_{\delta }$
comes equipped with a
$K(\delta )=K\mathbf {e}_{\delta }$
comes equipped with a
![]() $D(\Gamma _L,K)$
-module structure extending the
$D(\Gamma _L,K)$
-module structure extending the
![]() $K[\Gamma _L]$
-module structure. The map
$K[\Gamma _L]$
-module structure. The map
![]() $p_\delta $
is surjective because
$p_\delta $
is surjective because
![]() $1$
is mapped to a K-basis
$1$
is mapped to a K-basis
![]() $\mathbf {e}_\delta $
and
$\mathbf {e}_\delta $
and
![]() $D(\Gamma _L,K)$
-linear by construction. The second statement follows analogously since the inverted action is also L-analytic.
$D(\Gamma _L,K)$
-linear by construction. The second statement follows analogously since the inverted action is also L-analytic.
Now, for the descent we observe that, if
![]() $f_{\delta _0}:D(\Gamma _L,K)\to K$
arises from a character
$f_{\delta _0}:D(\Gamma _L,K)\to K$
arises from a character
![]() $\delta _0:o_L^\times \subseteq L^\times \to K^\times $
interpreted as character of
$\delta _0:o_L^\times \subseteq L^\times \to K^\times $
interpreted as character of
![]() $\Gamma _L$
, we have the following:
$\Gamma _L$
, we have the following:
Lemma 8.5. The isomorphism (74) induces the canonical isomorphism
taking the normalisation from Remark 4.11 into account, compare with [Reference Nakamura36, (34), p. 370].
Proof. We show this isomorphism for each part of
![]() $\Delta $
separately:
$\Delta $
separately:
 $$ \begin{align} \notag\Delta_{1,\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(M))\otimes_{D(\Gamma_L,K),f_{\delta_0}}K&\cong d_{K[\Gamma_L/U]}(\mathcal{T}_\psi(M(\delta_0))\otimes^{\mathbb{L}}_{D(\Gamma_L,K)}D(\Gamma_L/U))\otimes_{K[\Gamma_L/U]}K\\ \notag&\cong d_{K[\Gamma_L/U]}(\mathcal{T}_\psi(M(\delta_0))\otimes^{\mathbb{L}}_{D(U)}K)\otimes_{K[\Gamma_L/U]}K\\ \notag&\cong d_{K[\Gamma_L/U]}( K_{\Psi_L,{{\mathfrak{Z}}}} (M(\delta_0)))\otimes_{K[\Gamma_L/U]}K\\ &\cong d_{K[\Gamma_L/U]}( K_{\varphi_L,{{\mathfrak{Z}}}} (M(\delta_0)))\otimes_{K[\Gamma_L/U]}K=\Delta_{1,K}(M(\delta_0)) \end{align} $$
$$ \begin{align} \notag\Delta_{1,\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(M))\otimes_{D(\Gamma_L,K),f_{\delta_0}}K&\cong d_{K[\Gamma_L/U]}(\mathcal{T}_\psi(M(\delta_0))\otimes^{\mathbb{L}}_{D(\Gamma_L,K)}D(\Gamma_L/U))\otimes_{K[\Gamma_L/U]}K\\ \notag&\cong d_{K[\Gamma_L/U]}(\mathcal{T}_\psi(M(\delta_0))\otimes^{\mathbb{L}}_{D(U)}K)\otimes_{K[\Gamma_L/U]}K\\ \notag&\cong d_{K[\Gamma_L/U]}( K_{\Psi_L,{{\mathfrak{Z}}}} (M(\delta_0)))\otimes_{K[\Gamma_L/U]}K\\ &\cong d_{K[\Gamma_L/U]}( K_{\varphi_L,{{\mathfrak{Z}}}} (M(\delta_0)))\otimes_{K[\Gamma_L/U]}K=\Delta_{1,K}(M(\delta_0)) \end{align} $$
and
 $$ \begin{align} \Delta_{2,\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(M))\otimes_{D(\Gamma_L,K),f_{\delta_0}}K&\cong \Delta_{2,K}(M)\otimes_K D(\Gamma_L,K)\otimes_{D(\Gamma_L,K),f_{\delta_0}}K\\ \notag &\cong \Delta_{2,K}(M(\delta_0))=(K\mathbf{e}_{\delta\delta_0},1) \end{align} $$
$$ \begin{align} \Delta_{2,\mathfrak{X}_{\Gamma_L}}(\mathbf{Dfm}(M))\otimes_{D(\Gamma_L,K),f_{\delta_0}}K&\cong \Delta_{2,K}(M)\otimes_K D(\Gamma_L,K)\otimes_{D(\Gamma_L,K),f_{\delta_0}}K\\ \notag &\cong \Delta_{2,K}(M(\delta_0))=(K\mathbf{e}_{\delta\delta_0},1) \end{align} $$
using Remark 7.2.
With these preparations we are now able to state the main result of this article.
Theorem 8.6 (Local
 $\varepsilon $
-conjecture for Lubin-Tate deformations of rank one modules)
$\varepsilon $
-conjecture for Lubin-Tate deformations of rank one modules)
Let
![]() $F'/L$
be a finite subextension of K and M be a rank one analytic
$F'/L$
be a finite subextension of K and M be a rank one analytic
![]() $(\varphi _L,\Gamma _L)$
-module over
$(\varphi _L,\Gamma _L)$
-module over
![]() $\mathcal {R}_{F'}$
and denote by
$\mathcal {R}_{F'}$
and denote by
![]() $M_K$
the completed base change
$M_K$
the completed base change
![]() $M\hat {\otimes }_{F'} K$
. Then the isomorphism
$M\hat {\otimes }_{F'} K$
. Then the isomorphism
induces for every L-analytic character
![]() $\vartheta :\Gamma _L\to F^\times $
with finite intermediate extension
$\vartheta :\Gamma _L\to F^\times $
with finite intermediate extension
![]() $F'\subseteq F\subseteq K$
such that
$F'\subseteq F\subseteq K$
such that
![]() $M_K(\vartheta )$
is de Rham the following commutative diagram
$M_K(\vartheta )$
is de Rham the following commutative diagram

where the notation
![]() $f_\vartheta $
has been defined in Remark 8.4 and the specialisation isomorphism
$f_\vartheta $
has been defined in Remark 8.4 and the specialisation isomorphism
![]() $\mathrm {sp}_\vartheta $
is explained in Lemma 8.5 above. Moreover,
$\mathrm {sp}_\vartheta $
is explained in Lemma 8.5 above. Moreover,
![]() $\varepsilon _{D(\Gamma _L,K),u}(\mathbf {Dfm}(M_K)) $
is uniquely determined by this property.
$\varepsilon _{D(\Gamma _L,K),u}(\mathbf {Dfm}(M_K)) $
is uniquely determined by this property.
The uniqueness follows from the considerations in Appendix A while the specialisation property will be proved in subsection 8.4 below.
Note that the isomorphism
![]() $\varepsilon _{D(\Gamma _L,K)}(\mathbf {Dfm}(\mathcal {R}_K(\delta )) $
does not literally fit into Conjecture 7.6, because
$\varepsilon _{D(\Gamma _L,K)}(\mathbf {Dfm}(\mathcal {R}_K(\delta )) $
does not literally fit into Conjecture 7.6, because
![]() $D(\Gamma _L,K)$
is not an affinoid algebra over K. But for any morphism of rigid analytic spaces
$D(\Gamma _L,K)$
is not an affinoid algebra over K. But for any morphism of rigid analytic spaces
![]() $f:Sp(A)\to \mathfrak {X}_\Gamma $
with an affinoid algebra A (e.g.
$f:Sp(A)\to \mathfrak {X}_\Gamma $
with an affinoid algebra A (e.g.
![]() $D_n$
) over K it induces the isomorphism
$D_n$
) over K it induces the isomorphism
 $$ \begin{align*} \varepsilon_{A}(f^*\mathbf{Dfm}(\mathcal{R}_K(\delta))(Sp(A)))&:=\varepsilon_{D(\Gamma_L,K)}(\mathbf{Dfm}(\mathcal{R}_K(\delta))\otimes_{D(\Gamma_L,K)}A) \colon \\ \mathbf{1}_{A}&\xrightarrow{\cong} \Delta_{A}(f^*\mathbf{Dfm}(\mathcal{R}_K(\delta))(Sp(A))) \end{align*} $$
$$ \begin{align*} \varepsilon_{A}(f^*\mathbf{Dfm}(\mathcal{R}_K(\delta))(Sp(A)))&:=\varepsilon_{D(\Gamma_L,K)}(\mathbf{Dfm}(\mathcal{R}_K(\delta))\otimes_{D(\Gamma_L,K)}A) \colon \\ \mathbf{1}_{A}&\xrightarrow{\cong} \Delta_{A}(f^*\mathbf{Dfm}(\mathcal{R}_K(\delta))(Sp(A))) \end{align*} $$
which provides instances of the conjectured type. Note that for the inclusion
![]() $f:Sp(D_n)\hookrightarrow \mathfrak {X}_\Gamma $
we obtain
$f:Sp(D_n)\hookrightarrow \mathfrak {X}_\Gamma $
we obtain
8.1 Property (v)
Specialization to the case considered by Nakamura requires some special care, because we used a different definition of
![]() $\varepsilon $
-constants. As discussed in 7.7 the assumption that K contains
$\varepsilon $
-constants. As discussed in 7.7 the assumption that K contains
![]() $L^{ab}$
can be dropped since
$L^{ab}$
can be dropped since
![]() $L_\infty $
contains the p-power roots of unity. We can thus even assume
$L_\infty $
contains the p-power roots of unity. We can thus even assume
![]() $K=\mathbb {Q}_p$
in the construction of the de Rham
$K=\mathbb {Q}_p$
in the construction of the de Rham
![]() $\varepsilon $
-constants. Similarly we can take
$\varepsilon $
-constants. Similarly we can take
![]() $\Omega =1$
and hence do not need any special assumptions on K in order to make use of p-adic Fourier theory.
$\Omega =1$
and hence do not need any special assumptions on K in order to make use of p-adic Fourier theory.
Proposition 8.7. Assume
![]() $L= \mathbb {Q}_p,$
assume
$L= \mathbb {Q}_p,$
assume
![]() $\pi _L=p.$
take
$\pi _L=p.$
take
![]() $u_n = \zeta _{p^n}-1$
for a compatible system of p-power roots of unity and choose a
$u_n = \zeta _{p^n}-1$
for a compatible system of p-power roots of unity and choose a
![]() $\gamma \in \Gamma _{\mathbb {Q}_p},$
which is a topological generator of the torsion-free part, such that
$\gamma \in \Gamma _{\mathbb {Q}_p},$
which is a topological generator of the torsion-free part, such that
![]() $\log _0(\chi _{cyc}(\gamma )) = 1,$
and take
$\log _0(\chi _{cyc}(\gamma )) = 1,$
and take
![]() $\Omega _{\mathbb {Q}_p} = 1.$
Then, if one assumes
$\Omega _{\mathbb {Q}_p} = 1.$
Then, if one assumes
![]() $K=\mathbb {Q}_p$
, our construction agrees with the one in [Reference Nakamura36].
$K=\mathbb {Q}_p$
, our construction agrees with the one in [Reference Nakamura36].
Proof. Note that by a density argument and by property (vi) it suffices to see that the constructions in the de Rham case coincide. The condition of L-analyticity is automatic, if
![]() $L=\mathbb {Q}_p.$
We remark that the complex
$L=\mathbb {Q}_p.$
We remark that the complex
![]() $K^\bullet _{\varphi ,\mathfrak {Z}}(-)$
considered by us specialises to a variant of the usual Herr-complex as we can take
$K^\bullet _{\varphi ,\mathfrak {Z}}(-)$
considered by us specialises to a variant of the usual Herr-complex as we can take
![]() $\mathfrak {Z}=\gamma -1$
, but there is a small difference to [Reference Nakamura36, Definition 2.10]. The order of
$\mathfrak {Z}=\gamma -1$
, but there is a small difference to [Reference Nakamura36, Definition 2.10]. The order of
![]() $\varphi -1$
and
$\varphi -1$
and
![]() $\gamma -1$
is exchanged (which poses no problem), Nakamura uses a topological generator
$\gamma -1$
is exchanged (which poses no problem), Nakamura uses a topological generator
![]() $\gamma _{Na}$
of
$\gamma _{Na}$
of
![]() $\Gamma /\Delta ,$
with
$\Gamma /\Delta ,$
with
![]() $\Delta = \Gamma _{p-\text {power-torsion}}$
while we use a generator of the free part. In the case
$\Delta = \Gamma _{p-\text {power-torsion}}$
while we use a generator of the free part. In the case
![]() $p=2$
the terms of Nakamura’s complex are
$p=2$
the terms of Nakamura’s complex are
![]() $M^{\Delta }.$
In this case our choice of
$M^{\Delta }.$
In this case our choice of
![]() $\gamma $
is a valid choice for the variant in (loc.cit.) while in the case
$\gamma $
is a valid choice for the variant in (loc.cit.) while in the case
![]() $p\neq 2$
we can arrange that
$p\neq 2$
we can arrange that
![]() $\gamma _{Na}^{p-1} = \gamma .$
In both cases the torsion subgroup
$\gamma _{Na}^{p-1} = \gamma .$
In both cases the torsion subgroup
![]() $\Delta ' \subseteq \Gamma $
is a split subgroup and taking
$\Delta ' \subseteq \Gamma $
is a split subgroup and taking
![]() $\Delta '$
-invariants is exact in characteristic
$\Delta '$
-invariants is exact in characteristic
![]() $0.$
Let
$0.$
Let
![]() $U = \overline {\langle \gamma \rangle } \subseteq \Gamma .$
For
$U = \overline {\langle \gamma \rangle } \subseteq \Gamma .$
For
![]() $p=2$
we have
$p=2$
we have
![]() $\Delta = \Delta '$
and plugging in the isomorphism
$\Delta = \Delta '$
and plugging in the isomorphism
![]() $M^\Delta \cong M/\Delta $
and
$M^\Delta \cong M/\Delta $
and
![]() $\Delta \cong \Gamma /U$
we see that our
$\Delta \cong \Gamma /U$
we see that our
![]() $\mathbb {Q}_p\otimes _{\mathbb {Q}_p[\Delta ]}K_{\varphi ,\mathfrak {Z}}(M)$
is canonically isomorphic to the complex considered in (loc.cit.). For
$\mathbb {Q}_p\otimes _{\mathbb {Q}_p[\Delta ]}K_{\varphi ,\mathfrak {Z}}(M)$
is canonically isomorphic to the complex considered in (loc.cit.). For
![]() $p\neq 2$
we can consider instead the natural map of complexes
$p\neq 2$
we can consider instead the natural map of complexes
given by
![]() $m \mapsto \frac {1}{p-1} \sum _{g \in \Delta '}gm$
in both degrees, which induces a quasi-isomorphism onto the
$m \mapsto \frac {1}{p-1} \sum _{g \in \Delta '}gm$
in both degrees, which induces a quasi-isomorphism onto the
![]() $\Delta '$
-(co)invariants of the right-hand side and induces a corresponding quasi-isomorphism of the Herr-complexes by taking
$\Delta '$
-(co)invariants of the right-hand side and induces a corresponding quasi-isomorphism of the Herr-complexes by taking
![]() $\varphi -1$
-cones. We can thus conclude that the fundamental lines are canonically isomorphic to the ones considered by Nakamura. Similarly the exponential maps are the same. Because
$\varphi -1$
-cones. We can thus conclude that the fundamental lines are canonically isomorphic to the ones considered by Nakamura. Similarly the exponential maps are the same. Because
![]() $\pi _L=p=q$
we see that the character
$\pi _L=p=q$
we see that the character
![]() $\chi $
is just
$\chi $
is just
![]() $\chi _{cyc}$
and the duality pairing
$\chi _{cyc}$
and the duality pairing
![]() $\langle -,- \rangle _{\tilde {M}}$
from section 4.3 is the pairing used by Nakamura. In (66) we use
$\langle -,- \rangle _{\tilde {M}}$
from section 4.3 is the pairing used by Nakamura. In (66) we use
![]() $\langle -,-\rangle _M$
which by the same reasoning corresponds to the pairing used by Nakamura, namely the duality pairing for
$\langle -,-\rangle _M$
which by the same reasoning corresponds to the pairing used by Nakamura, namely the duality pairing for
![]() $M_0 = \tilde {M}$
. The assumptions on
$M_0 = \tilde {M}$
. The assumptions on
![]() $\gamma $
and
$\gamma $
and
![]() $\Omega $
avoid the problem discussed in 7.7 (ii) concerning normalisation factors and the appearance of
$\Omega $
avoid the problem discussed in 7.7 (ii) concerning normalisation factors and the appearance of
![]() $\Omega $
in the
$\Omega $
in the
![]() $\Gamma $
-factor. Finally, the series
$\Gamma $
-factor. Finally, the series
![]() $\eta (1,Z)$
is just
$\eta (1,Z)$
is just
![]() $1 + Z$
and we can view
$1 + Z$
and we can view
![]() $\eta (1,(u_n \otimes 1))$
appearing in the construction of the equivariant
$\eta (1,(u_n \otimes 1))$
appearing in the construction of the equivariant
![]() $\varepsilon $
-constants as an element of
$\varepsilon $
-constants as an element of
![]() $L_\infty ,$
in fact we have
$L_\infty ,$
in fact we have
![]() $\eta (1,u_n\otimes 1) = \zeta _{p^n}$
under the isomorphism
$\eta (1,u_n\otimes 1) = \zeta _{p^n}$
under the isomorphism
![]() $L_\infty \otimes _{\mathbb {Q}_p} \mathbb {Q}_p \cong L_\infty .$
Combining all of the above shows that our
$L_\infty \otimes _{\mathbb {Q}_p} \mathbb {Q}_p \cong L_\infty .$
Combining all of the above shows that our
![]() $\varepsilon $
-constants constructed in the de Rham case agree with those in Nakamura’s work.
$\varepsilon $
-constants constructed in the de Rham case agree with those in Nakamura’s work.
8.2 Property (i)
For all
![]() $f:A\to A'$
, such that we are able to construct the
$f:A\to A'$
, such that we are able to construct the
![]() $\varepsilon $
-isomorphism as above for A and
$\varepsilon $
-isomorphism as above for A and
![]() $A'$
, the base change property (i) with respect to
$A'$
, the base change property (i) with respect to
![]() $f:A\to A'$
obviously holds by construction.
$f:A\to A'$
obviously holds by construction.
8.3 Property (iii)
We can rephrase the diagram (79) to the following commutative diagram for any
![]() $a\in o_L^\times $
$a\in o_L^\times $

where
![]() $[a]$
acts on
$[a]$
acts on
![]() $D(\Gamma _L,K)(\delta )$
as
$D(\Gamma _L,K)(\delta )$
as
![]() $\delta _{\gamma _a}^{-1}\cdot \delta (a)$
(here
$\delta _{\gamma _a}^{-1}\cdot \delta (a)$
(here
![]() $\delta _{\gamma _a}$
denotes the dirac distribution attached to
$\delta _{\gamma _a}$
denotes the dirac distribution attached to
![]() $\gamma _a\in \Gamma _L$
with
$\gamma _a\in \Gamma _L$
with
![]() $\chi _{LT}(\gamma _a)=a$
). Note that the action on
$\chi _{LT}(\gamma _a)=a$
). Note that the action on
![]() $N:=\mathbf {Dfm}(\mathcal {R}_K(\delta ))$
with respect to the basis
$N:=\mathbf {Dfm}(\mathcal {R}_K(\delta ))$
with respect to the basis
![]() $1 \otimes e_\delta $
is given precisely by the character
$1 \otimes e_\delta $
is given precisely by the character
![]() $\overline {\delta }\colon \Gamma _L \to D(\Gamma _L,K)^\times; \gamma \mapsto (\delta _{\gamma })^{-1}\delta (\chi _{LT}(\gamma ))$
and hence property (iii) follows from the above diagram by specialising along
$\overline {\delta }\colon \Gamma _L \to D(\Gamma _L,K)^\times; \gamma \mapsto (\delta _{\gamma })^{-1}\delta (\chi _{LT}(\gamma ))$
and hence property (iii) follows from the above diagram by specialising along
![]() $D(\Gamma _L,K)(\delta ) \to K(\delta ).$
$D(\Gamma _L,K)(\delta ) \to K(\delta ).$
8.4 Descent
For
![]() $\delta \in \Sigma _{an}(F)$
with F a finite extension of L, we consider the decomposition
$\delta \in \Sigma _{an}(F)$
with F a finite extension of L, we consider the decomposition
![]() $\delta =\delta ^{\mathrm {un}}\delta _0$
as in section 3.4 and define on the basis of (78)
$\delta =\delta ^{\mathrm {un}}\delta _0$
as in section 3.4 and define on the basis of (78)
as
![]() $\varepsilon _{D(\Gamma _L,K)}(\mathbf {Dfm}(\mathcal {R}_K(\delta ^{\mathrm {un}}))\otimes _{D(\Gamma _L,K),f_{\delta _0}}K) $
followed by the isomorphism from Lemma 8.5. In order to make this definition more explicit we have to understand the isomorphism
$\varepsilon _{D(\Gamma _L,K)}(\mathbf {Dfm}(\mathcal {R}_K(\delta ^{\mathrm {un}}))\otimes _{D(\Gamma _L,K),f_{\delta _0}}K) $
followed by the isomorphism from Lemma 8.5. In order to make this definition more explicit we have to understand the isomorphism
![]() $\bar {\Theta }(\delta ):=\Theta (\delta ^{\mathrm {un}})\otimes _{D(\Gamma _L,K),f_{\delta _0}}L$
, which we will consider as an isomorphism
$\bar {\Theta }(\delta ):=\Theta (\delta ^{\mathrm {un}})\otimes _{D(\Gamma _L,K),f_{\delta _0}}L$
, which we will consider as an isomorphism
 $$\begin{align*}\bar{\Theta}(\delta):\bigotimes_{i=0}^2 \mathbf{d}_{K[\Gamma_L/U]}(H^i_{\Psi_L,{{\mathfrak{Z}}}}(\mathcal{R}_K(\delta)))^{(-1)^{i+1}}\otimes_{K[\Gamma_L/U]}K\cong (K\mathbf{e}_\delta,1) \end{align*}$$
$$\begin{align*}\bar{\Theta}(\delta):\bigotimes_{i=0}^2 \mathbf{d}_{K[\Gamma_L/U]}(H^i_{\Psi_L,{{\mathfrak{Z}}}}(\mathcal{R}_K(\delta)))^{(-1)^{i+1}}\otimes_{K[\Gamma_L/U]}K\cong (K\mathbf{e}_\delta,1) \end{align*}$$
by using (81) and the inverse of the natural isomorphism
 $$ \begin{align*} \mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\psi( \mathcal{R}_L(\delta)))\otimes_{D(\Gamma_L,K),f_{\delta_0}}K&\cong \mathbf{d}_{K[\Gamma_L/U]}( K_{\Psi_L,{{\mathfrak{Z}}}} (M(\delta_0)))\otimes_{K[\Gamma_L/U]}K\\ &\cong \bigotimes_{i=0}^2 \mathbf{d}_{K[\Gamma_L/U]}(H^i_{\Psi_L,{{\mathfrak{Z}}}}(\mathcal{R}_K(\delta)))^{(-1)^{i}}\otimes_{K[\Gamma_L/U]}K \end{align*} $$
$$ \begin{align*} \mathbf{d}_{D(\Gamma_L,K)}(\mathcal{T}_\psi( \mathcal{R}_L(\delta)))\otimes_{D(\Gamma_L,K),f_{\delta_0}}K&\cong \mathbf{d}_{K[\Gamma_L/U]}( K_{\Psi_L,{{\mathfrak{Z}}}} (M(\delta_0)))\otimes_{K[\Gamma_L/U]}K\\ &\cong \bigotimes_{i=0}^2 \mathbf{d}_{K[\Gamma_L/U]}(H^i_{\Psi_L,{{\mathfrak{Z}}}}(\mathcal{R}_K(\delta)))^{(-1)^{i}}\otimes_{K[\Gamma_L/U]}K \end{align*} $$
induced from (80) using properties of the determinant functor from section 7.1.
From the exact sequences (29), (31), (32) we derive the following exact sequences and isomorphisms:
 $$ \begin{align} 0\to &H^0_{\Psi,{{\mathfrak{Z}}}}(\mathcal{R}_K^+(\delta))\to H^0_{\Psi,{{\mathfrak{Z}}}}(\mathcal{R}_K (\delta))\to H^0_{\Psi,{{\mathfrak{Z}}}}(LA(o_L)(\chi^{-1}\delta))\to \\ \notag & H^1_{{{\mathfrak{Z}}}}(H^0_\Psi(\mathcal{R}_K^+(\delta)))\to H^1_{{{\mathfrak{Z}}}}(H^0_\Psi(\mathcal{R}_K(\delta)))\to H^1_{{{\mathfrak{Z}}}}(H^0_\Psi(LA(o_L)(\chi^{-1}\delta)))\to 0, \end{align} $$
$$ \begin{align} 0\to &H^0_{\Psi,{{\mathfrak{Z}}}}(\mathcal{R}_K^+(\delta))\to H^0_{\Psi,{{\mathfrak{Z}}}}(\mathcal{R}_K (\delta))\to H^0_{\Psi,{{\mathfrak{Z}}}}(LA(o_L)(\chi^{-1}\delta))\to \\ \notag & H^1_{{{\mathfrak{Z}}}}(H^0_\Psi(\mathcal{R}_K^+(\delta)))\to H^1_{{{\mathfrak{Z}}}}(H^0_\Psi(\mathcal{R}_K(\delta)))\to H^1_{{{\mathfrak{Z}}}}(H^0_\Psi(LA(o_L)(\chi^{-1}\delta)))\to 0, \end{align} $$
For the descent it is useful to recall that the determinant functor
![]() $\mathbf {d}_?$
commutes with taking the derived tensor product
$\mathbf {d}_?$
commutes with taking the derived tensor product
![]() $-\otimes ^{\mathbb {L}}_{D(\Gamma _L,K),f_{\delta _0}}K$
. E.g. the additivity on short exact sequences above turns into the additivity on the associated long exact sequences of cohomology groups below. Finally, the determinant functor commutes with attached spectral sequences by [Reference Venjakob55].
$-\otimes ^{\mathbb {L}}_{D(\Gamma _L,K),f_{\delta _0}}K$
. E.g. the additivity on short exact sequences above turns into the additivity on the associated long exact sequences of cohomology groups below. Finally, the determinant functor commutes with attached spectral sequences by [Reference Venjakob55].
8.5 Verification of the conditions (iv), (vi)
In this subsection, we prove the condition (iv) using density arguments in the process of verifying the condition (vi). Indeed, it suffices to prove (vi) as the duality statement for de Rham characters was shown in 7.14 and by Zariski density of the de Rham characters (see Corollary A.4) the validity of property (iv) holds in general once we establish (vi), i.e., the interpolation property in the de Rham case. We follow the strategy of Nakamura and consider first a generic L-analytic de Rham character of weight
![]() $k.$
The case
$k.$
The case
![]() $k\leq 0$
boils down to Proposition 8.11. The case
$k\leq 0$
boils down to Proposition 8.11. The case
![]() $k\geq 1$
is treated in Proposition 8.14. The remaining so-called exceptional case is treated in Section 8.5.3.
$k\geq 1$
is treated in Proposition 8.14. The remaining so-called exceptional case is treated in Section 8.5.3.
8.5.1 Twisting
We define the operator
![]() $\partial \colon \mathcal {R}_K\to \mathcal {R}_K, f\mapsto \frac {1}{\log ^{\prime }_{LT}}\frac {df}{dZ}=\frac {df}{ dt_{LT}},$
and the residuum map
$\partial \colon \mathcal {R}_K\to \mathcal {R}_K, f\mapsto \frac {1}{\log ^{\prime }_{LT}}\frac {df}{dZ}=\frac {df}{ dt_{LT}},$
and the residuum map
![]() $Res\colon \mathcal {R}_K\to K, f\mapsto res(fdt_{LT})$
with
$Res\colon \mathcal {R}_K\to K, f\mapsto res(fdt_{LT})$
with
![]() $res(\sum _{i\in \mathbb {Z}} a_iZ^idZ)=a_{-1}.$
Extending theses maps coefficientwise, i.e., applying it to f in
$res(\sum _{i\in \mathbb {Z}} a_iZ^idZ)=a_{-1}.$
Extending theses maps coefficientwise, i.e., applying it to f in
![]() $f\mathbf {e}_\delta $
and using [Reference Fourquaux and Xie22, Lem. 2.11, 2.12] we obtain an exact sequenceFootnote
23
$f\mathbf {e}_\delta $
and using [Reference Fourquaux and Xie22, Lem. 2.11, 2.12] we obtain an exact sequenceFootnote
23
It is well-known that the partial operator
![]() $\partial \colon \mathcal {R}_K\to \mathcal {R}_K$
is related to twisting, see e.g. [Reference Schneider and Venjakob46, §4.3.9]:Footnote
24
$\partial \colon \mathcal {R}_K\to \mathcal {R}_K$
is related to twisting, see e.g. [Reference Schneider and Venjakob46, §4.3.9]:Footnote
24

Here, for a locally L-analytic character
![]() $\rho : \Gamma _L \rightarrow K^\times $
we denote by
$\rho : \Gamma _L \rightarrow K^\times $
we denote by
the isomorphism which on Dirac distributions satisfies
![]() $Tw_\rho (\delta _g) = \rho (g) \delta _g$
.
$Tw_\rho (\delta _g) = \rho (g) \delta _g$
.
Using for
![]() $\mathbf {d}_{D(\Gamma _L,K)}\mathcal {T}_\Psi (K(\delta '))$
,
$\mathbf {d}_{D(\Gamma _L,K)}\mathcal {T}_\Psi (K(\delta '))$
,
![]() $\delta '=\delta ,\delta |x|^{-1},$
the trivialization by identity, the operator
$\delta '=\delta ,\delta |x|^{-1},$
the trivialization by identity, the operator
![]() $\partial $
induces via the above exact sequence the isomorphism
$\partial $
induces via the above exact sequence the isomorphism
which also descends to an isomorphism
Moreover, we have isomorphisms
and
by sending
![]() $f\mathbf {e}_{\delta }$
to
$f\mathbf {e}_{\delta }$
to
![]() $\frac {-1}{\Omega }f\mathbf {e}_{x\delta }$
. Altogether we obtain an isomorphism
$\frac {-1}{\Omega }f\mathbf {e}_{x\delta }$
. Altogether we obtain an isomorphism
which also descends to an isomorphism
Using diagram (90) and the definition of
![]() $\epsilon _{D(\Gamma _L,K)}(\mathbf {Dfm}(\mathcal {R}_K(\delta ))$
and
$\epsilon _{D(\Gamma _L,K)}(\mathbf {Dfm}(\mathcal {R}_K(\delta ))$
and
![]() $ \epsilon _{L}(\mathcal {R}_K(\delta ))$
respectively, we conclude the following
$ \epsilon _{L}(\mathcal {R}_K(\delta ))$
respectively, we conclude the following
Proposition 8.8. If
![]() $\delta \neq \mathbf {1}, |x|$
, then there are canonical equalities
$\delta \neq \mathbf {1}, |x|$
, then there are canonical equalities
Proof. Since the second statement follows by descent from the first one, we only have to consider the case of the deformation following the construction in Lemma 8.3 step by step. Regarding 8.3(i) we observe that the operator
![]() $\partial $
restricts to an operator
$\partial $
restricts to an operator
![]() $\mathcal {R}_K^+(\delta )\to \mathcal {R}_K^+(x\delta ) $
while it induces the operator
$\mathcal {R}_K^+(\delta )\to \mathcal {R}_K^+(x\delta ) $
while it induces the operator
![]() $LA(o_L)(\chi ^{-1}\delta ) \to LA(o_L)(\chi ^{-1}x\delta ), \phi \mathbf {e}_{\chi ^{-1}\delta }\mapsto \Omega x \phi \mathbf {e}_{\chi ^{-1}x\delta },$
which can easily be derived from Remark 3.12 (v) combined with the exactness of (89). The compatibility with
$LA(o_L)(\chi ^{-1}\delta ) \to LA(o_L)(\chi ^{-1}x\delta ), \phi \mathbf {e}_{\chi ^{-1}\delta }\mapsto \Omega x \phi \mathbf {e}_{\chi ^{-1}x\delta },$
which can easily be derived from Remark 3.12 (v) combined with the exactness of (89). The compatibility with
![]() $1-\varphi _L$
in 8.3(ii) is a consequence of Remark 3.12 (i). Finally, the compatibility of
$1-\varphi _L$
in 8.3(ii) is a consequence of Remark 3.12 (i). Finally, the compatibility of
![]() $\partial $
with
$\partial $
with
![]() $\mathfrak {M}_\delta \circ \sigma _{-1} $
in 8.3(iii) follows from diagram (90) together with the
$\mathfrak {M}_\delta \circ \sigma _{-1} $
in 8.3(iii) follows from diagram (90) together with the
![]() $\sigma _{-1}$
in the definition of (77) using 3.12 (ii). Combining both yields the factor
$\sigma _{-1}$
in the definition of (77) using 3.12 (ii). Combining both yields the factor
![]() $-\Omega $
which cancels against the factor in the definition of
$-\Omega $
which cancels against the factor in the definition of
![]() $\partial _{|\Delta _2}.$
One can check that the twisting construction is compatible with the various trivializations involved.
$\partial _{|\Delta _2}.$
One can check that the twisting construction is compatible with the various trivializations involved.
Proposition 8.9. Let
![]() $\delta \in \Sigma ^{an}(F)$
with
$\delta \in \Sigma ^{an}(F)$
with
![]() $F/L$
finite such that
$F/L$
finite such that
![]() $\mathcal {R}_F(\delta )$
is a de Rham
$\mathcal {R}_F(\delta )$
is a de Rham
![]() $(\varphi ,\Gamma _L)$
-module with Hodge-Tate weight different form zero. Then we have the equality
$(\varphi ,\Gamma _L)$
-module with Hodge-Tate weight different form zero. Then we have the equality
Proof. The proof is analogous to that of [Reference Nakamura36, 4.14] upon noting that
![]() $\Gamma ^*(k)$
has to be replaced by
$\Gamma ^*(k)$
has to be replaced by
![]() $\Omega ^k\Gamma ^*(k)$
.
$\Omega ^k\Gamma ^*(k)$
.
Since
![]() $\varepsilon ^{dR}$
and
$\varepsilon ^{dR}$
and
![]() $\varepsilon $
are compatible with respect to
$\varepsilon $
are compatible with respect to
![]() $\partial $
by the above propositions, it can be used to transport the validity of the Conjecture between characters
$\partial $
by the above propositions, it can be used to transport the validity of the Conjecture between characters
![]() $\delta x $
and
$\delta x $
and
![]() $\delta .$
$\delta .$
8.5.2 Generic case
This subsection has been inspired by [Reference Nakamura36, 4B1] and [Reference Venjakob54]. In this subsection
![]() $U=\Gamma _n$
and
$U=\Gamma _n$
and
![]() ${{\mathfrak {Z}}}={{\mathfrak {Z}}_n}$
for an appropriate sufficiently large
${{\mathfrak {Z}}}={{\mathfrak {Z}}_n}$
for an appropriate sufficiently large
![]() $n\gg 0,$
which might be adapted to the specific situation. This is possible because due to our normalisations the constructions and the factorization of the descent over
$n\gg 0,$
which might be adapted to the specific situation. This is possible because due to our normalisations the constructions and the factorization of the descent over
![]() $K[\Gamma _L/\Gamma _n]$
are independent of n, see Lemma 8.5, (80), Definition 5.11 and Remark 4.11.
$K[\Gamma _L/\Gamma _n]$
are independent of n, see Lemma 8.5, (80), Definition 5.11 and Remark 4.11.
Lemma 8.10. For
![]() $\delta \in \Sigma _{gen}{(F)}$
we have
$\delta \in \Sigma _{gen}{(F)}$
we have
 $$ \begin{align} H^i_{\Psi,{{\mathfrak{Z}}}}(LA(o_L)(\chi^{-1}\delta))&=H^i_{\Psi,{{\mathfrak{Z}}}}(Pol_{\leq N}(o_L)){ = H^i_{\Psi,{{\mathfrak{Z}}}}(D_N(\delta))=0,} \\\notag H^1_{{{\mathfrak{Z}}}}(H^0_{\Psi}(LA(o_L)(\chi^{-1}\delta))) &=H^0_{{{\mathfrak{Z}}}}(H^1_{\Psi}(LA(o_L)(\chi^{-1}\delta)))=0 \end{align} $$
$$ \begin{align} H^i_{\Psi,{{\mathfrak{Z}}}}(LA(o_L)(\chi^{-1}\delta))&=H^i_{\Psi,{{\mathfrak{Z}}}}(Pol_{\leq N}(o_L)){ = H^i_{\Psi,{{\mathfrak{Z}}}}(D_N(\delta))=0,} \\\notag H^1_{{{\mathfrak{Z}}}}(H^0_{\Psi}(LA(o_L)(\chi^{-1}\delta))) &=H^0_{{{\mathfrak{Z}}}}(H^1_{\Psi}(LA(o_L)(\chi^{-1}\delta)))=0 \end{align} $$
for all i and
![]() $N\geq 0,$
and
$N\geq 0,$
and
for
![]() $i\neq 1,$
and
$i\neq 1,$
and
Proof. The first claim follows from (34),(36) and Lemma 4.20. The second follows from Lemma 4.5 (combined with Remark 4.21) and 4.22 (there for
![]() $\Gamma _L$
instead of U, but applying the result to all twists by characters of the finite group
$\Gamma _L$
instead of U, but applying the result to all twists by characters of the finite group
![]() $\Gamma _L/U$
also implies the statement concerning U) combined with (83) and (84). The last assertion follows from the previous ones combined with (88),(86),(85).
$\Gamma _L/U$
also implies the statement concerning U) combined with (83) and (84). The last assertion follows from the previous ones combined with (88),(86),(85).
By construction according to Lemma 8.3 and using Lemma 8.10 we see that
![]() $\bar {\Theta }(\delta )$
arises - upon taking determinants and descending further by
$\bar {\Theta }(\delta )$
arises - upon taking determinants and descending further by
![]() $-\otimes ^{\mathbb {L}}_{K[\Gamma _L/U]}K$
- by the composite of
$-\otimes ^{\mathbb {L}}_{K[\Gamma _L/U]}K$
- by the composite of
-
(i) (the inverse of) the isomorphism
 $H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\delta )))\cong H^1_{\Psi ,{{\mathfrak {Z}}}}(\mathcal {R}_K(\delta ))$
together with the trivializations of
$H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\delta )))\cong H^1_{\Psi ,{{\mathfrak {Z}}}}(\mathcal {R}_K(\delta ))$
together with the trivializations of
 $\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta )))$
and
$\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi ( LA(o_L)(\chi ^{-1}\delta )))$
and
 $ \mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi ( Pol_{\leq N}(o_L) (\chi ^{-1}\delta )))$
,
$ \mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi ( Pol_{\leq N}(o_L) (\chi ^{-1}\delta )))$
, -
(ii)
 $H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\delta )))\cong H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\delta )^{\Psi =0})$
induced by
$H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\delta )))\cong H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\delta )^{\Psi =0})$
induced by
 $1-\varphi ,$
together with the trivialisation of kernel and cokernel of
$1-\varphi ,$
together with the trivialisation of kernel and cokernel of
 $\mathcal {R}_K^+(\delta )\xrightarrow {1-\varphi } \mathcal {R}_K^+(\delta ) $
- each isomorphic to
$\mathcal {R}_K^+(\delta )\xrightarrow {1-\varphi } \mathcal {R}_K^+(\delta ) $
- each isomorphic to
 $Kt_{LT}^i$
- respectively with the trivialization of
$Kt_{LT}^i$
- respectively with the trivialization of
 $\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (D_N(\delta )))$
and
$\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (D_N(\delta )))$
and -
(iii)
 $H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\delta )^{\Psi =0})\xrightarrow {C_{Tr}({{\mathfrak {Z}}_n})}(\mathcal {R}_K^+(\delta )^{\Psi =0})_U \cong D(\Gamma _L,K)_U\cong K[\Gamma _L/U]$
up to choosing basis elements and using the Mellin transform
$H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\delta )^{\Psi =0})\xrightarrow {C_{Tr}({{\mathfrak {Z}}_n})}(\mathcal {R}_K^+(\delta )^{\Psi =0})_U \cong D(\Gamma _L,K)_U\cong K[\Gamma _L/U]$
up to choosing basis elements and using the Mellin transform
 $\mathfrak {M}_\delta \circ \sigma _{-1}.$
$\mathfrak {M}_\delta \circ \sigma _{-1}.$
Altogether - up to the isomorphism
![]() $H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\delta ))) \cong H^1_{\Psi ,{{\mathfrak {Z}}}}(\mathcal {R}_K(\delta )), [x]\mapsto [(0, x)]$
- this amounts to
$H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\delta ))) \cong H^1_{\Psi ,{{\mathfrak {Z}}}}(\mathcal {R}_K(\delta )), [x]\mapsto [(0, x)]$
- this amounts to
For the remainder of the section we assume in addition that
![]() $\delta $
is de Rham. We have to compare (94) with
$\delta $
is de Rham. We have to compare (94) with
By the commutativity of the upper square in the (second) diagram of Lemma 8.12 one immediately sees that a class
![]() $[A_\mu \mathbf {e}_\delta ]$
is mapped under (94) to
$[A_\mu \mathbf {e}_\delta ]$
is mapped under (94) to
![]() $pr_{\Gamma _n}(Tw_{\delta ^{-1}}(\mathrm {Res}_{o_L^\times }(\mu )))\mathbf {e}_\delta $
while under (95) to
$pr_{\Gamma _n}(Tw_{\delta ^{-1}}(\mathrm {Res}_{o_L^\times }(\mu )))\mathbf {e}_\delta $
while under (95) to
![]() $\iota _n(A_\mu \mathbf {e}_\delta )_{|t_{LT}=0}=\theta \circ \iota _n(A_\mu \mathbf {e}_\delta )$
by Definition 5.11 combined with Lemma 5.10. Recall that
$\iota _n(A_\mu \mathbf {e}_\delta )_{|t_{LT}=0}=\theta \circ \iota _n(A_\mu \mathbf {e}_\delta )$
by Definition 5.11 combined with Lemma 5.10. Recall that
![]() $\theta $
was defined above Definition 3.13. Consider the
$\theta $
was defined above Definition 3.13. Consider the
![]() $K[\Gamma _L/\Gamma _n] $
-linear map
$K[\Gamma _L/\Gamma _n] $
-linear map
whose
![]() $\rho $
-component, for
$\rho $
-component, for
![]() $\rho $
running through the characters of
$\rho $
running through the characters of
![]() $G_n:=\Gamma _L/\Gamma _n$
, is given as the K-linear map
$G_n:=\Gamma _L/\Gamma _n$
, is given as the K-linear map
upon noting that
![]() $\mathbf {D}_{\mathrm {dR}} (\mathcal {R}_K(\delta '))=(L_\infty \otimes _LK\frac {1}{t_{LT}^k}\mathbf {e}_{\delta '})^{\Gamma _L}.$
Here
$\mathbf {D}_{\mathrm {dR}} (\mathcal {R}_K(\delta '))=(L_\infty \otimes _LK\frac {1}{t_{LT}^k}\mathbf {e}_{\delta '})^{\Gamma _L}.$
Here
![]() $\mathfrak {e}_\rho :=\frac {1}{|G_n|}\sum _{g\in G_n} \rho (g^{-1})g\in K[G_n]$
denotes the idempotent attached to
$\mathfrak {e}_\rho :=\frac {1}{|G_n|}\sum _{g\in G_n} \rho (g^{-1})g\in K[G_n]$
denotes the idempotent attached to
![]() $\rho $
satisfying
$\rho $
satisfying
![]() $g\mathfrak {e}_\rho =\rho (g)\mathfrak {e}_\rho $
for all
$g\mathfrak {e}_\rho =\rho (g)\mathfrak {e}_\rho $
for all
![]() $g\in G_n$
, while for an analytic character
$g\in G_n$
, while for an analytic character
![]() $\delta ':L^\times \to (F')^\times $
(of weight
$\delta ':L^\times \to (F')^\times $
(of weight
![]() $k\leq 0$
) we set
$k\leq 0$
) we set
 $$ \begin{align} \mathfrak{C}(\delta'):=\frac{(-\Omega)^k}{(-k)!}\left\{ \begin{array}{ll} { \tilde{\varepsilon}(\mathcal{R}_{K}(\delta'),u)^{-1},} & \text{if } a(\delta')\neq 0; \\ \frac{\det(1-q^{-1}\varphi^{-1}|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}{\det(1-\varphi|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}, & \text{otherwise} \end{array} \right. \end{align} $$
$$ \begin{align} \mathfrak{C}(\delta'):=\frac{(-\Omega)^k}{(-k)!}\left\{ \begin{array}{ll} { \tilde{\varepsilon}(\mathcal{R}_{K}(\delta'),u)^{-1},} & \text{if } a(\delta')\neq 0; \\ \frac{\det(1-q^{-1}\varphi^{-1}|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}{\det(1-\varphi|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}, & \text{otherwise} \end{array} \right. \end{align} $$
in
![]() $L_n\otimes _LK.$
Unravelling the definition of
$L_n\otimes _LK.$
Unravelling the definition of
![]() $\varepsilon ^{dR}_{L,u}$
and using Proposition 5.16 one easily sees that part (vi) of Conjecture 7.6 is equivalent, for
$\varepsilon ^{dR}_{L,u}$
and using Proposition 5.16 one easily sees that part (vi) of Conjecture 7.6 is equivalent, for
![]() $k\leq 0,$
to the next
$k\leq 0,$
to the next
Proposition 8.11 (Explicit reciprocity formula)
Let
![]() $\delta =\delta _{lc}x^k$
be de Rham. For
$\delta =\delta _{lc}x^k$
be de Rham. For
![]() $k\leq 0,$
the following diagram is commutative:Footnote
25
$k\leq 0,$
the following diagram is commutative:Footnote
25

i.e., a class
![]() $[A_\mu \mathbf {e}_\delta ]\in H^1_{{\mathfrak {Z}}_n}(H^0_\Psi (\mathcal {R}_K^+(\delta )))^{\Gamma _L} \cong H^1_{\Psi ,{\mathfrak {Z}}_n}(\mathcal {R}_K(\delta ))^{\Gamma _L},$
is mapped under
$[A_\mu \mathbf {e}_\delta ]\in H^1_{{\mathfrak {Z}}_n}(H^0_\Psi (\mathcal {R}_K^+(\delta )))^{\Gamma _L} \cong H^1_{\Psi ,{\mathfrak {Z}}_n}(\mathcal {R}_K(\delta ))^{\Gamma _L},$
is mapped under
![]() $\exp ^{*}$
to
$\exp ^{*}$
to
 $$\begin{align*}\mathfrak{C}(\delta )p_{\delta^{-1}}( \mu))\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }=\mathfrak{C}(\delta )\int_{ o_L^\times}\delta(x)^{-1} \mu(x)\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }.\end{align*}$$
$$\begin{align*}\mathfrak{C}(\delta )p_{\delta^{-1}}( \mu))\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }=\mathfrak{C}(\delta )\int_{ o_L^\times}\delta(x)^{-1} \mu(x)\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }.\end{align*}$$
The left hand triangle in (99) is induced by the commutative diagrams

and

The middle triangle is commutative by Lemma 5.10 upon recalling that
by (20), while the commutativity of the right upper triangle of diagram (99) follows for
![]() $k=0$
from the (lower rectangle of the) following lemma (applied to each
$k=0$
from the (lower rectangle of the) following lemma (applied to each
![]() $\rho $
-component) which explains how
$\rho $
-component) which explains how
![]() $\epsilon $
-constants show up naturally in the descent procedure (cf. with [Reference Benois and Berger2, Lem. 4.9/Cor. 4.10] and [Reference Nakamura36, Prop. 4.11] in the cyclotomic situation):
$\epsilon $
-constants show up naturally in the descent procedure (cf. with [Reference Benois and Berger2, Lem. 4.9/Cor. 4.10] and [Reference Nakamura36, Prop. 4.11] in the cyclotomic situation):
Lemma 8.12. Let
![]() $\delta $
be a locally constant character. Then the following diagram is commutative:Footnote
26
$\delta $
be a locally constant character. Then the following diagram is commutative:Footnote
26

Proof. The commutativity of the upper rectangle in this diagram is an immediate consequence of Lemma 4.19, that of the triangle is immediate from the definitions, while that for the lower part is obviously equivalent to the commutativity of the outer diagram

where
![]() $p_{\delta }(\mu ):=\int _{ o_L^\times }\delta (x) \mu (x)$
denotes the evaluation at a character
$p_{\delta }(\mu ):=\int _{ o_L^\times }\delta (x) \mu (x)$
denotes the evaluation at a character
![]() $\delta. $
In order to check this, assume
$\delta. $
In order to check this, assume
![]() $p\neq 2$
(the case
$p\neq 2$
(the case
![]() $p=2$
can be dealt with similarly as in the proof of [Reference Nakamura36, Pro. 4.11]) and first assume that
$p=2$
can be dealt with similarly as in the proof of [Reference Nakamura36, Pro. 4.11]) and first assume that
![]() $n:=a(\delta )\geq 1.$
Then we have
$n:=a(\delta )\geq 1.$
Then we have
 $$ \begin{align*} \mathrm{Tr}_{K_n/K}\circ \theta\circ \iota_n(A_\mu \mathbf{e}_\delta)&= \sum_{i\in (o_L/\pi_L^n)^\times}\sigma_i\left( \theta\circ \iota_n(A_\mu \mathbf{e}_\delta)\right)\\ &=\sum_{i\in (o_L/\pi_L^n)^\times}\sigma_i\left( \iota_n(A_\mu \mathbf{e}_\delta)_{|t_{LT}=0}\right)\\ &=\sum_{i\in (o_L/\pi_L^n)^\times}\sigma_i\left( A_\mu( u_n\otimes1) \varphi^{-n}(\mathbf{e}_\delta) \right)\;\;\;\; \text{ in } L_n\otimes K\mathbf{e}_\delta\\ &=\bigg(\sum_{i\in (o_L/\pi_L^n)^\times}\delta(i) A_\mu( \sigma_i\tau(u_n)\otimes1) \bigg)_\tau \varphi^{-n}(\mathbf{e}_\delta) \;\;\;\; \text{ in } \prod_\tau K\mathbf{e}_\delta\\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{i\in (o_L/\pi_L^n)^\times}\delta(i) \int_{o_L}\eta(x,\sigma_i\tau(u_n))\mu(x) \bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i)\left( \int_{o_L}\eta(xi,\tau(u_n))\mu(x) \bigg)_\tau \mathbf{e}_\delta \right)\\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i)\sum_{j\in o_L/\pi_L^n} \eta(ji,\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{j\in o_L/\pi_L^n}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i) \eta(ji,\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &\stackrel{ (\ast)}{=}\bigg( \frac{1}{\delta(\pi_L)^n}\sum_{j\in (o_L/\pi_L^n)^\times}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i) \eta(ji,\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{j\in (o_L/\pi_L^n)^\times} \sum_{i'\in (o_L/\pi_L^n)^\times} \delta(i'j^{-1}) \eta(i',\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\left(\sum_{i\in (o_L/\pi_L^n)^\times}\delta(i)\eta(i,\tau(u_n))\right)\sum_{j\in (o_L/\pi_L^n)^\times} \delta(j^{-1}) \int_{j+\pi_L^n o_L}\mu(x)\bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(q^{-n(\psi_u)} \epsilon_K(L,K(\delta^{-1}),\psi_{\hat{\tau}u},dx) \int_{ o_L^\times}\delta(x)^{-1} \mu(x) \bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(q^{-n(\psi_u)} \epsilon_K(L,K(\delta^{-1}),\psi_{\hat{\tau}u},dx) p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(q^{a(\delta) }\epsilon_K(L,\delta^{-1}|-|,\psi(x)_{\hat{\tau}u},dx)p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(\frac{\delta(-1)q^{a(\delta)+n(\psi_{\hat{\tau}u})}}{ \epsilon_K(L,\delta,\psi_{\hat{\tau}u},dx)}p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \bigg)_\tau\mathbf{e}_\delta. \end{align*} $$
$$ \begin{align*} \mathrm{Tr}_{K_n/K}\circ \theta\circ \iota_n(A_\mu \mathbf{e}_\delta)&= \sum_{i\in (o_L/\pi_L^n)^\times}\sigma_i\left( \theta\circ \iota_n(A_\mu \mathbf{e}_\delta)\right)\\ &=\sum_{i\in (o_L/\pi_L^n)^\times}\sigma_i\left( \iota_n(A_\mu \mathbf{e}_\delta)_{|t_{LT}=0}\right)\\ &=\sum_{i\in (o_L/\pi_L^n)^\times}\sigma_i\left( A_\mu( u_n\otimes1) \varphi^{-n}(\mathbf{e}_\delta) \right)\;\;\;\; \text{ in } L_n\otimes K\mathbf{e}_\delta\\ &=\bigg(\sum_{i\in (o_L/\pi_L^n)^\times}\delta(i) A_\mu( \sigma_i\tau(u_n)\otimes1) \bigg)_\tau \varphi^{-n}(\mathbf{e}_\delta) \;\;\;\; \text{ in } \prod_\tau K\mathbf{e}_\delta\\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{i\in (o_L/\pi_L^n)^\times}\delta(i) \int_{o_L}\eta(x,\sigma_i\tau(u_n))\mu(x) \bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i)\left( \int_{o_L}\eta(xi,\tau(u_n))\mu(x) \bigg)_\tau \mathbf{e}_\delta \right)\\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i)\sum_{j\in o_L/\pi_L^n} \eta(ji,\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{j\in o_L/\pi_L^n}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i) \eta(ji,\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &\stackrel{ (\ast)}{=}\bigg( \frac{1}{\delta(\pi_L)^n}\sum_{j\in (o_L/\pi_L^n)^\times}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i) \eta(ji,\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\sum_{j\in (o_L/\pi_L^n)^\times} \sum_{i'\in (o_L/\pi_L^n)^\times} \delta(i'j^{-1}) \eta(i',\tau(u_n)) \int_{j+\pi_L^n o_L}\mu(x) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(\frac{1}{\delta(\pi_L)^n}\left(\sum_{i\in (o_L/\pi_L^n)^\times}\delta(i)\eta(i,\tau(u_n))\right)\sum_{j\in (o_L/\pi_L^n)^\times} \delta(j^{-1}) \int_{j+\pi_L^n o_L}\mu(x)\bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(q^{-n(\psi_u)} \epsilon_K(L,K(\delta^{-1}),\psi_{\hat{\tau}u},dx) \int_{ o_L^\times}\delta(x)^{-1} \mu(x) \bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(q^{-n(\psi_u)} \epsilon_K(L,K(\delta^{-1}),\psi_{\hat{\tau}u},dx) p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \bigg)_\tau\mathbf{e}_\delta \\ &=\bigg(q^{a(\delta) }\epsilon_K(L,\delta^{-1}|-|,\psi(x)_{\hat{\tau}u},dx)p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \bigg)_\tau \mathbf{e}_\delta \\ &=\bigg(\frac{\delta(-1)q^{a(\delta)+n(\psi_{\hat{\tau}u})}}{ \epsilon_K(L,\delta,\psi_{\hat{\tau}u},dx)}p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \bigg)_\tau\mathbf{e}_\delta. \end{align*} $$
In the two last equalities we used (61) and (62). Moreover, the equation
![]() $(\ast )$
requires part (i) of the next lemma. Finally, by Remark 6.2 we have
$(\ast )$
requires part (i) of the next lemma. Finally, by Remark 6.2 we have
![]() $n(\psi _u)=0,$
whence the result in this case as
$n(\psi _u)=0,$
whence the result in this case as
![]() $[K_n:K]=q^{n-1}(q-1)$
upon comparing with (98), Example 7.9 and Definition 7.10.
$[K_n:K]=q^{n-1}(q-1)$
upon comparing with (98), Example 7.9 and Definition 7.10.
Now we consider the case
![]() $a(\delta )=0$
and obtain
$a(\delta )=0$
and obtain
 $$ \begin{align*} \mathrm{Tr}_{K_1/K}\circ \theta\circ \iota_1(A_\mu \mathbf{e}_\delta)&= \sum_{i\in (o_L/\pi_L)^\times}\sigma_i\left( \theta\circ \iota_1(A_\mu \mathbf{e}_\delta)\right)\\ &=\sum_{i\in (o_L/\pi_L)^\times}\sigma_i\left( \iota_1(A_\mu \mathbf{e}_\delta)_{|t_{LT}=0}\right)\\ &=\sum_{i\in (o_L/\pi_L)^\times}\sigma_i\left( A_\mu(u_1\otimes 1) \varphi^{-1}(\mathbf{e}_\delta) \right)\\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{i\in (o_L/\pi_L)^\times} \int_{o_L}\eta(x,\sigma_i\tau(u_1))\mu(x) \right)_\tau \mathbf{e}_\delta \\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{i\in (o_L/\pi_L)^\times} \int_{o_L}\eta(xi,\tau(u_1))\mu(x)\right)_\tau \mathbf{e}_\delta \\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{i\in (o_L/\pi_L)^\times} \sum_{j\in o_L/\pi_L} \eta(ji,\tau(u_1)) \int_{j+\pi_L o_L}\mu(x)\right)_\tau \mathbf{e}_\delta \\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{j\in o_L/\pi_L}\sum_{i\in (o_L/\pi_L)^\times} \eta(ji,\tau(u_1)) \int_{j+\pi_L o_L}\mu(x) \right)_\tau\mathbf{e}_\delta \\ &\stackrel{ (\ast)}{=}\left(\frac{1}{\delta(\pi_L)}\left( (q-1)\int_{\pi_L o_L}\mu(x)-\int_{ o_L^\times}\mu(x)\right) \right)_\tau\mathbf{e}_\delta \\ &=\frac{1}{\delta(\pi_L)}\left( (q-1)\frac{\delta(\pi_L)}{1-\delta(\pi_L)}-1\right) \int_{ o_L^\times}\mu(x) \mathbf{e}_\delta \\ &=q \frac{1-\frac{1}{q\delta(\pi_L)}}{1-\delta(\pi_L)} p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \mathbf{e}_\delta, \end{align*} $$
$$ \begin{align*} \mathrm{Tr}_{K_1/K}\circ \theta\circ \iota_1(A_\mu \mathbf{e}_\delta)&= \sum_{i\in (o_L/\pi_L)^\times}\sigma_i\left( \theta\circ \iota_1(A_\mu \mathbf{e}_\delta)\right)\\ &=\sum_{i\in (o_L/\pi_L)^\times}\sigma_i\left( \iota_1(A_\mu \mathbf{e}_\delta)_{|t_{LT}=0}\right)\\ &=\sum_{i\in (o_L/\pi_L)^\times}\sigma_i\left( A_\mu(u_1\otimes 1) \varphi^{-1}(\mathbf{e}_\delta) \right)\\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{i\in (o_L/\pi_L)^\times} \int_{o_L}\eta(x,\sigma_i\tau(u_1))\mu(x) \right)_\tau \mathbf{e}_\delta \\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{i\in (o_L/\pi_L)^\times} \int_{o_L}\eta(xi,\tau(u_1))\mu(x)\right)_\tau \mathbf{e}_\delta \\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{i\in (o_L/\pi_L)^\times} \sum_{j\in o_L/\pi_L} \eta(ji,\tau(u_1)) \int_{j+\pi_L o_L}\mu(x)\right)_\tau \mathbf{e}_\delta \\ &=\left(\frac{1}{\delta(\pi_L)}\sum_{j\in o_L/\pi_L}\sum_{i\in (o_L/\pi_L)^\times} \eta(ji,\tau(u_1)) \int_{j+\pi_L o_L}\mu(x) \right)_\tau\mathbf{e}_\delta \\ &\stackrel{ (\ast)}{=}\left(\frac{1}{\delta(\pi_L)}\left( (q-1)\int_{\pi_L o_L}\mu(x)-\int_{ o_L^\times}\mu(x)\right) \right)_\tau\mathbf{e}_\delta \\ &=\frac{1}{\delta(\pi_L)}\left( (q-1)\frac{\delta(\pi_L)}{1-\delta(\pi_L)}-1\right) \int_{ o_L^\times}\mu(x) \mathbf{e}_\delta \\ &=q \frac{1-\frac{1}{q\delta(\pi_L)}}{1-\delta(\pi_L)} p_{\delta^{-1}}({\mathrm{Res}_{o_L^\times}\mu} ) \mathbf{e}_\delta, \end{align*} $$
where the fact that
![]() $\delta (i)=1$
for all
$\delta (i)=1$
for all
![]() $i\in o_L^\times $
by assumption is used in the fourth and last equality, while part (ii) from the next Lemma is the justification for the equality
$i\in o_L^\times $
by assumption is used in the fourth and last equality, while part (ii) from the next Lemma is the justification for the equality
![]() $(\ast )$
. The second last equality can be derived from the observation that the condition
$(\ast )$
. The second last equality can be derived from the observation that the condition
![]() $A_\mu \mathbf {e}_\delta \in \mathcal {R}_K^+(\delta )^{\Psi =1}$
implies that
$A_\mu \mathbf {e}_\delta \in \mathcal {R}_K^+(\delta )^{\Psi =1}$
implies that
![]() $\Psi (A_\mu )=\delta (\pi _L)A_\mu $
by the product formula, whence
$\Psi (A_\mu )=\delta (\pi _L)A_\mu $
by the product formula, whence
 $$ \begin{align*} \int_{\pi_L o_L}\mu(x) & =\int_{ o_L}\Psi(\mu)(x)= \delta(\pi_L)\int_{ o_L}\mu(x) =\delta(\pi_L) \left( \int_{ o_L^\times}\mu(x)+\int_{\pi_L o_L}\mu(x) \right). \end{align*} $$
$$ \begin{align*} \int_{\pi_L o_L}\mu(x) & =\int_{ o_L}\Psi(\mu)(x)= \delta(\pi_L)\int_{ o_L}\mu(x) =\delta(\pi_L) \left( \int_{ o_L^\times}\mu(x)+\int_{\pi_L o_L}\mu(x) \right). \end{align*} $$
It follows that
![]() $\int _{\pi _L o_L}\mu (x) =\frac {\delta ( \pi _L)}{1-\delta (\pi _L)}\int _{ o_L^\times }\mu (x).$
$\int _{\pi _L o_L}\mu (x) =\frac {\delta ( \pi _L)}{1-\delta (\pi _L)}\int _{ o_L^\times }\mu (x).$
Lemma 8.13. Assuming
![]() $n=a(\delta )\geq 1$
we have for all
$n=a(\delta )\geq 1$
we have for all
![]() $j\in o_L/\pi _L^n$
$j\in o_L/\pi _L^n$
-
(i)
 $\sum _{i\in (o_L/\pi _L^n)^\times } \delta (i)\eta (ij,u_n)=0$
if
$\sum _{i\in (o_L/\pi _L^n)^\times } \delta (i)\eta (ij,u_n)=0$
if
 $\pi _L|j,$
$\pi _L|j,$
-
(ii)
 $ \sum _{i\in (o_L/\pi _L)^\times } \eta (ji,u_1)=\left \{ \begin {array}{@{}ll} q-1, & \text {if}\ \pi _L|j; \\ -1, & \text {otherwise.} \end {array} \right .$
$ \sum _{i\in (o_L/\pi _L)^\times } \eta (ji,u_1)=\left \{ \begin {array}{@{}ll} q-1, & \text {if}\ \pi _L|j; \\ -1, & \text {otherwise.} \end {array} \right .$
Proof. If
![]() $\pi _L$
divides
$\pi _L$
divides
![]() $j,$
then
$j,$
then
![]() $\eta (ji,u_1)=1$
for all i and both statements (for
$\eta (ji,u_1)=1$
for all i and both statements (for
![]() $n=1$
) follow by a character sum argument (Note that the assumption
$n=1$
) follow by a character sum argument (Note that the assumption
![]() $n \geq 1$
asserts that
$n \geq 1$
asserts that
![]() $\delta $
is not trivial). Otherwise the claim (ii) follows from the character formula
$\delta $
is not trivial). Otherwise the claim (ii) follows from the character formula
![]() $\sum _{o_L/\pi _L}\eta (i,u_1)=0$
while for (i) we may assume
$\sum _{o_L/\pi _L}\eta (i,u_1)=0$
while for (i) we may assume
![]() $n \geq 2.$
We first show
$n \geq 2.$
We first show
 $$ \begin{align} \sum_{i \in (o_L/\pi_L^n)^{\times}, i \equiv r\ \mod j'} \delta(i) =0\end{align} $$
$$ \begin{align} \sum_{i \in (o_L/\pi_L^n)^{\times}, i \equiv r\ \mod j'} \delta(i) =0\end{align} $$
for every
![]() $r\in (o_L/\pi _L^n)^\times $
and every proper divisor
$r\in (o_L/\pi _L^n)^\times $
and every proper divisor
![]() $j' \mid \pi _L^n.$
By shifting it suffices to consider
$j' \mid \pi _L^n.$
By shifting it suffices to consider
![]() $r =1.$
In this case we are looking at
$r =1.$
In this case we are looking at
where
![]() $H = \operatorname {ker}(o_L/\pi _L^n)^\times \to (o_L/(j'))^\times .$
This character sum can only be different from zero if
$H = \operatorname {ker}(o_L/\pi _L^n)^\times \to (o_L/(j'))^\times .$
This character sum can only be different from zero if
![]() $\delta $
is trivial on the subgroup
$\delta $
is trivial on the subgroup
![]() $H,$
contradicting the minimality of
$H,$
contradicting the minimality of
![]() $n.$
Without loss of generality assume that
$n.$
Without loss of generality assume that
![]() $v_{\pi _L}(j)\leq n$
, whence
$v_{\pi _L}(j)\leq n$
, whence
![]() $\pi _L^{n}/j$
belongs to
$\pi _L^{n}/j$
belongs to
![]() $o_L.$
Now let
$o_L.$
Now let
![]() $\mathfrak {R}$
be a system of representatives of
$\mathfrak {R}$
be a system of representatives of
![]() $(o_L/(\pi _L^{n}/j))^{\times }$
inside
$(o_L/(\pi _L^{n}/j))^{\times }$
inside
![]() $(o_L/\pi _L^n)^\times $
and rewrite
$(o_L/\pi _L^n)^\times $
and rewrite
 $$ \begin{align*}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i)\eta(ij,u_n)= \sum_{r \in \mathfrak{R}}\left( \eta(jr,u_n) \left(\sum_{i, i \equiv r\ \mod \pi_L^n/j}\delta(i)\right) \right) =0\end{align*} $$
$$ \begin{align*}\sum_{i\in (o_L/\pi_L^n)^\times} \delta(i)\eta(ij,u_n)= \sum_{r \in \mathfrak{R}}\left( \eta(jr,u_n) \left(\sum_{i, i \equiv r\ \mod \pi_L^n/j}\delta(i)\right) \right) =0\end{align*} $$
by (102) applied to
![]() $j' = \pi _L^n /j,$
using that
$j' = \pi _L^n /j,$
using that
![]() $\eta (ji,u_n) = \eta (jr,u_n)$
if
$\eta (ji,u_n) = \eta (jr,u_n)$
if
![]() $i \equiv r\ \mod \pi _L^n/j.$
$i \equiv r\ \mod \pi _L^n/j.$
Proposition 8.11 for
![]() $k<0$
we will be reduced to the case
$k<0$
we will be reduced to the case
![]() $k=0$
by a twisting argument based on the previous subsection 8.5.1. Similarly the cases
$k=0$
by a twisting argument based on the previous subsection 8.5.1. Similarly the cases
![]() $k>1$
of the following proposition will also be reduced to the case
$k>1$
of the following proposition will also be reduced to the case
![]() $k=1$
. But first we have to slightly modify our notation. Consider the
$k=1$
. But first we have to slightly modify our notation. Consider the
![]() $K[\Gamma _L/\Gamma _n] $
-linear map
$K[\Gamma _L/\Gamma _n] $
-linear map
whose
![]() $\rho $
-component, for
$\rho $
-component, for
![]() $\rho $
running through the characters of
$\rho $
running through the characters of
![]() $G_n:=\Gamma _L/\Gamma _n$
, is given as the K-linear map
$G_n:=\Gamma _L/\Gamma _n$
, is given as the K-linear map
with
 $$ \begin{align} \mathfrak{C}'(\delta'):=\Omega^k(k-1)!\left\{ \begin{array}{ll} { \tilde{\varepsilon}(\mathcal{R}_{K}(\delta'),u)^{-1},} & \text{if } a(\delta')\neq 0; \\ \frac{\det(1-q^{-1}\varphi^{-1}|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}{\det(1-\varphi|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}, & \text{otherwise,} \end{array} \right. \end{align} $$
$$ \begin{align} \mathfrak{C}'(\delta'):=\Omega^k(k-1)!\left\{ \begin{array}{ll} { \tilde{\varepsilon}(\mathcal{R}_{K}(\delta'),u)^{-1},} & \text{if } a(\delta')\neq 0; \\ \frac{\det(1-q^{-1}\varphi^{-1}|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}{\det(1-\varphi|\mathbf{D}_{\text{cris}}(\mathcal{R}_K(\delta')))}, & \text{otherwise,} \end{array} \right. \end{align} $$
in
![]() $L_n\otimes _LK.$
$L_n\otimes _LK.$
Proposition 8.14 (Explicit reciprocity formula)
Let
![]() $\delta =\delta _{lc}x^k$
be de Rham. For
$\delta =\delta _{lc}x^k$
be de Rham. For
![]() $k\geq 1,$
the following diagram is commutative:
$k\geq 1,$
the following diagram is commutative:

i.e., a class
![]() $[A_\mu \mathbf {e}_\delta ]\in H^1_{{\mathfrak {Z}}_n}(H^0_\Psi (\mathcal {R}_K^+(\delta )))^{\Gamma _L} \cong H^1_{\Psi ,{\mathfrak {Z}}_n}(\mathcal {R}_K(\delta ))^{\Gamma _L},$
is mapped under
$[A_\mu \mathbf {e}_\delta ]\in H^1_{{\mathfrak {Z}}_n}(H^0_\Psi (\mathcal {R}_K^+(\delta )))^{\Gamma _L} \cong H^1_{\Psi ,{\mathfrak {Z}}_n}(\mathcal {R}_K(\delta ))^{\Gamma _L},$
is mapped under
![]() $\exp ^{-1}_{\mathcal {R}_K(\delta )}$
to
$\exp ^{-1}_{\mathcal {R}_K(\delta )}$
to
 $$\begin{align*}\mathfrak{C}'(\delta )p_{\delta^{-1}}( \mu))\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }=\mathfrak{C}'(\delta )\int_{ o_L^\times}\delta(x)^{-1} \mu(x)\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }.\end{align*}$$
$$\begin{align*}\mathfrak{C}'(\delta )p_{\delta^{-1}}( \mu))\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }=\mathfrak{C}'(\delta )\int_{ o_L^\times}\delta(x)^{-1} \mu(x)\frac{1}{t_{LT}^k}\mathbf{e}_{\delta }.\end{align*}$$
Proof. As mentioned earlier - by the twisting technique - we only have to show the case
![]() $k=1$
(i.e.
$k=1$
(i.e.
![]() $\delta =\tilde {\delta }x$
). We will show the commutativity of the following diagram
$\delta =\tilde {\delta }x$
). We will show the commutativity of the following diagram

on the image of
![]() $(\mathcal {R}_K^+(\tilde {\delta }))^{\Psi =1}$
in
$(\mathcal {R}_K^+(\tilde {\delta }))^{\Psi =1}$
in
![]() $H^1_{\Psi ,{{\mathfrak {Z}}_n}}(\mathcal {R}_K(\tilde {\delta })) $
, which together with the diagram (90) implies the desired formula by comparing the cases
$H^1_{\Psi ,{{\mathfrak {Z}}_n}}(\mathcal {R}_K(\tilde {\delta })) $
, which together with the diagram (90) implies the desired formula by comparing the cases
![]() $k=1$
and
$k=1$
and
![]() $k=0.$
To this end assume
$k=0.$
To this end assume
with
![]() $f\mathbf {e}_{\tilde {\delta }}\in (\mathcal {R}^+_K(\tilde {\delta }))^{\Psi =1}$
. Then it follows from definition 5.11 in combination with Lemma 5.10 that
$f\mathbf {e}_{\tilde {\delta }}\in (\mathcal {R}^+_K(\tilde {\delta }))^{\Psi =1}$
. Then it follows from definition 5.11 in combination with Lemma 5.10 that
for sufficiently large
![]() $n\geq 1,$
i.e., there exists
$n\geq 1,$
i.e., there exists
![]() $y_n\in \mathbf {D}_{\operatorname {\mathrm {dif}}}^+(\mathcal {R}_K(\tilde {\delta }) )$
such that
$y_n\in \mathbf {D}_{\operatorname {\mathrm {dif}}}^+(\mathcal {R}_K(\tilde {\delta }) )$
such that
By Remark 4.3 the element
![]() $\nabla \in \operatorname {Lie}(\Gamma _n)$
is divisible by
$\nabla \in \operatorname {Lie}(\Gamma _n)$
is divisible by
![]() $\mathfrak {Z}_n$
in
$\mathfrak {Z}_n$
in
![]() $D(\Gamma _n,K)$
and the quotient
$D(\Gamma _n,K)$
and the quotient
![]() $\frac {\nabla }{\mathfrak {Z}_n}$
corresponds to
$\frac {\nabla }{\mathfrak {Z}_n}$
corresponds to
![]() $\frac {\Omega }{\pi _L^n}\frac {\log _{LT}(Z)}{Z}$
under the Fourier-LT-isomorphism, which takes the value
$\frac {\Omega }{\pi _L^n}\frac {\log _{LT}(Z)}{Z}$
under the Fourier-LT-isomorphism, which takes the value
![]() $\frac {\Omega }{\pi _L^n}=C_g(\mathfrak {Z}_n)$
at
$\frac {\Omega }{\pi _L^n}=C_g(\mathfrak {Z}_n)$
at
![]() $Z=0$
(cf. (51)).
$Z=0$
(cf. (51)).
We wish to apply the
![]() $\Psi $
-version of Proposition 5.9 (1) for
$\Psi $
-version of Proposition 5.9 (1) for
![]() $\exp _{\mathcal {R}_K({\delta })}^{(n)} $
with
$\exp _{\mathcal {R}_K({\delta })}^{(n)} $
with
![]() $\tilde {x}=\frac {\nabla }{{\mathfrak {Z}}_n}\big (\frac {f}{t_{LT}}\mathbf {e}_\delta \big )$
and
$\tilde {x}=\frac {\nabla }{{\mathfrak {Z}}_n}\big (\frac {f}{t_{LT}}\mathbf {e}_\delta \big )$
and
![]() $x=\frac {\alpha }{t_{LT}}\mathbf {e}_{\delta }$
, which would tell us that
$x=\frac {\alpha }{t_{LT}}\mathbf {e}_{\delta }$
, which would tell us that
 $$ \begin{align*} \exp_{\mathcal{R}_K({\delta})}^{(n)}(\frac{\alpha}{t_{LT}}\mathbf{e}_{\delta}) & =[(\Psi-1)\frac{\nabla}{{\mathfrak{Z}}_n}\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big), {{\mathfrak{Z}}_n} \frac{\nabla}{{\mathfrak{Z}}_n}\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big)]\\ & =[ \frac{\nabla}{{\mathfrak{Z}}_n}(\Psi-1)\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big), {\nabla}\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big) ] \\ & =[0,\partial(f) \mathbf{e}_\delta ], \end{align*} $$
$$ \begin{align*} \exp_{\mathcal{R}_K({\delta})}^{(n)}(\frac{\alpha}{t_{LT}}\mathbf{e}_{\delta}) & =[(\Psi-1)\frac{\nabla}{{\mathfrak{Z}}_n}\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big), {{\mathfrak{Z}}_n} \frac{\nabla}{{\mathfrak{Z}}_n}\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big)]\\ & =[ \frac{\nabla}{{\mathfrak{Z}}_n}(\Psi-1)\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big), {\nabla}\big(\frac{f}{t_{LT}}\mathbf{e}_\delta\big) ] \\ & =[0,\partial(f) \mathbf{e}_\delta ], \end{align*} $$
whence the claim. Here, for the last equality we used the formula (iv) of Remark 3.12.
noting that
![]() $\mathcal {R}_K(\tilde {\delta })\xrightarrow {\cong }\frac {1}{t_{LT}}\mathcal {R}_K(\delta ), f\mathbf {e}_{\tilde {\delta }}\mapsto \frac {f}{t_{LT}}\mathbf {e}_{{\delta }},$
is an isomorphism of
$\mathcal {R}_K(\tilde {\delta })\xrightarrow {\cong }\frac {1}{t_{LT}}\mathcal {R}_K(\delta ), f\mathbf {e}_{\tilde {\delta }}\mapsto \frac {f}{t_{LT}}\mathbf {e}_{{\delta }},$
is an isomorphism of
![]() $(\varphi ,\Gamma _L)$
-modules and that the Hodge-Tate weight of
$(\varphi ,\Gamma _L)$
-modules and that the Hodge-Tate weight of
![]() $\omega _{\chi _{LT}^{-1}\delta } $
vanishes.
$\omega _{\chi _{LT}^{-1}\delta } $
vanishes.
Thus it remains to verify the assumption of Proposition 5.9 (1), i.e.,
![]() $\iota _m(\tilde {x})-x\in \mathbf {D}^+_{\mathrm {dif},m}(\mathcal {R}_K(\delta ))\cong t_{LT}\mathbf {D}^+_{\mathrm {dif},m}(\mathcal {R}_K(\tilde {\delta }))$
for all
$\iota _m(\tilde {x})-x\in \mathbf {D}^+_{\mathrm {dif},m}(\mathcal {R}_K(\delta ))\cong t_{LT}\mathbf {D}^+_{\mathrm {dif},m}(\mathcal {R}_K(\tilde {\delta }))$
for all
![]() $m\geq n.$
$m\geq n.$
From (107) and Remark 3.12 (iii) we obtain the equality
Using that
![]() $(1-\varphi )(f\mathbf {e}_{\tilde {\delta }})={{\mathfrak {Z}}_n}\beta $
for some
$(1-\varphi )(f\mathbf {e}_{\tilde {\delta }})={{\mathfrak {Z}}_n}\beta $
for some
![]() $\beta \in \mathcal {R}_K(\tilde {\delta })^{\Psi =0}$
by Lemma 4.4, we conclude for any
$\beta \in \mathcal {R}_K(\tilde {\delta })^{\Psi =0}$
by Lemma 4.4, we conclude for any
![]() $m\geq n+1,$
$m\geq n+1,$
 $$ \begin{align*} \iota_m\big(\frac{\nabla}{{\mathfrak{Z}}_n}( f\mathbf{e}_{\tilde{\delta}}) \big)&- \iota_{m-1}\big(\frac{\nabla}{{\mathfrak{Z}}_n}( f\mathbf{e}_{\tilde{\delta}}) \big) \\ & = \iota_m\big((1-\varphi)\frac{\nabla}{{\mathfrak{Z}}_n}( f\mathbf{e}_{\tilde{\delta}}) \big)\\ & =\iota_m\big(\frac{\nabla}{{\mathfrak{Z}}_n}( (1-\varphi) f\mathbf{e}_{\tilde{\delta}}) \big)\\ & =\iota_m\big(\frac{\nabla}{{\mathfrak{Z}}_n}( {{\mathfrak{Z}}_n}\beta) \big)=\iota_m(\nabla(\beta))\in t_{LT}\mathbf{D}^+_{\mathrm{dif},m}(\mathcal{R}_K(\tilde{\delta})) \end{align*} $$
$$ \begin{align*} \iota_m\big(\frac{\nabla}{{\mathfrak{Z}}_n}( f\mathbf{e}_{\tilde{\delta}}) \big)&- \iota_{m-1}\big(\frac{\nabla}{{\mathfrak{Z}}_n}( f\mathbf{e}_{\tilde{\delta}}) \big) \\ & = \iota_m\big((1-\varphi)\frac{\nabla}{{\mathfrak{Z}}_n}( f\mathbf{e}_{\tilde{\delta}}) \big)\\ & =\iota_m\big(\frac{\nabla}{{\mathfrak{Z}}_n}( (1-\varphi) f\mathbf{e}_{\tilde{\delta}}) \big)\\ & =\iota_m\big(\frac{\nabla}{{\mathfrak{Z}}_n}( {{\mathfrak{Z}}_n}\beta) \big)=\iota_m(\nabla(\beta))\in t_{LT}\mathbf{D}^+_{\mathrm{dif},m}(\mathcal{R}_K(\tilde{\delta})) \end{align*} $$
In particular, we obtain
for any
![]() $m\geq n$
by induction. This finishes the proof.
$m\geq n$
by induction. This finishes the proof.
By an analogous density argument (using the results from Appendix A) as in [Reference Nakamura36, Cor. 4.17] the Propositions 8.11 and 8.14 imply that
![]() $\epsilon _{K}(\mathcal {R}_K(\delta )):\mathbf {1}_{K}\xrightarrow {\cong } \Delta _K(\mathcal {R}_K(\delta ))$
satisfies conditions (iii), (iv) of Conjecture 7.6 for any analytic character
$\epsilon _{K}(\mathcal {R}_K(\delta )):\mathbf {1}_{K}\xrightarrow {\cong } \Delta _K(\mathcal {R}_K(\delta ))$
satisfies conditions (iii), (iv) of Conjecture 7.6 for any analytic character
![]() $\delta ,$
i.e., for any rank one analytic
$\delta ,$
i.e., for any rank one analytic
![]() $(\varphi ,\Gamma _L)$
-module.
$(\varphi ,\Gamma _L)$
-module.
8.5.3 Exceptional case
This subsection has been inspired by [Reference Nakamura36, 4B2] and [Reference Venjakob54, §2.5].
By observing that the character
![]() $x^0$
is dual to
$x^0$
is dual to
![]() $\chi =x|x|$
with respect to the pairing in Theorem 4.16 and upon applying compatibility with this duality 7.14 as well as with twisting according to Propositions 8.8 and 8.9 one easily reduces the verification of condition (vi) in the exceptional case, i.e.,
$\chi =x|x|$
with respect to the pairing in Theorem 4.16 and upon applying compatibility with this duality 7.14 as well as with twisting according to Propositions 8.8 and 8.9 one easily reduces the verification of condition (vi) in the exceptional case, i.e.,
![]() $\delta $
being of the form
$\delta $
being of the form
![]() $x^{-i}$
or
$x^{-i}$
or
![]() $x^i\chi =x^{i+1}|x|$
for
$x^i\chi =x^{i+1}|x|$
for
![]() $i\in \mathbb {N}$
(recall
$i\in \mathbb {N}$
(recall
![]() $0\in \mathbb {N}$
), to the case of
$0\in \mathbb {N}$
), to the case of
![]() $\delta =\chi =x|x|.$
$\delta =\chi =x|x|.$
First we are going to describe
![]() $\bar {\Theta }(\delta ).$
To this aim note that the natural inclusion
$\bar {\Theta }(\delta ).$
To this aim note that the natural inclusion
![]() $Kz^0=Pol_{\leq 0}(o_L)\hookrightarrow LA(o_L)$
, which is a splitting of the projection sending
$Kz^0=Pol_{\leq 0}(o_L)\hookrightarrow LA(o_L)$
, which is a splitting of the projection sending
![]() $\phi $
to
$\phi $
to
![]() $\phi (0),$
induces a quasi-isomorphism
$\phi (0),$
induces a quasi-isomorphism
by Lemma 4.20.
The long exact
![]() $H^i_{\Psi , D(\Gamma _L,K)}$
-sequence attached to (29) together with (84), (109) induces for dimension reasons (compare with Lemma 4.22 (v)) an isomorphism
$H^i_{\Psi , D(\Gamma _L,K)}$
-sequence attached to (29) together with (84), (109) induces for dimension reasons (compare with Lemma 4.22 (v)) an isomorphism
which - induced by the evaluation at
![]() $0$
of the Colmez transform given by (30) - sends
$0$
of the Colmez transform given by (30) - sends
![]() $[f_1\mathbf {e}_\chi ,f_2 \mathbf {e}_\chi ]$
to
$[f_1\mathbf {e}_\chi ,f_2 \mathbf {e}_\chi ]$
to
as well as
which sends
![]() $[f\mathbf {e}_\chi ]$
to
$[f\mathbf {e}_\chi ]$
to
Finally, again as part of the long exact
![]() $H^i_{\Psi , D(\Gamma _L,K)}$
-sequence attached to (29), we have an isomorphism
$H^i_{\Psi , D(\Gamma _L,K)}$
-sequence attached to (29), we have an isomorphism
 $$ \begin{align} \alpha_0: (Kz^0 \cong) H^0_{\Psi, D(\Gamma_L,K)}(Kz^0)&\cong H^1_{\Psi, D(\Gamma_L,K)}(LA(o_L))\cong H^1_{\Psi, D(\Gamma_L,K)}(\mathcal{R}_K^+(\chi))\notag\\ &\cong H^1_{ D(\Gamma_L,K)} ( H^0_{\Psi}(\mathcal{R}_K^+(\chi))). \end{align} $$
$$ \begin{align} \alpha_0: (Kz^0 \cong) H^0_{\Psi, D(\Gamma_L,K)}(Kz^0)&\cong H^1_{\Psi, D(\Gamma_L,K)}(LA(o_L))\cong H^1_{\Psi, D(\Gamma_L,K)}(\mathcal{R}_K^+(\chi))\notag\\ &\cong H^1_{ D(\Gamma_L,K)} ( H^0_{\Psi}(\mathcal{R}_K^+(\chi))). \end{align} $$
But note that in contrast to the generic case the canonical map
 $$ \begin{align} H^1_{\Psi,D(\Gamma_L,K)}(\mathcal{R}_K^+(\delta))\cong H^1_{D(\Gamma_L,K)}(H^0_\Psi(\mathcal{R}_K^+(\delta)))&\to H^1_{D(\Gamma_L,K)}(H^0_\Psi(\mathcal{R}_K^+(\delta)))\notag\\ &\hookrightarrow H^1_{\Psi,D(\Gamma_L,K)}(\mathcal{R}_K(\delta)) \end{align} $$
$$ \begin{align} H^1_{\Psi,D(\Gamma_L,K)}(\mathcal{R}_K^+(\delta))\cong H^1_{D(\Gamma_L,K)}(H^0_\Psi(\mathcal{R}_K^+(\delta)))&\to H^1_{D(\Gamma_L,K)}(H^0_\Psi(\mathcal{R}_K^+(\delta)))\notag\\ &\hookrightarrow H^1_{\Psi,D(\Gamma_L,K)}(\mathcal{R}_K(\delta)) \end{align} $$
is the zero map, which can be seen by using (83), (88) and counting dimensions. Moreover, we have
![]() $ H^0_{\Psi ,D(\Gamma _L,K)}(\mathcal {R}_K^+(\chi ))=H^0_{\Psi ,D(\Gamma _L,K)}(\mathcal {R}_K(\chi ))=0= H^1_{D(U)}(H^1_\Psi (\mathcal {R}_K^+(\delta )))=H^2_{\Psi ,D(\Gamma _L,K)}(\mathcal {R}_K^+(\chi ))$
by Lemma 4.22 (v) and (84) as well as
$ H^0_{\Psi ,D(\Gamma _L,K)}(\mathcal {R}_K^+(\chi ))=H^0_{\Psi ,D(\Gamma _L,K)}(\mathcal {R}_K(\chi ))=0= H^1_{D(U)}(H^1_\Psi (\mathcal {R}_K^+(\delta )))=H^2_{\Psi ,D(\Gamma _L,K)}(\mathcal {R}_K^+(\chi ))$
by Lemma 4.22 (v) and (84) as well as
![]() $H^0_{\Psi , D(\Gamma _L,K)}(LA(o_L))\cong H^0_{\Psi , D(\Gamma _L,K)}(Kx^0)\cong Kx^0$
(cf. (34).
$H^0_{\Psi , D(\Gamma _L,K)}(LA(o_L))\cong H^0_{\Psi , D(\Gamma _L,K)}(Kx^0)\cong Kx^0$
(cf. (34).
Altogether it follows that the isomorphism
 $$\begin{align*}\bar{\Theta}(\chi):\bigotimes_{i=0}^2 \mathbf{d}_{K[\Gamma_L/U]}(H^i_{\Psi_L,{{\mathfrak{Z}}}}(\mathcal{R}_K(\chi)))^{(-1)^{i+1}}\otimes_{K[\Gamma_L/U]}K\cong (K\mathbf{e}_\chi,1) \end{align*}$$
$$\begin{align*}\bar{\Theta}(\chi):\bigotimes_{i=0}^2 \mathbf{d}_{K[\Gamma_L/U]}(H^i_{\Psi_L,{{\mathfrak{Z}}}}(\mathcal{R}_K(\chi)))^{(-1)^{i+1}}\otimes_{K[\Gamma_L/U]}K\cong (K\mathbf{e}_\chi,1) \end{align*}$$
coincides with the composite
 $$ \begin{align} \notag \bigotimes_{i=1}^2 \mathbf{d}_{K }(H^i_{\Psi_L,D(\Gamma_L,K)}&(\mathcal{R}_K(\chi)))^{(-1)^{i+1}} \\ & \xrightarrow{\alpha} \bigotimes_{i=0}^2 \mathbf{d}_{K }(H^i_{\Psi_L,D(\Gamma_L,K)}(Kx^0))^{(-1)^{i+1}} \otimes \mathbf{d}_{K}(H^1_{D(\Gamma_L,K)}(H^0_{\Psi}(\mathcal{R}_K^+(\chi))) ) \notag\\ & \xrightarrow{\beta\otimes \operatorname{id}} \mathbf{d}_{K }(H^1_{D(\Gamma_L,K)}(H^0_{\Psi}(\mathcal{R}_K^+(\chi))) ) \xrightarrow{\varrho} (K\mathbf{e}_\chi,1), \end{align} $$
$$ \begin{align} \notag \bigotimes_{i=1}^2 \mathbf{d}_{K }(H^i_{\Psi_L,D(\Gamma_L,K)}&(\mathcal{R}_K(\chi)))^{(-1)^{i+1}} \\ & \xrightarrow{\alpha} \bigotimes_{i=0}^2 \mathbf{d}_{K }(H^i_{\Psi_L,D(\Gamma_L,K)}(Kx^0))^{(-1)^{i+1}} \otimes \mathbf{d}_{K}(H^1_{D(\Gamma_L,K)}(H^0_{\Psi}(\mathcal{R}_K^+(\chi))) ) \notag\\ & \xrightarrow{\beta\otimes \operatorname{id}} \mathbf{d}_{K }(H^1_{D(\Gamma_L,K)}(H^0_{\Psi}(\mathcal{R}_K^+(\chi))) ) \xrightarrow{\varrho} (K\mathbf{e}_\chi,1), \end{align} $$
where
![]() $\alpha $
is induced by
$\alpha $
is induced by
![]() $\alpha _i,$
for
$\alpha _i,$
for
![]() $i=0,1,2,$
and
$i=0,1,2,$
and
![]() $\beta $
is the canonical isomorphism
$\beta $
is the canonical isomorphism
 $$ \begin{align} \bigotimes_{i=0}^2 \mathbf{d}_{K }(H^i_{\Psi_L,D(\Gamma_L,K)}&(Kx^0))^{(-1)^{i+1}}\cong \mathbf{1}_{K} \end{align} $$
$$ \begin{align} \bigotimes_{i=0}^2 \mathbf{d}_{K }(H^i_{\Psi_L,D(\Gamma_L,K)}&(Kx^0))^{(-1)^{i+1}}\cong \mathbf{1}_{K} \end{align} $$
which stems from the base change of the trivialisation of
![]() $\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (LA(o_L)))$
from (i) of Lemma 8.3. Finally,
$\mathbf {d}_{D(\Gamma _L,K)}(\mathcal {T}_\Psi (LA(o_L)))$
from (i) of Lemma 8.3. Finally,
![]() $\varrho $
is induced from (94), i.e., by
$\varrho $
is induced from (94), i.e., by
-
(i)
 $H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\chi )))\cong H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\chi )^{\Psi =0})$
induced by
$H^1_{{{\mathfrak {Z}}}}(H^0_\Psi (\mathcal {R}_K^+(\chi )))\cong H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\chi )^{\Psi =0})$
induced by
 $1-\varphi ,$
and
$1-\varphi ,$
and -
(ii)
 $H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\chi )^{\Psi =0})\xrightarrow {C_{Tr}({{\mathfrak {Z}}_n})}(\mathcal {R}_K^+(\delta )^{\Psi =0})_U \cong D(\Gamma _L,K)_U\cong K[\Gamma _L/U]\mathbf {e}_\chi $
using
$H^1_{{{\mathfrak {Z}}}}(\mathcal {R}_K^+(\chi )^{\Psi =0})\xrightarrow {C_{Tr}({{\mathfrak {Z}}_n})}(\mathcal {R}_K^+(\delta )^{\Psi =0})_U \cong D(\Gamma _L,K)_U\cong K[\Gamma _L/U]\mathbf {e}_\chi $
using
 $(\mathfrak {M}_\chi \circ \sigma _{-1})^{-1}.$
$(\mathfrak {M}_\chi \circ \sigma _{-1})^{-1}.$
Consider the basis
![]() $\tilde {f}_0:=z^0, (\tilde {f}_{1,1}:=(z^0,0), \tilde {f}_{1,2}:=(0,z^0))$
and
$\tilde {f}_0:=z^0, (\tilde {f}_{1,1}:=(z^0,0), \tilde {f}_{1,2}:=(0,z^0))$
and
![]() $\tilde {f}_2=z^0$
of
$\tilde {f}_2=z^0$
of
![]() $H^0_{\Psi ,D(\Gamma _L,K)}(Kx^0), H^1_{\Psi ,D(\Gamma _L,K)}(Kx^0)$
and
$H^0_{\Psi ,D(\Gamma _L,K)}(Kx^0), H^1_{\Psi ,D(\Gamma _L,K)}(Kx^0)$
and
![]() $H^2_{\Psi ,D(\Gamma _L,K)}(Kx^0),$
respectively. Then, analogously to [Reference Nakamura36, Lem. 4.19] one easily checks that
$H^2_{\Psi ,D(\Gamma _L,K)}(Kx^0),$
respectively. Then, analogously to [Reference Nakamura36, Lem. 4.19] one easily checks that
where
![]() $\tilde {f}_i^*$
denotes the dual basis of
$\tilde {f}_i^*$
denotes the dual basis of
![]() $\tilde {f}_i$
for
$\tilde {f}_i$
for
![]() $i=0,2.$
So it remains to study the effect of
$i=0,2.$
So it remains to study the effect of
![]() $\varrho .$
$\varrho .$
In order to calculate the effect of
![]() $\alpha _0$
consider the Coleman power series
$\alpha _0$
consider the Coleman power series
![]() $g:=g_{\iota (u),u}(T)$
Footnote
27
in the notation of [Reference Schneider and Venjakob45, Theorem 2.2], where we consider
$g:=g_{\iota (u),u}(T)$
Footnote
27
in the notation of [Reference Schneider and Venjakob45, Theorem 2.2], where we consider
as an element of
![]() $\varprojlim _n L_n^\times $
, the group of units of the corresponding field of norms
$\varprojlim _n L_n^\times $
, the group of units of the corresponding field of norms
![]() $ \mathbf {E}_L$
(cf. [Reference Kisin and Ren30, Lem. 1.4]).
$ \mathbf {E}_L$
(cf. [Reference Kisin and Ren30, Lem. 1.4]).
Remark 8.15. The element
![]() $\frac {\partial g}{g}$
$\frac {\partial g}{g}$
-
(i) belongs to
 $\mathcal {R}_K^{\Psi =\frac {\pi _L}{q}}$
and
$\mathcal {R}_K^{\Psi =\frac {\pi _L}{q}}$
and -
(ii) satisfies
 $Res(\frac {\partial g}{g}dt_{LT})=1$
.
$Res(\frac {\partial g}{g}dt_{LT})=1$
.
Proof. By the last sentence of section 2 of [Reference Schneider and Venjakob45] the term
![]() $\frac {\partial g}{g}$
belongs to
$\frac {\partial g}{g}$
belongs to
![]() $\mathcal {R}_K^{\Psi =\frac {\pi _L}{q}}$
. By the explicit reciprocity law Prop. 6.3 in (loc. cit.) we obtainFootnote
28
$\mathcal {R}_K^{\Psi =\frac {\pi _L}{q}}$
. By the explicit reciprocity law Prop. 6.3 in (loc. cit.) we obtainFootnote
28
Indeed, under the reciprocity map
![]() $\mathrm {rec} _{\mathbf {E}_L} $
the inverse of the uniformiser
$\mathrm {rec} _{\mathbf {E}_L} $
the inverse of the uniformiser
![]() $\iota (u) $
is sent to the Frobenius (lift)
$\iota (u) $
is sent to the Frobenius (lift)
![]() $\varphi _q$
of
$\varphi _q$
of
![]() $\mathbf {A},$
whence the cocycle
$\mathbf {A},$
whence the cocycle
![]() $\partial _{\varphi }(1)$
, which is given by sending
$\partial _{\varphi }(1)$
, which is given by sending
![]() $h\in H$
to
$h\in H$
to
![]() $ha-a$
for some
$ha-a$
for some
![]() $a\in \mathbf {A}$
with
$a\in \mathbf {A}$
with
![]() $\varphi _q(a)-a=1,$
sends
$\varphi _q(a)-a=1,$
sends
![]() $\mathrm {rec}_{\mathbf {E}_L}(\iota (u)) $
to
$\mathrm {rec}_{\mathbf {E}_L}(\iota (u)) $
to
![]() $1$
tautologically.
$1$
tautologically.
The following Lemma should be compared to [Reference Nakamura36, Lem. 4.20] and [Reference Venjakob54, Lem. 2.9].
Lemma 8.16. The isomorphism
sends
![]() $\tilde {f}_0$
to
$\tilde {f}_0$
to
![]() $-\Omega \frac {q-1}{q}\left ({{\mathfrak {Z}}}(\log (g(T)))\right )_{|T=0}\mathbf {e}_\chi .$
$-\Omega \frac {q-1}{q}\left ({{\mathfrak {Z}}}(\log (g(T)))\right )_{|T=0}\mathbf {e}_\chi .$
Proof. By Remark 8.15 we obtain an element
![]() $\frac {\partial g}{g}\mathbf {e}_\chi \in \mathcal {R}_K(\chi )^{\Psi =1}$
which lifts
$\frac {\partial g}{g}\mathbf {e}_\chi \in \mathcal {R}_K(\chi )^{\Psi =1}$
which lifts
![]() $\tilde {f}_0$
under the Coleman transform (30). Thus
$\tilde {f}_0$
under the Coleman transform (30). Thus
![]() $\alpha _0(\tilde {f}_0)$
is represented by
$\alpha _0(\tilde {f}_0)$
is represented by
 $$\begin{align*}{{\mathfrak{Z}}}\left(\frac{\partial g}{g}\mathbf{e}_\chi \right)={{\mathfrak{Z}}}\left(\partial \log (g)\mathbf{e}_\chi \right)=\partial \left({{\mathfrak{Z}}}\log g \right)\mathbf{e}_\chi\end{align*}$$
$$\begin{align*}{{\mathfrak{Z}}}\left(\frac{\partial g}{g}\mathbf{e}_\chi \right)={{\mathfrak{Z}}}\left(\partial \log (g)\mathbf{e}_\chi \right)=\partial \left({{\mathfrak{Z}}}\log g \right)\mathbf{e}_\chi\end{align*}$$
by (90). It is mapped into
![]() $H^1_{D(\Gamma _L,K)}(\mathcal {R}_K^+(\chi )^{\Psi =0})$
to the class of
$H^1_{D(\Gamma _L,K)}(\mathcal {R}_K^+(\chi )^{\Psi =0})$
to the class of
 $$ \begin{align*} (1-\varphi){{\mathfrak{Z}}}\left(\frac{\partial g}{g}\mathbf{e}_\chi \right)&={{\mathfrak{Z}}}(1-\varphi)\left(\partial \log (g)\mathbf{e}_\chi \right)\in \mathcal{R}_K^+(\chi)^{\Psi=0}\\ &={{\mathfrak{Z}}}\left(\partial (1-\frac{\varphi}{q})(\log (g))\mathbf{e}_\chi \right)\\ &=\left(Tw_{\chi_{LT}}({{\mathfrak{Z}}})\partial (1-\frac{\varphi}{q})(\log (g))\right)\mathbf{e}_\chi \\ &=\left(\partial {{\mathfrak{Z}}}(1-\frac{\varphi}{q})(\log (g))\right)\mathbf{e}_\chi \\ &=\partial \left((1-\frac{\varphi}{q}){{\mathfrak{Z}}}(\log (g))\mathbf{e}_{|x|} \right). \end{align*} $$
$$ \begin{align*} (1-\varphi){{\mathfrak{Z}}}\left(\frac{\partial g}{g}\mathbf{e}_\chi \right)&={{\mathfrak{Z}}}(1-\varphi)\left(\partial \log (g)\mathbf{e}_\chi \right)\in \mathcal{R}_K^+(\chi)^{\Psi=0}\\ &={{\mathfrak{Z}}}\left(\partial (1-\frac{\varphi}{q})(\log (g))\mathbf{e}_\chi \right)\\ &=\left(Tw_{\chi_{LT}}({{\mathfrak{Z}}})\partial (1-\frac{\varphi}{q})(\log (g))\right)\mathbf{e}_\chi \\ &=\left(\partial {{\mathfrak{Z}}}(1-\frac{\varphi}{q})(\log (g))\right)\mathbf{e}_\chi \\ &=\partial \left((1-\frac{\varphi}{q}){{\mathfrak{Z}}}(\log (g))\mathbf{e}_{|x|} \right). \end{align*} $$
Now we use the commutative diagram

to conclude by observing that the evaluation at
![]() $\mathbf {1}$
corresponds to setting
$\mathbf {1}$
corresponds to setting
![]() $T=0$
and that
$T=0$
and that
![]() $\left ((1-\frac {\varphi }{q}){{\mathfrak {Z}}}(\log (g(T)))\right )_{|T=0}=\frac {q-1}{q}\left ({{\mathfrak {Z}}}(\log (g(T)))\right )_{|T=0}$
.
$\left ((1-\frac {\varphi }{q}){{\mathfrak {Z}}}(\log (g(T)))\right )_{|T=0}=\frac {q-1}{q}\left ({{\mathfrak {Z}}}(\log (g(T)))\right )_{|T=0}$
.
Remark 8.17. The map
![]() $v\mapsto (1-\frac {\varphi }{q})(\log (g_{v,u}(T)))$
generalizes Coleman’s map as used in Kato’s proof of the classical rank one case, cf. [Reference Venjakob54, (2.5)].
$v\mapsto (1-\frac {\varphi }{q})(\log (g_{v,u}(T)))$
generalizes Coleman’s map as used in Kato’s proof of the classical rank one case, cf. [Reference Venjakob54, (2.5)].
Lemma 8.18. With the notation in the proof of Lemma 8.16 we have
Proof. Note that
![]() $g\in To_L[[T]].$
Writing
$g\in To_L[[T]].$
Writing
![]() $g=\sum _{i\geq 1} a_iT^i$
we see that for any
$g=\sum _{i\geq 1} a_iT^i$
we see that for any
![]() $\gamma \in \Gamma _n$
we have
$\gamma \in \Gamma _n$
we have
 $$ \begin{align*} ((\gamma-1)\log(g(T)))_{|T=0} &=\log(\frac{g([\chi_{LT}(\gamma)](T))}{g(T)})_{|T=0} \\ &=\log(\left(\frac{\sum_{i\geq 1}a_i\frac{([\chi_{LT}(\gamma)](T))^i}{T}}{\sum_{i\geq 1} a_iT^{i-1}}\right)_{|T=0} )\\ &=\log(\frac{ a_1 \chi_{LT}(\gamma) }{ a_1 } ) =\log( \chi_{LT}(\gamma) ). \end{align*} $$
$$ \begin{align*} ((\gamma-1)\log(g(T)))_{|T=0} &=\log(\frac{g([\chi_{LT}(\gamma)](T))}{g(T)})_{|T=0} \\ &=\log(\left(\frac{\sum_{i\geq 1}a_i\frac{([\chi_{LT}(\gamma)](T))^i}{T}}{\sum_{i\geq 1} a_iT^{i-1}}\right)_{|T=0} )\\ &=\log(\frac{ a_1 \chi_{LT}(\gamma) }{ a_1 } ) =\log( \chi_{LT}(\gamma) ). \end{align*} $$
It follows that for elements
![]() $\lambda =\sum _i a_i(\gamma _i-1)$
in the K-span S of
$\lambda =\sum _i a_i(\gamma _i-1)$
in the K-span S of
![]() $\gamma -1, \gamma \in \Gamma _n\setminus {\{1\}}$
, in
$\gamma -1, \gamma \in \Gamma _n\setminus {\{1\}}$
, in
![]() $D(\Gamma _n,K)$
we have
$D(\Gamma _n,K)$
we have
because
![]() $\sum _i a_i(\gamma _i-1)=\sum _i a_i\gamma _i - (\sum _i a_i)1$
and
$\sum _i a_i(\gamma _i-1)=\sum _i a_i\gamma _i - (\sum _i a_i)1$
and
![]() $\log (\chi _{LT}(1))=0.$
Since
$\log (\chi _{LT}(1))=0.$
Since
![]() ${{\mathfrak {Z}}}_n$
belongs to the closure of S the claim follows by continuity.
${{\mathfrak {Z}}}_n$
belongs to the closure of S the claim follows by continuity.
Now we define a basis
![]() $(f_{1,1},f_{1,2})$
of
$(f_{1,1},f_{1,2})$
of
![]() $ H^1_{\Psi _L,D(\Gamma _L,K)}(\mathcal {R}_K(\chi )) $
and
$ H^1_{\Psi _L,D(\Gamma _L,K)}(\mathcal {R}_K(\chi )) $
and
![]() $f_2$
of
$f_2$
of
![]() $H^2_{\Psi _L,D(\Gamma _L,K)}(\mathcal {R}_K(\chi )) $
viaFootnote
29
$H^2_{\Psi _L,D(\Gamma _L,K)}(\mathcal {R}_K(\chi )) $
viaFootnote
29
Combining (116), (118) and (120) with Lemmata 8.16, 8.18 we obtain
Corollary 8.19.
![]() $\bar {\Theta }(\chi )((f_{1,1}\wedge f_{1,2})\otimes f_2^*)= -\Omega \frac {q-1}{q}C_g({{\mathfrak {Z}}}_n)C_{Tr}({{\mathfrak {Z}}}_n)\mathbf {e}_\chi =-\Omega \ \mathbf {e}_\chi .$
$\bar {\Theta }(\chi )((f_{1,1}\wedge f_{1,2})\otimes f_2^*)= -\Omega \frac {q-1}{q}C_g({{\mathfrak {Z}}}_n)C_{Tr}({{\mathfrak {Z}}}_n)\mathbf {e}_\chi =-\Omega \ \mathbf {e}_\chi .$
Now we shall compare this to the de Rham
![]() $\epsilon $
-isomorphism, i.e., mainly to the map
$\epsilon $
-isomorphism, i.e., mainly to the map
![]() $\Theta (\mathcal {R}_K(\chi ))$
, because
$\Theta (\mathcal {R}_K(\chi ))$
, because
and
![]() $\Theta _{F,dR,u}(\mathcal {R}_F(\chi )): \mathbf {d}_K( \mathbf {D}_{\text {dR}}(\mathcal {R}(\chi )) ) \xrightarrow {\cong }\Delta _{K,2}(\mathcal {R}_K(\chi ))$
corresponds to the isomorphism
$\Theta _{F,dR,u}(\mathcal {R}_F(\chi )): \mathbf {d}_K( \mathbf {D}_{\text {dR}}(\mathcal {R}(\chi )) ) \xrightarrow {\cong }\Delta _{K,2}(\mathcal {R}_K(\chi ))$
corresponds to the isomorphism
as
![]() $\tilde {\varepsilon }(\mathcal {R}_K(\chi ),u)=1$
due to
$\tilde {\varepsilon }(\mathcal {R}_K(\chi ),u)=1$
due to
![]() $\chi $
being crystalline.
$\chi $
being crystalline.
By the long exact sequence (66) the map
![]() $\Theta (\mathcal {R}_K(\chi ))$
is induced from the following isomorphisms and exact sequences
$\Theta (\mathcal {R}_K(\chi ))$
is induced from the following isomorphisms and exact sequences
(with
![]() $\Upsilon ^{\prime }_f$
induced by
$\Upsilon ^{\prime }_f$
induced by
![]() $\Upsilon '$
in Remark 4.18)
$\Upsilon '$
in Remark 4.18)
 $$ \begin{align} H^{1}_{\Psi,{\mathfrak{Z}}_n}(\mathcal{R}_K(\chi))^{\Gamma_L}/H^{1}_{\Psi,{\mathfrak{Z}}_n}(\mathcal{R}_K(\chi))^{\Gamma_L}_f&\xrightarrow{\bar{x}\mapsto \{y\mapsto \langle(\Upsilon')^{-1}(x),y\rangle_{\mathcal{R}(\chi)}\} }(H^{1}_{\varphi,{\mathfrak{Z}}_n}(\mathcal{R}_K)^{\Gamma_L}_f)^*\notag\\ &\xrightarrow{(\exp_{f,\mathcal{R}_K})^*}\mathbf{D}_{\text{cris}}(\mathcal{R}_K)^{*} \end{align} $$
$$ \begin{align} H^{1}_{\Psi,{\mathfrak{Z}}_n}(\mathcal{R}_K(\chi))^{\Gamma_L}/H^{1}_{\Psi,{\mathfrak{Z}}_n}(\mathcal{R}_K(\chi))^{\Gamma_L}_f&\xrightarrow{\bar{x}\mapsto \{y\mapsto \langle(\Upsilon')^{-1}(x),y\rangle_{\mathcal{R}(\chi)}\} }(H^{1}_{\varphi,{\mathfrak{Z}}_n}(\mathcal{R}_K)^{\Gamma_L}_f)^*\notag\\ &\xrightarrow{(\exp_{f,\mathcal{R}_K})^*}\mathbf{D}_{\text{cris}}(\mathcal{R}_K)^{*} \end{align} $$
and
which is dual to the natural isomorphism
![]() $H^{0}_{\varphi ,{\mathfrak {Z}}_n}(\mathcal {R}_K)^{\Gamma _L} \cong \mathbf {D}_{\text {cris}}(\mathcal {R}_K), 1\mapsto d_0:=1\in K=\mathbf {D}_{\text {cris}}(\mathcal {R}_K).$
We define basis
$H^{0}_{\varphi ,{\mathfrak {Z}}_n}(\mathcal {R}_K)^{\Gamma _L} \cong \mathbf {D}_{\text {cris}}(\mathcal {R}_K), 1\mapsto d_0:=1\in K=\mathbf {D}_{\text {cris}}(\mathcal {R}_K).$
We define basis
![]() $e_0$
and
$e_0$
and
![]() $(e_{1,1},e_{1,2})$
of
$(e_{1,1},e_{1,2})$
of
![]() $H^{0}_{\varphi ,{\mathfrak {Z}}_n}(\mathcal {R}_K)^{\Gamma _L} $
and
$H^{0}_{\varphi ,{\mathfrak {Z}}_n}(\mathcal {R}_K)^{\Gamma _L} $
and
![]() $H^{1}_{\varphi ,{\mathfrak {Z}}_n}(\mathcal {R}_K)^{\Gamma _L},$
respectively, as follows:Footnote
30
$H^{1}_{\varphi ,{\mathfrak {Z}}_n}(\mathcal {R}_K)^{\Gamma _L},$
respectively, as follows:Footnote
30
Lemma 8.20.
-
(i)
 $\exp _{f,\mathcal {R}_K}(d_0)=e_{1,1}$
$\exp _{f,\mathcal {R}_K}(d_0)=e_{1,1}$
-
(ii)
 $ \Upsilon ^{\prime }_f\circ \exp _{\mathcal {R}_K(\chi )}(t_{LT}^{-1}\mathbf {e}_\chi )=\frac {q-1}{q}f_{1,1}$
$ \Upsilon ^{\prime }_f\circ \exp _{\mathcal {R}_K(\chi )}(t_{LT}^{-1}\mathbf {e}_\chi )=\frac {q-1}{q}f_{1,1}$
-
(iii) Using the pairing
from Remark 4.18 we have $$ \begin{align*}\{\!\!\{-,-\}\!\!\}_{\mathcal{R}_K(\chi)}\colon H^i_{\Psi,{\mathfrak{Z}}_n}(\mathcal{R}_K(\chi))\times H^{2-i}_{\varphi,{\mathfrak{Z}}_n}(\mathcal{R}_K) \to K\end{align*} $$
$$ \begin{align*}\{\!\!\{-,-\}\!\!\}_{\mathcal{R}_K(\chi)}\colon H^i_{\Psi,{\mathfrak{Z}}_n}(\mathcal{R}_K(\chi))\times H^{2-i}_{\varphi,{\mathfrak{Z}}_n}(\mathcal{R}_K) \to K\end{align*} $$
 $$ \begin{align*} \{\!\!\{ f_{1,2},e_{1,1}\}\!\!\}_{\mathcal{R}_K(\chi)}=1, & \phantom{m}\{\!\!\{ f_{1,1},e_{1,1}\}\!\!\}_{\mathcal{R}_K(\chi)}=0,\\ \{\!\!\{ f_{1,2},e_{1,2}\}\!\!\}_{\mathcal{R}_K(\chi)}=0, & \phantom{m} \{\!\!\{ f_{1,1},e_{1,2}\}\!\!\}_{\mathcal{R}_K(\chi)}=1,\\ \{\!\!\{ f_2,e_0\}\!\!\}_{\mathcal{R}_K(\chi)}= -1 .& \end{align*} $$
$$ \begin{align*} \{\!\!\{ f_{1,2},e_{1,1}\}\!\!\}_{\mathcal{R}_K(\chi)}=1, & \phantom{m}\{\!\!\{ f_{1,1},e_{1,1}\}\!\!\}_{\mathcal{R}_K(\chi)}=0,\\ \{\!\!\{ f_{1,2},e_{1,2}\}\!\!\}_{\mathcal{R}_K(\chi)}=0, & \phantom{m} \{\!\!\{ f_{1,1},e_{1,2}\}\!\!\}_{\mathcal{R}_K(\chi)}=1,\\ \{\!\!\{ f_2,e_0\}\!\!\}_{\mathcal{R}_K(\chi)}= -1 .& \end{align*} $$
-
(iv)
 $(\exp _{f,\mathcal {R}_K})^*(\langle (\Upsilon ')^{-1}(f_{1,2}),-\rangle _{\mathcal {R}(\chi )})=d_0^*\in \mathbf {D}_{\text {cris}}(\mathcal {R}_K)^{*}$
, where the pairing
$(\exp _{f,\mathcal {R}_K})^*(\langle (\Upsilon ')^{-1}(f_{1,2}),-\rangle _{\mathcal {R}(\chi )})=d_0^*\in \mathbf {D}_{\text {cris}}(\mathcal {R}_K)^{*}$
, where the pairing
 $\langle -,-\rangle _{\mathcal {R}(\chi )}$
had been introduced in Theorem 4.16.
$\langle -,-\rangle _{\mathcal {R}(\chi )}$
had been introduced in Theorem 4.16.
Proof. (i) follows from Proposition 5.9(ii) by taking
![]() $\tilde {x}=1.$
For (ii) we apply Proposition 5.9 (i) with
$\tilde {x}=1.$
For (ii) we apply Proposition 5.9 (i) with
![]() $\tilde {x}=\frac {f}{t_{LT}}\mathbf {e}_\chi \in \mathcal {R}_K(\chi )[\frac {1}{t_{LT}}]$
, where f lies in
$\tilde {x}=\frac {f}{t_{LT}}\mathbf {e}_\chi \in \mathcal {R}_K(\chi )[\frac {1}{t_{LT}}]$
, where f lies in
![]() $\mathcal {R}_K^+$
such that
$\mathcal {R}_K^+$
such that
![]() $f(u_n)=\frac {1}{\pi _L^n}$
for any
$f(u_n)=\frac {1}{\pi _L^n}$
for any
![]() $n\geq 0.$
The existence of such f follows from the analogue of (42) over the ring
$n\geq 0.$
The existence of such f follows from the analogue of (42) over the ring
![]() $\mathcal {R}_K^+$
$\mathcal {R}_K^+$
Moreover,
![]() $\tilde {x}$
satisfies
$\tilde {x}$
satisfies
for all
![]() $n\geq 1,$
because
$n\geq 1,$
because
by Remark 3.14. Therefore the conditions of Proposition 5.9(i) are satisfied and hence we conclude that
and
Hence it suffices to show that
 $$ \begin{align} Res\left(\frac{{{\mathfrak{Z}}}_nf}{t_{LT}}d\log_{LT}\right)=0 \end{align} $$
$$ \begin{align} Res\left(\frac{{{\mathfrak{Z}}}_nf}{t_{LT}}d\log_{LT}\right)=0 \end{align} $$
and
 $$ \begin{align} Res_Z\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}d\log_{LT}\right) & = -\frac{q-1}{q}, \end{align} $$
$$ \begin{align} Res_Z\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}d\log_{LT}\right) & = -\frac{q-1}{q}, \end{align} $$
because
 $-\Psi (\varphi -1)(\frac {f}{t_{LT}}\mathbf {e}_\chi )=-\frac {q}{\pi _L}\Psi \bigg (\frac {(\frac {\varphi }{q}-1)f}{t_{LT}}\bigg )\mathbf {e}_\chi $
and
$-\Psi (\varphi -1)(\frac {f}{t_{LT}}\mathbf {e}_\chi )=-\frac {q}{\pi _L}\Psi \bigg (\frac {(\frac {\varphi }{q}-1)f}{t_{LT}}\bigg )\mathbf {e}_\chi $
and
 $$ \begin{align*} Res_Z\left(\Psi\bigg(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}\bigg)d\log_{LT}\right)=\frac{\pi_L}{q}Res_Z\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}d\log_{LT}\right) \end{align*} $$
$$ \begin{align*} Res_Z\left(\Psi\bigg(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}\bigg)d\log_{LT}\right)=\frac{\pi_L}{q}Res_Z\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}d\log_{LT}\right) \end{align*} $$
by [Reference Schneider and Venjakob46, Lem. 4.5.1 (iv)]. For (127) one shows first the analogous statement for
![]() $\gamma -1$
,
$\gamma -1$
,
![]() $ \gamma \in \Gamma _L$
, instead of
$ \gamma \in \Gamma _L$
, instead of
![]() ${{\mathfrak {Z}}}_n$
by similar arguments and then concludes by continuity. For (128) we calculate
${{\mathfrak {Z}}}_n$
by similar arguments and then concludes by continuity. For (128) we calculate
 $$ \begin{align*} Res_Z\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}d\log_{LT}\right) & = Res_{t_{LT}}\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}dt_{LT}\right) \\ &= Res_{t_{LT}}\left(\frac{\frac{\varphi}{q}(f)}{t_{LT}}dt_{LT}\right)-Res_{t_{LT}}\left(\frac{ f}{t_{LT}}dt_{LT}\right) \\ &= \left(\frac{\varphi(f)}{q} \right)_{|t_{LT}=0}- \left( f \right)_{|t_{LT}=0} \\ &= \left(\frac{\varphi(f)}{q} \right)_{|Z=0}- \left( f \right)_{|Z=0} \\ & = \frac{1-q}{q}f(0)=-\frac{q-1}{q}, \end{align*} $$
$$ \begin{align*} Res_Z\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}d\log_{LT}\right) & = Res_{t_{LT}}\left(\frac{(\frac{\varphi}{q}-1)f}{t_{LT}}dt_{LT}\right) \\ &= Res_{t_{LT}}\left(\frac{\frac{\varphi}{q}(f)}{t_{LT}}dt_{LT}\right)-Res_{t_{LT}}\left(\frac{ f}{t_{LT}}dt_{LT}\right) \\ &= \left(\frac{\varphi(f)}{q} \right)_{|t_{LT}=0}- \left( f \right)_{|t_{LT}=0} \\ &= \left(\frac{\varphi(f)}{q} \right)_{|Z=0}- \left( f \right)_{|Z=0} \\ & = \frac{1-q}{q}f(0)=-\frac{q-1}{q}, \end{align*} $$
where for the first equation the reasoning is as follows: since
![]() $f(0)\neq 0$
the expression on the left-hand side has a simple pole at
$f(0)\neq 0$
the expression on the left-hand side has a simple pole at
![]() $Z=0.$
The residue formula for simple poles gives us
$Z=0.$
The residue formula for simple poles gives us
![]() $Res_Z\left (\frac {(\frac {\varphi }{q}-1)f}{t_{LT}}g_{LT}dZ \right )= \left (\frac {(\frac {\varphi }{q}-1)f(Z)}{g_{LT}(Z)}g_{LT}(Z)\right )_{\mid Z=0} = Res_{t_{LT}}\left (\frac {(\frac {\varphi }{q}-1)f}{t_{LT}}dt_{LT}\right )$
.
$Res_Z\left (\frac {(\frac {\varphi }{q}-1)f}{t_{LT}}g_{LT}dZ \right )= \left (\frac {(\frac {\varphi }{q}-1)f(Z)}{g_{LT}(Z)}g_{LT}(Z)\right )_{\mid Z=0} = Res_{t_{LT}}\left (\frac {(\frac {\varphi }{q}-1)f}{t_{LT}}dt_{LT}\right )$
.
(iii) follows by direct computation using the formulae of Remark 4.18:
upon noting that
![]() $f_{1,2}= [(0, \frac {\partial g}{g}\mathbf {e}_\chi )]$
by the proof and with notation of Lemma 8.16.
$f_{1,2}= [(0, \frac {\partial g}{g}\mathbf {e}_\chi )]$
by the proof and with notation of Lemma 8.16.
Take
![]() $f_{1,1}=[(\lambda _1\mathbf {e}_\chi ,\lambda _2 \mathbf {e}_\chi )]$
. Then
$f_{1,1}=[(\lambda _1\mathbf {e}_\chi ,\lambda _2 \mathbf {e}_\chi )]$
. Then
and, for
![]() $\lambda $
satisfying
$\lambda $
satisfying
![]() $[-1]({{\mathfrak {Z}}_n})={\mathfrak {Z}}_n^\iota =\lambda {\mathfrak {Z}}_n$
,
$[-1]({{\mathfrak {Z}}_n})={\mathfrak {Z}}_n^\iota =\lambda {\mathfrak {Z}}_n$
,
by definition of
![]() $f_{1,1}.$
Finally, writing
$f_{1,1}.$
Finally, writing
![]() $f_2=\lambda _3 \mathbf {e}_\chi $
we have
$f_2=\lambda _3 \mathbf {e}_\chi $
we have
(iv) follows from (i) and (iii) using (28), i.e.,
![]() $\langle (\Upsilon ')^{-1}(f_{1,2}),-\rangle _{\mathcal {R}(\chi )} =\{\!\!\{ f_{1,2},- \}\!\!\}_{\mathcal {R}_K(\chi )}$
.
$\langle (\Upsilon ')^{-1}(f_{1,2}),-\rangle _{\mathcal {R}(\chi )} =\{\!\!\{ f_{1,2},- \}\!\!\}_{\mathcal {R}_K(\chi )}$
.
Combining the previous lemma with (123), (124), (125), (126) we obtain
Corollary 8.21.
![]() $\Theta (\mathcal {R}_K(\chi ))((f_{1,1}\wedge f_{1,2})\otimes f_2^*)= -\frac {1}{ t_{LT}}\mathbf {e}_\chi \in K \frac {1}{ t_{LT}}\mathbf {e}_\chi =\mathbf {D}^{}_{\text {dR}}({\mathcal {R}_K(\chi )}) $
.
$\Theta (\mathcal {R}_K(\chi ))((f_{1,1}\wedge f_{1,2})\otimes f_2^*)= -\frac {1}{ t_{LT}}\mathbf {e}_\chi \in K \frac {1}{ t_{LT}}\mathbf {e}_\chi =\mathbf {D}^{}_{\text {dR}}({\mathcal {R}_K(\chi )}) $
.
Together with Corollary 8.19 and (121),(122) this proves property (vi) for the exceptional case.
Appendix A Density Argument
When verifying that
![]() $\varepsilon _{K,u}(M)$
satisfies a given property we frequently require a density argument. This is formally justified as follows: We reinterpret a given property as a commutative diagram in the category of graded line bundles (hence involving only isomorphisms). E.g. for the property (iii) of Conjecture 7.6 one takes the diagram
$\varepsilon _{K,u}(M)$
satisfies a given property we frequently require a density argument. This is formally justified as follows: We reinterpret a given property as a commutative diagram in the category of graded line bundles (hence involving only isomorphisms). E.g. for the property (iii) of Conjecture 7.6 one takes the diagram

The commutativity of this diagram for a given property P can be reinterpreted as the automorphism
![]() $P(M)$
of
$P(M)$
of
![]() $\mathbf {1}_K,$
which is obtained by going around the diagram, taking the constant value
$\mathbf {1}_K,$
which is obtained by going around the diagram, taking the constant value
![]() $1.$
In this section we will construct a (reduced) rigid analytic space
$1.$
In this section we will construct a (reduced) rigid analytic space
![]() $\mathcal {T}_{an}$
over the normal hull E of
$\mathcal {T}_{an}$
over the normal hull E of
![]() $L,$
whose
$L,$
whose
![]() $K'$
-points parameterise L-analytic
$K'$
-points parameterise L-analytic
![]() $(\varphi _L,\Gamma _L)$
-modules attached to characters
$(\varphi _L,\Gamma _L)$
-modules attached to characters
![]() $\delta \colon L \to K^{\prime \times }$
such that the map
$\delta \colon L \to K^{\prime \times }$
such that the map
![]() $M \mapsto P(M)$
is a map of rigid analytic spaces
$M \mapsto P(M)$
is a map of rigid analytic spaces
This is the same thing as a a global section of
![]() $\mathcal {O}_{\mathcal {T}_{an}}^{\times }.$
Since
$\mathcal {O}_{\mathcal {T}_{an}}^{\times }.$
Since
![]() $\mathcal {T}_{an}$
is reduced the vanishing of a global section (in our case
$\mathcal {T}_{an}$
is reduced the vanishing of a global section (in our case
![]() $M\mapsto P(M)-1$
) can be checked on a Zariski dense subset (essentially by definition as we will see below). Let
$M\mapsto P(M)-1$
) can be checked on a Zariski dense subset (essentially by definition as we will see below). Let
![]() $\mathcal {W}$
(resp.
$\mathcal {W}$
(resp.
![]() $\mathcal {T}$
) be the rigid spaces representing the functors
$\mathcal {T}$
) be the rigid spaces representing the functors
resp.
For the representability of the first functor see [Reference Buzzard10, Lemma 2]. The representability of the second functor can be seen by fixing a uniformiser, which provides us with an isomorphism
![]() $\mathcal {T} \cong \mathbb {G}_m \times \mathcal {W}$
and we denote by
$\mathcal {T} \cong \mathbb {G}_m \times \mathcal {W}$
and we denote by
![]() $\mathcal {W}_{an}$
the subspace of locally L-analytic characters inside
$\mathcal {W}_{an}$
the subspace of locally L-analytic characters inside
![]() $\mathcal {W},$
where by convention we call a character locally analytic if the composite with the restriction map to
$\mathcal {W},$
where by convention we call a character locally analytic if the composite with the restriction map to
![]() $\mathcal {O}(Y)$
is L-analytic for any affinoid
$\mathcal {O}(Y)$
is L-analytic for any affinoid
![]() $Y \subset X$
(this makes sense because
$Y \subset X$
(this makes sense because
![]() $\mathcal {O}(Y)$
is a Banach space). Similarly we define
$\mathcal {O}(Y)$
is a Banach space). Similarly we define
![]() $\mathcal {T}_{an}.$
Since
$\mathcal {T}_{an}.$
Since
![]() $o_L^\times $
is open in
$o_L^\times $
is open in
![]() $L^\times $
, we conclude that a character
$L^\times $
, we conclude that a character
![]() $\delta \in \mathcal {T}$
is L-analytic if and only if its projection to
$\delta \in \mathcal {T}$
is L-analytic if and only if its projection to
![]() $\mathcal {W}$
is L-analytic. Analogously we get an isomorphism (depending on the choice of uniformiser)
$\mathcal {W}$
is L-analytic. Analogously we get an isomorphism (depending on the choice of uniformiser)
![]() $ \mathcal {T}_{an} \cong \mathbb {G}_m \times \mathcal {W}_{an}.$
The representability of
$ \mathcal {T}_{an} \cong \mathbb {G}_m \times \mathcal {W}_{an}.$
The representability of
![]() $\mathcal {W}_{an}$
is shown in [Reference Emerton19, Proposition 6.4.5]. Recall that a character is locally L-analytic if and only if its differential at
$\mathcal {W}_{an}$
is shown in [Reference Emerton19, Proposition 6.4.5]. Recall that a character is locally L-analytic if and only if its differential at
![]() $1$
is L-linear. A character
$1$
is L-linear. A character
![]() $\delta \colon o_L^\times \to \Gamma (X,\mathcal {O}_X^\times )$
(with X affinoid over a Galois closure E of L) can be written (locally around
$\delta \colon o_L^\times \to \Gamma (X,\mathcal {O}_X^\times )$
(with X affinoid over a Galois closure E of L) can be written (locally around
![]() $1$
) as
$1$
) as
with some
![]() $a_{\mathbf {n}} \in \Gamma (X,\mathcal {O}_X),$
where
$a_{\mathbf {n}} \in \Gamma (X,\mathcal {O}_X),$
where
![]() $\Sigma $
is the set of
$\Sigma $
is the set of
![]() $\mathbb {Q}_p$
-homomorphisms
$\mathbb {Q}_p$
-homomorphisms
![]() $\sigma \colon L \to E$
and
$\sigma \colon L \to E$
and
![]() $(x-1)^{\mathbf {n}}$
is defined as
$(x-1)^{\mathbf {n}}$
is defined as
![]() $\prod _{\sigma \in \Sigma } \sigma (x-1)^{n_\sigma }$
where
$\prod _{\sigma \in \Sigma } \sigma (x-1)^{n_\sigma }$
where
![]() $\mathbf {n} = (n_{\sigma })_{\sigma }.$
The partial derivative at
$\mathbf {n} = (n_{\sigma })_{\sigma }.$
The partial derivative at
![]() $x=1$
in the direction of
$x=1$
in the direction of
![]() $\sigma \in \Sigma $
, i.e., the coefficient
$\sigma \in \Sigma $
, i.e., the coefficient
![]() $a_{e_\sigma }$
of the power series at the
$a_{e_\sigma }$
of the power series at the
![]() $\sigma $
-unit-vector is called the
$\sigma $
-unit-vector is called the
![]() $\sigma $
-part of the generalised Hodge-Tate weight of
$\sigma $
-part of the generalised Hodge-Tate weight of
![]() $\delta .$
$\delta .$
Remark A.1. A character
![]() $\delta \in \mathcal {W}$
is L-analytic if and only if
$\delta \in \mathcal {W}$
is L-analytic if and only if
![]() $a_{e_\sigma }=0$
for every
$a_{e_\sigma }=0$
for every
![]() $\sigma \neq \operatorname {id}.$
$\sigma \neq \operatorname {id}.$
Proof. This is essentially [Reference Berger5, Remark 2.7]. Note that a character is L-analytic if and only if
![]() $1$
is an L-analytic vector for the corresponding representation. (Loc. cit.) uses the logarithm as a chart around
$1$
is an L-analytic vector for the corresponding representation. (Loc. cit.) uses the logarithm as a chart around
![]() $1 \in o_L^\times $
rather than the map
$1 \in o_L^\times $
rather than the map
![]() $x \mapsto x-1.$
Since
$x \mapsto x-1.$
Since
![]() $\log _{\mathbb {G}_m}(T) = T + \dots $
the coefficients in total degree
$\log _{\mathbb {G}_m}(T) = T + \dots $
the coefficients in total degree
![]() $1$
are unaffected by the change of charts. This means that our
$1$
are unaffected by the change of charts. This means that our
![]() $a_{e_{\sigma }}$
agrees with
$a_{e_{\sigma }}$
agrees with
![]() $\nabla _{\sigma }(1)$
in (loc. cit.).
$\nabla _{\sigma }(1)$
in (loc. cit.).
Recall (cf. [Reference Bellaïche and Chenevier1, Chapter 3]) that a subset Z of a rigid analytic space X is called Zariski-dense if the only reduced analytic subset containing Z is
![]() $X_{red}.$
For a reduced Stein space this is equivalent to requiring that an analytic function vanishing along Z is identically zero. An illustrating example is the set
$X_{red}.$
For a reduced Stein space this is equivalent to requiring that an analytic function vanishing along Z is identically zero. An illustrating example is the set
![]() $p\mathbb {N} \subset \mathbb {B}^{[0,1)}.$
It is Zariski dense because a function vanishing on
$p\mathbb {N} \subset \mathbb {B}^{[0,1)}.$
It is Zariski dense because a function vanishing on
![]() $p\mathbb {N}$
has infinitely many zeroes inside the affinoids
$p\mathbb {N}$
has infinitely many zeroes inside the affinoids
![]() $\mathbb {B}^{[0,r]}$
and thus vanishes identically along an admissible cover. For
$\mathbb {B}^{[0,r]}$
and thus vanishes identically along an admissible cover. For
![]() $n\gg 0 $
the group
$n\gg 0 $
the group
![]() $U=\Gamma _n$
of n-units is an open subgroup of
$U=\Gamma _n$
of n-units is an open subgroup of
![]() $o_L^\times $
isomorphic to
$o_L^\times $
isomorphic to
![]() $o_L.$
Recall that by [Reference Schneider and Teitelbaum42] the corresponding character variety
$o_L.$
Recall that by [Reference Schneider and Teitelbaum42] the corresponding character variety
![]() $\mathfrak {X}:=\mathfrak {X}_{\Gamma _n}$
is a smooth one-dimensional quasi-Stein space. For such spaces it is known (cf. [Reference Berger, Schneider and Xie7, Section 1.1]) that the divisor of an analytic function has finite support in every affinoid subdomain and a similar argument as before shows, that a set having infinite intersection with infinitely many members of a given increasing family of affinoids
$\mathfrak {X}:=\mathfrak {X}_{\Gamma _n}$
is a smooth one-dimensional quasi-Stein space. For such spaces it is known (cf. [Reference Berger, Schneider and Xie7, Section 1.1]) that the divisor of an analytic function has finite support in every affinoid subdomain and a similar argument as before shows, that a set having infinite intersection with infinitely many members of a given increasing family of affinoids
![]() $(\mathfrak {X}_m)_{m \in \mathbb {N}}$
covering
$(\mathfrak {X}_m)_{m \in \mathbb {N}}$
covering
![]() $\mathfrak {X}$
is automatically Zariski dense. Note that we have a canonical restriction map
$\mathfrak {X}$
is automatically Zariski dense. Note that we have a canonical restriction map
which is finite and flat.
Theorem A.2. If
![]() $e <p-1$
then the set
$e <p-1$
then the set
![]() $W_{int}=\{ x^d \mid d \in \mathbb {N}\}$
is Zariski dense in
$W_{int}=\{ x^d \mid d \in \mathbb {N}\}$
is Zariski dense in
![]() $\mathcal {W}_{an}.$
If
$\mathcal {W}_{an}.$
If
![]() $e \geq p-1$
we have that the set
$e \geq p-1$
we have that the set
![]() $\{ \chi \in \mathcal {W}_{an} \mid \chi _{\mid U}=x^d \}$
is Zariski dense in
$\{ \chi \in \mathcal {W}_{an} \mid \chi _{\mid U}=x^d \}$
is Zariski dense in
![]() $\mathcal {W}_{an}.$
$\mathcal {W}_{an}.$
Proof. We first consider the restriction of
![]() $x^d$
to the subgroup
$x^d$
to the subgroup
![]() $\Gamma _n$
as above. Recall that
$\Gamma _n$
as above. Recall that
![]() $\mathfrak {X}$
is covered by the neighbourhoods
$\mathfrak {X}$
is covered by the neighbourhoods
![]() $\mathfrak {X}(r)$
consisting of characters taking values inside the disc
$\mathfrak {X}(r)$
consisting of characters taking values inside the disc
![]() $|z-1|\leq r$
Using the fact that for any element of
$|z-1|\leq r$
Using the fact that for any element of
![]() $x \in o_L^\times $
we know that
$x \in o_L^\times $
we know that
![]() $x^{q-1}$
is a
$x^{q-1}$
is a
![]() $1$
-unit and
$1$
-unit and
![]() $x^{(q-1)p^N}$
for
$x^{(q-1)p^N}$
for
![]() $N \gg 0$
is close to
$N \gg 0$
is close to
![]() $1$
we conclude that
$1$
we conclude that
![]() $x^{(q-1)p^m}$
for
$x^{(q-1)p^m}$
for
![]() $m \geq N$
are an infinite family of distinct points inside
$m \geq N$
are an infinite family of distinct points inside
![]() $\mathfrak {X}(r)$
for
$\mathfrak {X}(r)$
for
![]() $N \gg 0.$
If
$N \gg 0.$
If
![]() $e(L/\mathbb {Q}_p)<p-1$
we can decompose
$e(L/\mathbb {Q}_p)<p-1$
we can decompose
![]() $o_L^\times \cong \kappa ^\times \times (1+\pi _Lo_L).$
This allows us to cover
$o_L^\times \cong \kappa ^\times \times (1+\pi _Lo_L).$
This allows us to cover
![]() $\mathcal {W}_{an}$
by sets of the form
$\mathcal {W}_{an}$
by sets of the form
![]() $\omega ^j\mathfrak {X}(r),$
with
$\omega ^j\mathfrak {X}(r),$
with
![]() $\omega $
the composition of the projection mod
$\omega $
the composition of the projection mod
![]() $\pi $
and the Teichmüller character. Since the powers of x intersect every
$\pi $
and the Teichmüller character. Since the powers of x intersect every
![]() $\omega ^j$
-component infinitely many times we can conclude from the preceding reasoning, that
$\omega ^j$
-component infinitely many times we can conclude from the preceding reasoning, that
![]() $W_{int}$
is Zariski-dense. In the general case we consider the finite flat restriction map. Passing to affinoids we first observe that Zariski density inside an affinoid
$W_{int}$
is Zariski-dense. In the general case we consider the finite flat restriction map. Passing to affinoids we first observe that Zariski density inside an affinoid
![]() $\operatorname {Sp}(A)$
in the sense above is equivalent to Zariski density in the scheme
$\operatorname {Sp}(A)$
in the sense above is equivalent to Zariski density in the scheme
![]() $\operatorname {Spec}(A)$
since affinoids are Jacobson. Furthermore, because affinoids are noetherian, we can conclude that the restriction of the map
$\operatorname {Spec}(A)$
since affinoids are Jacobson. Furthermore, because affinoids are noetherian, we can conclude that the restriction of the map
![]() $\rho \colon \mathcal {W}_{an} \to \mathfrak {X}$
to a suitable family of affinoids is finitely presented and flat (in the ring-theoretic sense) and hence (universally) open with respect to the Zariski topology. The claim follows from the preceding density statement because openness implies that the preimage of a dense subset of
$\rho \colon \mathcal {W}_{an} \to \mathfrak {X}$
to a suitable family of affinoids is finitely presented and flat (in the ring-theoretic sense) and hence (universally) open with respect to the Zariski topology. The claim follows from the preceding density statement because openness implies that the preimage of a dense subset of
![]() $\mathfrak {X}$
is dense inside
$\mathfrak {X}$
is dense inside
![]() $\mathcal {W}_{an}.$
Arguing as in the first part, we can show that the image of
$\mathcal {W}_{an}.$
Arguing as in the first part, we can show that the image of
![]() $W_{int}$
inside
$W_{int}$
inside
![]() $\mathfrak {X}$
is dense and hence also
$\mathfrak {X}$
is dense and hence also
![]() $\rho ^{-1}(\rho (W_{int})) = \{ \chi \in \mathcal {W}_{an} \mid \chi _{\mid U}=x^d \}.$
$\rho ^{-1}(\rho (W_{int})) = \{ \chi \in \mathcal {W}_{an} \mid \chi _{\mid U}=x^d \}.$
Remark A.3. Let
![]() $F'/L$
be a finite subextension of K and fix some
$F'/L$
be a finite subextension of K and fix some
![]() $\delta \in \Sigma _{an}(F').$
The map
$\delta \in \Sigma _{an}(F').$
The map
![]() $M \mapsto P(M)$
(for a given property P) corresponds to a unique section of
$M \mapsto P(M)$
(for a given property P) corresponds to a unique section of
![]() $\Gamma (\mathcal {W}_{an}, \mathcal {O}_{\mathcal {W}_{an}})^\times ,$
where we identify
$\Gamma (\mathcal {W}_{an}, \mathcal {O}_{\mathcal {W}_{an}})^\times ,$
where we identify
![]() $\mathcal {W}_{an}$
with the space of analytic twists of
$\mathcal {W}_{an}$
with the space of analytic twists of
![]() $\delta .$
$\delta .$
Proof. We will explain the argument for property (iii). The other properties are treated similarly. We consider the isomorphism
from Theorem 8.6. The validity of property (iii) amounts to the commutativity of the diagram

Since all arrows are isomorphisms, going around the diagram clockwise (starting at
![]() $\mathbf {1}_{D(\Gamma _L,K)}$
) amounts to an automorphism of
$\mathbf {1}_{D(\Gamma _L,K)}$
) amounts to an automorphism of
![]() $D(\Gamma _L,K),$
or in other words, an invertible global section of
$D(\Gamma _L,K),$
or in other words, an invertible global section of
![]() $\mathfrak {X}_{\Gamma _L}.$
The isomorphism
$\mathfrak {X}_{\Gamma _L}.$
The isomorphism
![]() $\Gamma _L \cong o_L^\times $
induces an isomorphism
$\Gamma _L \cong o_L^\times $
induces an isomorphism
![]() $\mathfrak {X}_{\Gamma _L} \cong \mathcal {W}_{an}.$
Hence we get an invertible global section
$\mathfrak {X}_{\Gamma _L} \cong \mathcal {W}_{an}.$
Hence we get an invertible global section
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $\mathcal {W}_{an}.$
This allows us to interpret the validity of property (iii) for every twist
$\mathcal {W}_{an}.$
This allows us to interpret the validity of property (iii) for every twist
![]() $M_K(\delta )$
with
$M_K(\delta )$
with
![]() $\delta \in \mathcal {W}_{an}$
as the section
$\delta \in \mathcal {W}_{an}$
as the section
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $\mathcal {W}_{an}$
constructed above specialising to
$\mathcal {W}_{an}$
constructed above specialising to
![]() $1$
at every such
$1$
at every such
![]() $\delta .$
$\delta .$
Corollary A.4. The set
is Zariski dense.
Proof. Note that the set of de Rham characters contains the set of characters which restrict to a power of x on U and is hence dense in
![]() $\mathcal {W}_{an}.$
As a conclusion the analogously defined set without the genericity condition is dense. For every d there is precisely one
$\mathcal {W}_{an}.$
As a conclusion the analogously defined set without the genericity condition is dense. For every d there is precisely one
![]() $\lambda $
such that
$\lambda $
such that
![]() $\delta _\lambda x^d$
is non-generic. It is not difficult to see that the set S remains dense.
$\delta _\lambda x^d$
is non-generic. It is not difficult to see that the set S remains dense.
To restrict some considerations to
![]() $(\varphi _L,\Gamma _L)$
-modules arising as a base change from a finite extension of L we introduce the following notion.
$(\varphi _L,\Gamma _L)$
-modules arising as a base change from a finite extension of L we introduce the following notion.
Definition A.5. A character
![]() $\rho \colon o_L^\times \to \mathbb {C}_p$
is called classical, if its image is contained in
$\rho \colon o_L^\times \to \mathbb {C}_p$
is called classical, if its image is contained in
![]() $\overline {\mathbb {Q}_p}.$
Analogously a character
$\overline {\mathbb {Q}_p}.$
Analogously a character
![]() $L^\times \to \mathbb {C}_p$
is called classical, if it takes values in
$L^\times \to \mathbb {C}_p$
is called classical, if it takes values in
![]() $\overline {\mathbb {Q}_p}.$
$\overline {\mathbb {Q}_p}.$
Remark A.6.
-
(i) The image of a classical character
 $\rho \colon o_L^\times \to \mathbb {C}_p$
is contained in some finite extension F of
$\rho \colon o_L^\times \to \mathbb {C}_p$
is contained in some finite extension F of
 $\mathbb {Q}_p.$
$\mathbb {Q}_p.$
-
(ii) A character is classical if and only if its restriction to some open subgroup U takes values inside
 $\overline {\mathbb {Q}_p}.$
$\overline {\mathbb {Q}_p}.$
Proof. Since
![]() $o_L^\times $
is topologically finitely generated we can see that the image of some set of topological generators is contained inside
$o_L^\times $
is topologically finitely generated we can see that the image of some set of topological generators is contained inside
![]() $F^\times $
for a suitable finite extension F of
$F^\times $
for a suitable finite extension F of
![]() $\mathbb {Q}_p.$
Moreover, by compactness of
$\mathbb {Q}_p.$
Moreover, by compactness of
![]() $o_L^\times $
, its image is contained inside the maximal compact subgroup
$o_L^\times $
, its image is contained inside the maximal compact subgroup
![]() $o_F^\times \subseteq F^\times $
. Now suppose
$o_F^\times \subseteq F^\times $
. Now suppose
![]() $\rho (U)\subset F$
for some open subgroup
$\rho (U)\subset F$
for some open subgroup
![]() $U\subset o_L^\times .$
Let
$U\subset o_L^\times .$
Let
![]() $\gamma \in o_L^\times ,$
then
$\gamma \in o_L^\times ,$
then
![]() $\gamma ^{[o_L^\times :U]} \in U$
and hence
$\gamma ^{[o_L^\times :U]} \in U$
and hence
![]() $\rho (\gamma )$
is algebraic over
$\rho (\gamma )$
is algebraic over
![]() $F.$
Setting
$F.$
Setting
![]() $F' = F(\rho (\gamma ), \gamma \in \mathfrak {R})$
for a system of representatives
$F' = F(\rho (\gamma ), \gamma \in \mathfrak {R})$
for a system of representatives
![]() $\mathfrak {R} \subset o_L^\times $
of
$\mathfrak {R} \subset o_L^\times $
of
![]() $o_L^\times /U$
we can see that the image of
$o_L^\times /U$
we can see that the image of
![]() $\rho $
is contained in
$\rho $
is contained in
![]() $F'.$
$F'.$
Lemma A.7. Let
![]() $\delta \colon L^\times \to K^\times $
be a de Rham (L-analytic) character, i.e., such that
$\delta \colon L^\times \to K^\times $
be a de Rham (L-analytic) character, i.e., such that
![]() $\mathcal {R}_K(\delta )$
is de Rham in the sense of section 5.4. Then
$\mathcal {R}_K(\delta )$
is de Rham in the sense of section 5.4. Then
![]() $\delta (o_L^\times )\subset \overline {\mathbb {Q}_p}.$
$\delta (o_L^\times )\subset \overline {\mathbb {Q}_p}.$
Proof. Let
![]() $n \gg 0.$
Note that
$n \gg 0.$
Note that
![]() $\mathbf {D}_{\mathrm {dif},n}(\mathcal {R}_K(\delta ))$
embeds
$\mathbf {D}_{\mathrm {dif},n}(\mathcal {R}_K(\delta ))$
embeds
![]() $\Gamma _L$
-equivariantly into
$\Gamma _L$
-equivariantly into
![]() $\prod _{j \in \mathbb {Z}}(L_n\otimes _L K t_{LT}^j(\delta ))$
and the latter is
$\prod _{j \in \mathbb {Z}}(L_n\otimes _L K t_{LT}^j(\delta ))$
and the latter is
![]() $\Gamma _n$
-equivariantly isomorphic to
$\Gamma _n$
-equivariantly isomorphic to
![]() $\prod _{j\in \mathbb {Z}} (\prod _{l=1}^{[L_n:L]} K t_{LT}^j(\delta )).$
The de Rham condition hence forces that
$\prod _{j\in \mathbb {Z}} (\prod _{l=1}^{[L_n:L]} K t_{LT}^j(\delta )).$
The de Rham condition hence forces that
![]() $\delta $
agrees with
$\delta $
agrees with
![]() $\chi _{LT}^j$
for some (unique) j when restricted to
$\chi _{LT}^j$
for some (unique) j when restricted to
![]() $\Gamma _n.$
As a consequence the restriction
$\Gamma _n.$
As a consequence the restriction
![]() $\delta _{\mid _{o_L^\times }}$
is classical.
$\delta _{\mid _{o_L^\times }}$
is classical.
Remark A.8. The proof of the previous Lemma shows that any de Rham L-analytic character
![]() $\delta \colon L^\times \to K^\times $
is of the form
$\delta \colon L^\times \to K^\times $
is of the form
for some
![]() $k\in \mathbb {Z}$
and some locally constant character
$k\in \mathbb {Z}$
and some locally constant character
![]() $\delta _{\mathrm {lc}}:L^\times \to K^\times .$
Vice versa any character of this form is obviously de Rham L-analytic.
$\delta _{\mathrm {lc}}:L^\times \to K^\times .$
Vice versa any character of this form is obviously de Rham L-analytic.
Corollary A.9. Using the notation from A.4 the subset
![]() $S'$
of S consisting of classical points is Zariski dense.
$S'$
of S consisting of classical points is Zariski dense.
Proof. This follows from the following easy observations: The set of characters whose restriction to U is of the form
![]() $x^d$
is classical and the subset of
$x^d$
is classical and the subset of
![]() $\mathbb {G}_m$
defined by
$\mathbb {G}_m$
defined by
![]() $\overline {\mathbb {Q}_p}^\times $
both are Zariski dense.
$\overline {\mathbb {Q}_p}^\times $
both are Zariski dense.
Acknowledgements
We are grateful to Léo Poyeton for discussions about analytic B-pairs and to Kentaro Nakamura for answering generously questions concerning his work. The project has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under TRR 326, Geometry and Arithmetic of Uniformized Structures, project-ID 444845124.
Competing interests
The authors have no competing interests to declare.