Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T08:52:55.808Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DYNAMICAL MORDELL–LANG CONJECTURE FOR ENDOMORPHISMS OF SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC

Part of: Arithmetic and non-Archimedean dynamical systems Arithmetic algebraic geometry

Published online by Cambridge University Press:  24 June 2019

Pietro Corvaja Open the ORCID record for Pietro Corvaja [Opens in a new window] ,
Dragos Ghioca Open the ORCID record for Dragos Ghioca [Opens in a new window] ,
Thomas Scanlon Open the ORCID record for Thomas Scanlon [Opens in a new window]  and
Umberto Zannier Open the ORCID record for Umberto Zannier [Opens in a new window]
Pietro Corvaja
Affiliation:
Dipartimento di Scienze Matematiche, Informatiche e Fisiche, Università di Udine, via delle Scienze, 206, 33100Udine, Italy ([email protected])
Dragos Ghioca
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC V6T 1Z2, Canada ([email protected])
Thomas Scanlon
Affiliation:
University of California, Berkeley, Mathematics Department, Evans Hall, Berkeley, CA94720-3840, USA ([email protected])
Umberto Zannier
Affiliation:
Scuola Normale Superiore, Piazza dei Cavalieri, 7, 56126Pisa, Italy ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 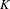$K$ be an algebraically closed field of prime characteristic 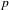$p$, let 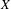$X$ be a semiabelian variety defined over a finite subfield of 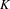$K$, let 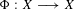$\unicode[STIX]{x1D6F7}:X\longrightarrow X$ be a regular self-map defined over 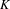$K$, let 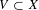$V\subset X$ be a subvariety defined over 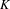$K$, and let 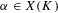$\unicode[STIX]{x1D6FC}\in X(K)$. The dynamical Mordell–Lang conjecture in characteristic 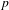$p$ predicts that the set 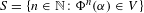$S=\{n\in \mathbb{N}:\unicode[STIX]{x1D6F7}^{n}(\unicode[STIX]{x1D6FC})\in V\}$ is a union of finitely many arithmetic progressions, along with finitely many 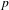$p$-sets, which are sets of the form 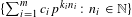$\{\sum _{i=1}^{m}c_{i}p^{k_{i}n_{i}}:n_{i}\in \mathbb{N}\}$ for some 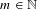$m\in \mathbb{N}$, some rational numbers $c_{i}$ and some non-negative integers 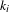$k_{i}$. We prove that this conjecture is equivalent with some difficult diophantine problem in characteristic 0. In the case 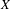$X$ is an algebraic torus, we can prove the conjecture in two cases: either when 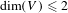$\dim (V)\leqslant 2$, or when no iterate of 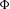$\unicode[STIX]{x1D6F7}$ is a group endomorphism which induces the action of a power of the Frobenius on a positive dimensional algebraic subgroup of 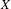$X$. We end by proving that Vojta’s conjecture implies the dynamical Mordell–Lang conjecture for tori with no restriction.

Keywords

dynamical Mordell–Lang problemendomorphisms of semiabelian varieties defined over fields of characteristic p

MSC classification

Primary: 11G10: Abelian varieties of dimension $> 1$
Secondary: 37P55: Arithmetic dynamics on general algebraic varieties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 2 , March 2021 , pp. 669 - 698
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author has been partially supported by a discovery grant from the National Science and Engineering Board of Canada. The third author has been partially supported by grant DMS-1363372 of the United States National Science Foundation and a Simons Foundation Fellowship.

References

Bell, J. P., Ghioca, D. and Tucker, T. J., The Dynamical Mordell–Lang Conjecture, Mathematical Surveys and Monographs, Volume 210, p. xiv+280 pp (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine Geometry, New Mathematical Monographs, Volume 4 (Cambridge University Press, Cambridge, 2006).Google Scholar
Corvaja, P. and Zannier, U., On the Diophantine equation f (a m, y) = b n, Acta Arith. 94(1) (2000), 25–40.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., S-unit points on analytic hypersurfaces, Ann. Sci. Èc. Norm. Super. (4) 38 (2005), 76–92.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., Finiteness of odd perfect powers with four nonzero binary digits, Ann. Inst. Fourier (Grenoble) 63(2) (2013), 715–731.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., Applications of Diophantine Approximation to Integral Points and Transcendence, Cambridge Tracts in Mathematics, Volume 212, p. X + 198 pp (Cambridge University Press, Cambridge, UK, 2018).CrossRefGoogle Scholar
Derksen, H., A Skolem–Mahler–Lech theorem in positive characteristic and finite automata, Invent. Math. 168(1) (2007), 175–224.CrossRefGoogle Scholar
Derksen, H. and Masser, D., Linear equations over multiplicative groups, recurrences, and mixing I, Proc. Lond. Math. Soc. (3) 104(5) (2012), 1045–1083.CrossRefGoogle Scholar
Eisenbud, D., Commutative Algebra: With a View Toward Algebraic Geometry, Graduate Texts in Mathematics, Volume 150 (Springer, New York, 1995).CrossRefGoogle Scholar
Faltings, G., The general case of S. Lang’s conjecture, in Barsotti Symposium in Algebraic Geometry (Albano Terme, 1991), Perspective in Mathematics, Volume 15, pp. 175–182 (Academic Press, San Diego, 1994).CrossRefGoogle Scholar
Ghioca, D., The isotrivial case in the Mordell–Lang theorem, Trans. Amer. Math. Soc. 360(7) (2008), 3839–3856.CrossRefGoogle Scholar
Ghioca, D., The dynamical Mordell–Lang conjecture in positive characteristic, Trans. Amer. Math. Soc. 371(2) (2019), 1151–1167.CrossRefGoogle Scholar
Ghioca, D. and Tucker, T. J., Periodic points, linearizing maps, and the dynamical Mordell–Lang problem, J. Number Theory 129 (2009), 1392–1403.CrossRefGoogle Scholar
Hrushovski, E., The Mordell–Lang conjecture for function fields, J. Amer. Math. Soc. 9(3) (1996), 667–690.CrossRefGoogle Scholar
Laurent, M., Équations diophantiennes exponentielles, Invent. Math. 78(2) (1984), 299–327.CrossRefGoogle Scholar
Lech, C., A note on recurring series, Ark. Mat. 2 (1953), 417–421.CrossRefGoogle Scholar
Mahler, K., On the Taylor coefficients of rational functions, Proc. Cambridge Philos. Soc. 52 (1956), 39–48.CrossRefGoogle Scholar
Masser, D., Mixing and linear equations over groups in positive characteristic, Israel J. Math. 142 (2004), 189–204.CrossRefGoogle Scholar
Milne, J. S., Abelian varieties, version 2.0, 16 March 2008, available at https://www.jmilne.org/math/CourseNotes/av.html.Google Scholar
Moosa, R. and Scanlon, T., F-structures and integral points on semiabelian varieties over finite fields, Amer. J. Math. 126 (2004), 473–522.CrossRefGoogle Scholar
Nelson, K., Two special cases of the dynamical Mordell–Lang conjecture, Master’s thesis, University of British Columbia, March 2017.Google Scholar
Noguchi, J. and Winkelmann, J., Nevanlinna Theory in Several Complex Variables and Diophantine Approximation, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 350, p. xiv+416 pp (Springer, Tokyo, 2014).CrossRefGoogle Scholar
Scanlon, T. and Yasufuku, Y., Exponential-polynomial equations and dynamical return sets, Int. Math. Res. Not. IMRN 2014 (2014), 4357–4367.CrossRefGoogle Scholar
Schmidt, W., Linear recurrence sequences, in Diophantine Approximation (Cetraro, Italy, 2000), Lecture Notes in Mathematics, Volume 1819, pp. 171–247 (Springer, Berlin–Heidelberg, 2003).CrossRefGoogle Scholar
Skolem, T., Ein Verfahren zur Behandlung gewisser exponentialer Gleichungen und diophantischer Gleichungen, C. R. Congr. Math. Scand. (Stockholm, 1934) 163–188.Google Scholar
Vojta, P., Diophantine Approximations and Value Disstribution Theory, Lecture Notes in Mathematics, Volume 1239 (Springer, Berlin–Heidelberg–New York, 1987).CrossRefGoogle Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties, I, Invent. Math. 126 (1996), 133–181.CrossRefGoogle Scholar
Zannier, U., Lecture notes on Diophantine analysis. With an appendix by Francesco Amoroso, Scuola Normale Superiore di Pisa (Nuova Serie) 8. Edizioni della Normale, Pisa, 2009. xvi+237 pp.Google Scholar