No CrossRef data available.
Article contents
DEFORMATIONS OF THE VERONESE EMBEDDING AND FINSLER 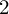 $2$-SPHERES OF CONSTANT CURVATURE
$2$-SPHERES OF CONSTANT CURVATURE
Published online by Cambridge University Press: 20 April 2021
Abstract
We establish a one-to-one correspondence between, on the one hand, Finsler structures on the
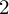 $2$
-sphere with constant curvature
$2$
-sphere with constant curvature
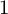 $1$
and all geodesics closed, and on the other hand, Weyl connections on certain spindle orbifolds whose symmetric Ricci curvature is positive definite and whose geodesics are all closed. As an application of our duality result, we show that suitable holomorphic deformations of the Veronese embedding
$1$
and all geodesics closed, and on the other hand, Weyl connections on certain spindle orbifolds whose symmetric Ricci curvature is positive definite and whose geodesics are all closed. As an application of our duality result, we show that suitable holomorphic deformations of the Veronese embedding
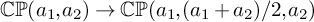 $\mathbb {CP}(a_1,a_2)\rightarrow \mathbb {CP}(a_1,(a_1+a_2)/2,a_2)$
of weighted projective spaces provide examples of Finsler
$\mathbb {CP}(a_1,a_2)\rightarrow \mathbb {CP}(a_1,(a_1+a_2)/2,a_2)$
of weighted projective spaces provide examples of Finsler
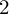 $2$
-spheres of constant curvature whose geodesics are all closed.
$2$
-spheres of constant curvature whose geodesics are all closed.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 2103 - 2134
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press



