Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T20:57:52.808Z Has data issue: false hasContentIssue false
  • English
  • Français

DEFINABLE SETS OF BERKOVICH CURVES

Part of: Arithmetic problems. Diophantine geometry Model theory Topological fields

Published online by Cambridge University Press:  11 October 2019

Pablo Cubides Kovacsics Open the ORCID record for Pablo Cubides Kovacsics [Opens in a new window]  and
Jérôme Poineau Open the ORCID record for Jérôme Poineau [Opens in a new window]
Pablo Cubides Kovacsics
Affiliation:
TU Dresden, Fachrichtung Mathematik, Institut für Algebra, 01062 Dresden, Zellescher Weg 12–14, Willersbau Zi. C 114, Germany ([email protected])
Jérôme Poineau
Affiliation:
Université de Caen, Laboratoire de mathématiques Nicolas Oresme, CNRS UMR 6139, 14032Caen cedex, France ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we functorially associate definable sets to 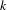$k$-analytic curves, and definable maps to analytic morphisms between them, for a large class of 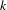$k$-analytic curves. Given a 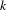$k$-analytic curve 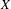$X$, our association allows us to have definable versions of several usual notions of Berkovich analytic geometry such as the branch emanating from a point and the residue curve at a point of type 2. We also characterize the definable subsets of the definable counterpart of 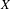$X$ and show that they satisfy a bijective relation with the radial subsets of 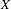$X$. As an application, we recover (and slightly extend) results of Temkin concerning the radiality of the set of points with a given prescribed multiplicity with respect to a morphism of 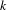$k$-analytic curves. In the case of the analytification of an algebraic curve, our construction can also be seen as an explicit version of Hrushovski and Loeser’s theorem on iso-definability of curves. However, our approach can also be applied to strictly 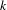$k$-affinoid curves and arbitrary morphisms between them, which are currently not in the scope of their setting.

Keywords

Berkovich spacestable completionalgebraically closed valued fieldradial settopological ramification

MSC classification

Primary: 14G22: Rigid analytic geometry
Secondary: 12J25: Non-Archimedean valued fields 03C98: Applications of model theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 4 , July 2021 , pp. 1275 - 1339
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - ND
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© The Author(s), 2019. Published by Cambridge University Press

Footnotes

The authors were supported by the ERC project TOSSIBERG (grant agreement 637027).

References

Berkovich, V. G., Spectral Theory and Analytic Geometry Over Non-Archimedean Fields, Mathematical Surveys and Monographs, Volume 33 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Berkovich, V. G., Étale cohomology for non-Archimedean analytic spaces, Publ. Math. Inst. Hautes Études Sci. 78 (1993), 5–161. 1994.CrossRefGoogle Scholar
Berkovich, V. G., Smooth p-adic analytic spaces are locally contractible, Invent. Math. 137(1) (1999), 1–84.CrossRefGoogle Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean Analysis, Grundlehren der Mathematischen Wissenschaften, Volume 261 (Springer, Berlin, 1984). A systematic approach to rigid analytic geometry.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXX. Algèbre commutative. Chapitre 5: Entiers. Chapitre 6: Valuations, Actualités Scientifiques et Industrielles, Volume 1308 (Hermann, Paris, 1964).Google Scholar
Cluckers, R. and Lipshitz, L., Fields with analytic structure, J. Eur. Math. Soc. (JEMS) 13(4) (2011), 1147–1223.CrossRefGoogle Scholar
Cohen, A., Temkin, M. and Trushin, D., Morphisms of Berkovich curves and the different function, Adv. Math. 303(Suppl. C) (2016), 800–858.CrossRefGoogle Scholar
Ducros, A., Variation de la dimension relative en géométrie analytique p-adique., Compos. Math. 143(6) (2007), 1511–1532.CrossRefGoogle Scholar
Ducros, A., Les espaces de Berkovich sont excellents, Ann. Inst. Fourier (Grenoble) 59(4) (2009), 1443–1552.CrossRefGoogle Scholar
Ducros, A., Families of Berkovich spaces, Astérisque 400 (2018), vii+262.Google Scholar
Ducros, A., La structure des courbes analytiques. Manuscript available at http://www.math.jussieu.fr/ ducros/trirss.pdf.Google Scholar
Cubides Kovacsics, P., An introduction to C-minimal structures and their cell decomposition theorem, in Valuation Theory and Interaction (ed. Campillo, A., Kuhlmann, F.-V. and Teissier, B.), Congres Reports of the EMS, pp. 167–207 (Eur. Math. Soc., Zürich, 2014).Google Scholar
Foster, T. and Ranganathan, D., Hahn analytification and connectivity of higher rank tropical varieties, Manuscripta Math. 151(3–4) (2016), 353–374.10.1007/s00229-016-0841-3CrossRefGoogle Scholar
Fresnel, J. and van der Put, M., Rigid Analytic Geometry and Its Applications, Progress In Mathematics, Volume 218 (Birkhäuser, Basel, 2004).CrossRefGoogle Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, Volume 52 (Springer, New York–Heidelberg, 1977).CrossRefGoogle Scholar
Haskell, D., Hrushovski, E. and Macpherson, D., Stable Domination and Independence in Algebraically Closed Valued Fields, Lecture Notes in Logic, Volume 30 (Association for Symbolic Logic, Chicago, IL, 2008). Cambridge University Press, Cambridge.Google Scholar
Haskell, D. and Macpherson, D., Cell decompositions of C-minimal structures, Ann. Pure Appl. Logic 66(2) (1994), 113–162.CrossRefGoogle Scholar
Hrushovski, E. and Loeser, F., Non-Archimedean Tame Topology and Stably Dominated Types, Annals of Mathematics Studies, Volume 192 (Princeton University Press, Princeton, NJ, 2016).CrossRefGoogle Scholar
Johnson, W., Fun with field, PhD thesis, University of California, Berkeley (2016).Google Scholar
Lipshitz, L., Rigid subanalytic sets, Amer. J. Math. 115(1) (1993), 77–108.CrossRefGoogle Scholar
Lipshitz, L. and Robinson, Z., One-dimensional fibers of rigid subanalytic sets, J. Symbolic Logic 63(1) (1998), 83–88.CrossRefGoogle Scholar
Pillay, A., Model theory of algebraically closed fields, in Model Theory and Algebraic Geometry, Lecture Notes in Mathematics, Volume 1696, pp. 61–84 (Springer, Berlin, 1998).CrossRefGoogle Scholar
Poineau, J., Les espaces de Berkovich sont angéliques, Bull. Soc. Math. France 141(2) (2013), 267–297.10.24033/bsmf.2648CrossRefGoogle Scholar
Poineau, J. and Bojković, V., Pushforwards of p-adic differential equations, Amer. J. Math., to appear, arXiv:1703.04188 [math.NT].Google Scholar
Poineau, J. and Pulita, A., The convergence Newton polygon of a p-adic differential equation II: Continuity and finiteness on Berkovich curves, Acta Math. 214(2) (2015), 357–393.CrossRefGoogle Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, Volume 44 (Association for Symbolic Logic, Chicago, IL, 2015). Cambridge Scientific Publishers, Cambridge.10.1017/CBO9781107415133CrossRefGoogle Scholar
Temkin, M., Topological transcendence degree, Israel J. Math., to appear, arXiv:1610.09162 [math.AG].Google Scholar
Temkin, M., Metric uniformization of morphisms of Berkovich curves, Adv. Math. 317(Supplement C) (2017), 438–472.CrossRefGoogle Scholar
Welliaveetil, J., Radiality of definable sets, arXiv:1801.00550 [math.AG].Google Scholar