Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T16:33:23.192Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclic stabilizers and infinitely many hyperbolic orbits for pseudogroups on 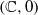$( \mathbb{C} , 0)$

Part of: Complex dynamical systems Differential equations in the complex domain Smooth dynamical systems: general theory

Published online by Cambridge University Press:  06 August 2013

Julio C. Rebelo  and
Helena Reis
Julio C. Rebelo
Affiliation:
Institut de Mathématiques de Toulouse, 118 Route de Narbonne, F-31062 Toulouse, France ([email protected])
Helena Reis
Affiliation:
Centro de Matemática da Universidade do Porto, Faculdade de Economia da Universidade do Porto, Portugal ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a pseudogroup on 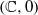$( \mathbb{C} , 0)$ generated by two local diffeomorphisms having analytic conjugacy classes a priori fixed in 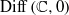$\mathrm{Diff} \hspace{0.167em} ( \mathbb{C} , 0)$. We show that a generic pseudogroup as above is such that every point has a (possibly trivial) cyclic stabilizer. It also follows that these generic groups possess infinitely many hyperbolic orbits. This result possesses several applications to the topology of leaves of foliations, and we shall explicitly describe the case of nilpotent foliations associated to Arnold’s singularities of type 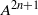${A}^{2n+ 1} $.

Keywords

pseudogroups on (ℂ,0)fixed pointscyclic stabilizers

MSC classification

Secondary: 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations 37F75: Holomorphic foliations and vector fields 34M35: Singularities, monodromy, local behavior of solutions, normal forms
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 2 , April 2014 , pp. 413 - 446
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belliart, M., Liousse, I. and Loray, F., Sur l’existence de points fixes attractifs pour les sous-groupes de $\mathrm{Aut} ( \mathbb{C} , 0)$ , C. R. Acad. Sci. Paris 324 (Sér. I) (1997), 443–446.Google Scholar
Belliart, M., Liousse, I. and Loray, F., The generic differential equation $dw/ dz= {P}_{n} (w, z)/ {Q}_{n} (w, z)$ on $ \mathbb{C} P(2)$ carries no interesting transverse structure, Ergod. Th. & Dynam. Sys. 21 (2001), 1599–1607.Google Scholar
Carleson, L. and Gamelin, T., Complex dynamics. (Springer-Verlag, New York, 1993).Google Scholar
Cerveau, D. and Loray, F., Un théorème de Frobenius singulier via l’arithmétique élémentaire, J. Number Theory 68 (2) (1998), 217–228.Google Scholar
Gomez-Mont, X. and Wirtz, B., On fixed points of conformal pseudogroups, Bull. Braz. Math. Soc. (N, S) 26 (2) (1995), 201–209.Google Scholar
Il’yashenko, Y., Topology of phase portraits of analytic differential equations on a complex projective plane, Tr. Semin. im. I. G. Petrovskogo. 4 (1978), 83–136.Google Scholar
Il’yashenko, Y., Global and local aspects of the theory of complex differential equations, in Proc. Int. Cong. Math. Helsinki, Acad. Scient. Fenn., Volume 2, pp. 821–826 1978).Google Scholar
Katok, A. and Hasselblatt, B., Introduction to the modern theory of dynamical systems, Encyclopedia of Mathematics and its Applications, Volume 54 (Cambridge University Press, 1997).Google Scholar
Le Floch, L., Rigidité générique des feuilletages, Ann. Sc. Éc. Norm. Supér. (4) 31 (6) (1998), 765–785.Google Scholar
Loray, F., Pseudo-groupe d’une singularité de feuilletage holomorphe en dimension deux (available from hal.archives-ouvertes.fr/hal-00016434) (2005).Google Scholar
Marin, D. and Mattei, J.-F., Incompressibilité des feuilles de germes de feuilletages holomorphes singuliers, Ann. Sc. Éc. Norm. Supér. (4) 41 (2008), 855–903.Google Scholar
Mattei, J.-F., Rebelo, J. C. and Reis, H., Generic pseudogroups on $( \mathbb{C} , 0)$ and the topology of leaves, Compositio Math., in press, published online (2013), doi: 10.1112/S0010437X13007161.Google Scholar
Mattei, J.-F. and Salem, E., Modules formels locaux de feuilletages holomorphes, (available from arXiv:math/0402256v1), (2004), 89 pages.Google Scholar
Nakai, I., Separatrices for non solvable dynamics on $( \mathbb{C} , 0)$ , Ann. Inst. Fourier 44 (1994), 569–599.Google Scholar
Shcherbakov, A., On the density of an orbit of a pseudogroup of conformal mappings and a generalization of the Hudai-Verenov theorem, Vestnik Moskov. Univ. Ser. I. Mat. 31 (4) (1982), 10–15.Google Scholar
Shcherbakov, A., Rosales-González, E. and Ortiz-Bobadilla, L., Countable set of limit cycles for the equation $dw/ dz= {P}_{n} (z, w)/ {Q}_{n} (z, w)$ , J. Dyn. Control Syst. 4 (4) (1998), 539–581.CrossRefGoogle Scholar
Takens, F., A nonstabilizable jet of a singularity of a vector field: the analytic case, in Algebraic and differential topology – global differential geometry, Teubner-Text Math., Volume 70, pp. 288–305 (Teubner, Leipzig, 1984).Google Scholar
Yoccoz, J.-C., Centralisateurs et conjugaison différentiable des difféomorphismes du cercle. Petits diviseurs en dimension 1, Astérisque 231 (1995), 89–242.Google Scholar