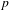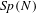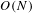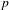Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Xu, Bin
2021.
Nonarchimedean components of non-endoscopic automorphic representations for quasisplit Sp(N) and O(N).
Mathematische Zeitschrift,
Vol. 297,
Issue. 1-2,
p.
885.
Atobe, Hiraku
2022.
Construction of local A-packets.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 790,
p.
1.
Atobe, Hiraku
2022.
On an algorithm to compute derivatives.
manuscripta mathematica,
Vol. 167,
Issue. 3-4,
p.
721.
Atobe, Hiraku
2023.
The set of local 𝐴-packets containing a given representation.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Xu, Bin
2024.
Arthur Packets for Quasisplit GSp(2n) and GO(2n) Over a p-Adic Field.
International Mathematics Research Notices,
Vol. 2024,
Issue. 13,
p.
10349.
Hazeltine, Alexander
Liu, Baiying
Lo, Chi-Heng
and
Zhang, Qing
2025.
The closure ordering conjecture on local Arthur packets of classical groups.
Journal für die reine und angewandte Mathematik (Crelles Journal),