Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-08T19:27:58.941Z Has data issue: false hasContentIssue false
  • English
  • Français

A CLASSIFICATION OF LAGRANGIAN PLANES IN HOLOMORPHIC SYMPLECTIC VARIETIES

Part of: Birational geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  09 September 2015

Benjamin Bakker
Benjamin Bakker*
Affiliation:
Institut für Mathematik, Humboldt-Universität zu Berlin, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Classically, an indecomposable class 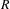$R$ in the cone of effective curves on a K3 surface 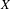$X$ is representable by a smooth rational curve if and only if 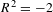$R^{2}=-2$. We prove a higher-dimensional generalization conjectured by Hassett and Tschinkel: for a holomorphic symplectic variety 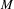$M$ deformation equivalent to a Hilbert scheme of $n$ points on a K3 surface, an extremal curve class 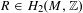$R\in H_{2}(M,\mathbb{Z})$ in the Mori cone is the line in a Lagrangian $n$-plane 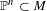$\mathbb{P}^{n}\subset M$ if and only if certain intersection-theoretic criteria are met. In particular, any such class satisfies 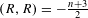$(R,R)=-\frac{n+3}{2}$, and the primitive such classes are all contained in a single monodromy orbit.

Keywords

holomorphic symplectic varietyextremal rayLagrangian subvariety

MSC classification

Primary: 14J40: $n$-folds ($n>4$)
Secondary: 14E30: Minimal model program (Mori theory, extremal rays) 14J28: $K3$ surfaces and Enriques surfaces
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 4 , September 2017 , pp. 859 - 877
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arcara, D. and Bertram, A., Bridgeland-stable moduli spaces for K-trivial surfaces, J. Eur. Math. Soc. (JEMS) 15(1) (2013), 1–38. With an appendix by Max Lieblich.Google Scholar
Bartocci, C., Bruzzo, U. and Hernández Ruipérez, D., Fourier–Mukai and Nahm Transforms in Geometry and Mathematical Physics, Progress in Mathematics, vol. 276 (Birkhäuser Boston Inc., Boston, MA, 2009).CrossRefGoogle Scholar
Bayer, A., Hassett, B. and Tschinkel, Y., Mori cones of holomorphic symplectic varieties of K3 type, 2013, arXiv:1307.2291.Google Scholar
Bakker, B. and Jorza, A., Lagrangian 4-planes in holomorphic symplectic varieties of K3[4] -type, Cent. Eur. J. Math. 12(7) (2014), 952–975.Google Scholar
Bayer, A. and Macrì, E., MMP for moduli of sheaves on K3s via wall-crossing: nef and movable cones, Lagrangian fibrations, Invent. Math. 198(3) (2014), 505–590.CrossRefGoogle Scholar
Bayer, A. and Macrì, E., Projectivity and birational geometry of Bridgeland moduli spaces, J. Amer. Math. Soc. 27(3) (2014), 707–752.CrossRefGoogle Scholar
Bridgeland, T., Stability conditions on triangulated categories, Ann. of Math. (2) 166(2) (2007), 317–345.CrossRefGoogle Scholar
Bridgeland, T., Stability conditions on K3 surfaces, Duke Math. J. 141(2) (2008), 241–291.CrossRefGoogle Scholar
Cho, K., Miyaoka, Y. and Shepherd-Barron, N. I., Characterizations of projective space and applications to complex symplectic manifolds, in Higher Dimensional Birational Geometry (Kyoto, 1997), Adv. Stud. Pure Math., Volume 35, pp. 1–88 (Math. Soc. Japan, Tokyo, 2002).Google Scholar
Eichler, M., Quadratische Formen und orthogonale Gruppen (Springer, Berlin, 1974). Zweite Auflage, Die Grundlehren der mathematischen Wissenschaften, Band 63.CrossRefGoogle Scholar
Gritsenko, V., Hulek, K. and Sankaran, G. K., Moduli spaces of irreducible symplectic manifolds, Compos. Math. 146(2) (2010), 404–434.CrossRefGoogle Scholar
Harvey, D., Hassett, B. and Tschinkel, Y., Characterizing projective spaces on deformations of Hilbert schemes of K3 surfaces, Comm. Pure Appl. Math. 65(2) (2012), 264–286.CrossRefGoogle Scholar
Huybrechts, D. and Stellari, P., Equivalences of twisted K3 surfaces, Math. Ann. 332(4) (2005), 901–936.CrossRefGoogle Scholar
Hassett, B. and Tschinkel, Y., Rational curves on holomorphic symplectic fourfolds, Geom. Funct. Anal. 11(6) (2001), 1201–1228.Google Scholar
Huybrechts, D. and Thomas, R. P., ℙ-objects and autoequivalences of derived categories, Math. Res. Lett. 13(1) (2006), 87–98.CrossRefGoogle Scholar
Hassett, B. and Tschinkel, Y., Moving and ample cones of holomorphic symplectic fourfolds, Geom. Funct. Anal. 19(4) (2009), 1065–1080.CrossRefGoogle Scholar
Hassett, B. and Tschinkel, Y., Intersection numbers of extremal rays on holomorphic symplectic varieties, Asian J. Math. 14(3) (2010), 303–322.CrossRefGoogle Scholar
Hassett, B. and Tschinkel, Y., Hodge theory and Lagrangian planes on generalized Kummer fourfolds, Mosc. Math. J. 13(1) (2013), 33–56, 189.CrossRefGoogle Scholar
Inaba, M., Toward a definition of moduli of complexes of coherent sheaves on a projective scheme, Kyoto J. Math. 42(2) (2002), 317–329.CrossRefGoogle Scholar
Lieblich, M., Moduli of complexes on a proper morphism, J. Algebraic Geom. 15(1) (2006), 175–206.CrossRefGoogle Scholar
Markman, E., Brill–Noether duality for moduli spaces of sheaves on K3 surfaces, J. Algebraic Geom. 10(4) (2001), 623–694.Google Scholar
Markman, E., A survey of Torelli and monodromy results for holomorphic-symplectic varieties, in Complex and Differential Geometry, Springer Proceedings in Mathematics, Volume 8, pp. 257–322 (Springer, Heidelberg, 2011).CrossRefGoogle Scholar
Markman, E., Lagrangian fibrations of holomorphic-symplectic varieties of K3[n] -type, in Algebraic and Complex Geometry, Springer Proc. Math. Stat., Volume 71, pp. 241–283 (Springer, Cham, 2014).CrossRefGoogle Scholar
Mongardi, G., A note on the Kähler and Mori cones of hyperkähler manifolds, 2013, arXiv:1307.0393.Google Scholar
Minamide, H., Yanagida, S. and Yoshioka, K., Some moduli spaces of Bridgeland’s stability conditions, Int. Math. Res. Not. IMRN 19 (2014), 5264–5327.CrossRefGoogle Scholar
Namikawa, Y., Deformation theory of singular symplectic n-folds, Math. Ann. 319(3) (2001), 597–623.CrossRefGoogle Scholar
Ran, Z., Hodge theory and deformations of maps, Compos. Math. 97(3) (1995), 309–328.Google Scholar
Toda, Y., Semistable objects in derived categories of K3 surfaces, in Higher Dimensional Algebraic Varieties and Vector Bundles, RIMS Kôkyûroku Bessatsu, Volume B9, pp. 175–188 (Res. Inst. Math. Sci. (RIMS), Kyoto, 2008).Google Scholar
Verbitsky, M., Mapping class group and a global Torelli theorem for hyperkähler manifolds, Duke Math. J. 162(15) (2013), 2929–2986. Appendix A by Eyal Markman.CrossRefGoogle Scholar
Voisin, C., Sur la stabilité des sous-variétés Lagrangiennes des variétés symplectiques holomorphes, Complex projective geometry 179 (1992), 294.CrossRefGoogle Scholar
Yoshioka, K., Moduli spaces of stable sheaves on abelian surfaces, Math. Ann. 321(4) (2001), 817–884.CrossRefGoogle Scholar
Yoshioka, K., Bridgeland’s stability and the positive cone of the moduli spaces of stable objects on an abelian surface, 2012, arXiv:1206.4838.Google Scholar