Article contents
CHARACTERIZING O-MINIMAL GROUPS IN TAME EXPANSIONS OF O-MINIMAL STRUCTURES
Published online by Cambridge University Press: 16 July 2019
Abstract
We establish the first global results for groups definable in tame expansions of o-minimal structures. Let 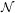 ${\mathcal{N}}$
be an expansion of an o-minimal structure
${\mathcal{N}}$
be an expansion of an o-minimal structure 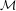 ${\mathcal{M}}$
that admits a good dimension theory. The setting includes dense pairs of o-minimal structures, expansions of
${\mathcal{M}}$
that admits a good dimension theory. The setting includes dense pairs of o-minimal structures, expansions of 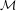 ${\mathcal{M}}$
by a Mann group, or by a subgroup of an elliptic curve, or a dense independent set. We prove: (1) a Weil’s group chunk theorem that guarantees a definable group with an o-minimal group chunk is o-minimal, (2) a full characterization of those definable groups that are o-minimal as those groups that have maximal dimension; namely, their dimension equals the dimension of their topological closure, (3) as an application, if
${\mathcal{M}}$
by a Mann group, or by a subgroup of an elliptic curve, or a dense independent set. We prove: (1) a Weil’s group chunk theorem that guarantees a definable group with an o-minimal group chunk is o-minimal, (2) a full characterization of those definable groups that are o-minimal as those groups that have maximal dimension; namely, their dimension equals the dimension of their topological closure, (3) as an application, if 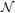 ${\mathcal{N}}$
expands
${\mathcal{N}}$
expands 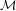 ${\mathcal{M}}$
by a dense independent set, then every definable group is o-minimal.
${\mathcal{M}}$
by a dense independent set, then every definable group is o-minimal.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 2 , March 2021 , pp. 699 - 724
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2019. Published by Cambridge University Press
Footnotes
The research was supported by an Independent Research Grant from the German Research Foundation (DFG) and a Zukunftskolleg Research Fellowship.
References
- 2
- Cited by



