Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T22:43:13.892Z Has data issue: false hasContentIssue false
  • English
  • Français

CENTRAL LIMIT THEOREM FOR THE MODULUS OF CONTINUITY OF AVERAGES OF OBSERVABLES ON TRANSVERSAL FAMILIES OF PIECEWISE EXPANDING UNIMODAL MAPS

Part of: Ergodic theory Low-dimensional dynamical systems Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  13 July 2016

Amanda de Lima  and
Daniel Smania
Amanda de Lima
Affiliation:
Departamento de Matemática, ICMC-USP, Caixa Postal 668, São Carlos-SP, CEP 13560-970 São Carlos-SP, Brazil ([email protected]; [email protected]); URL: www.icmc.usp.br/∼smania/
Daniel Smania
Affiliation:
Departamento de Matemática, ICMC-USP, Caixa Postal 668, São Carlos-SP, CEP 13560-970 São Carlos-SP, Brazil ([email protected]; [email protected]); URL: www.icmc.usp.br/∼smania/
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a 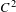$C^{2}$ family of mixing 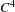$C^{4}$ piecewise expanding unimodal maps 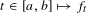$t\in [a,b]\mapsto f_{t}$, with a critical point $c$, that is transversal to the topological classes of such maps. Given a Lipchitz observable 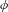$\unicode[STIX]{x1D719}$ consider the function

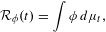$$\begin{eqnarray}{\mathcal{R}}_{\unicode[STIX]{x1D719}}(t)=\int \unicode[STIX]{x1D719}\,d\unicode[STIX]{x1D707}_{t},\end{eqnarray}$$
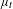where $\unicode[STIX]{x1D707}_{t}$ is the unique absolutely continuous invariant probability of 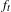$f_{t}$. Suppose that 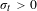$\unicode[STIX]{x1D70E}_{t}>0$ for every 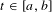$t\in [a,b]$, where
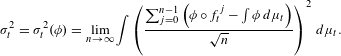$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{t}^{2}=\unicode[STIX]{x1D70E}_{t}^{2}(\unicode[STIX]{x1D719})=\lim _{n\rightarrow \infty }\int \left(\frac{\mathop{\sum }_{j=0}^{n-1}\left(\unicode[STIX]{x1D719}\circ f_{t}^{j}-\int \unicode[STIX]{x1D719}\,d\unicode[STIX]{x1D707}_{t}\right)}{\sqrt{n}}\right)^{2}\,d\unicode[STIX]{x1D707}_{t}.\end{eqnarray}$$

We show that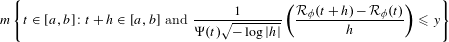

$$\begin{eqnarray}m\left\{t\in [a,b]:t+h\in [a,b]\text{ and }\frac{1}{\unicode[STIX]{x1D6F9}(t)\sqrt{-\log |h|}}\left(\frac{{\mathcal{R}}_{\unicode[STIX]{x1D719}}(t+h)-{\mathcal{R}}_{\unicode[STIX]{x1D719}}(t)}{h}\right)\leqslant y\right\}\end{eqnarray}$$
converges to
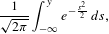$$\begin{eqnarray}\frac{1}{\sqrt{2\unicode[STIX]{x1D70B}}}\int _{-\infty }^{y}e^{-\frac{s^{2}}{2}}\,ds,\end{eqnarray}$$
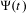 where $\unicode[STIX]{x1D6F9}(t)$ is a dynamically defined function and 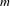$m$ is the Lebesgue measure on 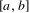$[a,b]$, normalized in such way that 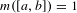$m([a,b])=1$. As a consequence, we show that 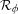${\mathcal{R}}_{\unicode[STIX]{x1D719}}$ is not a Lipchitz function on any subset of 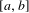$[a,b]$ with positive Lebesgue measure.

Keywords

linear responsedynamical systemsunimodal mapsexpanding mapsergodic theoryCentral Limit Theorem

MSC classification

Primary: 37C30: Zeta functions, (Ruelle-Frobenius) transfer operators, and other functional analytic techniques in dynamical systems 37C40: Smooth ergodic theory, invariant measures 37D50: Hyperbolic systems with singularities (billiards, etc.) 37E05: Maps of the interval (piecewise continuous, continuous, smooth) 37A05: Measure-preserving transformations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 3 , June 2018 , pp. 673 - 733
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baladi, V., On the susceptibility function of piecewise expanding interval maps, Comm. Math. Phys. 275(3) (2007), 839–859.CrossRefGoogle Scholar
Baladi, V. and Smania, D., Linear response formula for piecewise expanding unimodal maps, Nonlinearity 21(4) (2008), 677–711.Google Scholar
Baladi, V. and Smania, D., Smooth deformations of piecewise expanding unimodal maps, Discrete Contin. Dyn. Syst. 23(3) (2009), 685–703.CrossRefGoogle Scholar
Baladi, V. and Smania, D., Alternative proofs of linear response for piecewise expanding unimodal maps, Ergod. Th. & Dynam. Sys. 30(1) (2010), 1–20.Google Scholar
Baladi, V. and Smania, D., Corrigendum: linear response formula for piecewise expanding unimodal maps, Nonlinearity 25(7) (2012), 2203–2205.CrossRefGoogle Scholar
Billingsley, P., Convergence of Probability Measures, second edition, Wiley Series in Probability and Statistics: Probability and Statistics (John Wiley & Sons, Inc., New York, 1999). A Wiley–Interscience Publication.Google Scholar
Contreras, F., Regularity of absolutely continuous invariant measures for piecewise expanding unimodal maps, PhD’s thesis. University of Maryland (2015).CrossRefGoogle Scholar
Karatzas, I. and Shreve, S. E., Brownian Motion and Stochastic Calculus, second edition, Graduate Texts in Mathematics, Volume 113 (Springer-Verlag, New York, 1991).Google Scholar
Keller, G., Stochastic stability in some chaotic dynamical systems, Monatsh. Math. 94(4) (1982), 313–333.CrossRefGoogle Scholar
Keller, G., Generalized bounded variation and applications to piecewise monotonic transformations, Z. Wahrsch. Verw. Gebiete 69(3) (1985), 461–478.Google Scholar
Keller, G., Howard, P. J. and Klages, R., Continuity properties of transport coefficients in simple maps, Nonlinearity 21(8) (2008), 1719–1743.CrossRefGoogle Scholar
Lasota, A. and Yorke, J. A., On the existence of invariant measures for piecewise monotonic transformations, Trans. Amer. Math. Soc. 186 (1974), 481–488.Google Scholar
Leplaideur, R. and Saussol, B., Central limit theorem for dimension of Gibbs measures in hyperbolic dynamics, Stoch. Dyn. 12(2) (2012), 1150019, 24.Google Scholar
Mazzolena, M., Dinamiche espansive unidimensionali: dipendenza della misura invariante da un parametro, Master’s thesis Roma 2, Tor Vergata (2007).Google Scholar
Philipp, W. and Stout, W., Almost sure invariance principles for partial sums of weakly dependent random variables, Mem. Amer. Math. Soc. 2(2) (1975), no. 161, iv+140 pp.Google Scholar
Ruelle, D., Differentiation of SRB states, Comm. Math. Phys. 187(1) (1997), 227–241.Google Scholar
Ruelle, D., Nonequilibrium statistical mechanics near equilibrium: computing higher-order terms, Nonlinearity 11(1) (1998), 5–18.Google Scholar
Schnellmann, D., Typical points for one-parameter families of piecewise expanding maps of the interval, Discrete Contin. Dyn. Syst. 31(3) (2011), 877–911.Google Scholar
Schnellmann, D., Law of iterated logarithm and invariance principle for one-parameter families of interval maps, Probab. Theory Related Fields 162(1–2) (2015), 365–409.Google Scholar
Tsujii, M., A simple proof for monotonicity of entropy in the quadratic family, Ergod. Th. & Dynam. Sys. 20(3) (2000), 925–933.Google Scholar
Viana, M., Sthochastic Dynamics of Deterministic Systems, Lecture Notes XXI Colóquio Brasileiro de Matemática (IMPA, Rio de Janeiro, 1997).Google Scholar