Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T08:20:43.401Z Has data issue: false hasContentIssue false
  • English
  • Français

Bruhat–Tits theory from Berkovich's point of view. II Satake compactifications of buildings

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  13 December 2011

Bertrand Rémy ,
Amaury Thuillier  and
Annette Werner
Bertrand Rémy
Affiliation:
Université de Lyon, Université Lyon 1, CNRS—UMR 5208, Institut Camille Jordan, 43 boulevard du 11 novembre 1918, F-69622 Villeurbanne cedex, France ([email protected]; [email protected])
Amaury Thuillier
Affiliation:
Université de Lyon, Université Lyon 1, CNRS—UMR 5208, Institut Camille Jordan, 43 boulevard du 11 novembre 1918, F-69622 Villeurbanne cedex, France ([email protected]; [email protected])
Annette Werner
Affiliation:
Institut für Mathematik, Goethe-Universität Frankfurt, Robert-Mayer-Strasse 6–8, D-60325 Frankfurt a.M., Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In the paper ‘Bruhat–Tits theory from Berkovich's point of view. I. Realizations and compactifications of buildings’, we investigated various realizations of the Bruhat–Tits building 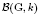of a connected and reductive linear algebraic group G over a non-Archimedean field k in the framework of Berkovich's non-Archimedean analytic geometry. We studied in detail the compactifications of the building which naturally arise from this point of view. In the present paper, we give a representation theoretic flavour to these compactifications, following Satake's original constructions for Riemannian symmetric spaces.

We first prove that Berkovich compactifications of a building coincide with the compactifications, previously introduced by the third named author and obtained by a gluing procedure. Then we show how to recover them from an absolutely irreducible linear representation of G by embedding 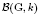in the building of the general linear group of the representation space, compactified in a suitable way. Existence of such an embedding is a special case of Landvogt's general results on functoriality of buildings, but we also give another natural construction of an equivariant embedding, which relies decisively on Berkovich geometry.

Keywords

algebraic grouplocal fieldBerkovich geometryBruhat–Tits buildingcompactification

MSC classification

Secondary: 20E42: Groups with a $BN$-pair; buildings
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 11 , Issue 2 , April 2012 , pp. 421 - 465
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Berkovich, V. G., Spectral theory and analytic geometry over non-archimedean fields, Mathematical Surveys and Monographs, Volume 33 (American Mathematical Society, Providence, RI, 1990).Google Scholar
2.Berkovich, V. G., The automorphism group of the Drinfeld half-plane, C. R. Acad. Sci. Paris 321 (1995), 1127–1132.Google Scholar
3.Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, Volume 126 (Springer, 1991).CrossRefGoogle Scholar
4.Borel, A. and Tits, J., Groupes réductifs, Publ. Math. IHES 27 (1965), 55–150.CrossRefGoogle Scholar
5.Bosch, S., Güntzer, U. and Remmert, R., Non-archimedean analysis, Grundlehren der Mathematischen Wissenschaften, Volume 261 (Springer, 1984).CrossRefGoogle Scholar
6.Bruhat, F. and Tits, J., Schémas en groupes et immeubles des groupes classiques sur un corps local, Bull. Soc. Math. France 112 (1984), 259–301.CrossRefGoogle Scholar
7.Chevalley, C., Classification des groupes algébriques semi-simples, CollectedWorks, Volume 3 (Springer, 2005).Google Scholar
8.Demazure, M. and Grothendieck, A. (eds), Schémas en groupes. Séminaire de géométrie algébrique du Bois Marie 1962/64 (SGA 3), Lecture Notes in Mathematics, Volume 151–153 (Springer, 1970).Google Scholar
9.Goldman, O. and Iwahori, N., The space of p-adic norms, Acta Math. 109 (1963), 137–177.CrossRefGoogle Scholar
10.Guivarc'h, Y. and Rémy, B., Group theoretic compactification of Bruhat–Tits buildings, Annales Scient. Éc. Norm. Sup. 39 (2006), 871–920.CrossRefGoogle Scholar
11.Landvogt, E., Some functorial properties of the Bruhat–Tits building, J. Reine Angew. Math. 518 (2000), 213–241.Google Scholar
12.Rémy, B., Thuillier, A. and Werner, A., Bruhat–Tits theory from Berkovich's point of view, I, Realizations and compactifications of buildings, Annales Scient. Éc. Norm. Sup. 43 (2010), 461–554.CrossRefGoogle Scholar
13.Satake, I., On representations and compactifications of symmetric Riemannian spaces, Annals Math. 71 (1960), 77–110.CrossRefGoogle Scholar
14.Werner, A., Compactification of the Bruhat–Tits building of PGL by lattices of smaller rank, Documenta Math. 6 (2001), 315–341.CrossRefGoogle Scholar
15.Werner, A., Compactification of the Bruhat–Tits building of PGL by seminorms, Math. Z. 248 (2004), 511–526.CrossRefGoogle Scholar
16.Werner, A., Compactifications of Bruhat–Tits buildings associated to linear representations, Proc. Lond. Math. Soc. 95 (2007), 497–518.CrossRefGoogle Scholar