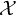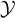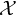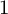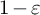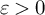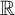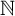1 Introduction
All Banach spaces considered in this paper are infinite dimensional and over the reals. For unexplained terminology, see Section 2. If
![]() $\mathcal {X}$
is a Banach space,
$\mathcal {X}$
is a Banach space,
![]() $\mathcal {Y}\subseteq \mathcal {X}$
and
$\mathcal {Y}\subseteq \mathcal {X}$
and
![]() $r>0$
, we say that
$r>0$
, we say that
![]() $\mathcal {Y}$
is
$\mathcal {Y}$
is
-
•
 $(r+)$
-separated if
$(r+)$
-separated if
 $\|y-y'\|>r$
for any two distinct
$\|y-y'\|>r$
for any two distinct
 $y, y'\in \mathcal {Y}$
,
$y, y'\in \mathcal {Y}$
, -
• r-separated if
 $\|y-y'\|\geq r$
for any two distinct
$\|y-y'\|\geq r$
for any two distinct
 $y, y'\in \mathcal {Y}$
,
$y, y'\in \mathcal {Y}$
, -
• r-concentrated if
 $\|y-y'\|\leq r$
for any two distinct
$\|y-y'\|\leq r$
for any two distinct
 $y, y'\in \mathcal {Y}$
,
$y, y'\in \mathcal {Y}$
, -
• r-equilateral if
 $\|y-y'\|=r$
for any two distinct
$\|y-y'\|=r$
for any two distinct
 $y, y'\in \mathcal {Y}$
,
$y, y'\in \mathcal {Y}$
, -
• equilateral if it is r-equilateral for some
 $r>0$
.
$r>0$
.
The classical Riesz lemma of 1916 (If
![]() $\mathcal {Y}$
is a closed proper subspace of
$\mathcal {Y}$
is a closed proper subspace of
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\varepsilon>0$
, then there is x in the unit sphere of
$\varepsilon>0$
, then there is x in the unit sphere of
![]() $\mathcal {X}$
such that the distance of x from
$\mathcal {X}$
such that the distance of x from
![]() $\mathcal {Y}$
does exceed
$\mathcal {Y}$
does exceed
![]() $1-\varepsilon $
, [Reference Riesz44]) allows one to construct
$1-\varepsilon $
, [Reference Riesz44]) allows one to construct
![]() $(1-\varepsilon )$
-separated sets of the cardinality equal to the density of a Banach space and in its unit sphere. By the compactness of the balls in finite-dimensional spaces it also yields infinite
$(1-\varepsilon )$
-separated sets of the cardinality equal to the density of a Banach space and in its unit sphere. By the compactness of the balls in finite-dimensional spaces it also yields infinite
![]() $1$
-separated sets in any infinite dimensional Banach space. Kottman proved in 1975 [Reference Kottman30] that the unit sphere of every infinite-dimensional Banach space admits an infinite
$1$
-separated sets in any infinite dimensional Banach space. Kottman proved in 1975 [Reference Kottman30] that the unit sphere of every infinite-dimensional Banach space admits an infinite
![]() $(1+)$
-separated subset, which was improved in 1981 by Elton and Odell to
$(1+)$
-separated subset, which was improved in 1981 by Elton and Odell to
![]() $(1+\varepsilon )$
-separated for some
$(1+\varepsilon )$
-separated for some
![]() $\varepsilon>0$
[Reference Elton and Odell9]Footnote
1
who also noted that
$\varepsilon>0$
[Reference Elton and Odell9]Footnote
1
who also noted that
![]() $c_0(\omega _1)$
does not admit an uncountable
$c_0(\omega _1)$
does not admit an uncountable
![]() $(1+\varepsilon )$
-separated set. The Kottman constant of a Banach space (the supremum over
$(1+\varepsilon )$
-separated set. The Kottman constant of a Banach space (the supremum over
![]() $\delta>0$
such that there is an infinite
$\delta>0$
such that there is an infinite
![]() $\delta $
-separated subset of the unit sphere) turned out to be an important tool used for investigating the geometry of the space (e.g., [Reference Castillo, González and Papini3, Reference Kryczka and Prus32, Reference van Neerven40, Reference Maluta and Papini34, Reference Baronti, Casini and Papini1, Reference Papini41]). In fact, it is related to many aspects of Banach spaces such as, for example, packing balls, measures of noncompactness, fixed points, average distances and infinite dimensional convexity (see, e.g., the papers citing [Reference Kottman31] or [Reference Elton and Odell9]).
$\delta $
-separated subset of the unit sphere) turned out to be an important tool used for investigating the geometry of the space (e.g., [Reference Castillo, González and Papini3, Reference Kryczka and Prus32, Reference van Neerven40, Reference Maluta and Papini34, Reference Baronti, Casini and Papini1, Reference Papini41]). In fact, it is related to many aspects of Banach spaces such as, for example, packing balls, measures of noncompactness, fixed points, average distances and infinite dimensional convexity (see, e.g., the papers citing [Reference Kottman31] or [Reference Elton and Odell9]).
It has been clear, at least since the paper [Reference Mercourakis and Vassiliadis38] of Mercourakis and Vassiliadis, that the nature of separation in uncountable subsets of the unit sphere of a nonseparable Banach space could be equally indicative of the global and diverse properties of the space as in the separable case. The question of whether the unit sphere of a nonseparable Banach space must contain an uncountable
![]() $(1+)$
-separated set and if so, of what cardinality compared to the density of the space, has been studied for various classes of Banach spaces, for exampl, in [Reference Cúth, Kurka and Vejnar5, Reference Kania and Kochanek25, Reference Mercourakis and Vassiliadis37, Reference Mercourakis and Vassiliadis38] and recently culminated in the paper [Reference Hájek, Kania and Russo19], where it is highlighted as a central question. Notably, the existence of
$(1+)$
-separated set and if so, of what cardinality compared to the density of the space, has been studied for various classes of Banach spaces, for exampl, in [Reference Cúth, Kurka and Vejnar5, Reference Kania and Kochanek25, Reference Mercourakis and Vassiliadis37, Reference Mercourakis and Vassiliadis38] and recently culminated in the paper [Reference Hájek, Kania and Russo19], where it is highlighted as a central question. Notably, the existence of
![]() $(1+\varepsilon )$
-separated sets of the size equal to the density of the space was proved for superreflexive Banach spaces by Kania and Kochanek in [Reference Kania and Kochanek25] and for
$(1+\varepsilon )$
-separated sets of the size equal to the density of the space was proved for superreflexive Banach spaces by Kania and Kochanek in [Reference Kania and Kochanek25] and for
![]() $C(K)$
spaces, where K is compact Hausdorff and totally disconnected by Mercourakis and Vassiliadis. Moreover Hájek, Kania and Russo proved in [Reference Hájek, Kania and Russo19] that uncountable
$C(K)$
spaces, where K is compact Hausdorff and totally disconnected by Mercourakis and Vassiliadis. Moreover Hájek, Kania and Russo proved in [Reference Hájek, Kania and Russo19] that uncountable
![]() $(1+)$
-separated sets exist in any Banach space of sufficiently large density. However, we provide quite a strong negative answer to the general question:
$(1+)$
-separated sets exist in any Banach space of sufficiently large density. However, we provide quite a strong negative answer to the general question:
Theorem 1. There is a (strictly convex) Banach space of density continuum where every uncountable subset of the unit sphere of regular cardinality
![]() $\kappa $
includes a subset of the same cardinality which is
$\kappa $
includes a subset of the same cardinality which is
![]() $(1-\varepsilon )$
-concentrated for some
$(1-\varepsilon )$
-concentrated for some
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
To prove it, apply Propositions 15 and 10 obtaining the validity of their hypotheses by Lemmas 12 and 7, respectively. The strength of the above propertyFootnote 2 may be appreciated by seeing how easily it yields the next two theorems which provide other natural properties of Banach spaces unknown to occur until now without making some additional consistent but unprovable set-theoretic assumptions.
Recall an observation of Terenzi from [Reference Terenzi48] that, if
![]() $\mathcal {Y}$
is an equilateral set in a Banach space
$\mathcal {Y}$
is an equilateral set in a Banach space
![]() $\mathcal {X}$
, by scaling we may assume that it is a
$\mathcal {X}$
, by scaling we may assume that it is a
![]() $1$
-equilateral set, and then by considering
$1$
-equilateral set, and then by considering
![]() $\{y_0-y: y\in \mathcal {Y}\setminus \{y_0\}\}$
for any
$\{y_0-y: y\in \mathcal {Y}\setminus \{y_0\}\}$
for any
![]() $y_0\in \mathcal {Y}$
we obtain a
$y_0\in \mathcal {Y}$
we obtain a
![]() $1$
-equilateral set consisting of elements of the unit sphere of
$1$
-equilateral set consisting of elements of the unit sphere of
![]() $\mathcal {X}$
. So Theorem 1 yields:
$\mathcal {X}$
. So Theorem 1 yields:
Theorem 2. There is a (strictly convex) Banach space of density continuum which does not admit an uncountable equilateral set.
Banach spaces with this property were previously consistently constructed by the author in [Reference Koszmider27]. These spaces were of the form
![]() $C(K)$
for K compact Hausdorff, while it was also proved in [Reference Koszmider27] that consistently every Banach space of the form
$C(K)$
for K compact Hausdorff, while it was also proved in [Reference Koszmider27] that consistently every Banach space of the form
![]() $C(K)$
admits an uncountable equilateral set.
$C(K)$
admits an uncountable equilateral set.
Different examples of Banach spaces satisfying Theorem 2 which also do not require any additional set-theoretic assumptions are being presented at the same time in a joint paper of the author with H.M. Wark [Reference Koszmider and Wark29]. They are renormings of
![]() $\ell _1([0,1])$
, and moreover they do not admit even any infinite equilateral set (However, all equivalent renormings of
$\ell _1([0,1])$
, and moreover they do not admit even any infinite equilateral set (However, all equivalent renormings of
![]() $\ell _1(\Gamma )$
for
$\ell _1(\Gamma )$
for
![]() $\Gamma $
uncountable admit
$\Gamma $
uncountable admit
![]() $(1+\varepsilon )$
-separated set of size
$(1+\varepsilon )$
-separated set of size
![]() $\Gamma $
by Remark 3.16 of [Reference Hájek, Kania and Russo19]). The above theorem solves Problem 293 of [Reference Guirao, Montesinos and Zizler16].
$\Gamma $
by Remark 3.16 of [Reference Hájek, Kania and Russo19]). The above theorem solves Problem 293 of [Reference Guirao, Montesinos and Zizler16].
As in the case of
![]() $(1+)$
-separated or
$(1+)$
-separated or
![]() $(1+\varepsilon )$
-separated sets, the existence of infinite or uncountable equilateral sets (by the above argument of Terenzi one may assume that such sets are subsets of the unit sphere) was proved by various authors for many particular classes of Banach spaces. For example, infinite equilateral sets exist in any Banach space which contains an isomorphic copy of
$(1+\varepsilon )$
-separated sets, the existence of infinite or uncountable equilateral sets (by the above argument of Terenzi one may assume that such sets are subsets of the unit sphere) was proved by various authors for many particular classes of Banach spaces. For example, infinite equilateral sets exist in any Banach space which contains an isomorphic copy of
![]() $c_0$
[Reference Mercourakis and Vassiliadis37] or any uniformly smooth space [Reference Freeman, Odell, Sari and Schlumprecht10]. However, in contrast to the case of
$c_0$
[Reference Mercourakis and Vassiliadis37] or any uniformly smooth space [Reference Freeman, Odell, Sari and Schlumprecht10]. However, in contrast to the case of
![]() $(1+)$
-separated sets, there are infinite-dimensional Banach spaces with no infinite equilateral subsets [Reference Terenzi48, Reference Terenzi47, Reference Glakousakis and Mercourakis11]. Uncountable equilateral sets in nonseparable Banach spaces have been investigated as well, for example, in [Reference Cúth, Kurka and Vejnar5, Reference Koszmider27, Reference Mercourakis and Vassiliadis37, Reference Mercourakis and Vassiliadis38]. Also the strict convexity of the norm of our example should be compared with the results saying that the unit sphere of an infinite-dimensional uniformly convex space admits a
$(1+)$
-separated sets, there are infinite-dimensional Banach spaces with no infinite equilateral subsets [Reference Terenzi48, Reference Terenzi47, Reference Glakousakis and Mercourakis11]. Uncountable equilateral sets in nonseparable Banach spaces have been investigated as well, for example, in [Reference Cúth, Kurka and Vejnar5, Reference Koszmider27, Reference Mercourakis and Vassiliadis37, Reference Mercourakis and Vassiliadis38]. Also the strict convexity of the norm of our example should be compared with the results saying that the unit sphere of an infinite-dimensional uniformly convex space admits a
![]() $(1+\varepsilon )$
-separated set of the cardinality equal to the density of the space [Reference van Neerven40], Proposition 4.16 of [Reference Hájek, Kania and Russo19].
$(1+\varepsilon )$
-separated set of the cardinality equal to the density of the space [Reference van Neerven40], Proposition 4.16 of [Reference Hájek, Kania and Russo19].
As stressed in [Reference Hájek, Kania and Russo19],
![]() $(1+)$
-separated subsets of the sphere are related to Auerbach bases. Recall that for a Banach space
$(1+)$
-separated subsets of the sphere are related to Auerbach bases. Recall that for a Banach space
![]() $\mathcal {X}$
the system
$\mathcal {X}$
the system
![]() $(x_i, x^*_i)_{i\in \mathcal {I}}\subseteq \mathcal {X}\times \mathcal {X}^*$
is called a biorthogonal system when
$(x_i, x^*_i)_{i\in \mathcal {I}}\subseteq \mathcal {X}\times \mathcal {X}^*$
is called a biorthogonal system when
![]() $x^*_j(x_i)=0$
if
$x^*_j(x_i)=0$
if
![]() $i\not =j$
and
$i\not =j$
and
![]() $x^*_i(x_i)=1$
for each
$x^*_i(x_i)=1$
for each
![]() $i, j\in I$
. It is called an Auerbach system if it is biorthogonal and
$i, j\in I$
. It is called an Auerbach system if it is biorthogonal and
![]() $\|x_i\|=1=\|x^*_i\|$
for every
$\|x_i\|=1=\|x^*_i\|$
for every
![]() $i\in I$
. It is clear that the elements of
$i\in I$
. It is clear that the elements of
![]() $\mathcal {X}$
in an Auerbach system
$\mathcal {X}$
in an Auerbach system
![]() $(x_i, x^*_i)_{i\in \mathcal {I}}$
form a
$(x_i, x^*_i)_{i\in \mathcal {I}}$
form a
![]() $1$
-separated subset of the unit sphere as
$1$
-separated subset of the unit sphere as
![]() $\|x_i-x_j\|\geq |x_i(x_i-x_j)|=|x_i^*(x_i)|=1$
for any distinct
$\|x_i-x_j\|\geq |x_i(x_i-x_j)|=|x_i^*(x_i)|=1$
for any distinct
![]() $i, j\in I$
. Thus, Theorem 1 yields the following:
$i, j\in I$
. Thus, Theorem 1 yields the following:
Theorem 3. There is a (strictly convex) Banach space of density continuum with no uncountable Auerbach system.
A Banach space with this property was previously only constructed under the assumption of the continuum hypothesis CH in [Reference Hájek, Kania and Russo19] (in fact, this is a renorming of
![]() $c_0(\omega _1)$
so WLD, the property not shared by our space). By a result of Day, every separable Banach space admits an infinite Auerbach system [Reference Day6]. Constructions of Banach spaces of density continuum with no fundamental Auerbach systems were presented in [Reference Godun13, Reference Godun14, Reference Pličko43, Reference Godun, Lin and Troyanski15].
$c_0(\omega _1)$
so WLD, the property not shared by our space). By a result of Day, every separable Banach space admits an infinite Auerbach system [Reference Day6]. Constructions of Banach spaces of density continuum with no fundamental Auerbach systems were presented in [Reference Godun13, Reference Godun14, Reference Pličko43, Reference Godun, Lin and Troyanski15].
Our Banach space is an equivalent renorming
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
of the subspace
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
of the subspace
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
of
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
of
![]() $\ell _\infty $
which is spanned by
$\ell _\infty $
which is spanned by
![]() $c_0$
and characteristic functions of elements of an uncountable almost disjoint family
$c_0$
and characteristic functions of elements of an uncountable almost disjoint family
![]() $\mathcal {A}$
of infinite subsets of
$\mathcal {A}$
of infinite subsets of
![]() $\mathbb {N}$
. Recall that
$\mathbb {N}$
. Recall that
![]() $\mathcal {A}\subseteq \wp (\mathbb {N})$
is called almost disjoint if
$\mathcal {A}\subseteq \wp (\mathbb {N})$
is called almost disjoint if
![]() $A\cap A'$
is finite for any distinct
$A\cap A'$
is finite for any distinct
![]() $A, A'\in \mathcal {A}$
. Such spaces
$A, A'\in \mathcal {A}$
. Such spaces
![]() $\mathcal {X}_{\mathcal {A}}$
were first considered by Johnson and Lindenstrauss in [Reference Johnson and Lindenstrauss23, Reference Johnson and Lindenstrauss24]. The renorming
$\mathcal {X}_{\mathcal {A}}$
were first considered by Johnson and Lindenstrauss in [Reference Johnson and Lindenstrauss23, Reference Johnson and Lindenstrauss24]. The renorming
![]() $\|\ \|_T$
is obtained in a standard way using a bounded injective operator
$\|\ \|_T$
is obtained in a standard way using a bounded injective operator
![]() $T:\ell _\infty \rightarrow \ell _2$
(see Section 2.3). As is well known, such a space
$T:\ell _\infty \rightarrow \ell _2$
(see Section 2.3). As is well known, such a space
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
is isometric to the space of the form
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
is isometric to the space of the form
![]() $C_0(K_{\mathcal {A}})$
, where
$C_0(K_{\mathcal {A}})$
, where
![]() $K_{\mathcal {A}}$
is locally compact, totally disconnected, scattered, separable Hausdorff space known as
$K_{\mathcal {A}}$
is locally compact, totally disconnected, scattered, separable Hausdorff space known as
![]() $\Psi $
-space or Mrówka-Isbell space or Alexandroff–Urysohn space (see, e.g., [Reference Hrušák21, Reference Koszmider and Laustsen28]). In particular, it is
$\Psi $
-space or Mrówka-Isbell space or Alexandroff–Urysohn space (see, e.g., [Reference Hrušák21, Reference Koszmider and Laustsen28]). In particular, it is
![]() $c_0$
-saturated (by [Reference Pełczyński and Semadeni42]) so admits infinite equilateral sets by [Reference Mercourakis and Vassiliadis37]. The main point, which actually allows one to conclude directly the previous theorems, is to obtain the behaviour of separated sets of the unit sphere as in
$c_0$
-saturated (by [Reference Pełczyński and Semadeni42]) so admits infinite equilateral sets by [Reference Mercourakis and Vassiliadis37]. The main point, which actually allows one to conclude directly the previous theorems, is to obtain the behaviour of separated sets of the unit sphere as in
![]() $c_0(\Gamma )$
and at the same time to have the underlying locally compact space separable (which allows the construction an injective operator from
$c_0(\Gamma )$
and at the same time to have the underlying locally compact space separable (which allows the construction an injective operator from
![]() $C(K_{\mathcal {A}})$
into the separable
$C(K_{\mathcal {A}})$
into the separable
![]() $\ell _2$
). This is summarized in the following theorem which is proved by applying Lemma 12 and Proposition 15:
$\ell _2$
). This is summarized in the following theorem which is proved by applying Lemma 12 and Proposition 15:
Theorem 4. There is a separable locally compact Hausdorff space K of weight continuum such that for every
![]() $\varepsilon>0$
and every subset
$\varepsilon>0$
and every subset
![]() $\mathcal {Y}$
of the unit sphere of
$\mathcal {Y}$
of the unit sphere of
![]() $C_0(K)$
of a regular uncountable cardinality there is a subset
$C_0(K)$
of a regular uncountable cardinality there is a subset
![]() $\mathcal {Z}\subseteq \mathcal {Y}$
of the same cardinality which is
$\mathcal {Z}\subseteq \mathcal {Y}$
of the same cardinality which is
![]() $(1+\varepsilon )$
-concentrated.
$(1+\varepsilon )$
-concentrated.
To obtain the above property of the space
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
and consequently the properties of its renorming
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
and consequently the properties of its renorming
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
we need some special property of the almost disjoint family
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
we need some special property of the almost disjoint family
![]() $\mathcal {A}$
. A known property that is sufficient for us is the
$\mathcal {A}$
. A known property that is sufficient for us is the
![]() $\mathbb {R}$
-embeddability of
$\mathbb {R}$
-embeddability of
![]() $\mathcal {A}$
(Definition 11). On the other hand, we show that certain almost disjoint families which are not
$\mathcal {A}$
(Definition 11). On the other hand, we show that certain almost disjoint families which are not
![]() $\mathbb {R}$
-embeddable, known as Luzin families (Definition 18), induce the Banach space
$\mathbb {R}$
-embeddable, known as Luzin families (Definition 18), induce the Banach space
![]() $\mathcal {X}_{\mathcal {A}}$
such that the sphere of
$\mathcal {X}_{\mathcal {A}}$
such that the sphere of
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
admits an uncountable
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
admits an uncountable
![]() $2$
-equilateral subset (Proposition 20) and the sphere of
$2$
-equilateral subset (Proposition 20) and the sphere of
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
admits an uncountable
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
admits an uncountable
![]() $(2-\varepsilon )$
-separated subset for any
$(2-\varepsilon )$
-separated subset for any
![]() $\varepsilon>0$
(Proposition 21). For more on
$\varepsilon>0$
(Proposition 21). For more on
![]() $\mathbb {R}$
-embeddability, see [Reference Guzmán, Hrušák and Koszmider17]. Note that A. Dow showed in [Reference Dow8] that assuming PFA (the proper forcing axiom) every maximal almost disjoint family contains a Luzin subfamily. However,
$\mathbb {R}$
-embeddability, see [Reference Guzmán, Hrušák and Koszmider17]. Note that A. Dow showed in [Reference Dow8] that assuming PFA (the proper forcing axiom) every maximal almost disjoint family contains a Luzin subfamily. However,
![]() $\mathbb {R}$
-embeddable families of cardinality continuum are abundant and elementary to construct with no additional set-theoretic assumptions (like Luzin families of cardinality
$\mathbb {R}$
-embeddable families of cardinality continuum are abundant and elementary to construct with no additional set-theoretic assumptions (like Luzin families of cardinality
![]() $\omega _1$
).
$\omega _1$
).
Finally, let us comment on the isomorphic theory structure of our spaces (For the Kottman constant in the isomorphic context, see [Reference Castillo, González, Kania and Papini4]). Using the arguments of Section 5 of [Reference Cabello Sánchez, Castillo, Marciszewski, Plebanek and Salguero-Alarcón2] (cf. [Reference Marciszewski and Pol35]) one can see that there are
![]() $2^{2^\omega }$
pairwise nonisomorphic spaces satisfying Theorem 1. It should be clear that the almost disjoint family of branches of the Cantor tree is
$2^{2^\omega }$
pairwise nonisomorphic spaces satisfying Theorem 1. It should be clear that the almost disjoint family of branches of the Cantor tree is
![]() $\mathbb {R}$
-embeddable and such families are Borel in the product topology on
$\mathbb {R}$
-embeddable and such families are Borel in the product topology on
![]() $2^{\mathbb {N}}$
(see, e.g., Lemma 30 of [Reference Koszmider and Laustsen28]), so it follows from the results of [Reference Marciszewski and Pol36] that the spaces
$2^{\mathbb {N}}$
(see, e.g., Lemma 30 of [Reference Koszmider and Laustsen28]), so it follows from the results of [Reference Marciszewski and Pol36] that the spaces
![]() $\mathcal {X}_{\mathcal {A}}$
satisfying Theorem 1 can be isomorphically of the form
$\mathcal {X}_{\mathcal {A}}$
satisfying Theorem 1 can be isomorphically of the form
![]() $C(K_{\mathcal {A}})$
, where
$C(K_{\mathcal {A}})$
, where
![]() $K_{\mathcal {A}}$
is a Rosenthal compact space. The results of [Reference Godefroy and Talagrand12] imply that such spaces are representable in the sense of that paper, so they should be considered relatively constructive and nonpathological.
$K_{\mathcal {A}}$
is a Rosenthal compact space. The results of [Reference Godefroy and Talagrand12] imply that such spaces are representable in the sense of that paper, so they should be considered relatively constructive and nonpathological.
![]() $\mathcal {X}_{\mathcal {A}}$
in the norm
$\mathcal {X}_{\mathcal {A}}$
in the norm
![]() $\|\ \|_\infty $
admits a
$\|\ \|_\infty $
admits a
![]() $1$
-equilateral set of cardinality continuum which is an Auerbach system (just characteristic functions of the elements of the almost disjoint family
$1$
-equilateral set of cardinality continuum which is an Auerbach system (just characteristic functions of the elements of the almost disjoint family
![]() $\mathcal {A}$
). Although, as mentioned above, there are many nonisomorphic Banach spaces of the form
$\mathcal {A}$
). Although, as mentioned above, there are many nonisomorphic Banach spaces of the form
![]() $\mathcal {X}_{\mathcal {A}}$
for an almost disjoint families
$\mathcal {X}_{\mathcal {A}}$
for an almost disjoint families
![]() $\mathcal {A}$
, under Martin’s axiom MA and the negation of CH all spaces
$\mathcal {A}$
, under Martin’s axiom MA and the negation of CH all spaces
![]() $\mathcal {X}_{\mathcal {A}}$
are pairwise isomorphic for
$\mathcal {X}_{\mathcal {A}}$
are pairwise isomorphic for
![]() $\mathcal {A}$
of cardinality
$\mathcal {A}$
of cardinality
![]() $\omega _1$
, in particular
$\omega _1$
, in particular
![]() $\mathcal {X}_{\mathcal {A}}$
can be isomorphic to
$\mathcal {X}_{\mathcal {A}}$
can be isomorphic to
![]() $\mathcal {X}_{\mathcal {A}'}$
with
$\mathcal {X}_{\mathcal {A}'}$
with
![]() $\mathcal {A}$
being
$\mathcal {A}$
being
![]() $\mathbb {R}$
-embeddable and
$\mathbb {R}$
-embeddable and
![]() $\mathcal {A}'$
being Luzin ([Reference Cabello Sánchez, Castillo, Marciszewski, Plebanek and Salguero-Alarcón2]). This, for example, provides equivalent renormings of
$\mathcal {A}'$
being Luzin ([Reference Cabello Sánchez, Castillo, Marciszewski, Plebanek and Salguero-Alarcón2]). This, for example, provides equivalent renormings of
![]() $(\mathcal {X}_A, \|\ \|_\infty )$
for any Luzin family
$(\mathcal {X}_A, \|\ \|_\infty )$
for any Luzin family
![]() $\mathcal {A}$
which satisfy Theorem 1. In fact, at least consistently, every nonseparable Banach space can be renormed so that the new unit sphere admits uncountable
$\mathcal {A}$
which satisfy Theorem 1. In fact, at least consistently, every nonseparable Banach space can be renormed so that the new unit sphere admits uncountable
![]() $2$
-equilateral sets (Theorem 3 [Reference Mercourakis and Vassiliadis37]). It is unknown at the present moment if this can be proved in ZFC alone.
$2$
-equilateral sets (Theorem 3 [Reference Mercourakis and Vassiliadis37]). It is unknown at the present moment if this can be proved in ZFC alone.
2 Preliminaries and terminology
2.1 Notation
The notation attempts to be standard, for unexplained terminology see [Reference Hájek, Montesinos Santalucía, Vanderwerff and Zizler18]. In particular
![]() $C(K)$
denotes the set of all continuous functions on a compact Hausdorff space K and
$C(K)$
denotes the set of all continuous functions on a compact Hausdorff space K and
![]() $C_0(K)$
denotes all continuous functions f on a locally compact Hausdorff K such that for each
$C_0(K)$
denotes all continuous functions f on a locally compact Hausdorff K such that for each
![]() $\varepsilon>0$
there is a compact
$\varepsilon>0$
there is a compact
![]() $L\subset K$
such that
$L\subset K$
such that
![]() $|f(x)|<\varepsilon $
for all
$|f(x)|<\varepsilon $
for all
![]() $x\in K\setminus L$
. Both of these types of linear spaces are considered as Banach spaces with the supremum norm which is denoted by
$x\in K\setminus L$
. Both of these types of linear spaces are considered as Banach spaces with the supremum norm which is denoted by
![]() $\|\ \|_\infty $
. The notation
$\|\ \|_\infty $
. The notation
![]() $1_A$
denotes the characteristic function of a set A. When
$1_A$
denotes the characteristic function of a set A. When
![]() $\mathcal {Y}$
is a subset of a Banach space,
$\mathcal {Y}$
is a subset of a Banach space,
![]() $\overline {span}(\mathcal {Y})$
denotes the norm closure of the linear span of
$\overline {span}(\mathcal {Y})$
denotes the norm closure of the linear span of
![]() $\mathcal {Y}$
. The density of an infinite-dimensional Banach space is the minimal cardinality of a norm dense subset of the space. By
$\mathcal {Y}$
. The density of an infinite-dimensional Banach space is the minimal cardinality of a norm dense subset of the space. By
![]() $\omega _1$
, we mean the first uncountable cardinal. All almost disjoint families of subsets of
$\omega _1$
, we mean the first uncountable cardinal. All almost disjoint families of subsets of
![]() $\mathbb {N}$
considered in this paper are uncountable and consist of infinite sets. A cardinal
$\mathbb {N}$
considered in this paper are uncountable and consist of infinite sets. A cardinal
![]() $\kappa $
is said to be of uncountable cofinality if the union of countably many sets of cardinalities smaller than
$\kappa $
is said to be of uncountable cofinality if the union of countably many sets of cardinalities smaller than
![]() $\kappa $
has cardinality smaller than
$\kappa $
has cardinality smaller than
![]() $\kappa $
. If A is a set, then
$\kappa $
. If A is a set, then
![]() $[A]^2$
denotes the family of all two-element subsets of A. The cardinals like
$[A]^2$
denotes the family of all two-element subsets of A. The cardinals like
![]() $\omega _1$
or the continuum are of uncountable cofinality ([Reference Jech22]). If
$\omega _1$
or the continuum are of uncountable cofinality ([Reference Jech22]). If
![]() $(x_n)_{n\in \mathbb {N}}$
is a sequence of reals and
$(x_n)_{n\in \mathbb {N}}$
is a sequence of reals and
![]() $A\subseteq \mathbb {N}$
is infinite by
$A\subseteq \mathbb {N}$
is infinite by
![]() $\lim _{n\in A}x_n$
we mean
$\lim _{n\in A}x_n$
we mean
![]() $\lim _{k\rightarrow \infty }x_{n_k}$
, where
$\lim _{k\rightarrow \infty }x_{n_k}$
, where
![]() $({n_k})_{k\in \mathbb {N}}$
is any (bijective) renumeration of A.
$({n_k})_{k\in \mathbb {N}}$
is any (bijective) renumeration of A.
2.2 Banach spaces
 $\mathcal {X}_{\mathcal {A}}$
$\mathcal {X}_{\mathcal {A}}$
Given an infinite almost disjoint family
![]() $\mathcal {A}$
of infinite subsets of
$\mathcal {A}$
of infinite subsets of
![]() $\mathbb {N}$
, we consider the subspace of
$\mathbb {N}$
, we consider the subspace of
![]() $(\ell _\infty , \|\ \|_\infty )$
defined by
$(\ell _\infty , \|\ \|_\infty )$
defined by
Note that for a fixed
![]() $A_0\in \mathcal {A}$
the set
$A_0\in \mathcal {A}$
the set
is a closed (in the
![]() $\|\ \|_\infty $
-norm) linear subspace of
$\|\ \|_\infty $
-norm) linear subspace of
![]() $\ell _\infty $
. As for every
$\ell _\infty $
. As for every
![]() $A_0\in \mathcal {A}$
all the generators
$A_0\in \mathcal {A}$
all the generators
![]() $\{1_A: A\in \mathcal {A}\}\cup c_0$
of
$\{1_A: A\in \mathcal {A}\}\cup c_0$
of
![]() $\mathcal {X}_{\mathcal {A}}$
are in this space, it follows that the entire
$\mathcal {X}_{\mathcal {A}}$
are in this space, it follows that the entire
![]() $\mathcal {X}_{\mathcal {A}}$
is contained in every
$\mathcal {X}_{\mathcal {A}}$
is contained in every
![]() $\ell _\infty ^{A}$
for
$\ell _\infty ^{A}$
for
![]() $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
.
Lemma 5. Suppose that
![]() $\mathcal {A}$
is an almost disjoint family of infinite subsets of
$\mathcal {A}$
is an almost disjoint family of infinite subsets of
![]() $\mathbb {N}$
. Let
$\mathbb {N}$
. Let
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $g\in c_0$
,
$g\in c_0$
,
![]() $A_1, \dots , A_k\in \mathcal {A}$
be distinct,
$A_1, \dots , A_k\in \mathcal {A}$
be distinct,
![]() $q_1, \dots q_k\in \mathbb {R}$
and
$q_1, \dots q_k\in \mathbb {R}$
and
Then for every
![]() $1\leq j \leq k$
, we have
$1\leq j \leq k$
, we have
![]() $\lim _{n\in A_j}f(n)=q_j$
.
$\lim _{n\in A_j}f(n)=q_j$
.
Proof. We have
![]() $\lim _{n\in A_j}g(n)=0$
as
$\lim _{n\in A_j}g(n)=0$
as
![]() $g\in c_0$
and
$g\in c_0$
and
![]() $\lim _{n\in A_j}1_{A_i}(n)=0$
for
$\lim _{n\in A_j}1_{A_i}(n)=0$
for
![]() $i\not =j$
since
$i\not =j$
since
![]() $A_i\cap A_j$
is finite.
$A_i\cap A_j$
is finite.
2.3 Equivalent renormings induced by bounded operators
Recall that two norms
![]() $\|\ \|$
and
$\|\ \|$
and
![]() $\|\ \|'$
on a Banach space
$\|\ \|'$
on a Banach space
![]() $\mathcal {X}$
are equivalent if the identity operator between
$\mathcal {X}$
are equivalent if the identity operator between
![]() $(\mathcal {X}, \|\ \|)$
and
$(\mathcal {X}, \|\ \|)$
and
![]() $(\mathcal {X}, \|\ \|')$
is an isomorphism, that is, when there are positive constants
$(\mathcal {X}, \|\ \|')$
is an isomorphism, that is, when there are positive constants
![]() $c, C$
such that
$c, C$
such that
![]() $c\| x\|\leq \|x \|'\leq C\| x\|$
for every
$c\| x\|\leq \|x \|'\leq C\| x\|$
for every
![]() $x\in \mathcal {X}$
. For more on renormings, see [Reference Deville, Godefroy and Zizler7]. It is clear that if
$x\in \mathcal {X}$
. For more on renormings, see [Reference Deville, Godefroy and Zizler7]. It is clear that if
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
are Banach spaces with norms
$\mathcal {Y}$
are Banach spaces with norms
![]() $\|\ \|_{\mathcal {X}}$
and
$\|\ \|_{\mathcal {X}}$
and
![]() $\|\ \|_{\mathcal {Y}}$
, respectively, and
$\|\ \|_{\mathcal {Y}}$
, respectively, and
![]() $T:\mathcal {X}\rightarrow \mathcal {Y}$
is a bounded linear operator. Then
$T:\mathcal {X}\rightarrow \mathcal {Y}$
is a bounded linear operator. Then
is a norm on
![]() $\mathcal {X}$
which is equivalent to the norm
$\mathcal {X}$
which is equivalent to the norm
![]() $\|\ \|_{\mathcal {X}}$
. In this paper, besides the supremum norm
$\|\ \|_{\mathcal {X}}$
. In this paper, besides the supremum norm
![]() $\|\ \|_\infty $
, we will consider norms of the form
$\|\ \|_\infty $
, we will consider norms of the form
![]() $\|\ \|_T$
. Recall that a norm
$\|\ \|_T$
. Recall that a norm
![]() $\| \ \|$
on a Banach space
$\| \ \|$
on a Banach space
![]() $\mathcal {X}$
is called strictly convex if
$\mathcal {X}$
is called strictly convex if
![]() $\|x+y\|=\|x\|+\|y\|$
for
$\|x+y\|=\|x\|+\|y\|$
for
![]() $x, y\in \mathcal {X}\setminus \{0\}$
implies that
$x, y\in \mathcal {X}\setminus \{0\}$
implies that
![]() $x=\lambda y$
for some
$x=\lambda y$
for some
![]() $\lambda> 0$
. An example of a strictly convex norm is the standard
$\lambda> 0$
. An example of a strictly convex norm is the standard
![]() $\| \ \|_2$
norm on
$\| \ \|_2$
norm on
![]() $\ell _2$
.
$\ell _2$
.
Lemma 6. Suppose that
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
are Banach spaces. If
$\mathcal {Y}$
are Banach spaces. If
![]() $T: \mathcal {X}\rightarrow \mathcal {Y}$
is an injective bounded linear operator,
$T: \mathcal {X}\rightarrow \mathcal {Y}$
is an injective bounded linear operator,
![]() $(\mathcal {Y}, \|\ \|_{\mathcal {Y}})$
is strictly convex, then
$(\mathcal {Y}, \|\ \|_{\mathcal {Y}})$
is strictly convex, then
![]() $(\mathcal {X}, \|\ \|_T)$
is strictly convex.
$(\mathcal {X}, \|\ \|_T)$
is strictly convex.
Proof. For nonzero
![]() $x, y\in \mathcal {X}$
, by the triangle inequality, the condition
$x, y\in \mathcal {X}$
, by the triangle inequality, the condition
implies that
![]() $\|x+y\|_{\mathcal {X}}=\|x\|_{\mathcal {X}}+\|y\|_{\mathcal {X}}$
and
$\|x+y\|_{\mathcal {X}}=\|x\|_{\mathcal {X}}+\|y\|_{\mathcal {X}}$
and
![]() $\|T(x)+T(y)\|_{\mathcal {Y}}=\|T(x)\|_{\mathcal {Y}}+\|T(y)\|_{\mathcal {Y}}$
. The latter implies
$\|T(x)+T(y)\|_{\mathcal {Y}}=\|T(x)\|_{\mathcal {Y}}+\|T(y)\|_{\mathcal {Y}}$
. The latter implies
![]() $T(x)=\lambda T(y)$
for some
$T(x)=\lambda T(y)$
for some
![]() $\lambda> 0$
, which gives
$\lambda> 0$
, which gives
![]() $x=\lambda y$
since T is injective.
$x=\lambda y$
since T is injective.
Lemma 7. There is an injective bounded linear operator
![]() $T:\ell _\infty \rightarrow \ell _2$
. In particular, the equivalent renorming
$T:\ell _\infty \rightarrow \ell _2$
. In particular, the equivalent renorming
![]() $(\ell _\infty , \|\ \|_T)$
is strictly convex.
$(\ell _\infty , \|\ \|_T)$
is strictly convex.
Proof. Consider
![]() $T:\ell _\infty \rightarrow \ell _2$
given by
$T:\ell _\infty \rightarrow \ell _2$
given by
![]() $\|f\|_\infty \leq \|f\|_\infty +\|T(f)\|_2= \|f\|_\infty +\sqrt {\sum _{n\in \mathbb {N}}{f(n)^2\over 2^{n}}}\leq (1+\sqrt 2)\| f\|_\infty $
.
$\|f\|_\infty \leq \|f\|_\infty +\|T(f)\|_2= \|f\|_\infty +\sqrt {\sum _{n\in \mathbb {N}}{f(n)^2\over 2^{n}}}\leq (1+\sqrt 2)\| f\|_\infty $
.
Lemma 8. Suppose that
![]() $\kappa $
is a cardinal of uncountable cofinality and
$\kappa $
is a cardinal of uncountable cofinality and
![]() $\mathcal {Y}$
is a subset of cardinality
$\mathcal {Y}$
is a subset of cardinality
![]() $\kappa $
of a separable Banach space
$\kappa $
of a separable Banach space
![]() $\mathcal {X}$
. Then for every
$\mathcal {X}$
. Then for every
![]() $\varepsilon>0$
there is
$\varepsilon>0$
there is
![]() $\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
$\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
![]() $\kappa $
such that
$\kappa $
such that
![]() $\|y-y'\|\leq \varepsilon $
for every
$\|y-y'\|\leq \varepsilon $
for every
![]() $y, y'\in \mathcal {Y}'$
.
$y, y'\in \mathcal {Y}'$
.
Proof. Let
![]() $\{x_n: n\in \mathbb {N}\}$
be norm dense countable subset of
$\{x_n: n\in \mathbb {N}\}$
be norm dense countable subset of
![]() $\mathcal {X}$
. Balls of diameter
$\mathcal {X}$
. Balls of diameter
![]() $\varepsilon $
with the centers in the points
$\varepsilon $
with the centers in the points
![]() $x_n$
cover
$x_n$
cover
![]() $\mathcal {X}$
and so cover
$\mathcal {X}$
and so cover
![]() $\mathcal {Y}$
. By the uncountable cofinality of
$\mathcal {Y}$
. By the uncountable cofinality of
![]() $\kappa $
, one of the balls must contain
$\kappa $
, one of the balls must contain
![]() $\kappa $
elements of
$\kappa $
elements of
![]() $\mathcal {Y}$
.
$\mathcal {Y}$
.
Lemma 9. Suppose that
![]() $0<a\leq \|x\|\leq \|x'\|\leq b<1$
for some
$0<a\leq \|x\|\leq \|x'\|\leq b<1$
for some
![]() $a, b\in \mathbb {R}$
and
$a, b\in \mathbb {R}$
and
![]() $x, x'$
in a Banach space
$x, x'$
in a Banach space
![]() $\mathcal {X}$
. Then
$\mathcal {X}$
. Then
 $$ \begin{align*}\|x-x'\|\leq b\Bigg\|{x\over{\|x\|}}-{x'\over{\|x'\|}}\Bigg\|+(b-a)\end{align*} $$
$$ \begin{align*}\|x-x'\|\leq b\Bigg\|{x\over{\|x\|}}-{x'\over{\|x'\|}}\Bigg\|+(b-a)\end{align*} $$
Proof.
 $$ \begin{align*}\leq \|x\|\Bigg\|{x\over{\|x\|}}-{x'\over{\|x'\|}}\Bigg\| +\Bigg|{\|x\|\over{\|x'\|}} -1 \Bigg|\|x'\|\leq\end{align*} $$
$$ \begin{align*}\leq \|x\|\Bigg\|{x\over{\|x\|}}-{x'\over{\|x'\|}}\Bigg\| +\Bigg|{\|x\|\over{\|x'\|}} -1 \Bigg|\|x'\|\leq\end{align*} $$
 $$ \begin{align*}\leq b\Bigg\|{x\over{\|x\|}}-{x'\over{\|x'\|}}\Bigg\|+(1-a/b)b.\\[-36pt]\end{align*} $$
$$ \begin{align*}\leq b\Bigg\|{x\over{\|x\|}}-{x'\over{\|x'\|}}\Bigg\|+(1-a/b)b.\\[-36pt]\end{align*} $$
The following reduction result allows us to infer the main properties of the final space
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
as stated in Theorem 1 from the properties of the space
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
as stated in Theorem 1 from the properties of the space
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
which are proved in Proposition 15.
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
which are proved in Proposition 15.
Proposition 10. Suppose that
![]() $\mathcal X$
is a nonseparable Banach space and
$\mathcal X$
is a nonseparable Banach space and
![]() $\kappa $
is a cardinal of uncountable cofinality such that for every subset
$\kappa $
is a cardinal of uncountable cofinality such that for every subset
![]() $\mathcal {Y}$
of the unit sphere of
$\mathcal {Y}$
of the unit sphere of
![]() $(\mathcal {X}, \|\ \|_{\mathcal {X}})$
of cardinality
$(\mathcal {X}, \|\ \|_{\mathcal {X}})$
of cardinality
![]() $\kappa $
and every
$\kappa $
and every
![]() $\varepsilon>0$
there is
$\varepsilon>0$
there is
![]() $\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
$\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
![]() $\kappa $
which is
$\kappa $
which is
![]() $(1+\varepsilon )$
-concentrated. If
$(1+\varepsilon )$
-concentrated. If
![]() $T: \mathcal {X}\rightarrow \mathcal {Z}$
is a bounded linear injective operator into a Banach space
$T: \mathcal {X}\rightarrow \mathcal {Z}$
is a bounded linear injective operator into a Banach space
![]() $\mathcal {Z}$
with separable range, then
$\mathcal {Z}$
with separable range, then
![]() $(\mathcal {X}, \|\ \|_T)$
has the following property: For every subset
$(\mathcal {X}, \|\ \|_T)$
has the following property: For every subset
![]() $\mathcal {Y}$
of the unit sphere of
$\mathcal {Y}$
of the unit sphere of
![]() $(\mathcal {X}, \|\ \|_T)$
of cardinality
$(\mathcal {X}, \|\ \|_T)$
of cardinality
![]() $\kappa $
, there is
$\kappa $
, there is
![]() $\delta>0$
and
$\delta>0$
and
![]() $\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
$\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
![]() $\kappa $
which is
$\kappa $
which is
![]() $(1-\delta )$
-concentrated.
$(1-\delta )$
-concentrated.
Proof. Let
![]() $\mathcal {Y}$
be a subset of the unit sphere of
$\mathcal {Y}$
be a subset of the unit sphere of
![]() $(\mathcal {X}, \|\ \|_T)$
of cardinality
$(\mathcal {X}, \|\ \|_T)$
of cardinality
![]() $\kappa $
. As T is injective, we have
$\kappa $
. As T is injective, we have
![]() $0<\|y\|_{\mathcal {X}}<\|y\|_T=1$
for every
$0<\|y\|_{\mathcal {X}}<\|y\|_T=1$
for every
![]() $y\in \mathcal {Y}$
. The interval
$y\in \mathcal {Y}$
. The interval
![]() $(0,1)$
can be covered by intervals of the form
$(0,1)$
can be covered by intervals of the form
![]() $(q-(1-q)/4, q)$
for rationals q satisfying
$(q-(1-q)/4, q)$
for rationals q satisfying
![]() $0<q<1$
. As
$0<q<1$
. As
![]() $\kappa $
has uncountable cofinality by passing to a subset of cardinality
$\kappa $
has uncountable cofinality by passing to a subset of cardinality
![]() $\kappa $
, we may assume that there is a rational
$\kappa $
, we may assume that there is a rational
![]() $0<q<1$
such that
$0<q<1$
such that
for every
![]() $y\in \mathcal {Y}$
. Now, apply the property of
$y\in \mathcal {Y}$
. Now, apply the property of
![]() $\mathcal {X}$
with the norm
$\mathcal {X}$
with the norm
![]() $\|\ \|_{\mathcal {X}}$
to
$\|\ \|_{\mathcal {X}}$
to
![]() $\{y/\|y\|_{\mathcal {X}}: y\in \mathcal {Y}\}$
and
$\{y/\|y\|_{\mathcal {X}}: y\in \mathcal {Y}\}$
and
![]() $\varepsilon =(1-q)/4q$
obtaining
$\varepsilon =(1-q)/4q$
obtaining
![]() $\mathcal {X}'\subseteq \{y/\|y\|_{\mathcal {X}}: y\in \mathcal {Y}\}$
of cardinality
$\mathcal {X}'\subseteq \{y/\|y\|_{\mathcal {X}}: y\in \mathcal {Y}\}$
of cardinality
![]() $\kappa $
such that
$\kappa $
such that
![]() $\mathcal {X}'$
is
$\mathcal {X}'$
is
![]() $(1+\varepsilon )$
-concentrated in the
$(1+\varepsilon )$
-concentrated in the
![]() $\|\ \|_{\mathcal {X}}$
norm. By Lemma 9 for
$\|\ \|_{\mathcal {X}}$
norm. By Lemma 9 for
![]() $a=q-(1-q)/4\leq \|y\|_{\mathcal {X}}\leq \|y'\|_{\mathcal {X}}\leq q=b$
, we obtain that
$a=q-(1-q)/4\leq \|y\|_{\mathcal {X}}\leq \|y'\|_{\mathcal {X}}\leq q=b$
, we obtain that
 $$ \begin{align*}\|y'-y''\|_{\mathcal{X}}\leq q(1+(1-q)/4q)+(1-q)/4=\\= (q+(1-q)/4)+(1-q)/4=q+(1-q)/2\end{align*} $$
$$ \begin{align*}\|y'-y''\|_{\mathcal{X}}\leq q(1+(1-q)/4q)+(1-q)/4=\\= (q+(1-q)/4)+(1-q)/4=q+(1-q)/2\end{align*} $$
for every
![]() $y', y''\in \mathcal {Y}'=\{y\in \mathcal {Y}: y/\|y\|_{\mathcal {X}}\in \mathcal {X}'\}$
. Again using the countable cofinality of
$y', y''\in \mathcal {Y}'=\{y\in \mathcal {Y}: y/\|y\|_{\mathcal {X}}\in \mathcal {X}'\}$
. Again using the countable cofinality of
![]() $\kappa $
and Lemma 8, we find
$\kappa $
and Lemma 8, we find
![]() $\mathcal {Y}''\subseteq \mathcal {Y}'$
of cardinality
$\mathcal {Y}''\subseteq \mathcal {Y}'$
of cardinality
![]() $\kappa $
such that
$\kappa $
such that
![]() $\|T(y)-T(y')\|_{\mathcal {Z}}\leq (1-q)/4$
for all
$\|T(y)-T(y')\|_{\mathcal {Z}}\leq (1-q)/4$
for all
![]() $y, y'\in \mathcal {Y}''$
. So
$y, y'\in \mathcal {Y}''$
. So
obtaining that
![]() $\mathcal {Y}''$
is
$\mathcal {Y}''$
is
![]() $(1-\delta )$
-concentrated for
$(1-\delta )$
-concentrated for
![]() $\delta =(1-q)/4$
as required.
$\delta =(1-q)/4$
as required.
3 Concentration in spheres of Banach spaces
 $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
induced by
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
induced by
 $\mathbb {R}$
-embeddable almost disjoint families
$\mathbb {R}$
-embeddable almost disjoint families
Definition 11. An almost disjoint family
![]() $\mathcal {A}$
of subsets of
$\mathcal {A}$
of subsets of
![]() $\mathbb {N}$
is called
$\mathbb {N}$
is called
![]() $\mathbb {R}$
-embeddable if there is a function
$\mathbb {R}$
-embeddable if there is a function
![]() $\phi :\mathbb {N}\rightarrow \mathbb {R}$
such that the sets
$\phi :\mathbb {N}\rightarrow \mathbb {R}$
such that the sets
![]() $\phi [A]$
for
$\phi [A]$
for
![]() $A\in \mathcal {A}$
are ranges of sequences converging to distinct reals.
$A\in \mathcal {A}$
are ranges of sequences converging to distinct reals.
So
![]() $\mathbb {R}$
-embeddable families of cardinality continuum are examples of perhaps most standard almost disjoint families.
$\mathbb {R}$
-embeddable families of cardinality continuum are examples of perhaps most standard almost disjoint families.
Lemma 12 Folklore
There exist almost disjoint families of infinite subsets of
![]() $\mathbb {N}$
of cardinality continuum which are
$\mathbb {N}$
of cardinality continuum which are
![]() $\mathbb {R}$
-embeddable.
$\mathbb {R}$
-embeddable.
Remark 13. In fact, an almost disjoint family
![]() $\mathcal {A}$
of infinite subsets of
$\mathcal {A}$
of infinite subsets of
![]() $\mathbb {N}$
is
$\mathbb {N}$
is
![]() $\mathbb {R}$
-embeddable if and only if there is an injective
$\mathbb {R}$
-embeddable if and only if there is an injective
![]() $\phi :\mathbb {N}\rightarrow \mathbb {Q}$
such that the sets
$\phi :\mathbb {N}\rightarrow \mathbb {Q}$
such that the sets
![]() $\phi [A]$
for
$\phi [A]$
for
![]() $A\in A$
are ranges of sequences converging to distinct irrational reals. This follows from Lemma 1 and Lemma 2 of [Reference Guzmán, Hrušák and Koszmider17].
$A\in A$
are ranges of sequences converging to distinct irrational reals. This follows from Lemma 1 and Lemma 2 of [Reference Guzmán, Hrušák and Koszmider17].
Lemma 14. Suppose that
![]() $\kappa $
is a cardinal of uncountable cofinality not bigger than continuum,
$\kappa $
is a cardinal of uncountable cofinality not bigger than continuum,
![]() $X\subseteq [0,1]$
is uncountable and that
$X\subseteq [0,1]$
is uncountable and that
![]() $\mathcal {A}=\{A_x: x\in X\}$
is an
$\mathcal {A}=\{A_x: x\in X\}$
is an
![]() $\mathbb {R}$
-embeddable almost disjoint family of infinite subsets of
$\mathbb {R}$
-embeddable almost disjoint family of infinite subsets of
![]() $\mathbb {N}$
. Then given
$\mathbb {N}$
. Then given
-
(1)
 $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
, -
(2) a finite
 $F\subseteq \mathbb {N}$
,
$F\subseteq \mathbb {N}$
, -
(3) a collection
 $\{a_\xi : \xi <\kappa \}$
of pairwise disjoint finite subsets of X with
$\{a_\xi : \xi <\kappa \}$
of pairwise disjoint finite subsets of X with
 $a_\xi =\{x_1^\xi , \ldots , x_k^\xi \}$
(
$a_\xi =\{x_1^\xi , \ldots , x_k^\xi \}$
(
 $x_i^\xi \not =x^\xi _j$
for
$x_i^\xi \not =x^\xi _j$
for
 $1\leq i<j\leq k$
) for any
$1\leq i<j\leq k$
) for any
 $\xi <\kappa $
such that
$\xi <\kappa $
such that  $$ \begin{align*}A_{x_i^\xi}\cap A_{x_j^\xi}\subseteq F\end{align*} $$
$$ \begin{align*}A_{x_i^\xi}\cap A_{x_j^\xi}\subseteq F\end{align*} $$
for any
 $\xi <\kappa $
and any
$\xi <\kappa $
and any
 $1\leq i<j\leq k$
,
$1\leq i<j\leq k$
,
there is a subset
![]() $\Gamma \subseteq \kappa $
of cardinality
$\Gamma \subseteq \kappa $
of cardinality
![]() $\kappa $
such that for every
$\kappa $
such that for every
![]() $\xi ,\eta \in \Gamma $
we have
$\xi ,\eta \in \Gamma $
we have
for every
![]() $1\leq i<j\leq k$
.
$1\leq i<j\leq k$
.
Proof. Let
![]() $\phi :\mathbb {N}\rightarrow \mathbb {R}$
be as in the definition of
$\phi :\mathbb {N}\rightarrow \mathbb {R}$
be as in the definition of
![]() $\mathbb {R}$
-embeddability. By composing it with a homeomorphism from
$\mathbb {R}$
-embeddability. By composing it with a homeomorphism from
![]() $\mathbb {R}$
onto
$\mathbb {R}$
onto
![]() $(0,1)$
, we may assume that
$(0,1)$
, we may assume that
![]() $Y=\phi [\mathbb {N}]\subseteq [0,1]$
. As the properties stated in the lemma do not change if we relabel the elements of
$Y=\phi [\mathbb {N}]\subseteq [0,1]$
. As the properties stated in the lemma do not change if we relabel the elements of
![]() $\mathcal {A}$
, we may assume that
$\mathcal {A}$
, we may assume that
![]() $\phi [A_x]=\{q_n^x: n\in \mathbb {N}\}\subseteq [0,1]\cap Y$
is such that
$\phi [A_x]=\{q_n^x: n\in \mathbb {N}\}\subseteq [0,1]\cap Y$
is such that
![]() $(q_n^x)_{n\in \mathbb {N}}$
converges to x.
$(q_n^x)_{n\in \mathbb {N}}$
converges to x.
Fix
![]() $k\in \mathbb {N}$
and a finite
$k\in \mathbb {N}$
and a finite
![]() $F\subseteq \mathbb {N}$
. Let
$F\subseteq \mathbb {N}$
. Let
![]() $\{a_\xi : \xi <\omega _1\}$
be a collection of pairwise disjoint finite subsets of X with
$\{a_\xi : \xi <\omega _1\}$
be a collection of pairwise disjoint finite subsets of X with
![]() $a_\xi =\{x_1^\xi , \ldots , x_k^\xi \}$
as in the lemma. Using the uncountable cofinality of
$a_\xi =\{x_1^\xi , \ldots , x_k^\xi \}$
as in the lemma. Using the uncountable cofinality of
![]() $\kappa $
, by passing to subset of cardinality
$\kappa $
, by passing to subset of cardinality
![]() $\kappa $
, we may assume that for all
$\kappa $
, we may assume that for all
![]() $\xi <\kappa $
we have
$\xi <\kappa $
we have
![]() $\delta _\xi>\delta $
for some
$\delta _\xi>\delta $
for some
![]() $\delta>0$
, where
$\delta>0$
, where
Now, note that there is
![]() $(x_1, \dots , x_k)\in [0,1]^k$
such that every Euclidean neighbourhood of
$(x_1, \dots , x_k)\in [0,1]^k$
such that every Euclidean neighbourhood of
![]() $(x_1, \dots , x_k)$
contains
$(x_1, \dots , x_k)$
contains
![]() $\kappa $
-many points
$\kappa $
-many points
![]() $(x_1^\xi , \ldots , x_k^\xi )$
for
$(x_1^\xi , \ldots , x_k^\xi )$
for
![]() $\xi <\kappa $
. This is because otherwise we can cover
$\xi <\kappa $
. This is because otherwise we can cover
![]() $[0,1]^k$
by open sets each containing less than
$[0,1]^k$
by open sets each containing less than
![]() $\kappa $
-many of the points
$\kappa $
-many of the points
![]() $(x_1^\xi , \ldots , x_k^\xi )$
, and the existence of a finite subcover would contradict the fact that all k-tuples
$(x_1^\xi , \ldots , x_k^\xi )$
, and the existence of a finite subcover would contradict the fact that all k-tuples
![]() $(x_1^\xi , \ldots , x_k^\xi )$
are distinct as the sets
$(x_1^\xi , \ldots , x_k^\xi )$
are distinct as the sets
![]() $\{x_1^\xi , \ldots , x_k^\xi \}$
are pairwise disjoint.
$\{x_1^\xi , \ldots , x_k^\xi \}$
are pairwise disjoint.
Since
![]() $\delta _\xi>\delta $
for every
$\delta _\xi>\delta $
for every
![]() $\xi <\kappa $
, we have that
$\xi <\kappa $
, we have that
![]() $\min (\{|x_i-x_j|: 1\leq i<j\leq \}\geq \delta $
, and in particular all elements
$\min (\{|x_i-x_j|: 1\leq i<j\leq \}\geq \delta $
, and in particular all elements
![]() $x_i$
for
$x_i$
for
![]() $1\leq i\leq k$
are distinct. Let
$1\leq i\leq k$
are distinct. Let
![]() $I_1, \dots I_k$
be open intervals such that
$I_1, \dots I_k$
be open intervals such that
![]() $x_i\in I_i$
and
$x_i\in I_i$
and
![]() $I_i\cap I_j=\emptyset $
for all
$I_i\cap I_j=\emptyset $
for all
![]() $1\leq i<j\leq k$
. By the choice of
$1\leq i<j\leq k$
. By the choice of
![]() $(x_1, \dots , x_k)$
, there is
$(x_1, \dots , x_k)$
, there is
![]() $\Gamma '\subseteq \kappa $
of cardinality
$\Gamma '\subseteq \kappa $
of cardinality
![]() $\kappa $
such that
$\kappa $
such that
for all
![]() $\xi \in \Gamma '$
and all
$\xi \in \Gamma '$
and all
![]() $1\leq i\leq k$
.
$1\leq i\leq k$
.
Since the sequence
![]() $(q_n^{x_i^\xi })_{n\in \mathbb {N}}$
converges to
$(q_n^{x_i^\xi })_{n\in \mathbb {N}}$
converges to
![]() ${x_i^\xi }$
, for every
${x_i^\xi }$
, for every
![]() $\xi \in \Gamma '$
, there is a sequence
$\xi \in \Gamma '$
, there is a sequence
![]() $(F_1^\xi , \dots F_k^\xi )$
of finite subsets of
$(F_1^\xi , \dots F_k^\xi )$
of finite subsets of
![]() $\mathbb {N}$
such that for each
$\mathbb {N}$
such that for each
![]() $1\leq i\leq k$
we have
$1\leq i\leq k$
we have
-
(1)
 $F_i^\xi \subseteq A_{x^i_\xi }$
$F_i^\xi \subseteq A_{x^i_\xi }$
-
(2)
 $\phi [A_{x^i_\xi }\setminus F_i^\xi ]\subseteq I_i$
.
$\phi [A_{x^i_\xi }\setminus F_i^\xi ]\subseteq I_i$
.
As
![]() $I_i\cap I_j=\emptyset $
for distinct
$I_i\cap I_j=\emptyset $
for distinct
![]() $i, j\leq k$
condition (2) implies that
$i, j\leq k$
condition (2) implies that
-
(3)
 $(A_{x^i_\xi }\setminus F_i^\xi )\cap (A_{x^j_\eta }\setminus F_j^\eta )=\emptyset $
for any
$(A_{x^i_\xi }\setminus F_i^\xi )\cap (A_{x^j_\eta }\setminus F_j^\eta )=\emptyset $
for any
 $\xi , \eta <\kappa $
and
$\xi , \eta <\kappa $
and
 $1\leq i<j\leq k$
.
$1\leq i<j\leq k$
.
As the cofinality of
![]() $\kappa $
is uncountable and there are countably many such k-tuples of sets
$\kappa $
is uncountable and there are countably many such k-tuples of sets
![]() $(F_1^\xi , \dots F_k^\xi )$
(as they are all subsets of
$(F_1^\xi , \dots F_k^\xi )$
(as they are all subsets of
![]() $\mathbb {N}$
), we may choose
$\mathbb {N}$
), we may choose
![]() $\Gamma \subseteq \Gamma '$
of cardinality
$\Gamma \subseteq \Gamma '$
of cardinality
![]() $\kappa $
such that
$\kappa $
such that
![]() $(F_1^\xi , \dots F_k^\xi )$
is equal to some fixed
$(F_1^\xi , \dots F_k^\xi )$
is equal to some fixed
![]() $(F_1, \dots F_k)$
.
$(F_1, \dots F_k)$
.
It remains to prove the property of
![]() $\Gamma $
stated in the lemma. Fix distinct
$\Gamma $
stated in the lemma. Fix distinct
![]() $\xi , \eta \in \Gamma $
and
$\xi , \eta \in \Gamma $
and
![]() $1\leq i<j\leq k$
. Then by (1) and (3) for all
$1\leq i<j\leq k$
. Then by (1) and (3) for all
![]() $1\leq i<j\leq k$
, we have
$1\leq i<j\leq k$
, we have
By (1), this set is included in
![]() $(A_{x_i^\xi }\cap A_{x_j^\xi })\cup (A_{x_j^\eta }\cap A_{x_i^\eta })$
which is included in F by the hypothesis of the lemma. So we obtain
$(A_{x_i^\xi }\cap A_{x_j^\xi })\cup (A_{x_j^\eta }\cap A_{x_i^\eta })$
which is included in F by the hypothesis of the lemma. So we obtain
![]() $A_{x_i^\xi }\cap A_{x_j^\eta }\subseteq F$
as required.
$A_{x_i^\xi }\cap A_{x_j^\eta }\subseteq F$
as required.
Proposition 15. Suppose that
![]() $\mathcal {A}$
is an
$\mathcal {A}$
is an
![]() $\mathbb {R}$
-embeddable almost disjoint family of subsets of
$\mathbb {R}$
-embeddable almost disjoint family of subsets of
![]() $\mathbb {N}$
. Whenever
$\mathbb {N}$
. Whenever
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\mathcal {Y}$
is a subset of of the unit sphere of
$\mathcal {Y}$
is a subset of of the unit sphere of
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
of regular uncountable cardinality
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
of regular uncountable cardinality
![]() $\kappa $
, there is
$\kappa $
, there is
![]() $\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
$\mathcal {Y}'\subseteq \mathcal {Y}$
of cardinality
![]() $\kappa $
which is
$\kappa $
which is
![]() $(1+\varepsilon )$
-concentrated.
$(1+\varepsilon )$
-concentrated.
Proof. We may label elements of
![]() $\mathcal {A}$
as
$\mathcal {A}$
as
![]() $A_x$
for
$A_x$
for
![]() $x\in X$
for some
$x\in X$
for some
![]() $X\subseteq [0,1]$
.
$X\subseteq [0,1]$
.
Fix a subset
![]() $\mathcal {Y}=\{f_\xi : \xi <\kappa \}$
of the unit sphere of
$\mathcal {Y}=\{f_\xi : \xi <\kappa \}$
of the unit sphere of
![]() $(\mathcal X_{\mathcal {A}},\|\ \|_\infty )$
of uncountable regular cardinality
$(\mathcal X_{\mathcal {A}},\|\ \|_\infty )$
of uncountable regular cardinality
![]() $\kappa $
. By the definition of
$\kappa $
. By the definition of
![]() $\mathcal {X}_{\mathcal {A}}$
for each
$\mathcal {X}_{\mathcal {A}}$
for each
![]() $\xi <\kappa $
, there are finite sets
$\xi <\kappa $
, there are finite sets
![]() $\{x^\xi _1, \dots x^\xi _{m_\xi }\}\subseteq X$
(
$\{x^\xi _1, \dots x^\xi _{m_\xi }\}\subseteq X$
(
![]() $x^\xi _i\not =x^\xi _j$
for
$x^\xi _i\not =x^\xi _j$
for
![]() $1\leq i< j\leq m_\xi $
and
$1\leq i< j\leq m_\xi $
and
![]() $\xi <\kappa $
), distinct rationals
$\xi <\kappa $
), distinct rationals
![]() $q^\xi _1, \dots q^\xi _{m_\xi }$
for all
$q^\xi _1, \dots q^\xi _{m_\xi }$
for all
![]() $\xi <\kappa $
and rational valued finitely supported
$\xi <\kappa $
and rational valued finitely supported
![]() $g_\xi \in c_0$
such that
$g_\xi \in c_0$
such that
 $$ \begin{align*}\Big\|f_\xi-\big(g_\xi+\sum_{1\leq i\leq m_\xi} q^\xi_i 1_{A_{x^\xi_i}} \big)\Big\|_\infty \leq \varepsilon/3.\end{align*} $$
$$ \begin{align*}\Big\|f_\xi-\big(g_\xi+\sum_{1\leq i\leq m_\xi} q^\xi_i 1_{A_{x^\xi_i}} \big)\Big\|_\infty \leq \varepsilon/3.\end{align*} $$
Using the uncountable cofinality of
![]() $\kappa $
by passing to a subset of cardinality
$\kappa $
by passing to a subset of cardinality
![]() $\kappa $
, we may assume that for all
$\kappa $
, we may assume that for all
![]() $\xi <\omega _1$
we have
$\xi <\omega _1$
we have
![]() $m_\xi =m$
for some
$m_\xi =m$
for some
![]() $m\in \mathbb {N}$
,
$m\in \mathbb {N}$
,
![]() $g_\xi =g$
for some finitely supported
$g_\xi =g$
for some finitely supported
![]() $g\in c_0$
, and that
$g\in c_0$
, and that
![]() $q^\xi _i=q_i$
for some rationals
$q^\xi _i=q_i$
for some rationals
![]() $q_i$
for all
$q_i$
for all
![]() $1\leq i\leq m$
and for all
$1\leq i\leq m$
and for all
![]() $\xi <\kappa $
. Since for a regular cardinal
$\xi <\kappa $
. Since for a regular cardinal
![]() $\kappa $
any family of
$\kappa $
any family of
![]() $\kappa $
-many finite sets contains a subfamily of cardinality
$\kappa $
-many finite sets contains a subfamily of cardinality
![]() $\kappa $
such that the intersection of any two distinct members of the subfamily is a fixed finite
$\kappa $
such that the intersection of any two distinct members of the subfamily is a fixed finite
![]() $\Delta \subseteq \kappa $
(A version of the
$\Delta \subseteq \kappa $
(A version of the
![]() $\Delta $
-system lemma, Example 25.3 of [Reference Komjáth and Totik26]) by passing to a subset of cardinality
$\Delta $
-system lemma, Example 25.3 of [Reference Komjáth and Totik26]) by passing to a subset of cardinality
![]() $\kappa $
, we may assume that there is such a
$\kappa $
, we may assume that there is such a
![]() $\Delta $
satisfying
$\Delta $
satisfying
for every
![]() $\xi <\eta <\kappa $
. By passing to a subset of cardinality
$\xi <\eta <\kappa $
. By passing to a subset of cardinality
![]() $\kappa $
, we may assume that there is a fixed
$\kappa $
, we may assume that there is a fixed
![]() $G\subseteq \{1, \dots , m\}$
such that
$G\subseteq \{1, \dots , m\}$
such that
![]() $\Delta =\{x^\xi _i: i\in G\}$
for every
$\Delta =\{x^\xi _i: i\in G\}$
for every
![]() $\xi <\kappa $
. If
$\xi <\kappa $
. If
![]() $G=\{1, \dots , m\}$
, we conclude that
$G=\{1, \dots , m\}$
, we conclude that
![]() $\{f_\xi : \xi <\kappa \}$
is even
$\{f_\xi : \xi <\kappa \}$
is even
![]() $2\varepsilon /3$
-concentrated, so we will assume that G is a proper subset of
$2\varepsilon /3$
-concentrated, so we will assume that G is a proper subset of
![]() $\{1, \dots , m\}$
. So by reordering
$\{1, \dots , m\}$
. So by reordering
![]() $\{1, \dots , m\}$
, we may assume that there is
$\{1, \dots , m\}$
, we may assume that there is
![]() $1\leq k\leq m$
such that the sets
$1\leq k\leq m$
such that the sets
![]() $\{x^\xi _1, \dots x^\xi _{k}\}$
are pairwise disjoint for
$\{x^\xi _1, \dots x^\xi _{k}\}$
are pairwise disjoint for
![]() $\xi <\kappa $
and
$\xi <\kappa $
and
![]() $\{x^\xi _{k+1}, \dots x^\xi _{m}\}=\{x_{k+1}, \dots x_m\}=\Delta $
for some
$\{x^\xi _{k+1}, \dots x^\xi _{m}\}=\{x_{k+1}, \dots x_m\}=\Delta $
for some
![]() $x_{k+1}, \dots x_m\in X$
for each
$x_{k+1}, \dots x_m\in X$
for each
![]() $\xi <\kappa $
. So for every
$\xi <\kappa $
. So for every
![]() $\xi <\kappa $
, we have
$\xi <\kappa $
, we have
 $$ \begin{align}\Big\|f_\xi-\big(g+\sum_{1\leq i\leq m} q_i 1_{A_{x^\xi_i}} \big)\Big\|_\infty\leq \varepsilon/3.\end{align} $$
$$ \begin{align}\Big\|f_\xi-\big(g+\sum_{1\leq i\leq m} q_i 1_{A_{x^\xi_i}} \big)\Big\|_\infty\leq \varepsilon/3.\end{align} $$
And for every
![]() $\xi <\eta <\kappa $
, we have
$\xi <\eta <\kappa $
, we have
Also, as for each
![]() $1\leq j\leq k$
, we have
$1\leq j\leq k$
, we have
![]() $\lim _{n\in A_{x^\xi _j}}|f_\xi (n)|\leq 1$
since the elements
$\lim _{n\in A_{x^\xi _j}}|f_\xi (n)|\leq 1$
since the elements
![]() $f_\xi $
are taken from the unit sphere in the
$f_\xi $
are taken from the unit sphere in the
![]() $\|\ \|_\infty $
-norm, and
$\|\ \|_\infty $
-norm, and
![]() $\lim _{n\in A_{x^\xi _j}}g(n)=0$
as
$\lim _{n\in A_{x^\xi _j}}g(n)=0$
as
![]() $g\in c_0$
and
$g\in c_0$
and
 $$ \begin{align*}\lim_{n\in A_{x^\xi_j}}\Big(\sum_{1\leq i\leq m} q_i 1_{A_{x^\xi_i}}\Big)(n)=q_j,\end{align*} $$
$$ \begin{align*}\lim_{n\in A_{x^\xi_j}}\Big(\sum_{1\leq i\leq m} q_i 1_{A_{x^\xi_i}}\Big)(n)=q_j,\end{align*} $$
by Lemma 5, so we may conclude from (1) that for all
![]() $1\leq j\leq k$
we have
$1\leq j\leq k$
we have
Moreover, since there are countably many finite subsets of
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\kappa $
is of uncountable cofinality, we may assume that there is a fixed finite
$\kappa $
is of uncountable cofinality, we may assume that there is a fixed finite
![]() $F\subseteq \mathbb {N}$
such that
$F\subseteq \mathbb {N}$
such that
Using Lemma 14 and the hypothesis that
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\mathbb {R}$
-embeddable, there is subset
$\mathbb {R}$
-embeddable, there is subset
![]() $\Gamma \subseteq \kappa $
of cardinality
$\Gamma \subseteq \kappa $
of cardinality
![]() $\kappa $
such that
$\kappa $
such that
Since there are countably many rational valued functions defined on F, by passing to a subset of
![]() $\Gamma $
of cardinality
$\Gamma $
of cardinality
![]() $\kappa $
we may also assume that for each
$\kappa $
we may also assume that for each
![]() $\xi , \eta \in \Gamma $
and each
$\xi , \eta \in \Gamma $
and each
![]() $n\in F$
we have
$n\in F$
we have
So by (5), the following are the only possible cases for
![]() $n\in \mathbb {N}$
:
$n\in \mathbb {N}$
:
 $$ \begin{align*}\Big(\sum_{1\leq i\leq k} q_i 1_{A_{x^\xi_i}}-\sum_{1\leq i\leq k} q_i 1_{A_{x^\eta_i}}\Big)(n) = \begin{cases} 0 & \text{if }n\in F, \\ q_i-q_i=0 & \text{if }n\in A_{x^\xi_i}\cap A_{x^\eta_i}\setminus F\text{ for some }i,\\ q_i& \text{if }n\in A_{x^\xi_i}\setminus (A_{x^\eta_i}\cup F)\text{ for some }i,\\ -q_i& \text{if }\in A_{x^\eta_i}\setminus (A_{x^\xi_i}\cup F)\text{ for some }i,\\ 0& \text{if }n\not\in \bigcup_{1\leq i\leq k}(A_{x^\xi_i}\cup A_{x^\eta_i}). \end{cases} \end{align*} $$
$$ \begin{align*}\Big(\sum_{1\leq i\leq k} q_i 1_{A_{x^\xi_i}}-\sum_{1\leq i\leq k} q_i 1_{A_{x^\eta_i}}\Big)(n) = \begin{cases} 0 & \text{if }n\in F, \\ q_i-q_i=0 & \text{if }n\in A_{x^\xi_i}\cap A_{x^\eta_i}\setminus F\text{ for some }i,\\ q_i& \text{if }n\in A_{x^\xi_i}\setminus (A_{x^\eta_i}\cup F)\text{ for some }i,\\ -q_i& \text{if }\in A_{x^\eta_i}\setminus (A_{x^\xi_i}\cup F)\text{ for some }i,\\ 0& \text{if }n\not\in \bigcup_{1\leq i\leq k}(A_{x^\xi_i}\cup A_{x^\eta_i}). \end{cases} \end{align*} $$
By (3), it follows that
 $$ \begin{align*}\Big\|\sum_{1\leq i\leq k} q_i 1_{A_{x^\xi_i}}-\sum_{1\leq i\leq k} q_i 1_{A_{x^\eta_i}}\Big\|_\infty\leq \max\{|q_i|: 1\leq i\leq k\}\leq 1+\varepsilon/3\end{align*} $$
$$ \begin{align*}\Big\|\sum_{1\leq i\leq k} q_i 1_{A_{x^\xi_i}}-\sum_{1\leq i\leq k} q_i 1_{A_{x^\eta_i}}\Big\|_\infty\leq \max\{|q_i|: 1\leq i\leq k\}\leq 1+\varepsilon/3\end{align*} $$
which by (2) implies the required
![]() $\|f_\xi -f_\eta \|\leq 1+\varepsilon $
for any
$\|f_\xi -f_\eta \|\leq 1+\varepsilon $
for any
![]() $\xi , \eta \in \Gamma $
.
$\xi , \eta \in \Gamma $
.
Remark 16. We note that in the language of the paper [Reference Hrušák and Guzmán20] of Hrušák and Guzmán an almost disjoint family
![]() $\mathcal {A}$
cannot have both the property from Lemma 14 and contain an n-Luzin gap for some
$\mathcal {A}$
cannot have both the property from Lemma 14 and contain an n-Luzin gap for some
![]() $n\in \mathbb {N}$
. They showed that under the assumption of MA and the negation of CH every almost disjoint family of cardinality smaller than continuum which contains no n-Luzin gaps for any
$n\in \mathbb {N}$
. They showed that under the assumption of MA and the negation of CH every almost disjoint family of cardinality smaller than continuum which contains no n-Luzin gaps for any
![]() $n\in \mathbb {N}$
is
$n\in \mathbb {N}$
is
![]() $\mathbb {R}$
-embeddable.
$\mathbb {R}$
-embeddable.
Remark 17. By Proposition 15, for every
![]() $\varepsilon>0$
the space
$\varepsilon>0$
the space
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
for an
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
for an
![]() $\mathbb {R}$
-embeddable almost disjoint family
$\mathbb {R}$
-embeddable almost disjoint family
![]() $\mathcal {A}$
admits no uncountable
$\mathcal {A}$
admits no uncountable
![]() $(1+\varepsilon )$
-separated set in its unit sphere. Nevertheless, such spaces always admit
$(1+\varepsilon )$
-separated set in its unit sphere. Nevertheless, such spaces always admit
![]() $(1+)$
-separated sets of unit vectors of the cardinality equal to the density of
$(1+)$
-separated sets of unit vectors of the cardinality equal to the density of
![]() $\mathcal {X}_{\mathcal {A}}$
. For
$\mathcal {X}_{\mathcal {A}}$
. For
![]() $A\in \mathcal {A}$
, define
$A\in \mathcal {A}$
, define
Then given any two distinct
![]() $A, A'\in \mathcal {A}$
, choose
$A, A'\in \mathcal {A}$
, choose
![]() $k\in A\setminus A'$
and observe that we have
$k\in A\setminus A'$
and observe that we have
![]() $\|f_A-f_{A'}\|\geq |f_A-f_{A'}|(k)=1-(-1/({k+1}))>1$
.
$\|f_A-f_{A'}\|\geq |f_A-f_{A'}|(k)=1-(-1/({k+1}))>1$
.
4 Separation in spheres of Banach spaces
 $(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
induced by Luzin almost disjoint families
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
induced by Luzin almost disjoint families
Definition 18. An almost disjoint family
![]() $\{A_\xi : \xi <\omega _1\}$
is called a Luzin family if
$\{A_\xi : \xi <\omega _1\}$
is called a Luzin family if
![]() $f_\alpha : \alpha \rightarrow \mathbb {N}$
is finite-to-one for any
$f_\alpha : \alpha \rightarrow \mathbb {N}$
is finite-to-one for any
![]() $\alpha <\omega _1$
, where
$\alpha <\omega _1$
, where
for every
![]() $\beta <\alpha <\omega _1$
.
$\beta <\alpha <\omega _1$
.
Lemma 19 [Reference Luzin33]
Luzin families exist.
Luzin families were first constructed in [Reference Luzin33]. See Section 3.1. of [Reference Hrušák21] for the construction and for more information.
Proposition 20. Suppose that
![]() $\mathcal L=\{A_\xi : \xi <\omega _1\}$
is a Luzin family, and
$\mathcal L=\{A_\xi : \xi <\omega _1\}$
is a Luzin family, and
![]() $\xi _\alpha , \eta _\alpha $
satisfy
$\xi _\alpha , \eta _\alpha $
satisfy
for all
![]() $\beta <\alpha <\omega _1$
. Then
$\beta <\alpha <\omega _1$
. Then
![]() $(\mathcal {X}_{\mathcal L}, \|\ \|_\infty )$
admits an uncountable
$(\mathcal {X}_{\mathcal L}, \|\ \|_\infty )$
admits an uncountable
![]() $2$
-equilateral set
$2$
-equilateral set
![]() $\{f_\alpha : \alpha \in X\}$
among elements of its unit sphere of the form
$\{f_\alpha : \alpha \in X\}$
among elements of its unit sphere of the form
for all
![]() $\alpha \in \Gamma $
for some uncountable
$\alpha \in \Gamma $
for some uncountable
![]() $\Gamma \subseteq \omega _1$
.
$\Gamma \subseteq \omega _1$
.
Proof. It is clear that
![]() $\|f_\alpha \|_\infty \leq 1$
for each
$\|f_\alpha \|_\infty \leq 1$
for each
![]() $\alpha <\omega _1$
as
$\alpha <\omega _1$
as
![]() $f_\alpha $
may assume values among
$f_\alpha $
may assume values among
![]() $\{-1,0, 1\}$
. Since
$\{-1,0, 1\}$
. Since
![]() $A_{\xi _\alpha }\cap A_{\eta _\alpha }$
is finite and both
$A_{\xi _\alpha }\cap A_{\eta _\alpha }$
is finite and both
![]() $A_{\xi _\alpha }, A_{\eta _\alpha }$
are infinite, we have that
$A_{\xi _\alpha }, A_{\eta _\alpha }$
are infinite, we have that
![]() $\|f_\alpha \|=1$
for each
$\|f_\alpha \|=1$
for each
![]() $\alpha <\omega _1$
. Let
$\alpha <\omega _1$
. Let
![]() $F_\alpha \subseteq \mathbb {N}$
for
$F_\alpha \subseteq \mathbb {N}$
for
![]() $\alpha <\omega _1$
be such a finite set that
$\alpha <\omega _1$
be such a finite set that
![]() $A_{\xi _\alpha }\cap A_{\eta _\alpha }\subseteq F_\alpha $
. By passing to an uncountable subset, we may assume that
$A_{\xi _\alpha }\cap A_{\eta _\alpha }\subseteq F_\alpha $
. By passing to an uncountable subset, we may assume that
![]() $F_\alpha =F$
for each
$F_\alpha =F$
for each
![]() $\alpha <\omega _1$
and some finite
$\alpha <\omega _1$
and some finite
![]() $F\subseteq \mathbb {N}$
. Let
$F\subseteq \mathbb {N}$
. Let
![]() $k\in \mathbb {N}$
be such that
$k\in \mathbb {N}$
be such that
![]() $F\subseteq \{1, \dots , k\}$
. Now, we will use the following version of Erdös-Dushnik-Miller theorem: Whenever
$F\subseteq \{1, \dots , k\}$
. Now, we will use the following version of Erdös-Dushnik-Miller theorem: Whenever
![]() $\kappa $
is regular and uncountable cardinal and
$\kappa $
is regular and uncountable cardinal and
![]() $c:[\kappa ]^2\rightarrow \{0,1\}$
, then either there is
$c:[\kappa ]^2\rightarrow \{0,1\}$
, then either there is
![]() $1$
-monochromatic set of cardinality
$1$
-monochromatic set of cardinality
![]() $\kappa $
or there is a
$\kappa $
or there is a
![]() $0$
-monochromatic set of order type
$0$
-monochromatic set of order type
![]() $\omega +1$
(see 24.32 of [Reference Komjáth and Totik26]). Consider a coloring
$\omega +1$
(see 24.32 of [Reference Komjáth and Totik26]). Consider a coloring
![]() $c:[\omega _1]^{2}\rightarrow \{0,1\}$
defined by
$c:[\omega _1]^{2}\rightarrow \{0,1\}$
defined by
![]() $c(\{\beta , \alpha \})=0$
if
$c(\{\beta , \alpha \})=0$
if
![]() $f_{\xi _\alpha }(\eta _\beta )\leq k$
for the ordering of the elements
$f_{\xi _\alpha }(\eta _\beta )\leq k$
for the ordering of the elements
![]() $\beta <\alpha $
and
$\beta <\alpha $
and
![]() $c(\{\beta , \alpha \})=1$
otherwise. Note that there cannot be a
$c(\{\beta , \alpha \})=1$
otherwise. Note that there cannot be a
![]() $0$
-monochromatic set
$0$
-monochromatic set
![]() $\Delta \subseteq \omega _1$
of order type
$\Delta \subseteq \omega _1$
of order type
![]() $\omega +1$
because denoting its biggest element as
$\omega +1$
because denoting its biggest element as
![]() $\alpha $
we would have that
$\alpha $
we would have that
![]() $f_{\xi _\alpha }|\{\eta _\beta : \beta \in \Delta \cap \alpha \}$
is bounded below by k which would contradict the hypothesis that
$f_{\xi _\alpha }|\{\eta _\beta : \beta \in \Delta \cap \alpha \}$
is bounded below by k which would contradict the hypothesis that
![]() $\mathcal L$
is a Luzin family, that is, that the functions
$\mathcal L$
is a Luzin family, that is, that the functions
![]() $f_{\xi _\alpha }$
are finite-to-one. So it follows that there is an uncountable
$f_{\xi _\alpha }$
are finite-to-one. So it follows that there is an uncountable
![]() $1$
-monochromatic
$1$
-monochromatic
![]() $\Gamma \subseteq \omega _1$
for the coloring c.
$\Gamma \subseteq \omega _1$
for the coloring c.
For
![]() $\alpha , \beta \in \Gamma $
with
$\alpha , \beta \in \Gamma $
with
![]() $\beta <\alpha $
, there is
$\beta <\alpha $
, there is
![]() $m>k$
such that
$m>k$
such that
![]() $m\in A_{\xi _\alpha }\cap A_{\eta _\beta }$
. By the choice of F and the fact that
$m\in A_{\xi _\alpha }\cap A_{\eta _\beta }$
. By the choice of F and the fact that
![]() $F\subseteq \{1, \dots , k\}$
, we have that neither
$F\subseteq \{1, \dots , k\}$
, we have that neither
![]() $m\in A_{\eta _\alpha }$
nor
$m\in A_{\eta _\alpha }$
nor
![]() $m\in A_{\xi _\beta }$
, and so it follows that
$m\in A_{\xi _\beta }$
, and so it follows that
Proposition 21. Suppose that
![]() $\mathcal L=\{A_\xi : \xi <\omega _1\}$
is a Luzin family,
$\mathcal L=\{A_\xi : \xi <\omega _1\}$
is a Luzin family,
![]() $\mathcal {A}$
is an almost disjoint family such that
$\mathcal {A}$
is an almost disjoint family such that
![]() $\mathcal L\subseteq \mathcal {A}$
,
$\mathcal L\subseteq \mathcal {A}$
,
![]() $\mathcal {X}$
is a Banach space and
$\mathcal {X}$
is a Banach space and
![]() $T:\mathcal X_{\mathcal {A}}\rightarrow \mathcal {X}$
is a bounded linear operator with separable range. Then for every
$T:\mathcal X_{\mathcal {A}}\rightarrow \mathcal {X}$
is a bounded linear operator with separable range. Then for every
![]() $\varepsilon \in (0,1)$
the unit sphere of
$\varepsilon \in (0,1)$
the unit sphere of
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
admits an uncountable
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
admits an uncountable
![]() $(2-\varepsilon )$
-separated set.
$(2-\varepsilon )$
-separated set.
Proof. As
![]() $\mathcal {X}_{\mathcal L}$
is a subspace of
$\mathcal {X}_{\mathcal L}$
is a subspace of
![]() $\mathcal {X}_{\mathcal {A}}$
, we can assume that
$\mathcal {X}_{\mathcal {A}}$
, we can assume that
![]() $\mathcal {A}=\mathcal L$
. By Lemma 8, there is an uncountable subset
$\mathcal {A}=\mathcal L$
. By Lemma 8, there is an uncountable subset
![]() $\Xi \subseteq \omega _1$
such that
$\Xi \subseteq \omega _1$
such that
 $$ \begin{align}\|T(1_{A_\xi}-1_{A_\eta})\|\leq {\varepsilon/2\over{1-\varepsilon/2}}\end{align} $$
$$ \begin{align}\|T(1_{A_\xi}-1_{A_\eta})\|\leq {\varepsilon/2\over{1-\varepsilon/2}}\end{align} $$
for every
![]() $\xi , \eta \in \Xi $
. Let
$\xi , \eta \in \Xi $
. Let
![]() $\{\xi _\alpha : \alpha <\omega _1\}$
and
$\{\xi _\alpha : \alpha <\omega _1\}$
and
![]() $(\eta _\alpha : \alpha <\omega _1)$
be enumerations of two uncountable and disjoint subsets of
$(\eta _\alpha : \alpha <\omega _1)$
be enumerations of two uncountable and disjoint subsets of
![]() $\Xi $
satisfying for all
$\Xi $
satisfying for all
![]() $\beta <\alpha <\omega _1$
the following conditions
$\beta <\alpha <\omega _1$
the following conditions
By Proposition 20, there is an uncountable
![]() $\Gamma \subseteq \omega _1$
such that
$\Gamma \subseteq \omega _1$
such that
![]() $\{f_\alpha : \alpha \in \Gamma \}$
is a
$\{f_\alpha : \alpha \in \Gamma \}$
is a
![]() $2$
-equilateral set of the unit sphere of
$2$
-equilateral set of the unit sphere of
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
, where for each
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_\infty )$
, where for each
![]() $\alpha \in \Gamma $
we have
$\alpha \in \Gamma $
we have
For
![]() $\alpha \in \Gamma $
, consider
$\alpha \in \Gamma $
, consider
We claim that
![]() $\{g_\alpha : \alpha \in \Gamma \}$
is the desired
$\{g_\alpha : \alpha \in \Gamma \}$
is the desired
![]() $(2-\varepsilon )$
-separated set of the unit sphere of
$(2-\varepsilon )$
-separated set of the unit sphere of
![]() $(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
. To prove it take
$(\mathcal {X}_{\mathcal {A}}, \|\ \|_T)$
. To prove it take
![]() $\beta <\alpha $
with
$\beta <\alpha $
with
![]() $\alpha , \beta \in \Gamma $
. As
$\alpha , \beta \in \Gamma $
. As
it is enough to prove that
![]() $\|g_\alpha -g_\beta \|_{\infty }\geq 2-\varepsilon $
. We have
$\|g_\alpha -g_\beta \|_{\infty }\geq 2-\varepsilon $
. We have
 $$ \begin{align*}\|g_\alpha-g_\beta\|_{\infty}= \|{{f_\alpha}\over{\|f_\alpha\|_T}}-{{f_\alpha}\over{\|f_\alpha\|_T}}\|_\infty \geq \|f_\alpha-f_\beta\|_\infty-\|{{f_\alpha}\over{\|f_\alpha\|_T}}-f_\alpha\|_\infty -\|{{f_\beta}\over{\|f_\beta\|_T}}-f_\beta\|_\infty.\end{align*} $$
$$ \begin{align*}\|g_\alpha-g_\beta\|_{\infty}= \|{{f_\alpha}\over{\|f_\alpha\|_T}}-{{f_\alpha}\over{\|f_\alpha\|_T}}\|_\infty \geq \|f_\alpha-f_\beta\|_\infty-\|{{f_\alpha}\over{\|f_\alpha\|_T}}-f_\alpha\|_\infty -\|{{f_\beta}\over{\|f_\beta\|_T}}-f_\beta\|_\infty.\end{align*} $$
Since
![]() $\alpha , \beta \in \Gamma $
, we have
$\alpha , \beta \in \Gamma $
, we have
![]() $\|f_\alpha \|_\infty =\|f_\beta \|_\infty =1$
,
$\|f_\alpha \|_\infty =\|f_\beta \|_\infty =1$
,
![]() $\|f_\alpha -f_\beta \|_\infty =2$
. So now, we estimate
$\|f_\alpha -f_\beta \|_\infty =2$
. So now, we estimate
 $$ \begin{align*}\|{{f_\alpha}\over{\|f_\alpha\|_T}}-f_\alpha\|_\infty= \Big| {1\over{\|f_\alpha\|_\infty+\|T(f_\alpha)\|_{\mathcal{X}}}} -1\Big|\|f_\alpha\|_\infty=\Big| {1\over{1+\|T(f_\alpha)\|_{\mathcal{X}}}} -1\Big|. \end{align*} $$
$$ \begin{align*}\|{{f_\alpha}\over{\|f_\alpha\|_T}}-f_\alpha\|_\infty= \Big| {1\over{\|f_\alpha\|_\infty+\|T(f_\alpha)\|_{\mathcal{X}}}} -1\Big|\|f_\alpha\|_\infty=\Big| {1\over{1+\|T(f_\alpha)\|_{\mathcal{X}}}} -1\Big|. \end{align*} $$
By equation (*), we have
![]() $\|T(f_\alpha )\|_{\mathcal {X}}\leq {\varepsilon /2\over {1-\varepsilon /2}}$
, and so
$\|T(f_\alpha )\|_{\mathcal {X}}\leq {\varepsilon /2\over {1-\varepsilon /2}}$
, and so
 $$ \begin{align*}1-\varepsilon/2= {1\over{1+{\varepsilon/2\over{1-\varepsilon/2}}}}\leq {1\over{1+\|T(f_\alpha)\|_{\mathcal{X}}}} \leq 1,\end{align*} $$
$$ \begin{align*}1-\varepsilon/2= {1\over{1+{\varepsilon/2\over{1-\varepsilon/2}}}}\leq {1\over{1+\|T(f_\alpha)\|_{\mathcal{X}}}} \leq 1,\end{align*} $$
and so
 $$ \begin{align*}\|{{f_\alpha}\over{\|f_\alpha\|_T}}-f_\alpha\|_\infty\leq \varepsilon/2.\end{align*} $$
$$ \begin{align*}\|{{f_\alpha}\over{\|f_\alpha\|_T}}-f_\alpha\|_\infty\leq \varepsilon/2.\end{align*} $$
The same calculation works for
![]() $\|{{f_\beta }\over {\|f_\beta \|_T}}-f_\beta \|_\infty ,$
so we conclude that
$\|{{f_\beta }\over {\|f_\beta \|_T}}-f_\beta \|_\infty ,$
so we conclude that
as required.
5 Final remarks and open problems
Recall that the Ramsey theorem says that given any
![]() $k\in \mathbb {N}$
and any coloring
$k\in \mathbb {N}$
and any coloring
![]() $c: [\mathbb {N}]^2\rightarrow \{1, \dots , k\}$
there is an infinite
$c: [\mathbb {N}]^2\rightarrow \{1, \dots , k\}$
there is an infinite
![]() $A\subseteq \mathbb {N}$
which is i-monochromatic for c for some
$A\subseteq \mathbb {N}$
which is i-monochromatic for c for some
![]() $1\leq i\leq k$
, that is,
$1\leq i\leq k$
, that is,
![]() $c[[A]^2]=\{i\}$
. On the other hand, colorings of all pairs of uncountable cardinals not bigger than continuum may not have uncountable monochromatic sets as already shown by Sierpiński (24.23 of [Reference Komjáth and Totik26]). The phenomena considered in this paper can be seen from a Ramsey theoretic point of view. For example, given a Banach space X one can consider a coloring
$c[[A]^2]=\{i\}$
. On the other hand, colorings of all pairs of uncountable cardinals not bigger than continuum may not have uncountable monochromatic sets as already shown by Sierpiński (24.23 of [Reference Komjáth and Totik26]). The phenomena considered in this paper can be seen from a Ramsey theoretic point of view. For example, given a Banach space X one can consider a coloring
![]() $c:[S_{\mathcal {X}}]^2\rightarrow \{-1,0,1\}$
given by
$c:[S_{\mathcal {X}}]^2\rightarrow \{-1,0,1\}$
given by
 $$ \begin{align*}c_{\mathcal{X}}(x, y)= \begin{cases} -1 & \text{if }\|x-y\|<1 \\ 0 & \text{if }\|x-y\|=1 \\ 1 & \text{if }\|x-y\|>1. \end{cases} \end{align*} $$
$$ \begin{align*}c_{\mathcal{X}}(x, y)= \begin{cases} -1 & \text{if }\|x-y\|<1 \\ 0 & \text{if }\|x-y\|=1 \\ 1 & \text{if }\|x-y\|>1. \end{cases} \end{align*} $$
A
![]() $(1+)$
-separated set in
$(1+)$
-separated set in
![]() $S_{\mathcal {X}}$
is a
$S_{\mathcal {X}}$
is a
![]() $1$
-monochromatic set for
$1$
-monochromatic set for
![]() $c_{\mathcal {X}}$
, and by an observation of Terenzi mentioned in the introduction, the existence of an uncountable equilateral set in
$c_{\mathcal {X}}$
, and by an observation of Terenzi mentioned in the introduction, the existence of an uncountable equilateral set in
![]() $\mathcal {X}$
is equivalent to the existence of an uncountable
$\mathcal {X}$
is equivalent to the existence of an uncountable
![]() $0$
-monochromatic set for
$0$
-monochromatic set for
![]() $c_{\mathcal {X}}$
. On the other hand, our main result says that there is a nonseparable Banach space
$c_{\mathcal {X}}$
. On the other hand, our main result says that there is a nonseparable Banach space
![]() $\mathcal {X}$
such that every uncountable subset of
$\mathcal {X}$
such that every uncountable subset of
![]() $S_{\mathcal {X}}$
contains an uncountable (
$S_{\mathcal {X}}$
contains an uncountable (
![]() $-1$
)-monochromatic set. It is not accidental that the separable results of Kottman or Elton and Odell employ the Ramsey theorem [Reference Kottman30, Reference Elton and Odell9]. However, we are still far from understanding the structure of monochomatic sets for the colorings
$-1$
)-monochromatic set. It is not accidental that the separable results of Kottman or Elton and Odell employ the Ramsey theorem [Reference Kottman30, Reference Elton and Odell9]. However, we are still far from understanding the structure of monochomatic sets for the colorings
![]() $c_{\mathcal {X}}$
. For example, it is natural to ask if the following dichotomy holds:
$c_{\mathcal {X}}$
. For example, it is natural to ask if the following dichotomy holds:
Question 22. Is it true that the unit sphere of every nonseparable Banach space
![]() $\mathcal {X}$
either contains a
$\mathcal {X}$
either contains a
![]() $(1+)$
-separated set or every uncountable subset of the sphere
$(1+)$
-separated set or every uncountable subset of the sphere
![]() $S_{\mathcal {X}}$
contains an uncountable subset which is
$S_{\mathcal {X}}$
contains an uncountable subset which is
![]() $(1-)$
-concentrated (or
$(1-)$
-concentrated (or
![]() $(1-\varepsilon )$
-concentrated for some
$(1-\varepsilon )$
-concentrated for some
![]() $\varepsilon>0$
)?
$\varepsilon>0$
)?
Here, by
![]() $(1-)$
-concentrated we mean a set
$(1-)$
-concentrated we mean a set
![]() $\mathcal {Y}\subseteq \mathcal {X}$
such that
$\mathcal {Y}\subseteq \mathcal {X}$
such that
![]() $\|x-y\|<1$
for any two distinct
$\|x-y\|<1$
for any two distinct
![]() $x, y\in \mathcal {Y}$
. In fact, if the above dichotomy does not hold, it would be interesting to search for a nonseparable Banach space
$x, y\in \mathcal {Y}$
. In fact, if the above dichotomy does not hold, it would be interesting to search for a nonseparable Banach space
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
![]() $c_{\mathcal {X}}$
has no uncountable
$c_{\mathcal {X}}$
has no uncountable
![]() $1$
-monochromatic sets and the family of all uncountable
$1$
-monochromatic sets and the family of all uncountable
![]() $(-1)$
-monochromatic sets is minimal in some sense. Another aspect of our paper is the following general question:
$(-1)$
-monochromatic sets is minimal in some sense. Another aspect of our paper is the following general question:
Question 23. What nonseparable metric spaces can be isometrically embedded in every nonseparable Banach space?
The Riesz lemma implies that for every
![]() $\varepsilon>0$
every nonseparable Banach space of density
$\varepsilon>0$
every nonseparable Banach space of density
![]() $\kappa $
contains a metric space
$\kappa $
contains a metric space
![]() $(M, d)$
, where
$(M, d)$
, where
![]() $M=\{0\}\cup \{x_\xi : \xi <\kappa \}$
, and where
$M=\{0\}\cup \{x_\xi : \xi <\kappa \}$
, and where
![]() $d(0, x_\xi )=1$
for all
$d(0, x_\xi )=1$
for all
![]() $\xi <\kappa $
and
$\xi <\kappa $
and
![]() $d(x_\xi , x_\eta )>1-\varepsilon $
for any
$d(x_\xi , x_\eta )>1-\varepsilon $
for any
![]() $\xi <\eta <\kappa $
. In this article, among other results, we have shown in ZFC that uncountable metric spaces, where distances between any two distinct points are the same, do not embed isometrically into all nonseparable Banach spaces. The above question has been considered on the countable level in [Reference Mercourakis and Vassiliadis39]. On the finite level, for example, Shkarin has proved in [Reference Shkarin46] that every finite ultrametric space (a metric space where the distance d satisfies
$\xi <\eta <\kappa $
. In this article, among other results, we have shown in ZFC that uncountable metric spaces, where distances between any two distinct points are the same, do not embed isometrically into all nonseparable Banach spaces. The above question has been considered on the countable level in [Reference Mercourakis and Vassiliadis39]. On the finite level, for example, Shkarin has proved in [Reference Shkarin46] that every finite ultrametric space (a metric space where the distance d satisfies
![]() $d(x, z)\leq \max (d(x, y), d(y, z))$
for any points
$d(x, z)\leq \max (d(x, y), d(y, z))$
for any points
![]() $x, y, z$
) isometrically embeds in any infinite-dimensional Banach space.
$x, y, z$
) isometrically embeds in any infinite-dimensional Banach space.
Acknowledgements
The author was partially supported by the NCN (National Science Centre, Poland) research grant no. 2020/37/B/ST1/02613. The author would like to thank H.M. Wark for comments on a preliminary version of this paper which allowed the subsequent versions to be improved.
Competing Interests
None.