Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-28T03:37:48.688Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC CLASSES IN MIXED CHARACTERISTIC AND ANDRÉ’S p-ADIC PERIODS

Published online by Cambridge University Press:  27 January 2025

Giuseppe Ancona Open the ORCID record for Giuseppe Ancona [Opens in a new window]  and
Dragoş Frăţilă
Giuseppe Ancona*
Affiliation:
IRMA, Strasbourg, France
Dragoş Frăţilă
Affiliation:
IRMA, Strasbourg, France ([email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the study of algebraic classes in mixed characteristic, we define a countable subalgebra of 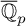${\overline {\mathbb {Q}}}_p$ which we call the algebra of André’s p-adic periods. The classical Tannakian formalism cannot be used to study these new periods. Instead, inspired by ideas of Drinfel’d on the Plücker embedding and further developed by Haines, we produce an adapted Tannakian setting which allows us to bound the transcendence degree of André’s p-adic periods and to formulate the p-adic analog of the Grothendieck period conjecture. We exhibit several examples where special values of classical p-adic functions appear as André’s p-adic periods, and we relate these new conjectures to some classical problems on algebraic classes.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , First View , pp. 1 - 46
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ancona, G., ‘Standard conjectures for abelian fourfolds’, Invent. Math. 223(1) (2021), 149–212.CrossRefGoogle Scholar
André, Y., ‘ $p$ -adic Betti lattices’, in $p$ -adic Analysis (Trento, 1989), LNM, vol. 1454 (Springer, Berlin, 1990), 23–63.Google Scholar
André, Y., ‘Théorie des motifs et interprétation géométrique des valeurs $p$ -adiques de $G$ -functions (une introduction)’, in Number Theory (Paris, 1992–1993), London Math. Soc. Lecture Note Ser., vol. 215 (Cambridge Univ. Press, Cambridge, 1995), 37–60.CrossRefGoogle Scholar
André, Y., ‘Period mappings and differential equations. From $\mathbb{C}$ to ${\mathbb{C}}_p$ ’, in Tôhoku-Hokkaidô Lectures in Arithmetic Geometry, vol. 12 (2003).Google Scholar
André, Y., Une introduction aux motifs (motifs purs, motifs mixtes, périodes), Panoramas et Synthèses, vol. 17 (Société Mathématique de France, Paris, 2004).Google Scholar
André, Y., ‘On the observability of Galois representations and the Tate conjecture,’ Journal of Number Theory, 2024. To appear.Google Scholar
Ayoub, J., ‘Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. I’, Astérisque, (314) (2008).Google Scholar
Ayoub, J., ‘Une version relative de la conjecture des périodes de Kontsevich–Zagier’, Ann. of Math. (2) 181(3) (2015), 905–992.CrossRefGoogle Scholar
Ayoub, J., ‘Nouvelles cohomologies de Weil en caractéristique positive’, Algebra Number Theory 14(7) (2020), 1747–1790, 2020.CrossRefGoogle Scholar
Beauville, A., ‘Some surfaces with maximal Picard number’, Journal de l’École polytechnique—Mathématiques 1 (2014), 101–116.CrossRefGoogle Scholar
Berthelot, P., Cohomologie cristalline des schémas de caractéristique $p>0$ , LNM, vol. 407 (Springer-Verlag, Berlin-New York, 1974).0$+,+LNM,+vol.+407+(Springer-Verlag,+Berlin-New+York,+1974).>Google Scholar
Bertrand, D., ‘Sous-groupes à un paramètre $p$ -adique de variétés de groupe’, Invent. Math. 40(2) (1977), 171–193.CrossRefGoogle Scholar
Berthelot, P. and Ogus, A., ‘F-isocrystals and De Rham cohomology. I’, Invent. Math. 72 (1983), 159–199.CrossRefGoogle Scholar
Brown, F., ‘Mixed Tate motives over $\mathbb{Z}$ ’, Ann. of Math. (2) 175(2) (2012), 949–976.CrossRefGoogle Scholar
Brown, F., ‘Notes on motivic periods’, Commun. Number Theory Phys. 11(3) (2017), 557–655.CrossRefGoogle Scholar
Cisinski, D.-C. and Déglise, F., Triangulated Categories of Mixed Motives, Springer Monographs in Mathematics (Springer, Cham, 2019).CrossRefGoogle Scholar
Charles, F., ‘The Tate conjecture for $K3$ surfaces over finite fields’, Invent. Math. 194(1) (2013), 119–145.CrossRefGoogle Scholar
Coleman, R. F., ‘On the Frobenius matrices of Fermat curves’, in $p$ -adic Analysis (Trento, 1989), Lecture Notes in Math., vol. 1454 (Springer, Berlin, 1990), 173–193.Google Scholar
Curtis, C. W. and Reiner, I., ‘Methods of representation theory, with applications to finite groups and orders’, in Pure and Applied Mathematics, vol. 1. (John Wiley & Sons, New York, 1981).Google Scholar
D’Addezio, M., “Parabolicity conjecture of F-isocrystals’, Ann. of Math. 198 (2023), 619–656.Google Scholar
Deligne, P., ‘Valeurs de fonctions $L$ et périodes d’intégrales’, in Automorphic Forms, Representations and $L$ -functions, Proc. Sympos. Pure Math., part 2 (Oregon State Univ., Corvallis, OR, 1977), 313–346.Google Scholar
Deligne, P., ‘Le groupe fondamental de la droite projective moins trois points’, in Galois Groups over Q (Berkeley, CA, 1987), Math. Sci. Res. Inst. Publ., vol. 16 (Springer, New York, 1989), 79–297.CrossRefGoogle Scholar
Deligne, P., ‘Catégories tannakiennes’, in Progr. Math., vol. 87 (Birkäuser, Boston, 1990), 111–195.Google Scholar
Deligne, P. and Milne, J. S., ‘Tannakian categories’, in Hodge Cycles, Motives, and Shimura Varieties, LNM vol. 900 (1982), 101–228.CrossRefGoogle Scholar
Furusho, H., ‘ $p$ -adic multiple zeta values. II. Tannakian interpretations’, Amer. J. Math. 129(4) (2007), 1105–1144.CrossRefGoogle Scholar
Gross, B., ‘On the periods of abelian integrals and a formula of Chowla and Selberg’, Invent. Math. 45(2) (1978), 193–211.CrossRefGoogle Scholar
Haines, T., ‘Drinfeld–Plücker relations for homogeneous spaces, (affine) flag varieties, and Rapoport–Zink models’, unpublished.Google Scholar
Haines, T. and Jin, S., In preparation.Google Scholar
Imai, H., ‘On the Hodge groups of some abelian varieties’, Kodai Math. Sem. Rep. 27(3) (1976), 367–372.CrossRefGoogle Scholar
Jannsen, U., ‘Motives, numerical equivalence, and semi-simplicity’, Invent. Math. 107(3) (1992), 447–452.CrossRefGoogle Scholar
Katz, N. M., ‘ $p$ -adic $L$ -functions, Serre–Tate local moduli, and ratios of solutions of differential equations’, in Proceedings of the International Congress of Mathematicians (Helsinki, 1978) (Acad. Sci. Fennica, Helsinki, 1980), 365–371.Google Scholar
Kleiman, S., ‘Algebraic cycles and the Weil conjectures’, in Dix esposés sur la cohomologie des schémas (North-Holland, Amsterdam, 1968), 359–386.Google Scholar
Kahn, B., Murre, J. P. and Pedrini, C., ‘On the transcendental part of the motive of a surface’, in Algebraic Cycles and Motives. Vol. 2, London Math. Soc. Lecture Note Ser., vol. 344 (Cambridge Univ. Press, Cambridge, 2007), 143–202.CrossRefGoogle Scholar
Levine, M., ‘Tate motives and the vanishing conjectures for algebraic $K$ -theory’, in Algebraic $K$ -Theory and Algebraic Topology (Lake Louise, AB, 1991), volume 407 of NATO Adv. Sci. Inst. Ser. C: Math. Phys. Sci., vol. 407 (Kluwer Acad. Publ., Dordrecht, 1993), 167–188.Google Scholar
Lieberman, D. I., ‘Numerical and homological equivalence of algebraic cycles on Hodge manifolds’, Amer. J. Math. 90 (1968), 366–374.CrossRefGoogle Scholar
Mahler, K., ‘Ein Beweis der Transzendenz der $P$ -adischen Exponentialfunktion’, J. Reine Angew. Math. 169 (1933), 61–66.CrossRefGoogle Scholar
Milne, J., ‘The Tate conjecture over finite fields’, unpublished notes for a workshop of the American Institute for Mathematics in Palo Alto (2007).Google Scholar
Murty, V. K. and Patankar, V. M., ‘Splitting of abelian varieties’, Int. Math. Res. Not. IMRN (12) (2008), Art. ID rnn033.Google Scholar
Madapusi Pera, K., ‘The Tate conjecture for K3 surfaces in odd characteristic’, Invent. Math. 201(2) (2015), 625–668.CrossRefGoogle Scholar
Ogus, A., ‘A $p$ -adic analogue of the Chowla-Selberg formula’, in $p$ -adic Analysis (Trento, 1989), Lecture Notes in Math., vol. 1454 (Springer, Berlin, 1990), 319–341.Google Scholar
Ramón Marí, J. J., ‘On the Hodge conjecture for products of certain surfaces’, Collect. Math. 59(1) (2008), 1–26.CrossRefGoogle Scholar
Serre, J.-P., ‘Propriétés galoisiennes des points d’ordre fini des courbes elliptiques’, Invent. Math. 15(4) (1972), 259–331.CrossRefGoogle Scholar
Smirnov, O. N., ‘Graded associative algebras and Grothendieck standard conjectures’, Invent. Math. 128(1) (1997), 201–206.CrossRefGoogle Scholar
Spieß, M., ‘Proof of the Tate conjecture for products of elliptic curves over finite fields’, Math. Ann. 314(2) (1999), 285–290.Google Scholar
Tate, J., ‘Endomorphisms of abelian varieties over finite fields’, Invent. Math. 2 (1966), 134–144.CrossRefGoogle Scholar
Vezzani, A., ‘The relative (de-)perfectoidification functor and motivic $p$ -adic cohomologies’, in Perfectoid Spaces, Infosys Sci. Found. Ser. (2022), 15–36.CrossRefGoogle Scholar
Voevodsky, V., ‘Triangulated categories of motives over a field’, in Cycles, Transfers, and Motivic Homology Theories, Ann. of Math. Stud., vol. 143 (Princeton Univ. Press, Princeton, NJ, 2000), 188–238.Google Scholar
Waterhouse, W. C., Introduction to Affine Group Schemes, vol. 66 (Springer Science & Business Media, 2012).Google Scholar
Yamashita, G., ‘Bounds for the dimensions of $p$ -adic multiple $L$ -value spaces’, Doc. Math. (Extra vol.: Andrei A. Suslin sixtieth birthday) (2010), 687–723.Google Scholar