Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T03:02:20.894Z Has data issue: false hasContentIssue false
  • English
  • Français

TWISTED TRIPLE PRODUCT $\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  20 February 2019

Iván Blanco-Chacón  and
Michele Fornea
Iván Blanco-Chacón
Affiliation:
University College Dublin, Ireland ([email protected])
Michele Fornea
Affiliation:
McGill University, Montreal, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

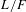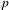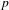Let $L/F$ be a quadratic extension of totally real number fields. For any prime $p$ unramified in $L$, we construct a $p$-adic $L$-function interpolating the central values of the twisted triple product $L$-functions attached to a 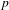$p$-nearly ordinary family of unitary cuspidal automorphic representations of 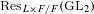$\text{Res}_{L\times F/F}(\text{GL}_{2})$. Furthermore, when 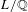$L/\mathbb{Q}$ is a real quadratic number field and 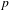$p$ is a split prime, we prove a 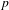$p$-adic Gross–Zagier formula relating the values of the 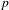$p$-adic $L$-function outside the range of interpolation to the syntomic Abel–Jacobi image of generalized Hirzebruch–Zagier cycles.

Keywords

twisted triple product L-functionssyntomic Abel–Jacobi mapHirzebruch–Zagier cycles

MSC classification

Primary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11G35: Varieties over global fields
Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 6 , November 2020 , pp. 1947 - 1992
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F. and Iovita, A., Triple product p-adic L-functions associated to finite slope p-adic families of modular forms, with an appendix by Eric Urban, Preprint, 2017, arXiv:1708.02785.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., Generalized Heegner cycles and p-adic Rankin L-series, Duke Math. J. 162(6) (2013), 1033–1148. With an appendix by Brian Conrad.10.1215/00127094-2142056Google Scholar
Besser, A., A generalization of Coleman’s p-adic integration theory, Invent. Math. 142(2) (2000), 397–434.10.1007/s002220000093Google Scholar
Blanco-Chacon, I. and Sols, I., p-adic Abel–Jacobi map and p-adic Gross–Zagier formula for Hilbert modular forms, Preprint, 2017, arXiv:1708.08950v1.Google Scholar
Bruinier, J. H., Burgos Gil, J. I. and Kühn, U., Borcherds products and arithmetic intersection theory on Hilbert modular surfaces., Duke Math. J. 139(1) (2007), 1–88.Google Scholar
Coleman, R. F., Classical and overconvergent modular forms, Invent. Math. 124(1–3) (1996), 215–241.10.1007/s002220050051Google Scholar
Darmon, H. and Rotger, V., Diagonal cycles and Euler systems I: A p-adic Gross-Zagier formula, Ann. Sci. Éc. Norm. Supér. (4) 47(4) (2014), 779–832.10.24033/asens.2227Google Scholar
Darmon, H. and Rotger, V., Diagonal cycles and Euler systems II: The Birch and Swinnerton-Dyer conjecture for Hasse–Weil–Artin L-functions, J. Amer. Math. Soc. 30(3) (2017), 601–672.Google Scholar
Deninger, C. and Murre, J., Motivic decomposition of abelian schemes and the Fourier transform, J. Reine Angew. Math. 422 (1991), 201–219.Google Scholar
Fornea, M., Twisted triple product p-adic L-functions and Hirzebruch–Zagier cycles, Preprint, 2017, arXiv:1710.03865.Google Scholar
Gan, W. T., Trilinear forms and triple product epsilon factors, Int. Math. Res. Not. IMRN 15 (2008), 15. Art. ID rnn058.Google Scholar
Harris, M. and Kudla, S. S., The central critical value of a triple product L-function, Ann. of Math. (2) 133(3) (1991), 605–672.10.2307/2944321Google Scholar
Hida, H., On nearly ordinary Hecke algebras for GL(2) over totally real fields, in Algebraic Number Theory, Advanced Studies in Pure Mathematics, Volume 17, pp. 139–169 (Academic Press, Boston, MA, 1989).Google Scholar
Hida, H., On p-adic L-functions of GL(2) × GL(2) over totally real fields, Ann. Inst. Fourier (Grenoble) 41(2) (1991), 311–391.Google Scholar
Hida, H., p-adic Automorphic Forms on Shimura Varieties, Springer Monographs in Mathematics, (Springer, New York, 2004).Google Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. I, II, Ann. of Math. (2) 79 (1964), 109–203. ibid. (2), 79: 205–326, 1964.Google Scholar
Hsieh, M.-L., Hida families and p-adic triple product L-functions, Preprint, 2017,arXiv:1705.02717.Google Scholar
Ichino, A., Trilinear forms and the central values of triple product L-functions, Duke Math. J. 145(2) (2008), 281–307.Google Scholar
Ishikawa, I., On the construction of twisted triple product $p$-adic $L$-functions, PhD thesis, 2017.Google Scholar
Katz, N. M., p-adic Properties of Modular Schemes and Modular Forms, Lecture Notes in Mathematics, Volume 350, pp. 69–190. (1973).Google Scholar
Katz, N. M., p-adic L-functions for CM fields, Invent. Math. 49(3) (1978), 199–297.Google Scholar
Kings, G., Higher regulators, Hilbert modular surfaces, and special values of L-functions, Duke Math. J. 92(1) (1998), 61–127.10.1215/S0012-7094-98-09202-XGoogle Scholar
Lan, K.-W., Arithmetic Compactifications of PEL-type Shimura Varieties, London Mathematical Society Monographs Series, Volume 36 (Princeton University Press, Princeton, NJ, 2013).Google Scholar
Lan, K.-W., Compactifications of PEL-type Shimura Varieties and Kuga families with ordinary loci, Preprint, 2017.Google Scholar
Lan, K.-W. and Polo, P., Dual BGG complexes for automorphic bundles, Math. Res. Lett. 25(1) (2018), 85–141.Google Scholar
Liu, Y., Hirzebruch-Zagier cycles and twisted triple product Selmer groups, Invent. Math. 205(3) (2016), 693–780.Google Scholar
Loeffler, D., Skinner, C. and Zerbes, S. L., Syntomic regulators of Asai–Flach classes, Preprint, 2016, arXiv:1608.06112.Google Scholar
Milne, J. S., Canonical models of (mixed) Shimura varieties and automorphic vector bundles, in Automorphic Forms, Shimura Varieties, and L-functions, Vol. I (Ann Arbor, MI, 1988), Perspect. Math., Volume 10, pp. 283–414 (Academic Press, Boston, MA, 1990).Google Scholar
Miyake, T., On automorphic forms on GL2 and Hecke operators, Ann. of Math. (2) 94 (1971), 174–189.Google Scholar
Nekovár, J., Eichler–Shimura relations and semisimplicity of étale cohomology of quaternionic Shimura varieties, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 1179–1252.Google Scholar
Piatetski-Shapiro, I. and Rallis, S., Rankin triple L functions, Compos. Math. 64(1) (1987), 31–115.Google Scholar
Prasad, D., Trilinear forms for representations of GL(2) and local 𝜖-factors, Compos. Math. 75(1) (1990), 1–46.Google Scholar
Prasad, D., Invariant forms for representations of GL2 over a local field, Amer. J. Math. 114(6) (1992), 1317–1363.Google Scholar
Prasad, D. and Schulze-Pillot, R., Generalised form of a conjecture of Jacquet and a local consequence, J. Reine Angew. Math. 616 (2008), 219–236.Google Scholar
Rapoport, M., Compactifications de l’espace de modules de Hilbert–Blumenthal, Compos. Math. 36(3) (1978), 255–335.Google Scholar
Scholl, A. J., Motives for modular forms, Invent. Math. 100(2) (1990), 419–430.Google Scholar
Shimura, G., The special values of the zeta functions associated with Hilbert modular forms, Duke Math. J. 45(3) (1978), 637–679.Google Scholar
Tian, Y. and Xiao, L., p-adic cohomology and classicality of overconvergent Hilbert modular forms, Astérisque 382 (2016), 73–162.Google Scholar
Voevodsky, V., Triangulated categories of motives over a field, in Cycles, Transfers, and Motivic Homology Theories, Annals of Mathematics Studies, Volume 143, pp. 188–238 (Princeton University Press, Princeton, NJ, 2000).Google Scholar
Wildeshaus, J., Chow motives without projectivity, Compos. Math. 145(5) (2009), 1196–1226.Google Scholar
Wildeshaus, J., On the interior motive of certain Shimura varieties: the case of Hilbert–Blumenthal varieties, Int. Math. Res. Not. IMRN 10 (2012), 2321–2355.Google Scholar