Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-14T12:06:18.976Z Has data issue: false hasContentIssue false
  • English
  • Français

TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS

Part of: Surfaces and higher-dimensional varieties Local theory General commutative ring theory

Published online by Cambridge University Press:  13 January 2016

Alberto Chiecchio ,
Florian Enescu ,
Lance Edward Miller  and
Karl Schwede
Alberto Chiecchio
Affiliation:
TASIS, Dorado, Puerto Rico ([email protected])
Florian Enescu
Affiliation:
Department of Mathematics and Statistics, Georgia State University, Atlanta GA 30303, USA ([email protected])
Lance Edward Miller
Affiliation:
Department of Mathematical Sciences, University of Arkansas, Fayetteville, AR 72701, USA ([email protected])
Karl Schwede
Affiliation:
Department of Mathematics, University of Utah, 155 S 1400 E Room 233, Salt Lake City, UT, 84112, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

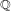Many results are known about test ideals and $F$-singularities for $\mathbb{Q}$-Gorenstein rings. In this paper, we generalize many of these results to the case when the symbolic Rees algebra 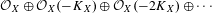${\mathcal{O}}_{X}\oplus {\mathcal{O}}_{X}(-K_{X})\oplus {\mathcal{O}}_{X}(-2K_{X})\oplus \cdots \,$ is finitely generated (or more generally, in the log setting for $-K_{X}-\unicode[STIX]{x1D6E5}$). 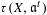In particular, we show that the $F$-jumping numbers of $\unicode[STIX]{x1D70F}(X,\mathfrak{a}^{t})$ are discrete and rational. We show that test ideals 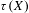$\unicode[STIX]{x1D70F}(X)$ can be described by alterations as in Blickle–Schwede–Tucker (and hence show that splinters are strongly $F$-regular in this setting – recovering a result of Singh). We demonstrate that multiplier ideals reduce to test ideals under reduction modulo 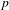$p$ when the symbolic Rees algebra is finitely generated. We prove that Hartshorne–Speiser–Lyubeznik–Gabber-type stabilization still holds. We also show that test ideals satisfy global generation properties in this setting.

Keywords

Anti-canonicaltest idealmultiplier ideal

MSC classification

Primary: 14J17: Singularities 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 14B05: Singularities
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 1 , February 2018 , pp. 171 - 206
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aberbach, I. M. and MacCrimmon, B., Some results on test elements, Proc. Edinb. Math. Soc. (2) 42(3) (1999), 541–549, MR 1721770 (2000i:13005).CrossRefGoogle Scholar
Bhatt, B., Derived splinters in positive characteristic, Compos. Math. 148(6) (2012), 1757–1786, MR 2999303.Google Scholar
Birkar, C., Existence of flips and minimal models for 3-folds in char $p$ , Annales Scientifiques de l’ENS, to appear, 2013, arXiv:1311.3098.Google Scholar
Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23(2) (2010), 405–468, MR 2601039 (2011f:14023).Google Scholar
Birkar, C. and Waldron, J., Existence of Mori fibre spaces for 3-folds in char $p$ , Preprint, 2014, arXiv:1410.4511.Google Scholar
Blickle, M., Test ideals via algebras of p -e -linear maps, J. Algebraic Geom. 22(1) (2013), 49–83, MR 2993047.CrossRefGoogle Scholar
Blickle, M., Mustaţǎ, M. and Smith, K. E., Discreteness and rationality of F-thresholds, Michigan Math. J. 57 (2008), 43–61, special volume in honor of Melvin Hochster MR 2492440 (2010c:13003).Google Scholar
Blickle, M., Mustaţă, M. and Smith, K. E., F-thresholds of hypersurfaces, Trans. Amer. Math. Soc. 361(12) (2009), 6549–6565, MR 2538604 (2011a:13006).CrossRefGoogle Scholar
Blickle, M. and Schwede, K., p -1 -linear maps in algebra and geometry, in Commutative Algebra, pp. 123–205 (Springer, New York, 2013).CrossRefGoogle Scholar
Blickle, M., Schwede, K., Takagi, S. and Zhang, W., Discreteness and rationality of F-jumping numbers on singular varieties, Math. Ann. 347(4) (2010), 917–949, MR 2658149.Google Scholar
Blickle, M., Schwede, K. and Tucker, K., F-singularities via alterations, Amer. J. Math. 137(1) (2015), 61–109, MR 3318087.Google Scholar
Boucksom, S., de Fernex, T., Favre, C. and Urbinati, S., Valuation spaces and multiplier ideals on singular varieties, in Recent Advances in Algebraic Geometry, London Math. Soc. Lecture Note Ser., Volume 417, pp. 29–51 (Cambridge University Press, Cambridge, 2015), MR 3380442.CrossRefGoogle Scholar
Cascini, P., Tanaka, H. and Xu, C., On base point freeness in positive characteristic, Preprint, 2013, arXiv:1305.3502.Google Scholar
Chiecchio, A., About a Minimal Model Program without flips, Preprint, 2014, arXiv:1410.6230.Google Scholar
Chiecchio, A. and Urbinati, S., Ample Weil divisors, J. Algebra 437 (2015), 202–221, MR 3351963.Google Scholar
Cutkosky, S., Weil divisors and symbolic algebras, Duke Math. J. 57(1) (1988), 175–183, MR 952230 (89e:14003).Google Scholar
de Fernex, T., Docampo, R., Takagi, S. and Tucker, K., Comparing multiplier ideals to test ideals on numerically ℚ-Gorenstein varieties, Bull. Lond. Math. Soc. 47(2) (2015), 359–369, MR 3335128.Google Scholar
De Fernex, T. and Hacon, C., Singularities on normal varieties, Compos. Math. 145(2) (2009), 393–414.Google Scholar
Demazure, M., Anneaux gradués normaux, in Introduction à la théorie des singularités, II, Travaux en Cours, Volume 37, pp. 35–68 (Hermann, Paris, 1988).Google Scholar
Ein, L., Lazarsfeld, R., Smith, K. E. and Varolin, D., Jumping coefficients of multiplier ideals, Duke Math. J. 123(3) (2004), 469–506, MR 2068967 (2005k:14004).CrossRefGoogle Scholar
Fujino, O., Schwede, K. and Takagi, S., Supplements to non-lc ideal sheaves, in Higher Dimensional Algebraic Geometry, pp. 1–47 (Res. Inst. Math. Sci. (RIMS), Kyoto, 2011).Google Scholar
Gabber, O., Notes on some t-structures, in Geometric aspects of Dwork theory. Vol. I, II, pp. 711–734 (Walter de Gruyter GmbH & Co. KG, Berlin, 2004).Google Scholar
Goto, S., Herrmann, M., Nishida, K. and Villamayor, O., On the structure of Noetherian symbolic Rees algebras, Manuscripta Math. 67(2) (1990), 197–225, MR 1042238 (91a:13006).Google Scholar
Hacon, C. D. and Xu, C., On the three dimensional minimal model program in positive characteristic, J. Amer. Math. Soc. 28(3) (2015), 711–744, MR 3327534.Google Scholar
Hara, N., Geometric interpretation of tight closure and test ideals, Trans. Amer. Math. Soc. 353(5) (2001), 1885–1906, (electronic) MR 1813597 (2001m:13009).Google Scholar
Hara, N. and Yoshida, K.-I., A generalization of tight closure and multiplier ideals, Trans. Amer. Math. Soc. 355(8) (2003), 3143–3174, (electronic) MR 1974679 (2004i:13003).Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, No. 52, (Springer-Verlag, New York, 1977), MR 0463157 (57 #3116).Google Scholar
Hartshorne, R., Generalized divisors on Gorenstein schemes, in Proceedings of Conference on Algebraic Geometry and Ring Theory in honor of Michael Artin, Part III (Antwerp, 1992), Volume 8, pp. 287–339. (1994).Google Scholar
Hartshorne, R. and Speiser, R., Local cohomological dimension in characteristic p , Ann. of Math. (2) 105(1) (1977), 45–79, MR 0441962 (56 #353).Google Scholar
Hochster, M., Foundations of tight closure theory, in Lecture Notes from a Course Taught on the University of Michigan Fall 2007 (2007).Google Scholar
Hochster, M. and Huneke, C., Tight closure, invariant theory, and the Briançon–Skoda theorem, J. Amer. Math. Soc. 3(1) (1990), 31–116, MR 1017784 (91g:13010).Google Scholar
Hochster, M. and Huneke, C., Infinite integral extensions and big Cohen–Macaulay algebras, Ann. of Math. (2) 135(1) (1992), 53–89, MR 1147957 (92m:13023).Google Scholar
Hochster, M. and Huneke, C., F-regularity, test elements, and smooth base change, Trans. Amer. Math. Soc. 346(1) (1994), 1–62, MR 1273534 (95d:13007).Google Scholar
Huneke, C. and Lyubeznik, G., Absolute integral closure in positive characteristic, Adv. Math. 210(2) (2007), 498–504, MR 2303230 (2008d:13005).Google Scholar
de Jong, A. J., Smoothness, semi-stability and alterations, Inst. Hautes Études Sci. Publ. Math. (83) (1996), 51–93, MR 1423020 (98e:14011).Google Scholar
Katzman, M., Lyubeznik, G. and Zhang, W., On the discreteness and rationality of F-jumping coefficients, J. Algebra 322(9) (2009), 3238–3247, MR 2567418 (2011c:13005).Google Scholar
Katzman, M., Schwede, K., Singh, A. K. and Zhang, W., Rings of Frobenius operators, Math. Proc. Cambridge Philos. Soc. 157(1) (2014), 151–167, MR 3211813.Google Scholar
Kollár, J., Exercises in the birational geometry of algebraic varieties, Preprint, 2008,arXiv:0809.2579.Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, Volume 134 (Cambridge University Press, Cambridge, 1998), With the collaboration of C. H. Clemens and A. Corti, Translated from the 1998 Japanese original MR 1658959 (2000b:14018).Google Scholar
Kunz, E., On Noetherian rings of characteristic p , Amer. J. Math. 98(4) (1976), 999–1013, MR 0432625 (55 #5612).CrossRefGoogle Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. I, in Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Classical Setting: Line Bundles and Linear Series, Volume 48 (Springer-Verlag, Berlin, 2004), MR 2095471 (2005k:14001a).Google Scholar
Lipman, J., Rational singularities, with applications to algebraic surfaces and unique factorization, Inst. Hautes Études Sci. Publ. Math. (36) (1969), 195–279, MR 0276239 (43 #1986).Google Scholar
Lyubeznik, G., F-modules: applications to local cohomology and D-modules in characteristic p > 0, J. Reine Angew. Math. 491 (1997), 65–130, MR 1476089 (99c:13005).Google Scholar
Lyubeznik, G. and Smith, K. E., Strong and weak F-regularity are equivalent for graded rings, Amer. J. Math. 121(6) (1999), 1279–1290, MR 1719806 (2000m:13006).Google Scholar
Lyubeznik, G. and Smith, K. E., On the commutation of the test ideal with localization and completion, Trans. Amer. Math. Soc. 353(8) (2001), 3149–3180, (electronic) MR 1828602 (2002f:13010).Google Scholar
Mustaţă, M., The non-nef locus in positive characteristic, in A Celebration of Algebraic Geometry, Clay Math. Proc., Volume 18, pp. 535–551 (Amer. Math. Soc., Providence, RI, 2013).Google Scholar
Pérez, F., On the constancy regions for mixed test ideals, J. Algebra 396 (2013), 82–97, MR 3108073.Google Scholar
Schwede, K., F-adjunction, Algebra Number Theory 3(8) (2009), 907–950, MR 2587408 (2011b:14006).Google Scholar
Schwede, K., Test ideals in non-ℚ-Gorenstein rings, Trans. Amer. Math. Soc. 363(11) (2011), 5925–5941.Google Scholar
Schwede, K. and Smith, K. E., Globally F-regular and log Fano varieties, Adv. Math. 224(3) (2010), 863–894, MR 2628797 (2011e:14076).Google Scholar
Schwede, K. and Tucker, K., On the behavior of test ideals under finite morphisms, J. Algebraic Geom. 23(3) (2014a), 399–443, MR 3205587.Google Scholar
Schwede, K. and Tucker, K., Test ideals of non-principal ideals: Computations, jumping numbers, alterations and division theorems, J. Math. Pures Appl. (9) 102(5) (2014b), 891–929, MR 3271293.Google Scholar
Schwede, K., Tucker, K. and Zhang, W., Test ideals via a single alteration and discreteness and rationality of F-jumping numbers, Math. Res. Lett. 19(01) (2012), 191–197.Google Scholar
Singh, A. K., Q -Gorenstein splinter rings of characteristic p are F-regular, Math. Proc. Cambridge Philos. Soc. 127(2) (1999), 201–205, MR 1735920 (2000j:13006).Google Scholar
Singh, A. K., Private communication, 2001–2014.Google Scholar
Smith, K. E., The multiplier ideal is a universal test ideal, Comm. Algebra 28(12) (2000), 5915–5929, Special issue in honor of Robin Hartshorne MR 1808611 (2002d:13008).Google Scholar
Takagi, S., An interpretation of multiplier ideals via tight closure, J. Algebraic Geom. 13(2) (2004), 393–415, MR 2047704 (2005c:13002).Google Scholar
Watanabe, K., Some remarks concerning Demazure’s construction of normal graded rings, Nagoya Math. J. 83 (1981), 203–211, MR 632654 (83g:13016).Google Scholar
Xu, C., On the base-point-free theorem of 3-folds in positive characteristic, J. Inst. Math. Jussieu 14(3) (2015), 577–588, MR 3352529.Google Scholar