Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-29T19:01:33.467Z Has data issue: false hasContentIssue false
  • English
  • Français

PRESCRIBED VIRTUAL HOMOLOGICAL TORSION OF 3-MANIFOLDS

Published online by Cambridge University Press:  08 June 2022

Michelle Chu Open the ORCID record for Michelle Chu [Opens in a new window]  and
Daniel Groves
Michelle Chu*
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, 322 Science and Engineering Offices (M/C 249), 851 S. Morgan St., Chicago, IL 60607-7045 ([email protected])
Daniel Groves
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, 322 Science and Engineering Offices (M/C 249), 851 S. Morgan St., Chicago, IL 60607-7045 ([email protected])
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let M be an irreducible 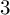$3$-manifold M with empty or toroidal boundary which has at least one hyperbolic piece in its geometric decomposition, and let A be a finite abelian group. Generalizing work of Sun [20] and of Friedl–Herrmann [7], we prove that there exists a finite cover 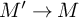$M' \to M$ so that A is a direct factor in 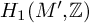$H_1(M',{\mathbb Z})$.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 6 , November 2023 , pp. 2931 - 2941
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agol, I., ‘Systoles of hyperbolic 4-manifolds’, Preprint, 2006, arXiv:0612290.Google Scholar
Agol, I., ‘The virtual Haken conjecture’, Doc. Math. 18 (2013) 1045–1087, With an appendix by Agol, Daniel Groves, and Jason Manning.Google Scholar
Bergeron, N., Haglund, F. and Wise, D. T., ‘Hyperplane sections in arithmetic hyperbolic manifolds’, J. Lond. Math. Soc. (2) 83(2) (2011), 431–448.CrossRefGoogle Scholar
Belolipetsky, M. V. and Thomson, S. A., ‘Systoles of hyperbolic manifolds’, Algebr. Geom. Topol. 11(3) (2011), 1455–1469.10.2140/agt.2011.11.1455CrossRefGoogle Scholar
Coornaert, M., Delzant, T. and Papadopoulos, A., Géométrie et théorie des groupes: Les groupes hyperboliques de Gromov, Lecture Notes in Mathematics, Vol. 1441 (Springer-Verlag, Berlin, 1990).10.1007/BFb0084913CrossRefGoogle Scholar
Cooper, D. and Futer, D., ‘Ubiquitous quasi-Fuchsian surfaces in cusped hyperbolic 3-manifolds’, Geom. Topol. 23(1) (2019), 241–298.CrossRefGoogle Scholar
Friedl, S. and Herrmann, G., ‘Torsion in the homology of finite covers of 3-manifolds’, Preprint, 2017, arXiv:1710.08983.Google Scholar
Gromov, M. and Piatetski-Shapiro, I., ‘Nonarithmetic groups in Lobachevsky spaces’, Inst. Hautes Études Sci. Publ. Math. (66) (1988), 93–103.10.1007/BF02698928CrossRefGoogle Scholar
Gangolli, R. and Warner, G., ‘Zeta functions of Selberg’s type for some noncompact quotients of symmetric spaces of rank one’, Nagoya Math. J., 78 (1980), 1–44.10.1017/S002776300001878XCrossRefGoogle Scholar
Hadari, A., ‘Every infinite order mapping class has an infinite order action on the homology of some finite cover’, Preprint, 2015, arXiv:1508.01555.Google Scholar
Christopher Hruska, G., ‘Relative hyperbolicity and relative quasiconvexity for countable groups’, Algebr. Geom. Topol. 10(3) (2010), 1807–1856.10.2140/agt.2010.10.1807CrossRefGoogle Scholar
Haglund, F. and Wise, D. T., ‘Special cube complexes’, Geom. Funct. Anal. 17(5) (2008), 1551–1620.10.1007/s00039-007-0629-4CrossRefGoogle Scholar
Hruska, G. C. and Wise, D. T., ‘Finiteness properties of cubulated groups’, Compos. Math. 150(3) (2014), 453–506.CrossRefGoogle Scholar
Kahn, J. and Markovic, V., ‘Immersing almost geodesic surfaces in a closed hyperbolic three manifold’, Ann. of Math. (2) 175(3) (2012), 1127–1190.CrossRefGoogle Scholar
Kahn, J. and Wright, A., ‘Nearly Fuchsian surface subgroups of finite covolume Kleinian groups’, Duke Math. J. 170(3) (2021), 503–573.CrossRefGoogle Scholar
Liu, Y., ‘Virtual homological spectral radii for automorphisms of surfaces’, J. Amer. Math. Soc. 33(4) (2020), 1167–1227.10.1090/jams/949CrossRefGoogle Scholar
Maskit, B., ‘On Klein’s combination theorem’. IV’, Trans. Amer. Math. Soc. 336(1) (1993), 265–294.Google Scholar
Margulis, G., Mohammadi, A. and Oh, H., ‘Closed geodesics and holonomies for Kleinian manifolds’, Geom. Funct. Anal. 24(5) (2014), 1608–1636.10.1007/s00039-014-0299-yCrossRefGoogle Scholar
Przytycki, P. and Wise, D. T., ‘Mixed 3-manifolds are virtually special’, J. Amer. Math. Soc. 31(2) (2018), 319–347.10.1090/jams/886CrossRefGoogle Scholar
Sun, H., ‘Virtual homological torsion of closed hyperbolic 3-manifolds’, J. Differential Geom. 100(3) (2015), 547–583.CrossRefGoogle Scholar
Sageev, M. and Wise, D. T., ‘Cores for quasiconvex actions’, Proc. Amer. Math. Soc. 143(7) (2015), 2731–2741.10.1090/S0002-9939-2015-12297-6CrossRefGoogle Scholar
Wise, D. T., The Structure of Groups with a Quasiconvex Hierarchy , Annals of Mathematics Studies, Vol. 209 (Princeton University Press, Princeton, NJ, 2021).Google Scholar