PARABOLIC COMPACTIFICATION OF HOMOGENEOUS SPACES

Abstract

In this article, we study compactifications of homogeneous spaces coming from equivariant, open embeddings into a generalized flag manifold 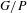$G/P$. The key to this approach is that in each case 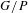$G/P$ is the homogeneous model for a parabolic geometry; the theory of such geometries provides a large supply of geometric tools and invariant differential operators that can be used for this study. A classical theorem of Wolf shows that any involutive automorphism of a semisimple Lie group 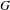$G$ with fixed point group 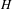$H$ gives rise to a large family of such compactifications of homogeneous spaces of 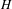$H$. Most examples of (classical) Riemannian symmetric spaces as well as many non-symmetric examples arise in this way. A specific feature of the approach is that any compactification of that type comes with the notion of ‘curved analog’ to which the tools we develop also apply. The model example of this is a general Poincaré–Einstein manifold forming the curved analog of the conformal compactification of hyperbolic space. In the first part of the article, we derive general tools for the analysis of such compactifications. In the second part, we analyze two families of examples in detail, which in particular contain compactifications of the symmetric spaces 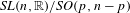$\mathit{SL}(n,\mathbb{R})/\mathit{SO}(p,n-p)$ and $\mathit{SO}(n,\mathbb{C})/\mathit{SO}(n)$. We describe the decomposition of the compactification into orbits, show how orbit closures can be described as the zero sets of smooth solutions to certain invariant differential operators and prove a local slice theorem around each orbit in these examples.