Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T04:34:14.488Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NUMBER OF DEDEKIND CUTS AND TWO-CARDINAL MODELS OF DEPENDENT THEORIES

Published online by Cambridge University Press:  23 January 2015

Artem Chernikov  and
Saharon Shelah
Artem Chernikov
Affiliation:
Institut de Mathématiques de Jussieu - Paris Rive Gauche
Saharon Shelah
Affiliation:
Hebrew University of Jerusalem
Get access Rights & Permissions [Opens in a new window]

Abstract

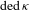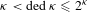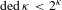For an infinite cardinal ${\it\kappa}$, let $\text{ded}\,{\it\kappa}$ denote the supremum of the number of Dedekind cuts in linear orders of size ${\it\kappa}$. It is known that ${\it\kappa}<\text{ded}\,{\it\kappa}\leqslant 2^{{\it\kappa}}$ for all ${\it\kappa}$ and that $\text{ded}\,{\it\kappa}<2^{{\it\kappa}}$ is consistent for any ${\it\kappa}$ of uncountable cofinality. We prove however that 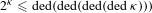$2^{{\it\kappa}}\leqslant \text{ded}(\text{ded}(\text{ded}(\text{ded}\,{\it\kappa})))$ always holds. Using this result we calculate the Hanf numbers for the existence of two-cardinal models with arbitrarily large gaps and for the existence of arbitrarily large models omitting a type in the class of countable dependent first-order theories. Specifically, we show that these bounds are as large as in the class of all countable theories.

Keywords

Dedekind cutslinear orderstreescardinal arithmeticPCFtwo-cardinal modelsomitting typesdependent theoriesNIP
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 4 , October 2016 , pp. 771 - 784
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baumgartner, J. E., Almost-disjoint sets, the dense set problem and the partition calculus, Ann. Math. Logic 9(4) (1976), 401–439.CrossRefGoogle Scholar
Bays, T., Some two-cardinal results for o-minimal theories, J. Symbolic Logic 63(2) (1998), 543–548.CrossRefGoogle Scholar
Berenstein, A. and Shami, Z., Invariant version of cardinality quantifiers in superstable theories, Notre Dame J. Form. Logic 47(3) (2006), 343–351 (electronic).Google Scholar
Chernikov, A., Kaplan, I. and Shelah, S., On non-forking spectra, Preprint, arXiv:1205.3101v1, 2012.Google Scholar
Chernikov, A. and Simon, P., Externally definable sets and dependent pairs II, Trans. of AMS. accepted.Google Scholar
Chernikov, A. and Simon, P., Externally definable sets and dependent pairs, Israel J. Math. 194(1) (2013), 409–425.CrossRefGoogle Scholar
Gitik, M. and Shelah, S., On certain indestructibility of strong cardinals and a question of Hajnal, Arch. Math. Logic 28(1) (1989), 35–42.CrossRefGoogle Scholar
Haskell, D., Hrushovski, E. and Macpherson, D., Stable Domination and Independence in Algebraically Closed Valued Fields, Lecture Notes in Logic, Volume 30 (Association for Symbolic Logic, Chicago, IL, 2008).Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, Volume 42 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Hrushovski, E. and Pillay, A., On NIP and invariant measures, J. Eur. Math. Soc. (JEMS) 13(4) (2011), 1005–1061.Google Scholar
Hrushovski, E. and Shelah, S., Stability and omitting types, Israel J. Math. 74(2-3) (1991), 289–321.CrossRefGoogle Scholar
Holz, M., Steffens, K. and Weitz, E., Introduction to Cardinal Arithmetic, Birkhäuser Advanced Texts: Basler Lehrbücher [Birkhäuser Advanced Texts: Basel Textbooks], (Birkhäuser Verlag, Basel, 1999).CrossRefGoogle Scholar
Jerome Keisler, H., Six classes of theories, J. Aust. Math. Soc. Ser. A 21(3) (1976), 257–266.CrossRefGoogle Scholar
Kaplan, I. and Shelah, S., A dependent theory with few indiscernibles, Israel J. Math. 202(1) (2014), 59–103.CrossRefGoogle Scholar
Kaplan, I. and Shelah, S., Examples in dependent theories, Preprint, arXiv:1009.5420, 2010.Google Scholar
Lachlan, A. H., A property of stable theories, Fund. Math. 77(1) (1972), 9–20.CrossRefGoogle Scholar
Marker, D., Omitting types in o-minimal theories, J. Symbolic Logic 51(1) (1986), 63–74.CrossRefGoogle Scholar
Mitchell, W., Aronszajn trees and the independence of the transfer property, Ann. Math. Logic 5 (1972/73), 21–46.CrossRefGoogle Scholar
Shelah, S., Classification Theory and the Number of Nonisomorphic Models, second edition, Studies in Logic and the Foundations of Mathematics, Volume 92 (North-Holland Publishing Co., Amsterdam, 1990).Google Scholar
Shelah, S., More on cardinal arithmetic, Arch. Math. Logic 32(6) (1993), 399–428.CrossRefGoogle Scholar
Shelah, S., Cardinal Arithmetic, Oxford Logic Guides, Volume 29 (The Clarendon Press Oxford University Press, New York, 1994). Oxford Science Publications.CrossRefGoogle Scholar
Shelah, S., Further cardinal arithmetic, Israel J. Math. 95 (1996), 61–114. doi:10.1007/BF02761035.CrossRefGoogle Scholar
Shelah, S., Strongly dependent theories, Preprint, arXiv:math/0504197, 2005.Google Scholar
Shelah, S., Dependent theories and the generic pair conjecture, Preprint, arXiv:math/0702292, 2007.Google Scholar
Shelah, S., Dependent first order theories, continued, Israel J. Math. 173 (2009), 1–60.CrossRefGoogle Scholar
Shelah, S., Dependent dreams: recounting types, Preprint, arXiv:1202.5795, 2012.Google Scholar