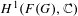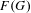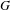Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bailet, Pauline
Dimca, Alexandru
and
Yoshinaga, Masahiko
2018.
A vanishing result for the first twisted cohomology of affine varieties and applications to line arrangements.
manuscripta mathematica,
Vol. 157,
Issue. 3-4,
p.
497.