Article contents
NORMAL FUNCTIONALS ON LIPSCHITZ SPACES ARE WEAK* CONTINUOUS
Published online by Cambridge University Press: 08 April 2021
Abstract
Let
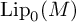 $\mathrm {Lip}_0(M)$
be the space of Lipschitz functions on a complete metric space M that vanish at a base point. We prove that every normal functional in
$\mathrm {Lip}_0(M)$
be the space of Lipschitz functions on a complete metric space M that vanish at a base point. We prove that every normal functional in
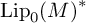 ${\mathrm {Lip}_0(M)}^*$
is weak* continuous; that is, in order to verify weak* continuity it suffices to do so for bounded monotone nets of Lipschitz functions. This solves a problem posed by N. Weaver. As an auxiliary result, we show that the series decomposition developed by N. J. Kalton for functionals in the predual of
${\mathrm {Lip}_0(M)}^*$
is weak* continuous; that is, in order to verify weak* continuity it suffices to do so for bounded monotone nets of Lipschitz functions. This solves a problem posed by N. Weaver. As an auxiliary result, we show that the series decomposition developed by N. J. Kalton for functionals in the predual of
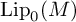 $\mathrm {Lip}_0(M)$
can be partially extended to
$\mathrm {Lip}_0(M)$
can be partially extended to
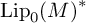 ${\mathrm {Lip}_0(M)}^*$
.
${\mathrm {Lip}_0(M)}^*$
.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 2093 - 2102
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 1
- Cited by



