Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T08:48:36.784Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLICITY ONE AT FULL CONGRUENCE LEVEL

Part of: Representation theory of groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  15 May 2020

Daniel Le Open the ORCID record for Daniel Le [Opens in a new window] ,
Stefano Morra  and
Benjamin Schraen
Daniel Le
Affiliation:
University of Toronto, 40 St. George Street, Toronto, ONM5S 2E4 ([email protected])
Stefano Morra
Affiliation:
Université Paris 8, Laboratoire d’Analyse, Géométrie et Applications, LAGA, Université Sorbonne Paris Nord, CNRS, UMR 7539, F-93430, Villetaneuse, France ([email protected])
Benjamin Schraen
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire de mathématiques dOrsay, 91405, Orsay, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $F$ be a totally real field in which 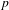$p$ is unramified. Let $\overline{r}:G_{F}\rightarrow \text{GL}_{2}(\overline{\mathbf{F}}_{p})$ be a modular Galois representation that satisfies the Taylor–Wiles hypotheses and is tamely ramified and generic at a place $v$ above 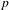$p$. Let 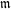$\mathfrak{m}$ be the corresponding Hecke eigensystem. We describe the 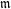$\mathfrak{m}$-torsion in the 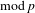$\text{mod}\,p$ cohomology of Shimura curves with full congruence level at $v$ as a 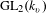$\text{GL}_{2}(k_{v})$-representation. In particular, it only depends on 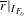$\overline{r}|_{I_{F_{v}}}$ and its Jordan–Hölder factors appear with multiplicity one. The main ingredients are a description of the submodule structure for generic 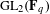$\text{GL}_{2}(\mathbf{F}_{q})$-projective envelopes and the multiplicity one results of Emerton, Gee and Savitt [Lattices in the cohomology of Shimura curves, Invent. Math. 200(1) (2015), 1–96].

Keywords

multiplicity onecohomology of Shimura curvesmod p Langlands programmodular representations of GL2(Fq)

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 11F80: Galois representations 20C33: Representations of finite groups of Lie type
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 2 , March 2022 , pp. 637 - 658
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, N., Henniart, G., Herzig, F. and Vignéras, M.-F., A classification of irreducible admissible mod p representations of p-adic reductive groups, J. Amer. Math. Soc. 30(2) (2017), 495–559.CrossRefGoogle Scholar
Breuil, C., The emerging p-adic Langlands programme, in Proceedings of the International Congress of Mathematicians. Volume II, pp. 203–230 (Hindustan Book Agency, New Delhi, 2010).Google Scholar
Breuil, C., Sur un problème de compatibilité local-global modulo p pour GL2 , J. Reine Angew. Math. 692 (2014), 1–76.CrossRefGoogle Scholar
Breuil, C. and Diamond, F., Formes modulaires de Hilbert modulo p et valeurs d’extensions entre caractères galoisiens, Ann. Sci. Éc. Norm. Supér. (4) 47(5) (2014), 905–974.10.24033/asens.2230CrossRefGoogle Scholar
Breuil, C. and Paškūnas, V., Towards a modulo p Langlands correspondence for GL2 , Mem. Amer. Math. Soc. 216(1016) (2012), vi+114.Google Scholar
Buzzard, K., Diamond, F. and J. Vis., F., On Serre’s conjecture for mod ℓ Galois representations over totally real fields, Duke Math. J. 155(1) (2010), 105–161.CrossRefGoogle Scholar
Colmez, P., Représentations de GL2(Q p) et (𝜙, 𝛤)-modules, Astérisque 330 (2010), 281–509.Google Scholar
Emerton, M., ‘Local-global compatibility in the $p$ -adic langlands program for $\text{GL}_{2}/\mathbf{Q}$ ’, Preprint, 2011, http://www.math.uchicago.edu/∼emerton/pdffiles/lg.pdf.Google Scholar
Emerton, M., Gee, T. and Savitt, D., Lattices in the cohomology of Shimura curves, Invent. Math. 200(1) (2015), 1–96.CrossRefGoogle Scholar
Gee, T., Automorphic lifts of prescribed types, Math. Ann. 350(1) (2011), 107–144.Google Scholar
Gee, T., On the weights of mod p Hilbert modular forms, Invent. Math. 184(1) (2011), 1–46.CrossRefGoogle Scholar
Gee, T., Herzig, F. and Savitt, D., General Serre weight conjectures, J. Eur. Math. Soc. (JEMS) 20(12) (2018), 2859–2949.CrossRefGoogle Scholar
Gee, T. and Kisin, M., The Breuil–Mézard conjecture for potentially Barsotti-Tate representations, Forum Math. Pi 2(e1) (2014), 56 pp.10.1017/fmp.2014.1CrossRefGoogle Scholar
Herzig, F., The weight in a Serre-type conjecture for tame n-dimensional Galois representations, Duke Math. J. 149(1) (2009), 37–116.CrossRefGoogle Scholar
Hu, Y., Sur quelques représentations supersingulières de GL2(ℚp f ), J. Algebra 324(7) (2010), 1577–1615.10.1016/j.jalgebra.2010.06.006CrossRefGoogle Scholar
Hu, Y. and Wang, H., Multiplicity one for the mod p cohomology of Shimura curves: the tame case, Math. Res. Lett. 25(3) (2018), 843–873.CrossRefGoogle Scholar
Jantzen, J. C., Representations of Algebraic Groups, 2nd ed., Mathematical Surveys and Monographs, 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Le, D., Le Hung, B. V., Levin, B. and Morra, S., Serre weights and Breuil’s lattice conjectures in dimension three, Forum Math. Pi 8 (2020), e5.CrossRefGoogle Scholar
Paškūnas, V., The image of Colmez’s Montreal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191.CrossRefGoogle Scholar
Pillen, C., Reduction modulo p of some Deligne-Lusztig characters, Arch. Math. (Basel) 61(5) (1993), 421–433.CrossRefGoogle Scholar