Article contents
MOMENTS AND HYBRID SUBCONVEXITY FOR SYMMETRIC-SQUARE L-FUNCTIONS
Published online by Cambridge University Press: 06 December 2021
Abstract
We establish sharp bounds for the second moment of symmetric-square L-functions attached to Hecke Maass cusp forms 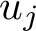 $u_j$ with spectral parameter
$u_j$ with spectral parameter 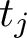 $t_j$, where the second moment is a sum over
$t_j$, where the second moment is a sum over 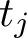 $t_j$ in a short interval. At the central point
$t_j$ in a short interval. At the central point 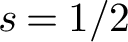 $s=1/2$ of the L-function, our interval is smaller than previous known results. More specifically, for
$s=1/2$ of the L-function, our interval is smaller than previous known results. More specifically, for 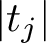 $\left \lvert t_j\right \rvert $ of size T, our interval is of size
$\left \lvert t_j\right \rvert $ of size T, our interval is of size 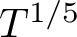 $T^{1/5}$, whereas the previous best was
$T^{1/5}$, whereas the previous best was 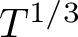 $T^{1/3}$, from work of Lam. A little higher up on the critical line, our second moment yields a subconvexity bound for the symmetric-square L-function. More specifically, we get subconvexity at
$T^{1/3}$, from work of Lam. A little higher up on the critical line, our second moment yields a subconvexity bound for the symmetric-square L-function. More specifically, we get subconvexity at 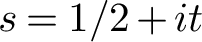 $s=1/2+it$ provided
$s=1/2+it$ provided 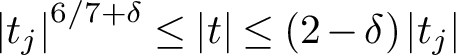 $\left \lvert t_j\right \rvert ^{6/7+\delta }\le \lvert t\rvert \le (2-\delta )\left \lvert t_j\right \rvert $ for any fixed
$\left \lvert t_j\right \rvert ^{6/7+\delta }\le \lvert t\rvert \le (2-\delta )\left \lvert t_j\right \rvert $ for any fixed 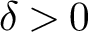 $\delta>0$. Since
$\delta>0$. Since 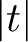 $\lvert t\rvert $ can be taken significantly smaller than
$\lvert t\rvert $ can be taken significantly smaller than 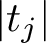 $\left \lvert t_j\right \rvert $, this may be viewed as an approximation to the notorious subconvexity problem for the symmetric-square L-function in the spectral aspect at
$\left \lvert t_j\right \rvert $, this may be viewed as an approximation to the notorious subconvexity problem for the symmetric-square L-function in the spectral aspect at 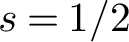 $s=1/2$.
$s=1/2$.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 5 , September 2023 , pp. 2029 - 2073
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by



