Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T06:36:41.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Local quaternionic rigidity for complex hyperbolic lattices

Part of: Lie groups

Published online by Cambridge University Press:  01 September 2010

Inkang Kim ,
Bruno Klingler  and
P. Pansu
Inkang Kim
Affiliation:
School of Mathematics, Korea Institute for Advanced Study, Hoegiro 87, Dongdaemun-gu, Seoul, 130-722, Korea ([email protected])
Bruno Klingler
Affiliation:
Institut de Mathématiques de Jussieu, 175 rue du Chevaleret, 75013 Paris, France ([email protected]) and Institute for Advanced Study, Einstein Drive, Princeton, NJ 08540, USA
P. Pansu
Affiliation:
Laboratoire de Mathématiques d'Orsay, UMR 8628 du CNRS, Université Paris-Sud, 91405 Orsay Cédex, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 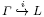be a lattice in the real simple Lie group L. If L is of rank at least 2 (respectively locally isomorphic to Sp(n, 1)) any unbounded morphism ρ : Γ → G into a simple real Lie group G essentially extends to a Lie morphism ρL : L → G (Margulis's superrigidity theorem, respectively Corlette's theorem). In particular any such morphism is infinitesimally, thus locally, rigid. On the other hand, for L = SU(n, 1) even morphisms of the form 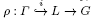are not infinitesimally rigid in general. Almost nothing is known about their local rigidity. In this paper we prove that any cocompact lattice Γ in SU(n, 1) is essentially locally rigid (while in general not infinitesimally rigid) in the quaternionic groups Sp(n, 1), SU(2n, 2) or SO(4n, 4) (for the natural sequence of embeddings SU(n, 1) ⊂ Sp(n, 1) ⊂ SU(2n, 2) ⊂ SO(4n, 4)).

Keywords

rigiditylatticescomplex hyperbolicdeformation

MSC classification

Secondary: 22E40: Discrete subgroups of Lie groups 57S25: Groups acting on specific manifolds
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 11 , Issue 1 , January 2012 , pp. 133 - 159
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Boothby, W. M., Homogeneous complex contact manifolds, Proceedings of Symposia in Pure Mathematics, Volume 3, pp. 144–154 (American Mathematical Society, Providence, RI, 1961).Google Scholar
2.Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups, 2nd edn, Mathematical Surveys and Monographs, Volume 67 (American Mathematical Society, Providence, RI, 2000).Google Scholar
3.Bürger, M. and Iozzi, A., Bounded cohomology and deformation rigidity in complex hyperbolic geometry, preprint (available at http://arxiv.org/pdf/math/0505069).Google Scholar
4.Carlson, J. and Toledo, D., Harmonic mappings of Kähler manifolds to locally symmetric spaces, Publ. Math. IHES 69 (1989), 173–201.CrossRefGoogle Scholar
5.Corlette, K., Flat G-bundles with canonical metrics, J. Diff. Geom. 28 (1988), 361–382.Google Scholar
6.Corlette, K., Rigid representations of Kählerian fundamental groups, J. Diff. Geom. 33(1) (1991), 239–252.Google Scholar
7.Corlette, K., Archimedean superrigidity and hyperbolic geometry, Annals Math. 135 (1992), 165–182.CrossRefGoogle Scholar
8.Goldman, W. M. and Millson, J. J., Local rigidity of discrete groups acting on complex hyperbolic space, Invent. Math. 88 (1987), 495–520.CrossRefGoogle Scholar
9.Goldman, W. M. and Millson, J. J., The deformation theory of representations of fundamental groups of compact Kähler manifolds, Publ. Math. IHES 67 (1988), 43–96.CrossRefGoogle Scholar
10.Gromov, M. and Piatetski-Shapiro, I., Non-arithmetic groups in Lobachevsky spaces, Publ. Math. IHES 65 (1988), 93–103.Google Scholar
11.Gromov, M. and Schoen, R., Harmonic maps into singular spaces and p-adic superrigidity for lattices in groups of rank one, Publ. Math. IHES 76 (1992), 165–246.CrossRefGoogle Scholar
12.Johnson, D. and Millson, J. J., Deformation spaces associated to compact hyperbolic manifolds, in Discrete Groups in Geometry and Analysis, New Haven, CT, 1984, Progress in Mathematics, Volume 67, pp. 48–106 (Birkhäuser, Boston, MA, 1987).Google Scholar
13.Klingler, B., Some remarks on non-Abelian Hodge theory, preprint (available at http://people.math.jussieu.fr/˜klingler/papers.html).Google Scholar
14.Koziarz, V. and Maubon, J., Harmonic maps and representations of non-uniform lattices of PU(m, 1), Annales Inst. Fourier 58(2) (2008), 507–558.CrossRefGoogle Scholar
15.Koziarz, V. and Maubon, J., Representations of complex hyperbolic lattices into rank 2 classical Lie groups of Hermitian type, Geom. Dedicata 137 (2008), 85–111.CrossRefGoogle Scholar
16.Makarov, V. S., On a certain class of discrete subgroups of Lobachevsky space having an infinite fundamental region of finite measure, Sov. Math. Dokl. 7 (1966), 328–331.Google Scholar
17.Margulis, G. A., Discrete subgroups of semisimple Lie groups, Ergebnisse der Mathematik und ihrer Grengebiete, Volume 17 (Springer, 1991).Google Scholar
18.Matsushima, Y. and Murakami, S., On vector bundle valued harmonic forms and automorphic forms on symmetric spaces, Annals Math. 78 (1963), 365–416.CrossRefGoogle Scholar
19.Mostow, G. D., On a remarkable class of polyhedra in complex hyperbolic space, Pac. J. Math. 86 (1980), 171–276.CrossRefGoogle Scholar
20.Raghunathan, M. S., On the first cohomology of discrete subgroups of semi-simple Lie groups, Am. J. Math. 87 (1965), 103–139.CrossRefGoogle Scholar
21.Salamon, S., Quaternionic-Kähler manifolds, Invent. Math. 67(1) (1982), 143–171.CrossRefGoogle Scholar
22.Salamon, S., Quaternion-Kähler geometry, in Surveys in differential geometry: essays on Einstein manifolds, pp. 83–121, Surveys in Differential Geometry, Volume 6 (International Press, Boston, MA, 1999).Google Scholar
23.Selberg, A., On discontinuous groups in higher-dimensional symmetric spaces, in Contributions to Function Theory, Int. Colloq. Function Theory, Bombay, 1960, pp. 147–164 (Tata Institute of Fundamental Research, Bombay, 1960).Google Scholar
24.Simpson, C., Higgs bundles and local systems, Publ. Math. IHES 75 (1992), 5–95.CrossRefGoogle Scholar
25.Vinberg, E. B., Discrete groups generated by reflections in Lobachevsky spaces, Mat. Sb. 1 (1967), 429–444.CrossRefGoogle Scholar
26.Weil, A., Discrete subgroups of Lie groups, II, Annals Math. 75 (1962), 97–123.CrossRefGoogle Scholar
27.Wolf, J., Complex homogeneous contact manifolds and quaternionic symmetric spaces, J. Math. Mech. 14 (1965), 1033–1047.Google Scholar