Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-12T19:41:13.906Z Has data issue: false hasContentIssue false
  • English
  • Français

HECKE ALGEBRAS FOR INNER FORMS OF 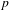$p$-ADIC SPECIAL LINEAR GROUPS

Part of: Lie groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  05 May 2015

Anne-Marie Aubert ,
Paul Baum ,
Roger Plymen  and
Maarten Solleveld
Anne-Marie Aubert
Affiliation:
Institut de Mathématiques de Jussieu – Paris Rive Gauche, U.M.R. 7586 du C.N.R.S., U.P.M.C., 4 place Jussieu 75005 Paris, France ([email protected])
Paul Baum
Affiliation:
Mathematics Department, Pennsylvania State University, University Park, PA 16802, USA ([email protected])
Roger Plymen
Affiliation:
School of Mathematics, Southampton University, Southampton SO17 1BJ, England ([email protected]) School of Mathematics, Manchester University, Manchester M13 9PL, England ([email protected])
Maarten Solleveld
Affiliation:
Radboud Universiteit Nijmegen, Heyendaalseweg 135, 6525AJ Nijmegen, The Netherlands ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $F$ be a non-Archimedean local field, and let 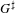$G^{\sharp }$ be the group of $F$-rational points of an inner form of 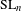$\text{SL}_{n}$. We study Hecke algebras for all Bernstein components of 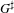$G^{\sharp }$, via restriction from an inner form 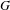$G$ of 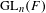$\text{GL}_{n}(F)$.

For any packet of L-indistinguishable Bernstein components, we exhibit an explicit algebra whose module category is equivalent to the associated category of complex smooth 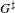$G^{\sharp }$-representations. This algebra comes from an idempotent in the full Hecke algebra of 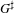$G^{\sharp }$, and the idempotent is derived from a type for 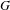$G$. We show that the Hecke algebras for Bernstein components of 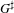$G^{\sharp }$ are similar to affine Hecke algebras of type $A$, yet in many cases are not Morita equivalent to any crossed product of an affine Hecke algebra with a finite group.

Keywords

representation theorydivision algebraHecke algebratypes

MSC classification

Primary: 20G25: Linear algebraic groups over local fields and their integers
Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 2 , April 2017 , pp. 351 - 419
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, J., A note on L-packets, Pure Appl. Math. Q. 2.1 (2006), 199–217.CrossRefGoogle Scholar
Aubert, A.-M., Baum, P. F., Plymen, R. J. and Solleveld, M., The local Langlands correspondence for inner forms of $\text{SL}_{n}$ , Preprint, 2013, arXiv:1305.2638.Google Scholar
Aubert, A.-M., Baum, P. F., Plymen, R. J. and Solleveld, M., On the local Langlands correspondence for non-tempered representations, Münster J. Math. 7 (2014), 27–50.Google Scholar
Bernstein, J. and Deligne, P., Le ‘centre’ de Bernstein, in Représentations des groupes réductifs sur un corps local, pp. 1–32 (Travaux en cours, Hermann, Paris, 1984).Google Scholar
Bushnell, C. J. and Kutzko, P. C., The admissible dual of SL(N) I, Ann. Sci. Éc. Norm. Supér. (4) 26 (1993), 261–280.CrossRefGoogle Scholar
Bushnell, C. J. and Kutzko, P. C., The admissible dual of SL(N) II, Proc. Lond. Math. Soc. (3) 68 (1994), 317–379.CrossRefGoogle Scholar
Bushnell, C. J. and Kutzko, P. C., Smooth representations of reductive p-adic groups: structure theory via types, Proc. Lond. Math. Soc. (3) 77.3 (1998), 582–634.CrossRefGoogle Scholar
Bushnell, C. J. and Kutzko, P. C., Semisimple types in GL n , Compos. Math. 119.1 (1999), 53–97.Google Scholar
Casselman, W., Introduction to the theory of admissible representations of $p$ -adic reductive groups, Preprint, 1995.Google Scholar
Chao, K. F. and Li, W.-W., Dual R-groups of the inner forms of SL(N), Pacific J. Math. 267.1 (2014), 35–90.CrossRefGoogle Scholar
Choiy, K. and Goldberg, D., Transfer of R-groups between p-adic inner forms of SL n , Manus. Math. 146 (2012), 125–152.CrossRefGoogle Scholar
Gelbart, S. S. and Knapp, A. W., L-indistinguishability and R groups for the special linear group, Adv. Math. 43 (1982), 101–121.CrossRefGoogle Scholar
Goldberg, D. and Roche, A., Types in SL n , Proc. Lond. Math. Soc. (3) 85 (2002), 119–138.Google Scholar
Goldberg, D. and Roche, A., Hecke algebras and SL n -types, Proc. Lond. Math. Soc. (3) 90.1 (2005), 87–131.CrossRefGoogle Scholar
Green, J. A., The characters of the finite general linear groups, Trans. Amer. Math. Soc. 80 (1955), 402–447.CrossRefGoogle Scholar
Hiraga, K. and Saito, H., On L-packets for inner forms of SL n , Mem. Amer. Math. Soc. 1013 (2012).Google Scholar
Iwahori, N. and Matsumoto, H., On some Bruhat decomposition and the structure of the Hecke rings of the p-adic Chevalley groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 5–48.CrossRefGoogle Scholar
Lusztig, G., Cells in affine Weyl groups, in Algebraic Groups and Related Topics, Advanced Studies in Pure Mathematics, Volume 6, pp. 255–287 (North Holland, Amsterdam, 1985).CrossRefGoogle Scholar
Meyer, R. and Solleveld, M., The Second Adjointness Theorem for reductive $p$ -adic groups, Preprint, 2010, arXiv:1004.4290.CrossRefGoogle Scholar
Renard, D., Représentations des groupes réductifs p-adiques, Cours spécialisés, Volume 17 (Société Mathématique de France, 2010).Google Scholar
Roche, A., Parabolic induction and the Bernstein decomposition, Compos. Math. 134 (2002), 113–133.CrossRefGoogle Scholar
Sécherre, V., Représentations lisses de GL m (D) III: types simples, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 951–977.CrossRefGoogle Scholar
Sécherre, V. and Stevens, S., Représentations lisses de GL m (D) IV: représentations supercuspidales, J. Inst. Math. Jussieu 7.3 (2008), 527–574.Google Scholar
Sécherre, V. and Stevens, S., Smooth representations of GL(m, D) VI: semisimple types, Int. Math. Res. Not. IMRN (2011).Google Scholar
Silberger, A. J., Introduction to Harmonic Analysis on Reductive p-adic Groups, Mathematical Notes, Volume 23 (Princeton University Press, Princeton NJ, 1979).Google Scholar
Solleveld, M., Periodic cyclic homology of affine Hecke algebras, PhD thesis, Amsterdam (2007) arXiv:0910.1606.Google Scholar
Solleveld, M., Parabolically induced representations of graded Hecke algebras, Algebr. Represent. Theory 15.2 (2012), 233–271.CrossRefGoogle Scholar
Tadić, M., Notes on representations of non-archimedean SL(n), Pacific J. Math. 152.2 (1992), 375–396.CrossRefGoogle Scholar
Waldspurger, J.-L., La formule de Plancherel pour les groupes p-adiques (d’après Harish-Chandra), J. Inst. Math. Jussieu 2.2 (2003), 235–333.CrossRefGoogle Scholar