Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lombardo, Davide
2016.
Explicit surjectivity of Galois representations for abelian surfaces and GL2-varieties.
Journal of Algebra,
Vol. 460,
Issue. ,
p.
26.
NAJMAN, FILIP
2018.
Isogenies of non-CM elliptic curves with rational j-invariants over number fields.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 164,
Issue. 1,
p.
179.
Lozano-Robledo, Álvaro
2018.
Uniform boundedness in terms of ramification.
Research in Number Theory,
Vol. 4,
Issue. 1,
Clark, Pete L.
and
Pollack, Paul
2018.
Pursuing polynomial bounds on torsion.
Israel Journal of Mathematics,
Vol. 227,
Issue. 2,
p.
889.
Parent, Pierre
2018.
Heights on squares of modular curves.
Algebra & Number Theory,
Vol. 12,
Issue. 9,
p.
2065.
Clark, Pete L.
Milosevic, Marko
and
Pollack, Paul
2018.
Typically bounding torsion.
Journal of Number Theory,
Vol. 192,
Issue. ,
p.
150.
Najman, Filip
and
Ţurcaş, George C.
2021.
Irreducibility of mod p Galois representations of elliptic curves with multiplicative reduction over number fields.
International Journal of Number Theory,
Vol. 17,
Issue. 08,
p.
1729.
Genao, Tyler
2022.
Typically bounding torsion on elliptic curves with rational j-invariant.
Journal of Number Theory,
Vol. 238,
Issue. ,
p.
823.
Lombardo, Davide
and
Tronto, Sebastiano
2022.
Some uniform bounds for elliptic curves over
ℚ.
Pacific Journal of Mathematics,
Vol. 320,
Issue. 1,
p.
133.
Banwait, Barinder
Najman, Filip
and
Padurariu, Oana
2023.
Cyclic isogenies of elliptic curves over fixed quadratic fields.
Mathematics of Computation,
Vol. 93,
Issue. 346,
p.
841.
Genao, Tyler
2023.
Typically bounding torsion on elliptic curves isogenous to rational 𝑗-invariant.
Proceedings of the American Mathematical Society,
Banwait, Barinder S
2023.
Explicit Isogenies of Prime Degree Over Quadratic Fields.
International Mathematics Research Notices,
Vol. 2023,
Issue. 14,
p.
11829.
Isik, Erman
Kara, Yasemin
and
Ozman, Ekin
2023.
On ternary Diophantine equations of signature over number fields.
Canadian Journal of Mathematics,
Vol. 75,
Issue. 4,
p.
1293.
Im, Bo-Hae
and
Kim, Hansol
2024.
Growth of torsion groups of elliptic curves over number fields without rationally defined CM.
Journal of Number Theory,
Vol. 258,
Issue. ,
p.
1.
van Bommel, Raymond
Chidambaram, Shiva
Costa, Edgar
and
Kieffer, Jean
2024.
LuCaNT: LMFDB, Computation, and Number Theory.
Vol. 796,
Issue. ,
p.
187.
Banwait, Barinder
Brumer, Armand
Kim, Hyun
Klagsbrun, Zev
Mayle, Jacob
Srinivasan, Padmavathi
and
Vogt, Isabel
2024.
LuCaNT: LMFDB, Computation, and Number Theory.
Vol. 796,
Issue. ,
p.
129.
Lombardo, Davide
and
Verzobio, Matteo
2024.
On the local-global principle for isogenies of abelian surfaces.
Selecta Mathematica,
Vol. 30,
Issue. 2,
Genao, Tyler
2024.
Growth of torsion groups of elliptic curves upon base change from number fields.
The Ramanujan Journal,
Vol. 63,
Issue. 2,
p.
409.
Mayle, Jacob
and
Wang, Tian
2024.
On the effective version of Serre's open image theorem.
Bulletin of the London Mathematical Society,
Vol. 56,
Issue. 4,
p.
1399.
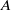 $A$ of dimension
$A$ of dimension  $g$ over a number field
$g$ over a number field 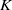 $K$, and a prime
$K$, and a prime 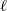 $\ell $, the
$\ell $, the  ${\ell }^{n} $-torsion points of
${\ell }^{n} $-torsion points of 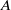 $A$ give rise to a representation
$A$ give rise to a representation 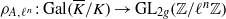 ${\rho }_{A, {\ell }^{n} } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ( \mathbb{Z} / {\ell }^{n} \mathbb{Z} )$. In particular, we get a mod-
${\rho }_{A, {\ell }^{n} } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ( \mathbb{Z} / {\ell }^{n} \mathbb{Z} )$. In particular, we get a mod-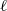 $\ell $representation
$\ell $representation 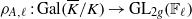 ${\rho }_{A, \ell } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ({ \mathbb{F} }_{\ell } )$ and an
${\rho }_{A, \ell } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ({ \mathbb{F} }_{\ell } )$ and an 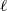 $\ell $-adic representation
$\ell $-adic representation 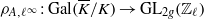 ${\rho }_{A, {\ell }^{\infty } } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ({ \mathbb{Z} }_{\ell } )$. In this paper, we describe the possible determinants of
subquotients of these two representations. These two lists turn out to be remarkably
similar.
${\rho }_{A, {\ell }^{\infty } } : \mathrm{Gal} ( \overline{K} / K)\rightarrow {\mathrm{GL} }_{2g} ({ \mathbb{Z} }_{\ell } )$. In this paper, we describe the possible determinants of
subquotients of these two representations. These two lists turn out to be remarkably
similar.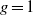 $g= 1$, we recover a generalized version of a theorem of Momose on isogeny
characters of elliptic curves over number fields, and obtain, conditionally on the
Generalized Riemann Hypothesis, a generalization of Mazur’s bound on rational
isogenies of prime degree to number fields.
$g= 1$, we recover a generalized version of a theorem of Momose on isogeny
characters of elliptic curves over number fields, and obtain, conditionally on the
Generalized Riemann Hypothesis, a generalization of Mazur’s bound on rational
isogenies of prime degree to number fields.

