Published online by Cambridge University Press: 06 August 2018
Let  $T$ be a locally finite tree without vertices of degree
$T$ be a locally finite tree without vertices of degree  $1$. We show that among the closed subgroups of
$1$. We show that among the closed subgroups of 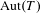 $\text{Aut}(T)$ acting with a bounded number of orbits, the Chabauty-closure of the set of topologically simple groups is the set of groups without proper open subgroup of finite index. Moreover, if all vertices of
$\text{Aut}(T)$ acting with a bounded number of orbits, the Chabauty-closure of the set of topologically simple groups is the set of groups without proper open subgroup of finite index. Moreover, if all vertices of  $T$ have degree
$T$ have degree 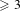 ${\geqslant}3$, then the set of isomorphism classes of topologically simple closed subgroups of
${\geqslant}3$, then the set of isomorphism classes of topologically simple closed subgroups of 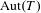 $\text{Aut}(T)$ acting doubly transitively on
$\text{Aut}(T)$ acting doubly transitively on 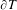 $\unicode[STIX]{x2202}T$ carries a natural compact Hausdorff topology inherited from Chabauty. Some of our considerations are valid in the context of automorphism groups of locally finite connected graphs. Applications to Weyl-transitive automorphism groups of buildings are also presented.
$\unicode[STIX]{x2202}T$ carries a natural compact Hausdorff topology inherited from Chabauty. Some of our considerations are valid in the context of automorphism groups of locally finite connected graphs. Applications to Weyl-transitive automorphism groups of buildings are also presented.
F.R.S.-FNRS Senior Research Associate, supported in part by the ERC (grant no. 278469).
F.R.S.-FNRS Research Fellow.