Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T16:21:10.872Z Has data issue: false hasContentIssue false
  • English
  • Français

BEYOND ENDOSCOPY VIA THE TRACE FORMULA – III THE STANDARD REPRESENTATION

Part of: Discontinuous groups and automorphic forms Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  12 November 2018

S. Ali Altuğ
S. Ali Altuğ*
Affiliation:
MIT, Mathematics, Cambridge, Massachusetts, United States ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We finalize the analysis of the trace formula initiated in S. A. Altuğ [Beyond endoscopy via the trace formula-I: Poisson summation and isolation of special representations, Compos. Math.151(10) (2015), 1791–1820] and developed in S. A. Altuğ [Beyond endoscopy via the trace formula-II: asymptotic expansions of Fourier transforms and bounds toward the Ramanujan conjecture. Submitted, preprint, 2015, Available at: arXiv:1506.08911.pdf], and calculate the asymptotic expansion of the beyond endoscopic averages for the standard $L$-functions attached to weight 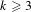$k\geqslant 3$ cusp forms on 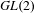$\mathit{GL}(2)$ (cf. Theorem 1.1). This, in particular, constitutes the first example of beyond endoscopy executed via the Arthur–Selberg trace formula, as originally proposed in R. P. Langlands [Beyond endoscopy, in Contributions to Automorphic Forms, Geometry, and Number Theory, pp. 611–698 (The Johns Hopkins University Press, Baltimore, MD, 2004), chapter 22]. As an application we also give a new proof of the analytic continuation of the $L$-function attached to Ramanujan’s 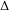$\unicode[STIX]{x1D6E5}$-function.

Keywords

beyond endoscopytrace formula

MSC classification

Primary: 11F11: Holomorphic modular forms of integral weight 11M06: $zeta (s)$ and $L(s, chi)$
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 4 , July 2020 , pp. 1349 - 1387
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altuğ, S. A., Beyond endoscopy via the trace formula-I: Poisson summation and isolation of special representations, Compos. Math. 151(10) (2015), 1791–1820.Google Scholar
Altuğ, S. A., Beyond endoscopy via the trace formula-II: asymptotic expansions of Fourier transforms and bounds towards the Ramanujan conjecture, arXiv:1506.08911.pdf (submitted).Google Scholar
Arthur, J., Problems beyond endoscopy, preprint (2015), available at http://www.math.toronto.edu/arthur/pdf/Arthur.pdf.Google Scholar
Chevalley, C., Théorie Des Groupes De Lie, Groupes algébraiques, Théorèmes généraux sur les algèbes de Lie, Volume 8 (Hermann, Paris, 1968).Google Scholar
Cox, D. A., Primes of the Form x 2 + ny 2 (John Wiley and Sons, Inc., New York, Singapore, Toronto, 1989).Google Scholar
Deligne, P., La conjecture de Weil I (French), Publ. Math. Inst. Hautes Études Sci. 43 (1974), 273–307.Google Scholar
Godement, R. and Jacquet, H., Zeta Functions of Simple Algebras, Lecture Notes in Mathematics, Volume 260 (Springer, Berlin, 1972).Google Scholar
Hecke, E., Mathematische Werke (Vandenhoeck & Ruprecht, Göttingen, 1959).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, Colloquium Publications, Volume 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Knightly, A. and Li., C., Traces of Hecke Operators, Mathematical Surveys and Monographs, Volume 133 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Langlands, R. P., Beyond endoscopy, in Contributions to Automorphic Forms, Geometry, and Number Theory, pp. 611–698 (The Johns Hopkins University Press, Baltimore, MD, 2004), chapter 22.Google Scholar
Sarnak, P., Comments on Robert Langnlands’ lecture: ‘Endoscopy and Beyond (2001), available at http:publications.ias.edu/sites/default/files/SarnakLectureNotes-1.pdf.Google Scholar
Sarnak, P., Nonvanishing of l-functions on ℜ(s) = 1, in Contributions to Automorphic Forms, Geometry, and Number Theory, pp. 719–733 (The Johns Hopkins University Press, Baltimore, MD, 2004), chapter 25.Google Scholar
Selberg, A., Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series, J. Indian Math. Soc. (N.S.) 20 (1956), 47–87.Google Scholar
Serre, J.-P., A Course in Arithmetic, GTM, Volume 7 (Springer, New York, 1996).Google Scholar