No CrossRef data available.
Article contents
On the Books and Forms to be used in Scheduling the Particulars of the Risks of a Life Assurance Company under its Assurance and Annuity Contracts for Periodical or Interim Valuations, Distribution of Surplus, and for Investigation of the Rates of Mortality, Surrender and Lapse
Published online by Cambridge University Press: 18 August 2016
Extract
The method of valuation to be adopted in any office, and the books and forms to be used in scheduling the particulars necessary for it, must be regulated to a great extent by the requirements of “The Life Assurance Companies Act, 1870”; and it will be convenient here to give a brief summary of those requirements so far as they relate to the subject of this essay.
- Type
- Research Article
- Information
- Copyright
- Copyright © Institute and Faculty of Actuaries 1896
References
page 398 note * In writing the reserve value at the end of the year, the symbol V+1 has been used throughout for the sake of clearness, instead of the more correct symbol +1 V.
page 419 note * Since writing the above, it has occurred to me that a better plan would be to insert in the “correction for last payment” column the amount by which the premium payable in the last year falls short of, or exceeds, a full year's premium. The “office yearly premiums” would then be valued as if an integral number of payments were to be received, and the value of the amount of the “correction” deducted, treating it as if it were an endowment. This method would necessitate two multiplications to obtain the value of the premiums, but I think there is little doubt it would be both simpler and more accurate.
page 421 note * I have applied the proposed method of valuation to a number of endowment assurance policies with tontine bonuses maturing at various intervals, taken indiscriminately, in a different office. Altogether, there were 112 policies assuring £23,750, and the sums assured were used in the calculation in the manner described above. The following are the results:
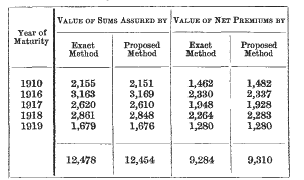
It will be seen that the values agree on the whole very well, both individually and collectively. The total value of the sums assured by the proposed method is less than the total by the exact method by £24 (·19 per-cent),and the total value of the net premiums more by £26 (·28 per-cent). I should mention that, according to the arrangements in force in the particular office referred to, an integral number of payments were to be received in every case at date of valuation. The reserve by the proposed method is £3,144, and by the exact method £3,194, so that the reserve, excluding bonuses, is too little by £50 (·16 percent). The bonuses on these policies were, from various causes, not sufficient to admit of a satisfactory test being applied, and others, therefore, were taken with the following results:
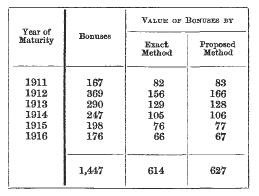
The difference between the totals of the values by the exact and proposed methods is £13 (2·12 per-cent), which is due almost entirely to one year—1912—where there were two or three lives considerably older than the average (see remarks on page 426). The above percentages agree on the whole very well with those given by Mr. Barnes, J.I.A., xxxii, 319.
page 426 note * I have applied the proposed method of valuation of the premiums to the limited payment policies in a different office, and found the results confirm the previous calculation. The durations were taken indiscriminately ; and the net premiums were used because the exact values of them had already been computed. Altogether there were 133 policies, and the results are given in the following table:
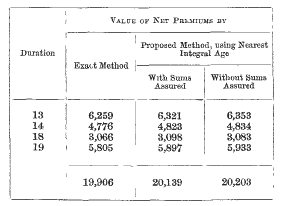
It will be observed that here also the values by the proposed method are in every case greater than the exact values, although the difference on the whole is small, being 1·18 per-cent of the exact values, when the sums assured are used, as against 1·53 in the previous calculation. This, of course, is due to the inclusion of lives considerably above the average. After age 45 the annuity-value for the same duration rapidly decreases, and the inclusion of a few lives above that age does not increase the average age of the group sufficiently to make a material difference in the annuity-value. There were ten policies on lives over 45 in the above calculation, and the amount of the error due to them, when the sums assured are used, is £174. I should add that an integral number of payments were to be received in every case at date of valuation.
page 442 note * I estimate from the returns of some of the largest offices that the number of such policies would rarely exceed 300, while in most cases it would be very much less. The large majority of them are joint life and contingent policies, the reserve-values of which are readily calculated.


