Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-04T09:41:21.612Z Has data issue: false hasContentIssue false
  • English
  • Français

A general theory of mortality

Published online by Cambridge University Press:  18 August 2016

C. D. Rich
C. D. Rich
Affiliation:
Provident Mutual Life Assurance Association
Get access Rights & Permissions [Opens in a new window]

Extract

If a pebble on a steep hill is disturbed from a state of rest, it will probably roll down the hill gathering speed as it goes, and, if the hill ends in a precipice, the pebble will, unless it is checked in its course, eventually fall over the edge. So long as the pebble is rolling down the hill it is within sight of an observer on the hill, but when it falls over the precipice it passes out of his sight; its disappearance occurs suddenly. There is no violent change in the pebble's speed or direction as it passes over the edge, so the suddenness of its disappearance is not due to any alteration in its motion but to the fact that it has rolled down beyond the level of the edge of the hill.

Type
Research Article
Information
Journal of the Institute of Actuaries , Volume 70 , Issue 3 , April 1940 , pp. 314 - 379
Copyright
Copyright © Institute and Faculty of Actuaries 1939

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 352 note * Strictly speaking, it has also been assumed that the functions are differentiable. It is taken for granted here and elsewhere in the Appendix that the functions dealt with are reasonably “well-behaved “. Reference will not therefore be made to matters, such as uniform continuity, which might from a rigorous mathematical standpoint require consideration.

page 353 note * To arrive at the solution from (3), let 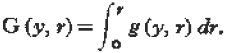Integrating (3) with respect to r between the limits 0 and r,

To satisfy this equation, it can be seen that G (y, r) must be a function of re −λy , and in order that it may take the required form when y is put equal to o it must be G (o, re −λy ). Hence, differentiating with respect to r, we obtain the solution for g (y, r).