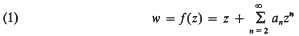Research Article
One-relator groups that are residually of prime power order
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-409
-
- Article
-
- You have access
- Export citation
Maximal right ideals of transformation near-rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 410-412
-
- Article
-
- You have access
- Export citation
Some results concerning a transformation semigroup
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-425
-
- Article
-
- You have access
- Export citation
Minimal arcs in metric spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 426-430
-
- Article
-
- You have access
- Export citation
Ordering finite groups by involvement
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 431-436
-
- Article
-
- You have access
- Export citation
A class of modules over a locally finite group II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 437-469
-
- Article
-
- You have access
- Export citation
Generalised partial transformation semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 470-473
-
- Article
-
- You have access
- Export citation
Filters and overrings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 474-480
-
- Article
-
- You have access
- Export citation
Nonlinear symmetric bending of circular elastic plates
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-504
-
- Article
-
- You have access
- Export citation
Star center points of starlike functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 505-510
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 19 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 19 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation