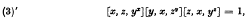Research Article
Forced motion of a charged particle in a magnetic field
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-398
-
- Article
-
- You have access
- Export citation
A note on a result of Mahler's
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 399-401
-
- Article
-
- You have access
- Export citation
On Rotor calculus, I
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 402-423
-
- Article
-
- You have access
- Export citation
On Rotor calculus, II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 424-448
-
- Article
-
- You have access
- Export citation
A note on doubly transitive groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 449-451
-
- Article
-
- You have access
- Export citation
Rational polygons
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 452-459
-
- Article
-
- You have access
- Export citation
Generalization of a theorem of P. D. Finch's on integration of set-functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 460-465
-
- Article
-
- You have access
- Export citation
Finite simple groups with nilpotent third maximal subgroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 466-469
-
- Article
-
- You have access
- Export citation
Summation of infinite series
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 470-476
-
- Article
-
- You have access
- Export citation
A converse to Lebesgue's dominated convergence theorem
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 477-479
-
- Article
-
- You have access
- Export citation
Involutory automorphisms of groups of odd order
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 480-494
-
- Article
-
- You have access
- Export citation
On the lattice equivalence of topological spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 495-511
-
- Article
-
- You have access
- Export citation
Corrigendum
Another Law for the 3-Metabelian Groups
-
- Published online by Cambridge University Press:
- 09 April 2009, p. 512
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 6 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 6 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation


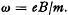 .
.
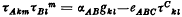
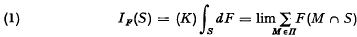
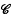 of its subsets which has the properties (i) arbitrary set intersections of members of
of its subsets which has the properties (i) arbitrary set intersections of members of 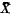 denotes the closure of
denotes the closure of 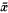 . The pair (
. The pair (