Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-27T18:19:09.486Z Has data issue: false hasContentIssue false
  • English
  • Français

WEIGHTED ORLICZ ALGEBRAS ON LOCALLY COMPACT GROUPS

Part of: Linear function spaces and their duals Abstract harmonic analysis Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  02 September 2015

ALEN OSANÇLIOL  and
SERAP ÖZTOP
ALEN OSANÇLIOL
Affiliation:
Department of Mathematics, Faculty of Science, İstanbul University, İstanbul, Turkey email [email protected]
SERAP ÖZTOP*
Affiliation:
Department of Mathematics, Faculty of Science, İstanbul University, İstanbul, Turkey email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

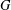For a locally compact group $G$ with left Haar measure and a Young function 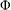${\rm\Phi}$, we define and study the weighted Orlicz algebra 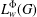$L_{w}^{{\rm\Phi}}(G)$ with respect to convolution. We show that 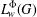$L_{w}^{{\rm\Phi}}(G)$ admits no bounded approximate identity under certain conditions. We prove that a closed linear subspace 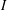$I$ of the algebra 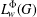$L_{w}^{{\rm\Phi}}(G)$ is an ideal in 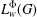$L_{w}^{{\rm\Phi}}(G)$ if and only if 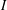$I$ is left translation invariant. For an abelian 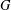$G$, we describe the spectrum (maximal ideal space) of the weighted Orlicz algebra and show that weighted Orlicz algebras are semisimple.

Keywords

weighted Orlicz spaceYoung functionunbounded approximate identitymaximal ideal spacesemisimple

MSC classification

Primary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Secondary: 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc. 46J20: Ideals, maximal ideals, boundaries
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 3 , December 2015 , pp. 399 - 414
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Akbarbaglu, I. and Maghsoudi, S., ‘Banach–Orlicz algebras on a locally compact group’, Mediterr. J. Math. 10 (2013), 1937–1947.CrossRefGoogle Scholar
Bharucha, P., ‘Amenability properties and their consequences in Banach algebras’, PhD Thesis, Australian National University, 2008.Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis II (Springer, New York, 1997).Google Scholar
Hudzik, H., Kamińska, A. and Musielak, J., ‘On some Banach algebras given by a modular’, in: Alfred Haar Memorial Conference, Budapest, Colloquia Mathematica Societatis János Bolyai, 49 (North-Holland, Amsterdam, 1987), 445–463.Google Scholar
Kaniuth, E., A Course in Commutative Banach Algebras (Springer, New York, 2009).CrossRefGoogle Scholar
Krasnosel’skii, M. A. and Rutickii, Ja. B., Convex Functions and Orlicz Spaces (Noordhoff, Groningen, 1961).Google Scholar
Kuznetsova, Yu. N., ‘Weighted L p -Algebras on Groups’, Funct. Anal. Appl. 40(3) (2006), 234–236; (English transl.).CrossRefGoogle Scholar
Kuznetsova, Yu. N., ‘Invariant weighted algebras’, Mat. Zametki 84(4) (2008), 567–576.Google Scholar
Rao, M. M. and Ren, Z. D., Theory of Orlicz Spaces (Marcel Dekker, New York, 1991).Google Scholar
Reiter, H. and Stegeman, J. D., Classical Harmonic Analysis and Locally Compact Groups (Clarendon Press, Oxford, 2000).CrossRefGoogle Scholar
Saeki, S., ‘The L p -conjecture and Young’s inequality’, Illinois J. Math. 34(3) (1990), 614–627.CrossRefGoogle Scholar