Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T07:26:17.099Z Has data issue: false hasContentIssue false
  • English
  • Français

WEIGHTED ESTIMATES FOR SINGULAR INTEGRAL OPERATORS WITH NONSMOOTH KERNELS AND APPLICATIONS

Part of: Harmonic analysis in several variables Abstract harmonic analysis General theory of linear operators

Published online by Cambridge University Press:  01 December 2008

GUOEN HU  and
DACHUN YANG
GUOEN HU
Affiliation:
Department of Applied Mathematics, University of Information Engineering, P.O. Box 1001-747, Zhengzhou 450002, People’s Republic of China (email: [email protected])
DACHUN YANG*
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s Republic of China (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

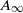Let 𝒳 be a space of homogeneous type in the sense of Coifman and Weiss. In this paper, two weighted estimates related to weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted Lp(𝒳) and weighted endpoint estimates with general weights are obtained for singular integral operators with nonsmooth kernels, their commutators with BMO (𝒳) functions, and associated maximal operators. Some applications to holomorphic functional calculi of elliptic operators and Schrödinger operators are also presented.

Keywords

space of homogeneous typeapproximation to the identityweightnorm inequalitysingular integral operatormaximal operatornonsmooth kernel

MSC classification

Secondary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.) 42B25: Maximal functions, Littlewood-Paley theory 47A30: Norms (inequalities, more than one norm, etc.) 43A99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 85 , Issue 3 , December 2008 , pp. 377 - 417
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

The first author was supported by the NNSF (No. 10671210) of China and the second (corresponding) author was supported by National Science Foundation for Distinguished Young Scholars (No. 10425106) and NCET (No. 04-0142) of China.

References

[1]Amiar, H., ‘Singular integrals and approximate identities on spaces of homogeneous type’, Trans. Amer. Math. Soc. 292 (1985), 135–153.Google Scholar
[2]Amiar, H., ‘Rearrangement and continuity properties of BMO (ϕ) functions on spaces of homogeneous type’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 18 (1991), 353–362.Google Scholar
[3]Coifman, R. R. and Weiss, G., Analyse harmonique non-commutative sur certain espaces homogènes, Lecture notes in Mathematics, 242 (Springer, Berlin, 1971).CrossRefGoogle Scholar
[4]Duong, X. T. and McIntosh, A., ‘Singular integral operators with nonsmooth kernels on irregular domains’, Rev. Mat. Iberoamericana 15 (1999), 233–265.CrossRefGoogle Scholar
[5]Duong, X. T. and Yan, L., ‘Commutators of BMO functions and singular integral operators with nonsmooth kernels’, Bull. Austral. Math. Soc. 67 (2003), 187–200.CrossRefGoogle Scholar
[6]Duong, X. T. and Yan, L., ‘New function spaces of BMO type, the John–Nirenberg inequality, interpolation, and applications’, Commun. Pure Appl. Math. 58 (2005), 1375–1420.CrossRefGoogle Scholar
[7]García-Cuerva, L. and Rubio de Francia, J. L., Weighted Norm Inequalities and Related Topics, North-Holland Mathematics Studies, 116 (North-Holland, Amsterdam, 1985).Google Scholar
[8]Macías, R. and Segovia, C., ‘Lipschitz functions on spaces of homogeneous type’, Adv. Math. 33 (1979), 257–270.Google Scholar
[9]Martell, J. M., ‘Sharp maximal functions associated with approximations of the identity in spaces of homogeneous type and applications’, Studia Math. 161 (2004), 113–145.CrossRefGoogle Scholar
[10]Pérez, C., ‘Weighted norm inequalities for singular integral operators’, J. London Math. Soc. (2) 49 (1994), 296–308.Google Scholar
[11]Pérez, C., ‘Endpoint estimates for commutators of singular integral operators’, J. Funct. Anal. 128 (1995), 163–185.CrossRefGoogle Scholar
[12]Pérez, C., ‘On sufficient conditions for the boundedness of the Hardy–Littlewood maximal operator between weighted L p-spaces with different weights’, Proc. London Math. Soc. (3) 71 (1995), 135–157.CrossRefGoogle Scholar
[13]Pérez, C., ‘Sharp estimates for commutators of singular integrals via iterations of the Hardy–Littlewood maximal function’, J. Fourier Anal. Appl. 3 (1997), 743–756.Google Scholar
[14]Pérez, C. and Pradolini, G., ‘Sharp weighted endpoint estimates for commutators of singular integrals’, Michigan Math. J. 49 (2001), 23–37.Google Scholar
[15]Pérez, C. and Wheeden, R. L., ‘Uncertainty principle estimates for vector fields’, J. Funct. Anal. 181 (2001), 146–188.CrossRefGoogle Scholar
[16]Pradolini, G. and Salinas, O., ‘Commutators of singular integrals on spaces of homogeneous type’, Czech. Math. J. 57(132) (2007), 75–93.CrossRefGoogle Scholar
[17]Rao, M. M. and Ren, Z. D., Theory of Orlicz Spaces (Marcel Dekker, New York, 1991).Google Scholar
[18]Rivière, N. M., ‘Singular integrals and multiplier operators’, Ark. Mat. 9 (1971), 243–278.CrossRefGoogle Scholar
[19]Stein, E. M., ‘Note on the class Llog L’, Studia Math. 32 (1969), 305–310.CrossRefGoogle Scholar
[20]Strömberg, J. O. and Torchinsky, A., Weighted Hardy Spaces, Lecture Notes in Mathematics, 1381 (Springer, Berlin, 1989).CrossRefGoogle Scholar