Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T05:28:11.633Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAK-STAR PROPERTIES OF HOMOMORPHISMS FROM WEIGHTED CONVOLUTION ALGEBRAS ON THE HALF-LINE

Part of: Special classes of linear operators Linear function spaces and their duals Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  20 July 2010

THOMAS VILS PEDERSEN
THOMAS VILS PEDERSEN*
Affiliation:
Department of Natural Sciences and Environment, Faculty of Life Sciences, University of Copenhagen, Thorvaldsensvej 40, DK-1871 Frederiksberg C, Denmark (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L1(ω) be the weighted convolution algebra L1ω(ℝ+) on ℝ+ with weight ω. Grabiner recently proved that, for a nonzero, continuous homomorphism Φ:L1(ω1)→L1(ω2), the unique continuous extension 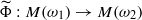to a homomorphism between the corresponding weighted measure algebras on ℝ+ is also continuous with respect to the weak-star topologies on these algebras. In this paper we investigate whether similar results hold for homomorphisms from L1(ω) into other commutative Banach algebras. In particular, we prove that for the disc algebra 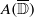every nonzero homomorphism 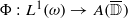extends uniquely to a continuous homomorphism 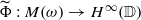which is also continuous with respect to the weak-star topologies. Similarly, for a large class of Beurling algebras A+v on 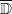(including the algebra of absolutely convergent Taylor series on 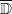) we prove that every nonzero homomorphism Φ:L1(ω)→A+v extends uniquely to a continuous homomorphism 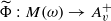which is also continuous with respect to the weak-star topologies.

Keywords

homomorphismsweighted convolution algebrasweak-star continuityfunction algebras

MSC classification

Secondary: 46J10: Banach algebras of continuous functions, function algebras 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 47B38: Operators on function spaces (general)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 89 , Issue 1 , August 2010 , pp. 75 - 90
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Dales, H. G., Banach Algebras and Automatic Continuity, London Mathematical Society Monographs, New Series, 24 (Oxford University Press, Oxford, 2000).Google Scholar
[2]Esterle, J., ‘Quasimultipliers, representations of H ∞, and the closed ideal problem for commutative Banach algebras’, in: Radical Banach Algebras and Automatic Continuity, Lecture Notes in Mathematics, 975 (eds. Bachar, J. M.et al.) (Springer, Berlin, 1983), pp. 66–162.Google Scholar
[3]Ghahramani, F., McClure, J. P. and Grabiner, S., ‘Standard homomorphisms and regulated weights on weighted convolution algebras’, J. Funct. Anal. 91 (1990), 278–286.Google Scholar
[4]Grabiner, S., ‘Homomorphisms and semigroups in weighted convolution algebras’, Indiana Univ. Math. J. 37 (1988), 589–615.CrossRefGoogle Scholar
[5]Grabiner, S., ‘Weak * properties of weighted convolution algebras II’, Preprint, 2006.Google Scholar
[6]Hille, E. and Phillips, R. S., Functional Analysis and Semi-Groups, American Mathematical Society Colloquium Publications, 31 (American Mathematical Society, Providence, RI, 1957), revised edition.Google Scholar
[7]Hoffman, K., Banach Spaces of Analytic Functions (Prentice Hall, Englewood Cliffs, NJ, 1962).Google Scholar
[8]Pedersen, T. V., ‘Sinclair homomorphisms and semigroups of analytic functions’, J. Funct. Anal. 145 (1997), 527–554.Google Scholar
[9]Pedersen, T. V., ‘Banach algebras weak * generated by their idempotents’, Proc. Edinb. Math. Soc. 45 (2002), 681–692.Google Scholar
[10]Rudin, W., Real and Complex Analysis, 3rd edn (McGraw-Hill, New York, 1987).Google Scholar
[11]Sinclair, A. M., Continuous Semigroups in Banach Algebras, London Mathematical Society Lecture Note Series, 63 (Cambridge University Press, Cambridge, 1982).Google Scholar