Hostname: page-component-7479d7b7d-jwnkl Total loading time: 0 Render date: 2024-07-09T01:41:40.406Z Has data issue: false hasContentIssue false
  • English
  • Français

A VON NEUMANN ALGEBRA CHARACTERIZATION OF PROPERTY (T) FOR GROUPOIDS

Part of: Selfadjoint operator algebras Ergodic theory Groupoids

Published online by Cambridge University Press:  21 December 2018

MARTINO LUPINI Open the ORCID record for MARTINO LUPINI [Opens in a new window]
MARTINO LUPINI*
Affiliation:
Victoria University of Wellington, School of Mathematics & Statistics, PO Box 600, 6140Wellington, New Zealand email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For an arbitrary discrete probability-measure-preserving groupoid 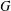$G$, we provide a characterization of property (T) for $G$ in terms of the groupoid von Neumann algebra 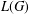$L(G)$. More generally, we obtain a characterization of relative property (T) for a subgroupoid 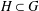$H\subset G$ in terms of the inclusions 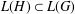$L(H)\subset L(G)$.

Keywords

groupoidvon Neumann algebraproperty (T)Kazhdan groupoidbimodulecohomologyrepresentation

MSC classification

Primary: 20L05: Groupoids (i.e. small categories in which all morphisms are isomorphisms)
Secondary: 46L10: General theory of von Neumann algebras 37A15: General groups of measure-preserving transformations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 3 , June 2020 , pp. 363 - 386
Copyright
© 2018 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by the NSF Grant DMS-1600186.

References

Aaserud, A., ‘Applications of property (T) for groups and von Neumann algebras’, PhD Thesis, University of Copenhagen, 2011.Google Scholar
Anantharaman-Delaroche, C., ‘Cohomology of property (T) groupoids and applications’, Ergod. Th. & Dynam. Sys. 25(4) (2005), 977–1013.Google Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan’s Property (T), New Mathematical Monographs, 11 (Cambridge University Press, Cambridge, 2008).Google Scholar
Blackadar, B., Operator Algebras, Encyclopaedia of Mathematical Sciences, 122 (Springer, Berlin, 2006).Google Scholar
Connes, A. and Jones, V., ‘Property T for von Neumann algebras’, Bull. Lond. Math. Soc. 17(1) (1985), 57–62.Google Scholar
Gardella, E. and Lupini, M., ‘Representations of étale groupoids on L p-spaces’, Adv. Math. 318 (2017), 233–278.Google Scholar
Gardella, E. and Lupini, M., ‘The complexity of conjugacy, orbit equivalence, and von Neumann equivalence of actions of nonamenable groups’, Preprint, 2017, arXiv:1708.01327.Google Scholar
Haagerup, U., ‘An example of a nonnuclear C*-algebra, which has the metric approximation property’, Invent. Math. 50(3) (1978), 279–293.Google Scholar
de la Harpe, P. and Valette, A., ‘La propriété (T) de Kazhdan pour les groupes localement compacts (avec un appendice de Marc Burger)’, Astérisque 175 (1989), 158 pages.Google Scholar
Ioana, A., Peterson, J. and Popa, S., ‘Amalgamated free products of weakly rigid factors and calculation of their symmetry groups’, Acta Math. 200(1) (2008), 85–153.Google Scholar
Jolissaint, P., ‘On property (T) for pairs of topological groups’, L’Enseignement Mathématique 51(1–2) (2005), 31–45.Google Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras. Vol. II, Pure and Applied Mathematics, 100 (Academic Press, Orlando, FL, 1986).Google Scholar
Kechris, A., Classical Descriptive Set Theory, Graduate Texts in Mathematics, 156 (Springer, New York, 1995).Google Scholar
Moore, C. C., ‘Ergodic theory and von Neumann algebras’, in: Operator Algebras and Applications, Part 2 (Kingston, Ont. 1980), Proceedings of Symposia in Pure Mathematics, 38 (American Mathematical Society, Providence, RI, 1982), 179–226.Google Scholar
Peterson, J., ‘A 1-cohomology characterization of property (T) in von Neumann algebras’, Pacific J. Math. 243(1) (2009), 181–199.Google Scholar
Peterson, J. and Popa, S., ‘On the notion of relative property (T) for inclusions of von Neumann algebras’, J. Funct. Anal. 219(2) (2005), 469–483.Google Scholar
Popa, S., ‘Correspondences’, INCREST preprint (1986) unpublished.Google Scholar
Popa, S., ‘On a class of type II1 factors with Betti numbers invariants’, Ann. of Math. (2) 163(3) (2006), 809–899.Google Scholar
Ramsay, A., ‘Virtual groups and group actions’, Adv. Math. 6(3) (1971), 253–322.Google Scholar
Renault, J., C*-algebras and Dynamical Systems, Publicações Matemáticas do IMPA (Instituto Nacional de Matemética Pura e Aplicada, Rio de Janeiro, 2009).Google Scholar
Takesaki, M., Theory of Operator Algebras. I, Encyclopaedia of Mathematical Sciences, 124 (Springer, Berlin, 2002).Google Scholar
Williams, D. P., Crossed Products of C*-algebras, Mathematical Surveys and Monographs, 134 (American Mathematical Society, Providence, RI, 2007).Google Scholar
Zimmer, R. J., ‘On the cohomology of ergodic actions of semisimple Lie groups and discrete subgroups’, Amer. J. Math. 103(5) (1981), 937–951.Google Scholar