Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kovács, L. G.
1969.
A Remark on Critical Groups.
Journal of the Australian Mathematical Society,
Vol. 9,
Issue. 3-4,
p.
465.
Plotkin, B. I.
1973.
General theory of groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 5,
p.
527.
Woeppel, James J.
1977.
Critical groups having central monoliths of a nilpotent by abelian product variety of groups.
Transactions of the American Mathematical Society,
Vol. 225,
Issue. 0,
p.
155.
Mikaelian, V. H.
2015.
Varieties Generated by Wreath Products of Abelian and Nilpotent Groups.
Algebra and Logic,
Vol. 54,
Issue. 1,
p.
70.
Mikaelian, V. H.
2017.
The Criterion of Shmel’kin and Varieties Generated by Wreath Products of Finite Groups.
Algebra and Logic,
Vol. 56,
Issue. 2,
p.
108.
Mikaelian, Vahagn H.
2018.
Subvariety structures in certain product varieties of groups.
Journal of Group Theory,
Vol. 21,
Issue. 5,
p.
865.
Mikaelian, V. H.
2018.
Kp-series and varieties generated by wreath products of p-groups.
International Journal of Algebra and Computation,
Vol. 28,
Issue. 08,
p.
1693.
Mikaelian, V. H.
2018.
On the classification of varieties generated by wreath products of groups.
Izvestiya: Mathematics,
Vol. 82,
Issue. 5,
p.
1006.
Mikaelian, Vahagn H.
2018.
О классификации многообразий, порожденных сплетениями групп.
Известия Российской академии наук. Серия математическая,
Vol. 82,
Issue. 5,
p.
153.


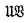 is generated by a finite group if and only if
is generated by a finite group if and only if 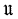 is nilpotent,
is nilpotent, 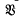 is abelian, and the exponents of
is abelian, and the exponents of 