Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T15:18:55.871Z Has data issue: false hasContentIssue false
  • English
  • Français

A VARIATIONAL APPROACH FOR ONE-DIMENSIONAL PRESCRIBED MEAN CURVATURE PROBLEMS

Part of: Manifolds Boundary value problems

Published online by Cambridge University Press:  25 July 2014

GHASEM A. AFROUZI ,
ARMIN HADJIAN  and
GIOVANNI MOLICA BISCI
GHASEM A. AFROUZI
Affiliation:
Department of Mathematics, Faculty of Mathematical Sciences, University of Mazandaran, Babolsar, Iran email [email protected]
ARMIN HADJIAN
Affiliation:
Department of Mathematics, Faculty of Basic Sciences, University of Bojnord, PO Box 1339, Bojnord 94531, Iran email [email protected]
GIOVANNI MOLICA BISCI*
Affiliation:
Dipartimento P.A.U., Università degli Studi “Mediterranea”, di Reggio Calabria - Feo di Vito, 89124 Reggio Calabria, Italy email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We discuss the multiplicity of nonnegative solutions of a parametric one-dimensional mean curvature problem. Our main effort here is to describe the configuration of the limits of a certain function, depending on the potential at zero, that yield, for certain values of the parameter, the existence of infinitely many weak nonnegative and nontrivial solutions. Moreover, thanks to a classical regularity result due to Lieberman, this sequence of solutions strongly converges to zero in 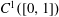$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1([0,1])$. Our approach is based on recent variational methods.

Keywords

one-dimensional prescribed curvature problemvariational methodsinfinitely many solutions

MSC classification

Secondary: 34B15: Nonlinear boundary value problems 49Q20: Variational problems in a geometric measure-theoretic setting
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 2 , October 2014 , pp. 145 - 161
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Afrouzi, G. A. and Hadjian, A., ‘Infinitely many solutions for a class of Dirichlet quasilinear elliptic systems’, J. Math. Anal. Appl. 393 (2012), 265–272.Google Scholar
Afrouzi, G. A., Hadjian, A. and Heidarkhani, S., ‘Infinitely many solutions for a mixed doubly eigenvalue boundary value problem’, Mediterr. J. Math. 10 (2013), 1317–1331.CrossRefGoogle Scholar
Afrouzi, G. A., Hadjian, A. and Molica Bisci, G., ‘Some remarks for one-dimensional mean curvature problems through a local minimization principle’, Adv. Nonlinear Anal. 2 (2013), 427–441.Google Scholar
Bartnik, R. and Simon, L., ‘Spacelike hypersurfaces with prescribed boundary values and mean curvature’, Comm. Math. Phys. 87 (1982), 131–152.Google Scholar
Bereanu, C. and Mawhin, J., ‘Boundary-value problems with non-surjective ϕ-Laplacian and one-sided bounded nonlinearity’, Adv. Differential Equations 11 (2006), 35–60.Google Scholar
Bonheure, D., Habets, P., Obersnel, F. and Omari, P., ‘Classical and non-classical solutions of a prescribed curvature equation’, J. Differential Equations 243 (2007), 208–237.Google Scholar
Bonheure, D., Habets, P., Obersnel, F. and Omari, P., ‘Classical and non-classical positive solutions of a prescribed curvature equation with singularities’, Rend. Istit. Mat. Univ. Trieste 39 (2007), 63–85.Google Scholar
Capietto, A., Dambrosio, W. and Zanolin, F., ‘Infinitely many radial solutions to a boundary value problem in a ball’, Ann. Mat. Pure Appl. 179 (2001), 159–188.Google Scholar
Chang, K.-C. and Zhang, T., ‘Multiple solutions of the prescribed mean curvature equation’, in: Nankai Tracts Math., Inspired by S. S. Chern, 11 (ed. Griffiths, P. A.) (World Scientific Publications, Hackensack, NJ, 2006), 113–127.Google Scholar
Coelho, I., Corsato, C., Obersnel, F. and Omari, P., ‘Positive solutions of the Dirichlet problem for the one-dimensional Minkowski-curvature equation’, Adv. Nonlinear Stud. 12 (2012), 621–638.Google Scholar
Degiovanni, M., Marzocchi, M. and Rădulescu, V. D., ‘Multiple solutions of hemivariational inequalities with area-type term’, Calc. Var. Partial Differential Equations 10 (2000), 355–387.Google Scholar
Faraci, F., ‘A note on the existence of infinitely many solutions for the one dimensional prescribed curvature equation’, Stud. Univ. Babeş–Bolyai Math. 55 (2010), 83–90.Google Scholar
Habets, P. and Omari, P., ‘Positive solutions of an indefinite prescribed mean curvature problem on a general domain’, Adv. Nonlinear Stud. 4 (2004), 1–13.Google Scholar
Habets, P. and Omari, P., ‘Multiple positive solutions of a one-dimensional prescribed mean curvature problem’, Comm. Contemp. Math. 9 (2007), 701–730.Google Scholar
Kristály, A., Rădulescu, V. and Varga, Cs., Variational Principles in Mathematical Physics, Geometry, and Economics: Qualitative Analysis of Nonlinear Equations and Unilateral Problems, Encyclopedia of Mathematics and its Applications, 136 (Cambridge University Press, Cambridge, 2010).Google Scholar
Le, V. K., ‘Some existence results on non-trivial solutions of the prescribed mean curvature equation’, Adv. Nonlinear Stud. 5 (2005), 133–161.Google Scholar
Le, V. K., ‘A Ljusternik–Schnirelmann type theorem for eigenvalues of a prescribed mean curvature problem’, Nonlinear Anal. 64 (2006), 1503–1527.Google Scholar
Lieberman, G. M., ‘Boundary regularity for solutions of degenerate elliptic equations’, Nonlinear Anal. 12 (1988), 1203–1219.Google Scholar
Marzocchi, M., ‘Multiple solutions of quasilinear equations involving an area-type term’, J. Math. Anal. Appl. 196 (1995), 1093–1104.Google Scholar
Marzocchi, M., ‘Nontrivial solutions of quasilinear equations in BV’, Serdica Math. J. 22 (1996), 451–470.Google Scholar
Molica Bisci, G., ‘Variational problems on the sphere’, in: Recent Trends in Nonlinear Partial Differential Equations, Dedicated to Patrizia Pucci on the occasion of her 60th birthday, Contemporary Mathematics, 595 (eds. Serrin, J., Mitidieri, E. and Rădulescu, V.) (American Mathematical Society, 2013), 273–291.Google Scholar
Ni, W. M. and Serrin, J., ‘Non-existence theorems for quasilinear partial differential equations’, Rend. Circ. Mat. Palermo (2) Suppl. 8 (1985), 171–185.Google Scholar
Ni, W. M. and Serrin, J., ‘Existence and non-existence theorems for ground states of quasilinear partial differential equations. The anomalous case’, Atti Convegni Lincei 77 (1986), 231–257.Google Scholar
Ni, W. M. and Serrin, J., ‘Non-existence theorems for singular solutions of quasilinear partial differential equations’, Comm. Pure Appl. Math. 39 (1986), 379–399.Google Scholar
Obersnel, F., ‘Classical and non-classical sign-changing solutions of a one-dimensional autonomous prescribed curvature equation’, Adv. Nonlinear Stud. 7 (2007), 671–682.Google Scholar
Obersnel, F. and Omari, P., ‘Existence and multiplicity results for the prescribed mean curvature equation via lower and upper solutions’, Differential Integral Equations 22 (2009), 853–880.Google Scholar
Obersnel, F. and Omari, P., ‘Positive solutions of the Dirichlet problem for the prescribed mean curvature equation’, J. Differential Equations 249 (2010), 1674–1725.Google Scholar
Obersnel, F. and Omari, P., ‘Multiple non-trivial solutions of the Dirichlet problem for the prescribed mean curvature equation’, in: Nonlinear Elliptic Partial Differential Equations, Contemporary Mathematics, 540 (American Mathematical Society, Providence, RI, 2011), 165–185.Google Scholar
Pan, H., ‘One-dimensional prescribed mean curvature equation with exponential nonlinearity’, Nonlinear Anal. 70 (2009), 999–1010.Google Scholar
Peletier, L. A. and Serrin, J., ‘Ground states for the prescribed mean curvature equation’, Proc. Amer. Math. Soc. 100 (1987), 694–700.Google Scholar
Pisano, A. and Fuschi, P., ‘Closed form solution for a nonlocal elastic bar in tension’, Intl. J. Solids Struct. 40 (2003), 13–23.Google Scholar
Polizzotto, C., Fuschi, P. and Pisano, A., ‘A nonhomogeneous nonlocal elasticity model’, Eur. J. Mech. A Solids 25 (2006), 308–333.Google Scholar
Ricceri, B., ‘A general variational principle and some of its applications’, J. Comput. Appl. Math. 113 (2000), 401–410.Google Scholar
Tolksdorf, P., ‘On the Dirichlet problem for quasilinear equations in domains with conical boundary points’, Comm. Partial Differential Equations 8 (1983), 773–817.CrossRefGoogle Scholar