USING IDEALS TO PROVIDE A UNIFIED APPROACH TO UNIQUELY CLEAN RINGS

Abstract

In this article, we introduce the notion of the uniquely 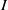$I$-clean ring and show that, if 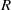$R$ is a ring and 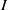$I$ is an ideal of 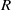$R$ then 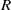$R$ is uniquely 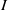$I$-clean if and only if (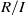$R/ I$ is Boolean and idempotents lift uniquely modulo 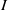$I$) if and only if (for each 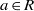$a\in R$ there exists a central idempotent 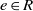$e\in R$ such that 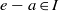$e- a\in I$ and 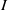$I$ is idempotent-free). We examine when ideal extension is uniquely clean relative to an ideal. Also we obtain conditions on a ring 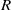$R$ and an ideal 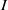$I$ of 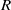$R$ under which uniquely 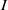$I$-clean rings coincide with uniquely clean rings. Further we prove that a ring 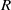$R$ is uniquely nil-clean if and only if (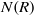$N(R)$ is an ideal of 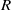$R$ and 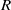$R$ is uniquely 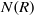$N(R)$-clean) if and only if 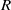$R$ is both uniquely clean and nil-clean if and only if (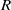$R$ is an abelian exchange ring with 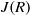$J(R)$ nil and every quasiregular element is uniquely clean). We also show that 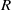$R$ is a uniquely clean ring such that every prime ideal of 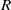$R$ is maximal if and only if 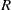$R$ is uniquely nil-clean ring and 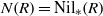$N(R)= {\mathrm{Nil} }_{\ast } (R)$.