Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T15:30:32.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of solutions of improperly posed problems for singular ultrahyperbolic equations

Published online by Cambridge University Press:  09 April 2009

Eutiquio C. Young
Eutiquio C. Young
Affiliation:
Florida State University, Tallahassee, Florida, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1], Owen gave sufficient conditions for the uniqueness of certain mixed problems having elliptic and hyperbolic nature for the ultrahyperbolic equation. Recently, Diaz and Young [2] has obtained necessary and sufficient conditions for the uniqueness of solutions of the Dirichlet and Neumann problems involving the more general ultrahyperbolic equation 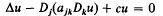The purpose of this paper is to present corresponding uniqueness conditions for the Dirichlet and Neumann problems for the singular ultrahyperbolic equation 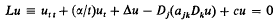for all values of the parameter, α −∞ > α > ∞. The symbol Δ denotes the Laplace operator in the variables x1, …, xm, Dj indicates partial differentiation with respect to the variable yj (1 ≧ J ≧ n), and the summation convention is adopted for repeated indices including (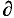iu2), where 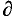denotes differentiation with respect to the variable xi.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 18 , Issue 1 , August 1974 , pp. 97 - 103
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Owens, O. G., ‘Uniqueness of solutions of ultrahyperbolic partial differential equations’, Amer. J. Math. 69 (1947), 184–188.CrossRefGoogle Scholar
[2]Diaz, J. B. and Young, E. C., ‘Uniqueness of solutions of certain boundary value problems for ultrahyperbolic equations’, Proc. Amer. Math. Soc. 29 (1971), 569–574.CrossRefGoogle Scholar
[3]Dunninger, D. R. and Zachmanoglou, E. C., ‘The condition for uniqueness of solutions of the Dirichlet problem for the wave equation in coordinate rectangles’, J. Math. Anal. Appl. 20 (1967), 17–21.CrossRefGoogle Scholar
[4]Dunninger, D. R. and Zachmanoglou, E. C., ‘The condition for uniqueness of the Dirichlet problem for hyperbolic equations in cylindrical domains’, J. Math. Mech. 18 (1969), 763–766.Google Scholar
[5]Sigillito, V. G., ‘On the uniqueness of solutions of certain improperly posed problems’, Proc. Amer. Math. Soc. 24 (1970), 828–831.Google Scholar
[6]Young, E. C., ‘Uniqueness theorems for certain improperly posed problems’, Bull. Amer. Math. Soc. 77 (1971), 253–256.CrossRefGoogle Scholar
[7]Fox, D. W., ‘The solution and Huygen's principle for a singular Cauchy problem’, J. Math. Mech. 8 (1959), 197–220.Google Scholar