Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T09:26:45.219Z Has data issue: false hasContentIssue false
  • English
  • Français

The uniqueness of bounded or measurable solutions of some functional equations

Published online by Cambridge University Press:  09 April 2009

T. D. Howroyd
T. D. Howroyd
Affiliation:
University of Melbourne Victoria, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we are concerned with the uniqueness of solutions of functional equations of the form 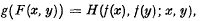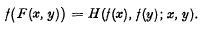Some conditions for (1) or (2) to have at most one real continuous solution f which satisfies two given initial conditions are contained in [2], [3], [4] and [7]. Conditions sufficient for the equation 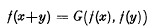to determine at most one continuous solution f with values in a Banach algebra are contained in [5]. It is well known (see [1] ch. 2) that one initial condition suffices for Cauchy's equation 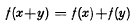or two for Jensen's equation 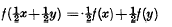to uniquely determine a real solution f which is bounded on an interval or majorized on a set of positive measure by a measurable function. We place conditions on F and H so that similar statements can be made about solutions of (1) or (2). The corresponding results for solutions which are functions of many real variables follow as for Cauchy's and Jensen's equations (see [1] ch. 5).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 2 , May 1970 , pp. 186 - 190
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Aczél, J., Lectures on Functional Equations and Their Applications, (Academic Press, New York, 1966).Google Scholar
[2]Aczél, J., ‘Ein Eindeutigkeitssatz in der Theorie der Funktionalgleichungen und einige ihrer Anwendungen’, Acta Math. Acad. Sci. Hung. 15 (1964), 355–362.CrossRefGoogle Scholar
[3]Aczél, J., ‘Ailgemeine Methoden und Eindeutigkeitssatze in der Theorie der Funktionalgleichungen’, Jber. Deutsch. Math.-Verein. 67 (1965), 133–142.Google Scholar
[4]Aczél, J. and Hosszu, M., ‘Further uniqueness theorems for functional equations’, Acta Math. Acad. Sci. Hung. 16 (1965), 51–55.CrossRefGoogle Scholar
[5]Dunford, N. and Hille, E., ‘The differentiability and uniqueness of continuous solutions of addition formulas’, Bull. Amer. Math. Soc. 53 (1947), 799–805.CrossRefGoogle Scholar
[6]Eggleston, H. G., Convexity (Cambridge University Press, Cambridge, 1958).CrossRefGoogle Scholar
[7]Howroyd, T. D., ‘Some Uniqueness Theorems for Functional Equations’, J. Australian Math. Soc. 9 (1969), 176–179.CrossRefGoogle Scholar