Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T09:22:50.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform O-estimates of certain error functions connected with k-free integers

Published online by Cambridge University Press:  09 April 2009

D. Suryanarayana
D. Suryanarayana
Affiliation:
Department of MathematicsAndhra University Waltair, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be a fixed integer ≧ 2. A positive integer m is called k-free if m is not divisible by the k'th power of any integer > 1. Let qk(m) be the characteristic function of the set of k-free integers; that is, qk(m) = 1 or 0 according as m is k-free or not. It can be easily shown that 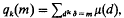where μ(n) is the Mobius function. Let x ≧ 1 denote a real variable and n be a positive integer. Let Qk(x, n) and 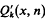be the number and the sum of the reciprocals of the k-free integers ≦ x which are prime to n respectively.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 2 , May 1970 , pp. 242 - 250
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Bergmann, G. M., ‘Solution of the problem 5091’, Amer. Math. Monthly 71 (1964), 334–335.Google Scholar
[2]Cohen, E., ‘Arithmetical functions associated with the unitary divisors of an integer’, Math. Zeit. 74 (1960), 66–80.CrossRefGoogle Scholar
[3]Cohen, E., ‘Remark on a set of integers’, Acta Sci. Math. (Szeged) 25 (1964), 179–180.Google Scholar
[4]Dickson, L. E., History of the Theory of numbers, Vol. I (Chelsea reprint, New York, 1952).Google Scholar
[5]Landau, E., Handbuch der Lehre von der Verteilung der Primzahlen (Leipzig, 1909; Chelsea reprint, 1953), p. 594.Google Scholar
[6]Robinson, R. L., ‘An estimate for the enumerative functions of certain sets of integers’, Proc. Amer. Math. Soc. 17 (1966), 232–237.CrossRefGoogle Scholar
[7]Suryanarayana, D., ‘The number of k-ary divisors of an integer’, Monatsh. Math. 72 (1968), 445–450.CrossRefGoogle Scholar
[8]Suryanarayana, D., ‘The greatest divisor of n which is prime to k’, Maths Student 36 (1968), 171–181.Google Scholar