Unbiased distinguishing of translation families and integrability with respect to a convolution of measures

Extract

Let M₁ and M₂ be two sets of probability measures defined on Rⁿ. Ameasurable R¹ valued function h (l ≧1) is said to distinguish M₁from M₂unbiasedly if there are numbers or vectors I₁ and I₂ (I₁≠I₂) such that ∫_Rⁿh(x)m(dx) = I_i if m is in M_i (i = 1, 2). Here we shall be concerned with the case where M₁ and M₂ are translation families, in that all of the elements of M_i are translates of a single measure m_i. This means that if, for any t in R_n, m^t_t is the measure defined by 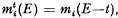, where E−t {x−t: x ∈ E}, then M_i = 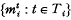, where T is a subset of R_n. If M₁ and M₂ are of this type, we will investigate the conditions under which there does not exist a function to distinguishing M₁ from M₂ unbiasedly. A case of special interest arises if m₂(E) = m₁(BE) = m₁ 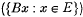with B a non-degenerate n × n matrix, and particularly a nonzero multiple (scale parameter) of the identity matrix, cf. [1], [2]. For simplicity, take l = 1.