Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T19:20:30.749Z Has data issue: false hasContentIssue false
  • English
  • Français

β-transformation, invariant measure and uniform distribution

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Measure-theoretic ergodic theory

Published online by Cambridge University Press:  09 April 2009

Gavin Brown  and
Qinghe Yin
Gavin Brown
Affiliation:
Vice-Chancellor, The University of Sydney, NSW 2006, Australia
Qinghe Yin
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW 2006, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Tβ be the β-transformation on [0, 1). When β is an integer Tβ is ergodic with respect to Lebesgue measure and almost all orbits {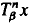} are uniformly distributed. Here we consider the non-integer case, determine when Tα, Tβ have the same invariant measure and when (appropriately normalised) orbits are uniformly distributed.

Keywords

β-transformationinvariant measureuniform distribution

MSC classification

Secondary: 28D05: Measure-preserving transformations 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 11K06: General theory of distribution modulo $1$
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 66 , Issue 3 , June 1999 , pp. 418 - 428
Copyright
Copyright © Australian Mathematical Society 1999

References

[1]Brown, G. and Yin, Q., ‘β-transformation, natural extension and invariant measure’, Ergodic Theory Dynamical Systems (to appear).Google Scholar
[2]Cornfeld, I. P., Fomin, S. V. and Sinai, Ya. G., Ergodic theory (Springer, New York, 1982).CrossRefGoogle Scholar
[3]Ito, S. and Takahashi, Y., ‘Markov subshifts and realization of β-expansions’, J. Math. Soc. Japan 26 (1974), 33–55.CrossRefGoogle Scholar
[4]Parry, W., ‘On the β-expansion of real numbers’, Acta Math. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
[5]Rényi, A., ‘Represenations of real numbers and their ergodic properties’, Acta Math. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
[6]Schweiger, F., ‘Metrische sätze über Oppenheimentwicklungen’, J. Reine Angew. Math. 254 (1972), 152–159.Google Scholar
[7]Schweiger, F., Ergodic theory of fibred systems and metric number theory (Oxford University Press, Oxford, 1995).Google Scholar
[8]Takahashi, Y., ‘Isomorphisms of β-automorphisms to Markov automorphisms’, Osaka J. Math. 10 (1973), 157–184.Google Scholar