Article contents
Toeplitz operators on certain weakly pseudoconvex domains
Published online by Cambridge University Press: 09 April 2009
Abstract
Let Ω be the weakly pseudoconvex domain
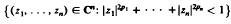
and let ∂Ω be its boundary. If ϕ ∈ L∞ (∂Ω), we denote by Tϕ, the Toephtz operator with symbol ϕ acting on the Hardy space H2(∂Ω), and by J(∂Ω) the C*-subalgebra of B(H2(∂Ω)) generated by the Toeplitz operators with continuous symbol. Our main theorem asserts that J(∂Ω) contains the ideal K of all compact operators on H2(∂Ω), and that the symbol map ϕ→Tϕ induces an isomorphism of C(∂Ω) onto the quotient C*-algebra ℑ(∂Ω)/K. Similar results have been established before for other domains, and in particular when Ω is strongly pseudoconvex. The main interest of our results lies in their proofs: ours are elementary, whereas those used in the strongly pseudoconvex case depend heavily on the theory of the tangential Cauchy-Riemann operator.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1981
References
- 9
- Cited by


