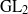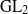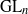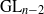Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kim, Sangjib
2018.
A presentation of the double Pieri algebra.
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 2,
p.
368.
Lauret, Emilio A.
and
Rossi Bertone, Fiorela
2018.
On the SO(n + 3) to SO(n) branching multiplicity space.
Comptes Rendus. Mathématique,
Vol. 356,
Issue. 11-12,
p.
1112.